VẤN ĐỀ 2: ĐIỆN TRƯỜNG, CƯỜNG ĐỘ ĐIỆN TRƯỜNG.
LÝ THUYẾT TRỌNG TÂM
– Điện trường là môi trường bao quanh điện tích và tác dụng lực điện lên điện tích khác đặt trong nó.
– Cường độ điện trường: đặc trưng cho độ mạnh yếu của điện trường về phương diện tác dụng lực lên một điện tích q đặt trong nó:
$\overrightarrow{E}=\frac{\overrightarrow{F}}{q}\Rightarrow \left\{ \begin{array}{} q>0:\overrightarrow{F}\uparrow \uparrow \overrightarrow{E} \\ {} q<0:\overrightarrow{F}\uparrow \downarrow \overrightarrow{E} \\ \end{array} \right.$
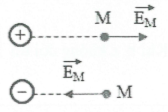
Với điện tích điểm ${{E}_{M}}=k\frac{\left| Q \right|}{\varepsilon r_{M}^{2}}$ và có chiều đi ra nếu Q dương, chiều đi vào nếu Q âm (hình vẽ).
– Nguyên lí chồng chất điện trường: $\overrightarrow{{{E}_{M}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}+\overrightarrow{{{E}_{3}}}+…$
– Đưòng sức điện là đường mà tiếp tuyển tại mỗi điểm của nó là giá của vectơ cđđt tại điểm đó.
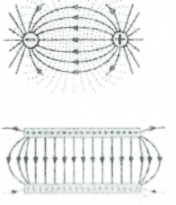
+ Đường sức điện là đường không khép kín, đi ra từ điện tích (+) và kết thúc ở điện tích (-) hoặc vô tận
+ Qua mỗi điểm trong điện trường chỉ duy nhất có một đường sức (các đường sức ko cắt nhau).
+ Nơi nào điện trường mạnh đường sức dày và ngược lại.
– Điện trường đều: có vectơ cường độ điện trường tại mọi điểm đều có cùng phương, chiều và độ lớn; đường sức điện là những đường thẳng song song khép kín, cách đều.
CÁC DẠNG BÀI TẬP
DẠNG 1: CƯỜNG ĐỘ ĐIỆN TRƯỜNG. LỰC TÁC DỤNG LÊN ĐIỆN TÍCH ĐẶT TRONG ĐIỆN TRƯỜNG.
PHƯƠNG PHÁP GIẢI
– Cường độ điện trường do một điện tích điểm gây ra:
+) $\overrightarrow{{{E}_{M}}}$ có phương nằm trên đường thẳng nối điện tích điếm Q với điểm M, chiều đi ra nếu Q dương, có chiều đi vào nếu Q âm.
+) Độ lớn ${{E}_{M}}=k\frac{\left| Q \right|}{\varepsilon r_{M}^{2}}$
Þ Khi Q, e không đổi ta có: $E=\frac{1}{{{r}^{2}}}\Leftrightarrow r=\frac{1}{\sqrt{E}}\Rightarrow \frac{{{E}_{M}}}{{{E}_{N}}}=\frac{r_{N}^{2}}{r_{M}^{2}}$
– Lực do điện trường $\overrightarrow{E}$ tác dụng lên điện tích q đặt trong nó:
+) Biểu thức: $\overrightarrow{F}=q.\overrightarrow{E}\Rightarrow \left\{ \begin{array}{} q>0\Rightarrow \overrightarrow{F}\uparrow \uparrow \overrightarrow{E} \\ {} q<0\Rightarrow \overrightarrow{F}\uparrow \downarrow \overrightarrow{E} \\ \end{array} \right.$
+) Độ lớn: $F=\left| q \right|E$
BÀI TẬP LUYỆN TẬP DẠNG 1
|
Bài tập 1: Xác định vectơ cường độ điện trường tại M trong không khí cách điện tích điểm$q={{2.10}^{-8}}C$ một khoảng 3 cm. |
Lời giải chi tiết
Ta có q > 0 nên vecto E có gốc đặt tại M, chiều đi ra xa điện tích q
Độ lớn $E=k\frac{\left| q \right|}{\varepsilon {{r}^{2}}}={{9.10}^{9}}.\frac{{{2.10}^{-8}}}{1.0,{{03}^{2}}}={{2.10}^{5}}V/m$
|
Bài tập 2: Một điện tích q trong nước $\left( \varepsilon =81 \right)$gây ra tại điểm M cách điện tích một khoảng r = 26 cm một điện trường $E=1,{{5.10}^{4}}V/m.$ Hỏi tại điểm N cách điện tích q một khoảng r = 17 cm có cường độ điện trường bằng bao nhiêu? |
Lời giải chi tiết
Khi q, e không đổi thì $E=\frac{1}{{{r}^{2}}}$ nên $\frac{{{E}_{M}}}{{{E}_{N}}}={{\left( \frac{{{r}_{N}}}{{{r}_{M}}} \right)}^{2}}\Rightarrow \frac{1,5}{{{E}_{M}}}={{\left( \frac{17}{26} \right)}^{2}}\Rightarrow {{E}_{M}}\approx 3,{{5.10}^{4}}V/m$
|
Bài tập 3: Cho hai điểm A và B cùng nằm trên một đường sức điện do điện tích q < 0 gây ra. Biết độ lớn của cường độ điện trường tại A là 49 V/m, tại B là 16 V/m. a) Xác định cường độ điện trường tại trung điểm M của AB. b) Nếu đặt tại M một điện tích ${{q}_{0}}={{2.10}^{-2}}C$thì lực điện tác dụng lên nó có độ lớn là bao nhiêu? Xác định phương chiều của lực này. |
Lời giải chi tiết
a) Ta có: $2{{r}_{M}}={{r}_{A}}+{{r}_{B}}\left( 1 \right)$
Mà $E=\frac{1}{{{r}^{2}}}\Rightarrow r=\frac{1}{\sqrt{E}}$ nên (1) $\Leftrightarrow \frac{2}{\sqrt{{{E}_{M}}}}=\frac{1}{\sqrt{{{E}_{A}}}}+\frac{1}{\sqrt{{{E}_{B}}}}\Leftrightarrow \frac{2}{\sqrt{{{E}_{M}}}}=\frac{1}{7}+\frac{1}{4}\Rightarrow {{E}_{M}}\approx 26V/m$
Do q < 0 Þ E hướng vào điện tích q
b) $F={{q}_{0}}.{{E}_{M}}={{2.10}^{-2}}.26=0,52N;{{q}_{0}}>0\Rightarrow F$ cùng chiều với E nên lực điện này là lực hút
DẠNG 2: CƯỜNG ĐỘ ĐIỆN TRƯỜNG DO HỆ NHIỀU ĐIỆN TÍCH ĐIỂM GÂY RA
PHƯƠNG PHÁP GIẢI
Áp dụng nguyên lý chồng chất điện trường:
– Xác định phương, chiều, độ lớn của từng vectơ cường độ điện trường do từng điện tích gây ra.
– Vẽ vectơ cường độ điện trường tổng hợp (quy tắc hình bình hành).
– Xác định độ lớn của cường độ điện trường tổng hợp từ hình vẽ.
Khi xác định tổng của hai vectơ cần lưu ý các trường hợp đặc biệt: $\uparrow \uparrow ,\downarrow \downarrow ,\bot $ , tam giác vuông, tam giác đều,… Nếu không xảy ra các trường họp đặt biệt thì có thể tính độ dài của vectơ bằng định lý hàm cosin: ${{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc.cosA$
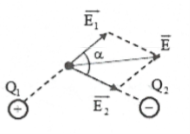
– Xét trường hợp tại điểm M trong vùng điện trường của 2 điện tích: $\overrightarrow{{{E}_{M}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}$
+) $\overrightarrow{{{E}_{1}}}\uparrow \uparrow \overrightarrow{{{E}_{2}}}\Rightarrow {{E}_{M}}={{E}_{1}}+{{E}_{2}}$
+) $\overrightarrow{{{E}_{1}}}\uparrow \downarrow \overrightarrow{{{E}_{2}}}\Rightarrow {{E}_{M}}={{E}_{1}}-{{E}_{2}}$
+) $\overrightarrow{{{E}_{1}}}\bot \overrightarrow{{{E}_{2}}}\Rightarrow {{E}_{M}}=\sqrt{E_{1}^{2}+E_{2}^{2}}$
+) $\left( \overrightarrow{{{E}_{1}}},\overrightarrow{{{E}_{2}}} \right)=\alpha \Rightarrow {{E}_{M}}=\sqrt{E_{1}^{2}+E_{2}^{2}+2{{E}_{1}}{{E}_{2}}\cos \alpha }$
Nếu ${{E}_{1}}={{E}_{2}}\Rightarrow E=2{{E}_{1}}\cos \frac{\alpha }{2}$
BÀI TẬP LUYỆN TẬP DẠNG 2
|
Bài tập 4: Có 2 điện tích ${{q}_{1}}=0,5nC,{{q}_{2}}=-0,5nC$lần lượt đặt tại hai điểm A, B cách nhau một đoạn a = 6 cm trong không khí. Hãy xác định cường độ điện trường $\overrightarrow{E}$ tại điểm M trong các trường hợp sau: a) Điểm M là trung điểm của AB. b) Điểm M cách A đoạn 6 cm, cách B đoạn 12 cm. |
Lời giải chi tiết
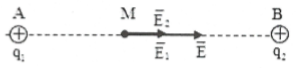
a) $\left\{ \begin{array}{} {{r}_{1}}={{r}_{2}}=r \\ {} \left| {{q}_{1}} \right|=\left| {{q}_{2}} \right|=q \\ \end{array} \right.\Rightarrow {{E}_{1}}={{E}_{2}}=k\frac{\left| q \right|}{r_{M}^{2}}=5000V/m$
Điện trường tổng hợp gây ra tại M: $\overrightarrow{E}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}$
Vì $\overrightarrow{{{E}_{1}}},\overrightarrow{{{E}_{2}}}$ cùng chiều nên $E={{E}_{1}}+{{E}_{2}}=10000V/m$
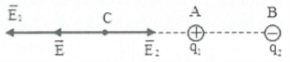
b) Ta có: $\left\{ \begin{array}{} {{E}_{1}}=k\frac{\left| {{q}_{1}} \right|}{r_{1}^{2}}={{9.10}^{9}}.\frac{0,{{5.0}^{-9}}}{0,{{06}^{2}}}=1250V/m \\ {} {{E}_{2}}=k\frac{\left| {{q}_{1}} \right|}{r_{2}^{2}}={{9.10}^{9}}.\frac{0,{{5.0}^{-9}}}{0,{{12}^{2}}}=312,5V/m \\ \end{array} \right.$
Điện trường tổng hợp gây ra tại M: $\overrightarrow{E}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}$
Vì $\overrightarrow{{{E}_{1}}},\overrightarrow{{{E}_{2}}}$ ngược chiều nên: $E={{E}_{1}}-{{E}_{2}}=937,5V/m$
|
Bài tập 5: Tại 3 đỉnh A, B, C của hình vuông ABCD cạnh a đặt 3 điện tích q giống nhau (q > 0). Tính E tại: a) Tâm O hình vuông. b) Đỉnh D. |
Lời giải chi tiết
a) vì ${{q}_{1}}={{q}_{2}}={{q}_{3}}=q;{{r}_{1}}={{r}_{2}}={{r}_{3}}=\frac{a\sqrt{2}}{2}$ nên ${{E}_{1}}={{E}_{2}}={{E}_{3}}$
Điện trường tại O: $\overrightarrow{{{E}_{0}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}+\overrightarrow{{{E}_{3}}}=\overrightarrow{{{E}_{13}}}+\overrightarrow{{{E}_{2}}}$
Vì $\overrightarrow{{{E}_{1}}},\overrightarrow{{{E}_{3}}}$ ngược chiều nên $\overrightarrow{{{E}_{13}}}=0$ nên ${{E}_{0}}={{E}_{2}}=k\frac{q}{{{\left( \frac{a\sqrt{2}}{2} \right)}^{2}}}=\frac{2kq}{{{a}^{2}}}$
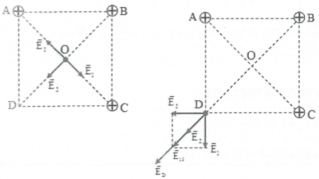
b) $\overrightarrow{{{E}_{D}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}+\overrightarrow{{{E}_{3}}}=\overrightarrow{{{E}_{13}}}+\overrightarrow{{{E}_{2}}}$
Vì ${{r}_{1}}={{r}_{3}};{{r}_{2}}=a\sqrt{2}$ nên ${{E}_{1}}={{E}_{3}}=k\frac{q}{{{a}^{2}}};{{E}_{2}}=k\frac{q}{2{{a}^{2}}}$
Mặt khác, vì $\overrightarrow{{{E}_{1}}},\overrightarrow{{{E}_{3}}}$ vuông góc nhau nên ${{E}_{13}}={{E}_{1}}\sqrt{2}=k\frac{\sqrt{2}q}{{{a}^{2}}}$
Vì $\overrightarrow{{{E}_{13}}},\overrightarrow{{{E}_{2}}}$ cùng chiều nên ${{E}_{D}}={{E}_{13}}+{{E}_{2}}\Rightarrow {{E}_{D}}=k\frac{\sqrt{2}q}{{{a}^{2}}}+k\frac{q}{2{{a}^{2}}}=\left( \sqrt{2}+\frac{1}{2} \right)\frac{kq}{{{a}^{2}}}$
|
Bài tập 6: Hai điện tích ${{q}_{1}}={{q}_{2}}=6,{{4.10}^{-10}}C$ , đặt tại 2 đỉnh B và C của một tam giác đều ABC có cạnh bằng 8 cm, trong không khí. a) Hãy tính cường độ điện trường tại đỉnh A của tam giác ? b) Gọi M là điểm nằm trên đường trung trực của BC, x là khoảng cách từ M đến BC. Xác định x để cường độ điện trường tổng hợp tại M lớn nhất. Tính giá trị đó. |
Lời giải chi tiết
a) Gọi $\overrightarrow{{{E}_{1}}},\overrightarrow{{{E}_{2}}}$ lần lượt là cường độ điện trường do điện tích ${{q}_{1}},{{q}_{2}}$ gây ra tại M. Độ lớn 2 điện tích bằng nhau và điểm M cách đều 2 điện tích nên:
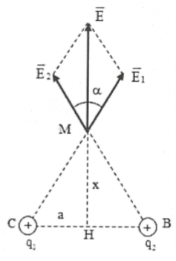
${{E}_{1}}={{E}_{2}}=k\frac{\left| q \right|}{{{r}^{2}}}={{9.10}^{9}}.\frac{6,{{4.10}^{-10}}}{0,{{08}^{2}}}=900V/m$
Cường độ điện trường tổng hợp: $\overrightarrow{E}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}$
$\Rightarrow E=\sqrt{E_{1}^{2}+E_{2}^{2}+2{{E}_{1}}{{E}_{2}}\cos 60{}^\circ }\Leftrightarrow E={{E}_{1}}\sqrt{3}=900\sqrt{3}\,V/m$
b) Độ lớn 2 điện tích bằng nhau và M cách đều 2 điện tích nên:
${{E}_{1}}={{E}_{2}}=k\frac{\left| q \right|}{{{r}^{2}}}=k\frac{\left| q \right|}{M{{H}^{2}}+H{{C}^{2}}}=k\frac{q}{{{x}^{2}}+{{a}^{2}}}$
Do ${{E}_{1}}={{E}_{2}}$ nên hình $M{{E}_{1}}E{{E}_{2}}$ là hình thoi nên:
$ME=2.M{{E}_{1}}\cos \alpha \Leftrightarrow E=2.{{E}_{1}}\cos \alpha =2k\frac{q}{{{x}^{2}}+{{a}^{2}}}\frac{x}{\sqrt{{{x}^{2}}+{{a}^{2}}}}$
$\Leftrightarrow E=\frac{2kqx}{\sqrt{{{\left( {{x}^{2}}+{{a}^{2}} \right)}^{3}}}}=\frac{2kqx}{\sqrt{{{\left( \frac{{{a}^{2}}}{2}+\frac{{{a}^{2}}}{2}+{{x}^{2}} \right)}^{3}}}}$
Theo Cô-si: $\frac{{{a}^{2}}}{2}+\frac{{{a}^{2}}}{2}+{{x}^{2}}\ge 3\sqrt[3]{\frac{{{a}^{2}}}{2}.\frac{{{a}^{2}}}{2}.{{x}^{2}}}\Rightarrow {{\left( \frac{{{a}^{2}}}{2}+\frac{{{a}^{2}}}{2}+{{x}^{2}} \right)}^{3}}\ge \frac{27}{4}{{a}^{4}}{{x}^{2}}$
Vậy ${{E}_{\max }}=\frac{2kq}{\frac{3\sqrt{3}}{2}{{a}^{2}}}=2771,28V/m$ khi $\frac{{{a}^{2}}}{2}={{x}^{2}}\Rightarrow x=\frac{a\sqrt{2}}{2}=2\sqrt{2}cm$
DẠNG 3: ĐIỆN TRƯỜNG TRIỆT TIÊU
PHƯƠNG PHÁP GIẢI
– Nếu $\overrightarrow{{{E}_{M}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}=\overrightarrow{0}$ thì $\overrightarrow{{{E}_{1}}}=-\overrightarrow{{{E}_{2}}}\Rightarrow \left\{ \begin{array}{} \overrightarrow{{{E}_{1}}}\uparrow \downarrow \overrightarrow{{{E}_{2}}} \\ {} {{E}_{1}}={{E}_{2}} \\ \end{array} \right.$
– Nếu $\overrightarrow{{{E}_{M}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}+\overrightarrow{{{E}_{3}}}=\overrightarrow{0}\Rightarrow \overrightarrow{{{E}_{3}}}=-\left( \overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}} \right)…$
BÀI TẬP LUYỆN TẬP DẠNG 3
|
Bài tập 7: Tại hai điểm A, B cách nhau 15 cm trong không khí đặt${{q}_{1}}=-{{12.10}^{-6}}C,{{q}_{2}}=2,{{5.10}^{-6}}C$ . Tìm điểm M mà tại đó cường độ điện trường tổng hợp do hai điện tích này gây ra bằng 0 |
Lời giải chi tiết
Gọi $\overrightarrow{{{E}_{1}}},\overrightarrow{{{E}_{2}}}$ là cường độ điện trường do ${{q}_{1}},{{q}_{2}}$ gây ra tại M thì cường độ điện trường tổng hợp do ${{q}_{1}},{{q}_{2}}$ gây ra tại M là $\overrightarrow{{{E}_{M}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}=\overrightarrow{0}\Rightarrow \overrightarrow{{{E}_{1}}}=-\overrightarrow{{{E}_{2}}}\Rightarrow \left\{ \begin{array}{} \overrightarrow{{{E}_{1}}}\uparrow \downarrow \overrightarrow{{{E}_{2}}} \\ {} {{E}_{1}}={{E}_{2}} \\ \end{array} \right.$
Để thỏa mãn các điều kiện trên thì M phải nằm trên đường thẳng nổi AB; nằm ngoài đoạn thẳng AB và gần ${{q}_{2}}$ hơn.
Với ${{E}_{1}}={{E}_{2}}$ thì ${{9.10}^{9}}\frac{\left| {{q}_{1}} \right|}{A{{M}^{2}}}={{9.10}^{9}}\frac{\left| {{q}_{1}} \right|}{{{\left( AM-AB \right)}^{2}}}\Rightarrow \frac{AM}{AM-AB}=\sqrt{\left| \frac{{{q}_{1}}}{{{q}_{2}}} \right|}=2\Rightarrow AM=2AB=30cm$
Vậy M nằm cách A 30 cm và cách B 15 cm; ngoài ra còn có các điểm ở cách rất xa điểm đặt các điện tích ${{q}_{1}},{{q}_{2}}$ cũng có cường độ điện trường bằng 0 vì ở đó cường độ điện trường do các điện tích ${{q}_{1}},{{q}_{2}}$ gây ra đều » 0.
|
Bài tập 8: Tại hai điểm A, B cách nhau 20 cm trong không khí đặt${{q}_{1}}=-{{9.10}^{-6}}C,{{q}_{2}}=-{{4.10}^{-6}}C$ . Tìm điểm M mà tại đó cường độ điện trường tổng hợp do hai điện tích này gây ra bằng 0. |
Lời giải chi tiết
Gọi $\overrightarrow{{{E}_{1}}},\overrightarrow{{{E}_{2}}}$ là cường độ điện trường do ${{q}_{1}},{{q}_{2}}$ gây ra tại M thì cường độ điện trường tổng hợp do ${{q}_{1}},{{q}_{2}}$ gây ra tại M là
$\overrightarrow{{{E}_{M}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}=\overrightarrow{0}\Rightarrow \overrightarrow{{{E}_{1}}}=-\overrightarrow{{{E}_{2}}}\Rightarrow \left\{ \begin{array}{} \overrightarrow{{{E}_{1}}}\uparrow \downarrow \overrightarrow{{{E}_{2}}} \\ {} {{E}_{1}}={{E}_{2}} \\ \end{array} \right.$
Để thỏa mãn các điều kiện trên thì M phải nằm trên đường thẳng nổi AB; nằm trong đoạn thẳng AB
Với ${{E}_{1}}={{E}_{2}}$ thì $\frac{AM}{AM-AB}=\sqrt{\left| \frac{{{q}_{1}}}{{{q}_{2}}} \right|}=\frac{3}{2}\Rightarrow AM=\frac{3AB}{5}=12cm$
Vậy M nằm cách A 12 cm và cách B 8 cm; ngoài ra còn có các điểm ở cách rất xa điểm đặt các điện tích ${{q}_{1}},{{q}_{2}}$cũng có cường độ điện trường bằng 0 vì ở đó cường độ điện trường do các điện tích ${{q}_{1}},{{q}_{2}}$gây ra đều » 0.
|
Bài tập 9: Cho hình vuông ABCD, tại A và C đặt các điện tích${{q}_{1}}={{q}_{3}}=q$ . Hỏi phải đặt tại B một điện tích bao nhiêu để cường độ điện trường tại D bằng 0. |
Lời giải chi tiết
$\overrightarrow{{{E}_{1}}},\overrightarrow{{{E}_{2}}},\overrightarrow{{{E}_{3}}}$ là cường độ điện trường do ${{q}_{1}},{{q}_{3}},{{q}_{2}}$gây ra tại D.
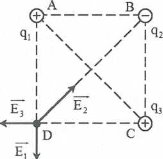
Cường độ diện trường tổng họp tại đỉnh D của hình vuông:
$\overrightarrow{{{E}_{D}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}+\overrightarrow{{{E}_{3}}}$
Đê cường độ điện trường tại D bị triệt tiêu thì $\overrightarrow{{{E}_{D}}}=0$
Vì ${{q}_{1}}={{q}_{3}}$ và $AD=CD$ nên ${{E}_{1}}={{E}_{3}}$ và cường độ điện trường tổng hợp:
$\overrightarrow{{{E}_{13}}}=\sqrt{2}{{E}_{1}}=\sqrt{2}k\frac{\left| q \right|}{{{a}^{2}}}$
Để $\overrightarrow{{{E}_{D}}}=0$ thì $\left\{ \begin{array}{} \overrightarrow{{{E}_{2}}}\uparrow \downarrow \overrightarrow{{{E}_{13}}} \\ {} {{E}_{2}}={{E}_{13}} \\ \end{array} \right.\Rightarrow k\frac{\left| {{q}_{2}} \right|}{{{\left( a\sqrt{2} \right)}^{2}}}=\sqrt{2}k\frac{\left| q \right|}{{{\left( a \right)}^{2}}}\Rightarrow \left| {{q}_{2}} \right|=2\sqrt{2}\left| q \right|$
Vì $\overrightarrow{{{E}_{2}}}\uparrow \downarrow \overrightarrow{{{E}_{13}}}\Rightarrow {{q}_{2}}=-2\sqrt{2}q$
DẠNG 4: ĐIỀU KIỆN CÂN BẰNG CỦA VẬT MANG ĐIỆN ĐẶT TRONG ĐIỆN TRƯỜNG ĐỀU
PHƯƠNG PHÁP GIẢI
+) Xác định các lực tác dụng lên vật.
+) Biểu diễn các lực tác dụng lên vật.
+) Sử dụng điều kiện cân bằng $\overrightarrow{{{F}_{hl}}}=0$ , tìm các đại lượng cần tìm.
Các lực thường gặp là: lực điện $\overrightarrow{F}=q\overrightarrow{E}$ , trọng lực $\overrightarrow{P}=m\overrightarrow{g}$ và lực đẩy Acsimet $\overrightarrow{{{F}_{A}}}=-\rho V\overrightarrow{g}$
BÀI TẬP LUYỆN TẬP DẠNG 4
|
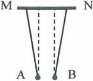
Bài tập 10: Hai quả cầu nhỏ A và B mang những điện tích lần lượt $-{{2.10}^{-9}}C$ và ${{2.10}^{-9}}C$ được treo ở đầu hai sợi dây tơ cách điện dài bằng nhau. Hai điểm treo dây M và N cách nhau 2 cm. Khi cân bằng, vị trí các dây treo có dạng như hình vẽ. Hỏi để đưa các dây treo trở về vị trí thẳng đứng người ta phải dùng một điện trường đều có hướng nào và độ lớn bao nhiêu? |
Lời giải chi tiết
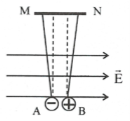
Để đưa các dây treo trở về vị trí thẳng đứng cần phải tác dụng lực điện trường ngược chiều với lực tĩnh điện và cùng độ lớn với lực tĩnh điện: F’ = F
+) Với quả cầu A: $\left| q \right|E=k\frac{{{q}^{2}}}{A{{B}^{2}}}$
$\Rightarrow E=k\frac{\left| q \right|}{A{{B}^{2}}}=k\frac{\left| q \right|}{M{{N}^{2}}}={{9.10}^{9}}.\frac{{{2.10}^{-9}}}{{{\left( {{2.10}^{-2}} \right)}^{2}}}=4,{{5.10}^{4}}V/m$
Do ${{q}_{1}}<0$ nên $\overrightarrow{E}$ ngược chiều với$\overrightarrow{F’}$ nghĩa là cùng chiều với $\overrightarrow{F}$ (hướng từ trái sáng phải)
+) Với quả cầu B: tương tự
Þ Để đưa các dây treo trở về vị trí thẳng đứng cần phải dùng một điện trường đều có hướng từ trái sang phải và có độ lớn$E=4,{{5.10}^{4}}V/m$ .
|
Bài tập 11: Một hòn bi nhỏ bằng kim loại được đặt trong dầu. Bi có thể tích V = 10 mm3, khối lượng $m={{9.10}^{-5}}kg$ . Dầu có khối lượng riêng D = 800 kg/m3. Tất cả được đặt trong một điện trường đều, E hướng thẳng đứng từ trên xuống, $E=4,{{1.10}^{5}}V/m$ . Tìm điện tích của bi để nó cân bằng lơ lủng trong dầu. Cho g = 10 m/s2. |
Lời giải chi tiết
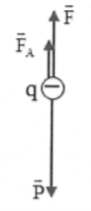
Các lực tác dụng lên hòn bi:
Trọng lực $\overrightarrow{P}=m\overrightarrow{g}$ lực đẩy Acsimet $\overrightarrow{{{F}_{A}}}=-\rho V\overrightarrow{g}$
Lực điện trường: $\overrightarrow{F}=q\overrightarrow{E}$ (hướng xuống nếu q > 0; hướng lên nếu q < 0)
Hòn bi nằm cân bằng (lơ lửng) khi: $\overrightarrow{P}+\overrightarrow{{{F}_{A}}}+\overrightarrow{F}=\overrightarrow{0}\Rightarrow \overrightarrow{P’}+\overrightarrow{F}=\overrightarrow{0}$
Vì $P>{{F}_{A}}$ nên $P’=P-{{F}_{A}}\Rightarrow \overrightarrow{F}$ phải hướng lên $\Rightarrow q<0$ và $F=P-{{F}_{A}}$
$\Rightarrow \left| q \right|E=mg-DVg\Rightarrow \left| q \right|=\frac{mg-DVg}{E}=\frac{{{9.10}^{-5}}-{{800.10}^{-8}}.10}{4,{{1.10}^{5}}}={{2.10}^{-9}}C$
Vì $q<0$ nên $q=-{{2.10}^{-9}}C$
|
Bài tập 12: Một quả cầu kim loại bán kính r = 3mm được tích điện $q={{10}^{-6}}C$ treo vào một đầu dây mảnh trong dầu. Điện trường đều trong dầu có $\overrightarrow{E}$ hướng thẳng đứng từ trên xuống. Khối lượng riêng của kim loại ${{\rho }_{1}}=8720kg/{{m}^{3}}$, của dầu ${{\rho }_{2}}=800kg/{{m}^{3}}$. Biết rằng lực căng dây cực đại bằng 1,4N. Tính E để dây không đứt. Lấy $g=10m/{{s}^{2}}$ |
Lời giải chi tiết
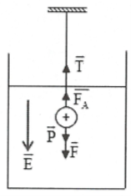
Quả cầu có cân bằng: $\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{{{F}_{A}}}+\overrightarrow{T}=0$
$\Rightarrow T=P-{{F}_{A}}+F=\frac{3}{4}\pi {{r}^{2}}g\left( {{\rho }_{1}}-{{\rho }_{2}} \right)+qE\le {{T}_{\max }}$
$\Rightarrow E\le \frac{1}{q}\left[ {{T}_{\max }}-\frac{4}{3}\pi {{r}^{3}}g\left( {{\rho }_{1}}-{{\rho }_{2}} \right) \right]=1,{{391.10}^{6}}V/m$
|
Bài tập 13: Cho hai kim loại song song, nằm ngang, nhiễm điện trái dấu. Khoảng không gian giữa 2 tấm kim loại đó chứa đầy dầu. Một quả cầu bằng sắt bán kính R = 1cm mang điện tích q nằm lơ lửng trong lớp dầu. Điện trường giữa 2 tấm kim loại là điện trường đều hướng từ trên xuống và có độ lớn 20000V/m. Hỏi độ lớn và dấu của điện tích q. Cho biết khối lượng riêng của sắt là 7800kg/m3, của dầu là 800kg/m3. Lấy $g=10m/{{s}^{2}}$ |
Lời giải chi tiết
Các lực tác dụng lên quả cầu: lực điện $\overrightarrow{F}$ , trong lực $\overrightarrow{P}$ hướng xuống và lực đẩy Acsimet $\overrightarrow{{{F}_{A}}}$ hướng lên. Điều kiện cân bằng của quả cầu: $\overrightarrow{P}+\overrightarrow{{{F}_{d}}}+\overrightarrow{{{F}_{A}}}=0$
Lại có: $\left\{ \begin{array}{} P=mg={{\rho }_{vat}}Vg={{\rho }_{vat}}\frac{4}{3}\pi {{R}^{3}}g \\ {} {{F}_{A}}={{\rho }_{mt}}Vg={{\rho }_{mt}}\frac{4}{3}\pi {{R}^{3}}g \\ \end{array} \right.$
Vì khối lượng riêng của vật lớn hơn $\Rightarrow P>{{F}_{A}}\Rightarrow {{F}_{A}}+F=P\Rightarrow F=P-{{F}_{A}}$
$\Leftrightarrow \left| q \right|E=P-{{F}_{A}}\Rightarrow \left| q \right|=\frac{P-{{F}_{A}}}{E}=\frac{\frac{4}{3}\pi {{R}^{3}}g\left( {{\rho }_{vat}}-{{\rho }_{mt}} \right)}{E}=14,{{7.10}^{-6}}C$
Vậy để vật cân bằng thì lực điện phải hướng lên, ngược hướng $\overrightarrow{E}\Rightarrow q<0\Rightarrow q=-14,{{7.10}^{-6}}C$
|
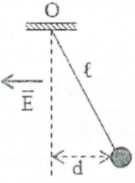
Bài tập 14: Một quả cầu khối lượng $m=4,{{5.10}^{-3}}kg$ treo vào một sợi dây dài 2m. Quả cầu nằm trong điện trường có vecto $\overrightarrow{E}$ nằm ngang, hướng sang trái như hình vẽ. Biết d = 1m, E = 2000V/m. Lấy $g=10m/{{s}^{2}}$ a) Biểu diễn các lực tác dụng lên quả cầu b) Tính điện tích của quả cầu c) tính độ lớn của lực căng dây |
Lời giải chi tiết
Các lực tác dung gồm: trọng lực $\overrightarrow{P}$ , lực điện trường $\overrightarrow{F}$ , lực căng dây $\overrightarrow{T}$
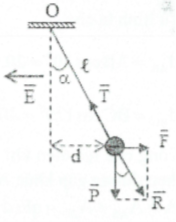
Khi quả cầu cân bằng: $\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}=0\Rightarrow \overrightarrow{R}+\overrightarrow{T}=0$
$\Rightarrow \overrightarrow{R}$ có phương sợi dây $\Rightarrow \tan \alpha =\frac{d}{\sqrt{{{\ell }^{2}}-{{d}^{2}}}}=\frac{F}{P}$
$\Leftrightarrow \frac{1}{\sqrt{{{2}^{2}}-{{1}^{2}}}}=\frac{\left| q \right|E}{mg}\Rightarrow \left| q \right|=1,{{3.10}^{-5}}C$
Do $\overrightarrow{F},\overrightarrow{E}$ ngược chiều nên q < 0 $\Rightarrow q=-1,{{3.10}^{-5}}C$
Độ lớn lực căng dây: $T=R=\frac{P}{\cos 30{}^\circ }=0,052N$