LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
1. Sóng cơ
Sóng cơ là gì?
Sóng cơ là dao động cơ lan truyền trong một môi trường.
Khi sóng cơ truyền đi chỉ có pha dao động của các phần tử vật chất lan truyền còn các phần tử vật chất thì dao động xung quanh vị trí cân bằng cố định.
Sóng ngang:
là sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng.
Trừ trường hợp sóng mặt nước, còn sóng ngang chỉ truyền được trong chất rắn.
Bài tập: sóng trên mặt nước, sóng trên sợi dây cao su.
Sóng dọc:
Là sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng.
Sóng dọc truyền được cả trong chất khí, chất lỏng và chất rắn
Bài tập: sóng âm, sóng trên lò xo.
Sóng cơ không truyền được trong chân không.
2. Các đặc trưng của một sóng hình sin
Biên độ sóng A:
Biên độ A của sóng là biên độ dao động của một phần tử của môi trường có sóng truyền qua.
Chu kì (hoặc tần số) của sóng:
Chu kì T của sóng là chu kì dao động của một phần tử của môi trường có sóng truyền qua.
Đại lượng $f=\frac{1}{T}$ gọi là tần số của sóng.
Tần số sóng luôn không đổi kể cả khi truyền từ môi trường này sang môi trường khác.
Tốc độ truyền sóng:
Tốc độ truyền sóng v là tốc độ lan truyền dao động trong môi trường.
Đối với mỗi môi trường, tốc độ truyền sóng v có một giá trị không đổi.
Tốc độ truyền sóng phụ thuộc vào 3 yếu tố:
- Nhiệt độ.
- Đặc tính đàn hồi của môi trường.
- Mật độ phân tử.
Bước sóng:
Bước sóng $\lambda $ là quãng đường mà sóng truyền được trong một chu kì.
Tacó: $\lambda =vT=\frac{v}{f}$
+) Hai phần tử cách nhau một bước sóng thì dao động đồng pha với nhau.
+) Khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng mà dao động ngược pha là $\frac{\lambda }{2}$.
+) Khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng mà dao động vuông pha là $\frac{\lambda }{4}$.
+) Khoảng cách giữa hai điểm bất kì trên phương truyền sóng mà dao động cùng pha là $k\lambda $.
+) Khoảng cách giữa hai điểm bất kì trên phương truyền sóng mà dao động ngược pha là $\left( k+0,5 \right)\lambda $.
Khi sóng truyền từ môi trường này sang môi trường khác chu kỳ (tần số) không đổi, tốc độ sóng thay đổi $\left( {{v}_{R}}>{{v}_{L}}>{{v}_{K}} \right)$ nên bước sóng thay đổi.
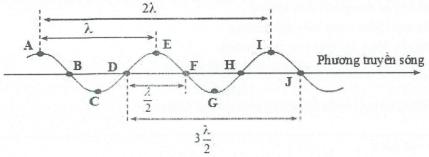
- Chú ý: Giữa 2 đỉnh (ngọn) sóng có một bước sóng.
Giữa n đỉnh (ngọn) sóng có (n – 1) bước sóng.
 3. Phương trình sóng
3. Phương trình sóng
Xét một sóng hình sin đang lan truyền trong
môi trường theo trục x, sóng này phát ra từ
một nguồn đặt tại điểm O. Chọn gốc toạ độ tại
O và chọn gốc thời gian sao cho phương trình
dao động tại O là
${{u}_{O}}=Acos\left( \omega t \right)$ Sóng hình sin tại thời điểm t
Trong đó ${{u}_{O}}$ là li độ tại O vào thời điểm t, còn t là thời gian dao động của nguồn.
Sau khoảng thời gian $\Delta t$, dao động từ O truyền đến M cách O một khoảng $x=v.\Delta t$ (v là tốc độ truyền sóng) làm cho phần tử M dao động. Do dao động tại M muộn hơn dao động tại O một khoảng thời gian $\Delta t$ nên phương trình dao động tại M là
${{u}_{M}}=Acos\left( \omega t-\Delta t \right)$
Thay $\Delta t=\frac{x}{v}$và $\lambda =vT$ ta được phương trình sóng tại M là
${{u}_{M}}=Acos\left( \omega t-\frac{x}{v} \right)=Acos\left( \frac{2\pi t}{T}-\frac{2\pi x}{\lambda } \right)\left( * \right)$
Phương trình (*) trên là phương trình sóng hình sin truyền theo trục x. Nó cho biết li độ u của phần tử có toạ độ x vào thời điểm t.
Nhận xét:
+) Từ (*) $\Rightarrow $ dao động tại M trễ pha hơn dao động tại nguồn O góc $2\pi x/\lambda $
+) Từ $\frac{2\pi x}{\lambda }\Rightarrow $x và $\lambda $ cùng đơn vị.

+) Nếu cho phương trình sóng tại I là ${{u}_{I}}\left( t \right)=a\cos \left( \omega t+\varphi \right)$. Ta có thể suy ra phương trình sóng tại P và Q (điểm đứng trước và đứng sau I):
P đứng trước: ${{u}_{P}}\left( x,t \right)=a\cos \left( \omega t+\varphi +\frac{2\pi a}{\lambda } \right)$
Q đứng sau: ${{u}_{Q}}\left( x,t \right)=a\cos \left( \omega t+\varphi -\frac{2\pi b}{\lambda } \right)$
+) Phương trình (*) là một hàm tuần hoàn vừa theo thời gian, vừa theo không gian. Thật vậy, cứ sau mỗi chu kì T thì dao động tại một điểm trên trục x lại lặp lại như trước. Và cứ cách nhau một bước sóng $\lambda $ trên trục x thì dao động tại các điểm lại giống hệt nhau (tức là cùng pha với nhau).
