VẤN ĐỀ 1: THẤU KÍNH.
LÝ THUYẾT TRỌNG TÂM
1. Các định nghĩa.
– Thấu kính là một khối chất trong suốt giới hạn bởi hai mặt cong hoặc bởi một mặt cong và một mặt phẳng.
– Phân loại:
Thấu kính hội tụ: Làm hội tụ chùm tia sáng tới Thấu kính phân kì: Làm phân kì chùm tỉa sáng tới
Phần rìa mỏng hơn phần giữa Phần giữa mỏng hơn phần rìa
– Quang tâm:
-+) Điểm O chính giữa của thấu kính mà mọi tia sáng tới truyền qua O đều truyền thẳng gọi là quang tâm của thấu kính.
-+) Đường thẳng đi qua quang tâm O và vuông góc với mặt thấu kính là trục chính của thấu kính.
-+) Các đường thẳng qua quang tâm O là trục phụ của thấu kính.
– Tiêu điểm chính:
-+) Với thấu kính hội tụ: Chùm tia ló hội tụ tại điểm F’ trên trục chính. F’ gọi là tiêu điểm chính của thấu kính hội tụ.
-+) Với thấu kính phân kì: Chùm tia ló không hội tụ thực sự mà có đường kéo dài của chúng cắt nhau tại điểm F’ trên trục chính. F’ gọi là tiêu điểm chính của thấu kính phân kì.
-+) Mỗi thấu kính mỏng có hai tiêu điểm chính nằm đối xứng nhau qua quang tâm.
-+) Một tiêu điểm gọi là tiêu điểm vật (F), tiêu điểm còn lại gọi là tiêu điểm ảnh (F’).
– Tiêu cự:
Khoảng cách f từ quang tâm đến các tiêu điểm chính gọi là tiêu cự của thấu kính: $\left| f \right|=\text{OF = OF }\!\!’\!\!\text{ }$
Qui ước: Thấu kính hội tụ thì f > 0, thấu kính phân kỳ thì f < 0.
– Độ tụ: $\text{D = }\frac{1}{\text{f}}$
+) D là độ tụ để xác định khả năng làm hội tụ chùm tia nhiều hay ít, đơn vị điôp (dp).
D > 0 thấu kính hội tụ; D < 0 thấu kính phân kỳ.
+) Công thức tính độ tụ của thấu kính:
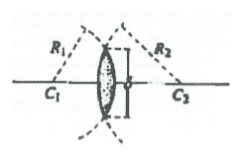$\text{D = }\frac{1}{\text{f}}=\left( \frac{\text{n}}{\text{n }\!\!’\!\!\text{ }}-1 \right)\left( \frac{1}{{{\text{R}}_{1}}}+\frac{1}{{{\text{R}}_{2}}} \right)$
Với: n là chiết suất của thấu kính.
n’ là chiết suất môi trường (không khí thì n’ = 1)
${{\text{R}}_{1}},$${{\text{R}}_{2}}$là bán kính 2 mặt của thấu kính,
qui ước: Mặt lõm R > 0, Mặt lồi R < 0, Mặt phẳng R = $\infty .$
Chú ý: Khi tính D thì đơn vị của f và R là đơn vị m.
– Trục phụ, các tiêu điểm phụ và tiêu diện:
-+) Mọi đường thẳng đi qua quang tâm O nhưng không trùng với trục chính đều gọi là trục phụ.
-+) Giao điểm của một trục phụ với tiêu diện gọi là tiêu điểm phụ ứng với trục phụ đó.
-+) Có vô số các tiêu điểm phụ, chúng đều nằm trên 1 mặt phẳng vuông góc với trục chính, tại tiêu điểm chính. Mặt phẳng đó gọi là tiêu diện của thấu kính. Mỗi thấu kính có hai tiêu diện nằm hai bên quang tâm.
2. Các tia sáng đặc biệt.
Các tia sáng khi qua thấu kính sẽ bị khúc xạ và ló ra khỏi thấu kính. Có 3 tia sáng thường gặp:
– Tia tới 1 song song với trục chính, cho tia ló (hoặc đường kéo dài) đi qua tiêu điểm ảnh.
– Tia tới 2 đi qua tiêu điểm vật, cho tia ló song song với trục chính.
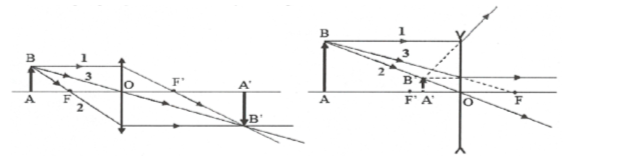– Tia tới 3 đi qua quang tâm cho tia ló truyền thẳng.
3. Ảnh cho bởi thấu kính.
Ảnh của một điểm sáng cho bởi thấu kính:
a) Điểm sáng nằm ngoài trục chính: Vẽ hai trong ba tia đặc biệt.
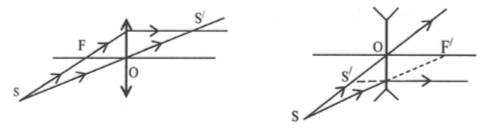
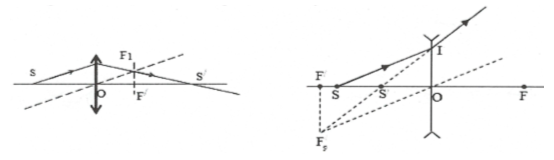b) Điểm sáng nằm trên trục chính: Dùng một tia bất kỳ và tia đi đi theo trục chính
Ảnh của một vật cho bởi thấu kính:
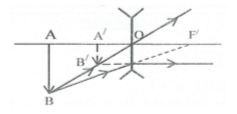
a) Với thấu kính hội tụ: Xét vật sáng là đoạn thẳng nhỏ AB vuông góc trục chính
+) Vật thật ở ngoài khoảng tiêu cự cho ảnh thật, ngược chiều với vật.
+) Vật thật ở trong khoảng tiêu cự cho ảnh ảo, cùng chiều với vật, lớn hơn vật.
+) Vật thật ở tiêu diện cho ảnh ở vô cực, không hứng được ảnh.
b) Với thấu kính phân kỳ: luôn cho ảnh ảo, cùng chiều, nhỏ hơn vật.
4. Công thức thấu kính.
– Công thức về vị trí ảnh – vật:
$\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}=\frac{1}{\text{f}}$ (công thức này dùng được cả cho thấu kính hội tụ và thấu kính phân kì)
Với:
d = OA = khoảng cách từ vật 
thấu kính: d > 0: ảnh thật (trước thấu kính)
d’ = OA’ = khoảng cách từ ảnh thấu kính
d’ > 0: ảnh thật (sau thấu kính); d’ < 0: ảnh ảo (trước thấu kính)
– Công thức về độ phóng đại của ảnh:
Độ phóng đại của ảnh là tỉ số chiều cao của ảnh và chiều cao của vật: $\text{k = }\frac{\overline{\text{A }\!\!’\!\!\text{ B }\!\!’\!\!\text{ }}}{\overline{\text{AB}}}=-\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}}$
+) k > 0: ảnh cùng chiều với vật; k < 0: ảnh ngược chiều với vật.
+) $\left| \text{k} \right|$> 1: ảnh cao hơn vật, $\left| \text{k} \right|$< 1: ảnh thấp hơn vật.
Giá trị tuyệt đối của k cho biết độ lớn tỉ đối của ảnh so với vật.
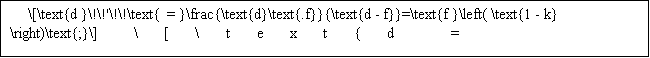Hệ quả:
Chú ý: Tỷ lệ về diện tích của vật và ảnh: $\mathbf{S}={{\left( \frac{\overline{\mathbf{A}’\mathbf{B}’}}{\mathbf{AB}} \right)}^{2}}={{\mathbf{k}}^{\mathbf{2}}}$
– Nếu vật AB tại hai vị trí cho hai ảnh khác nhau A1B1 và A2B2 thì: ${{(\text{AB)}}^{2}}=({{\text{A}}_{1}}{{\text{B}}_{1}}).({{\text{A}}_{2}}.{{\text{B}}_{2}})$
– Điều kiện để vật thật qua thấu kính cho ảnh thật là: $\text{L}\ge \text{4}\text{.f}$
– Vật AB đặt cách màn một khoảng L, có hai vị trí của thấu kính cách nhau$\ell $sao cho AB qua thấu kính cho ảnh rõ nét trên màn thì tiêu cự thấu kính tính theo công thức: $\text{f =}\frac{{{\text{L}}^{2}}-{{\ell }^{2}}}{4.\text{L}}$
CÁC DẠNG BÀI TẬP
DẠNG 1: BÀI TOÁN LIÊN QUAN ĐẾN TIÊU CỰ, ĐỘ TỤ.
|
Bài tập 1: Thủy tinh làm thấu kính có chiết suất n = 1,5. a) Tìm tiêu cự của các thấu kính khi đặt trong không khí. Nếu: +) Hai mặt lồi có bán kính 10 cm, 30 cm +) Mặt lồi có bán kính 10 cm, mặt lõm có bán kính 30 cm. b) Tính lại tiêu cự của thấu kính trên khi chúng được dìm vào trong nước có chiết suất n1 = 4/3. |
Lời giải chi tiết:
a) Ta có: $\text{D =}\frac{1}{\text{f}}=\left( \frac{\text{n}}{\text{n }\!\!’\!\!\text{ }}-1 \right)\left( \frac{1}{{{\text{R}}_{1}}}+\frac{1}{{{\text{R}}_{2}}} \right)$
Khi thấu kính đặt trong không khí thì: $\text{n }\!\!’\!\!\text{ }$= 1
Khi hai mặt lồi có bán kính 10 cm, 30 cm thì: R1 = 10cm; R2 = 30cm
$\Rightarrow \frac{1}{\text{f}}=\left( \frac{1,5}{1}-1 \right)\left( \frac{1}{10}+\frac{1}{30} \right)\Rightarrow \text{f = 15 (cm)}$
Khi mặt lồi có bán kính 10 cm, mặt lõm có bán kính 30 cm thì: R1 = 10cm; R2 = –30cm
$\Rightarrow \frac{1}{\text{f}}=\left( \frac{1,5}{1}-1 \right)\left( \frac{1}{10}+\frac{1}{-30} \right)\Rightarrow \text{f = 30 (cm)}$
b) Khi dìm trong nước thì n’ = 4/3
Hai mặt lồi có bán kính 10 cm, 30 cm: $\frac{1}{\text{f}}=\left( \frac{1,5}{4/3}-1 \right)\left( \frac{1}{10}+\frac{1}{30} \right)\Rightarrow \text{f = 60 (cm)}$
Mặt lồi R = 10 cm, mặt lõm có R2 = – 30cm: $\frac{1}{\text{f}}=\left( \frac{1,5}{4/3}-1 \right)\left( \frac{1}{10}+\frac{1}{-30} \right)\Rightarrow \text{f = 120 (cm)}$
|
Bài tập 2: Một thấu kính hai mặt lồi Khi đặt trong không khí, thấu kính có độ tụ D1; khi đặt trong chất lỏng có chiết suất n’ = 1,68 thấu kính lại có độ tụ ${{\text{D}}_{2}}=-\frac{{{\text{D}}_{1}}}{5}$. a) Tính chiết suất n của thấu kính. b) Cho D1 = 2,5dp và biết rằng một mặt có bán kính cong gấp 4 lần bán kính cong của mặt kia. Hãy tính các bán kính cong của hai mặt thấu kính. |
Lời giải chi tiết:
Khi thấu kính đặt trong không khí thì: ${{\text{D}}_{1}}=\left( \text{n – 1} \right)\left( \frac{1}{{{\text{R}}_{1}}}+\frac{1}{{{\text{R}}_{2}}} \right)$ $\left( 1 \right)$
Khi thấu kính đặt trong chất lỏng có chiết suất n’ thì: ${{\text{D}}_{2}}=\left( \frac{\text{n}}{\text{n }\!\!’\!\!\text{ }}\text{ – 1} \right)\left( \frac{1}{{{\text{R}}_{1}}}+\frac{1}{{{\text{R}}_{2}}} \right)$ $\left( 2 \right)$
a) Từ $\left( 1 \right)$và $\left( 2 \right)$ta có: $\frac{{{\text{D}}_{2}}}{{{\text{D}}_{1}}}=\frac{\frac{\text{n}}{\text{n }\!\!’\!\!\text{ }}\text{ – 1}}{\text{n – 1}}\Leftrightarrow \frac{-1}{5}=\frac{\frac{\text{n}}{1,68}-1}{\text{n}-1}$
$\Leftrightarrow 5.\left( \frac{\text{n}}{1,68}-1 \right)=\left( 1-\text{n} \right)\Leftrightarrow \frac{167}{42}\t
ext{n}=6\Rightarrow \text{n}=1,5.$
b) Từ: ${{\text{D}}_{1}}=\left( \text{n}-1 \right)\left( \frac{1}{{{\text{R}}_{1}}}+\frac{1}{{{\text{R}}_{2}}} \right)\Leftrightarrow 2,5=\left( 1,5-1 \right)\left( \frac{1}{{{\text{R}}_{1}}}+\frac{1}{4{{\text{R}}_{1}}} \right).$
$\Rightarrow $R1 = 0,25m = 25cm và R2 = 4R1 = 4.25 = 100cm.
|
Bài tập 3: Một thấu kính bằng thuỷ tinh (chiết suất n = 1,5) đặt trong không khí có độ tụ 8 điôp. Khi nhúng thấu kính vào một chất lỏng nó trở thành một thấu kính phân kì có tiêu cự 1m. Tính chiết suất của chất lỏng. |
Lời giải chi tiết:
Khi đặt thấu kính trong không khí thì: $\text{D =}\left( 1,5-1 \right)\left( \frac{1}{{{\text{R}}_{1}}}+\frac{1}{{{\text{R}}_{2}}} \right)=8\text{dp}$ (1)
Khi đặt thấu kính trong chất lỏng có chiết suất n’ thì: ${{\text{D}}_{1}}=\left( \frac{1,5}{\text{n }\!\!’\!\!\text{ }}-1 \right)\left( \frac{1}{{{\text{R}}_{1}}}+\frac{1}{{{\text{R}}_{2}}} \right)=-1\text{dp}$ (2)
Từ (1) và (2) ta có: $-8=\frac{\left( 1,5-1 \right)}{\left( \frac{1,5}{\text{n }\!\!’\!\!\text{ }}-1 \right)}\Rightarrow \left( \frac{1,5}{\text{n }\!\!’\!\!\text{ }}-1 \right)=\frac{-1}{16}\Rightarrow \text{n }\!\!’\!\!\text{ }=1,6.$
DẠNG 2. XÁC ĐỊNH VỊ TRÍ VẬT, ẢNH, KÍCH THƯỚC ẢNH.
|
Bài tập 4: Vật sáng AB đặt vuông góc với trục chính của một thấu kính hội tụ có tiêu cự f = 20 cm. Xác định tính chất, chiều, độ lớn của ảnh qua thấu kính và vẽ hình trong những trường hợp sau: a) Vật cách thấu kính 30 cm. b) Vật cách thấu kính 20 cm. c) Vật cách thấu kính 10 cm. |
Lời giải chi tiết:
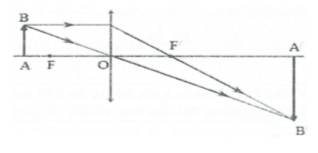a) Ta có: $\frac{1}{\text{f}}=\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}$
$\Rightarrow \text{d }\!\!’\!\!\text{ }=\frac{\text{df}}{\text{d}-\text{f}}=\frac{30.20}{30-20}=60\left( \text{cm} \right)>0$
Ảnh là ảnh thật và cách thấu kính đoạn 60 cm
Số phóng đại của ảnh: $\text{k}=-\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}}=-\frac{60}{30}=-2<0$
$\Rightarrow $ảnh ngược chiều với vật và lớn gấp 2 lần vật.
b) Ta có: $\frac{1}{\text{f}}=\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}$ $\Rightarrow \text{d }\!\!’\!\!\text{ }=\frac{\text{df}}{\text{d}-\text{f}}=\frac{20.20}{20-20}=+\infty $
$\Rightarrow $ảnh ở vô cùng.
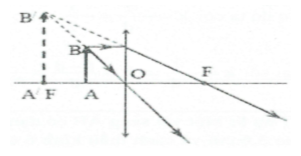
c) Ta có: $\frac{1}{\text{f}}=\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}$
$\Rightarrow \text{d }\!\!’\!\!\text{ }=\frac{\text{df}}{\text{d}-\text{f}}=\frac{10.20}{10-20}=-20\text{ (cm) 0}$: ảnh ảo và cách thấu
kính đoạn 20 cm.
Số phóng đại của ảnh: $\text{k}=-\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}}=-\frac{-20}{10}=2>0$
$\Rightarrow $ảnh cùng chiều với vật và lớn gấp 2 lần vật.
|
Bài tập 5: Một thấu kính hội tụ có tiêu cự 20 cm. Vật sáng AB là một đoạn thẳng đặt vuông góc trục chính của thấu kính cho ảnh cao gấp 2 lần vật. Xác định vị trí vật và ảnh. |
Lời giải chi tiết:
Ta có: $\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}=\frac{1}{\text{f}}$ $\Rightarrow \text{d }\!\!’\!\!\text{ = }\frac{\text{d}\text{.f}}{\text{d – f}}$
Theo bài ra, ảnh cao gấp 2 lần vật nên chưa thể xác định là ảnh thật hay ảnh ảo vì thế:
$\text{k}=\pm 2\Leftrightarrow -\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}}=\pm 2\Leftrightarrow \frac{\frac{\text{d}\text{.f}}{\text{f}-\text{d}}}{\text{d}}=\pm 2\Leftrightarrow \frac{\text{f}}{\text{f}-\text{d}}=\pm 2$
$\Leftrightarrow \frac{20}{(20-\text{d)}}=\pm 2\Rightarrow \left\{ \begin{array}{} 10=(20-\text{d)} \\ {} \text{10}=-(20-\text{d)} \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{} \text{d}=10\text{ (cm)}>0 \\{} \text{d}=30\text{ (cm) 0} \\ \end{array} \right.$(cả 2 vị trí đều thỏa mãn)
Khi vật cách thấu kính $\text{d}=10\text{ cm}\Rightarrow \text{d }\!\!’\!\!\text{ }=\frac{\text{d}\text{.f}}{\text{d}-\text{f}}=\frac{10.20}{10-20}=-20\left( \text{cm} \right)<0$
Khi vật cách thấu kính $\text{d}=30\text{ cm}\Rightarrow \text{d }\!\!’\!\!\text{ }=\frac{\text{d}\text{.f}}{\text{d}-\text{f}}=\frac{30.20}{30-20}=60\left( \text{cm} \right)>0.$
|
Bài tập 6: Một thấu kính hội tụ có tiêu cự 20 cm. Vật sáng AB là một đoạn thẳng đặt vuông góc trục chính của thấu kính cho ảnh cao bằng vật. Xác định vị trí vật và ảnh. |
Lời giải chi tiết:
Vật thật qua thấu kính hội tụ cho ảnh bằng vật $\Rightarrow $ảnh thật $\Rightarrow $ $\left\{ \begin{array}{} \text{d }\!\!’\!\!\text{ }>0 \\ {} \text{k}<0 \\ \end{array} \right.$
Ta có: $\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}=\frac{1}{\text{f}}\Rightarrow \text{d }\!\!’\!\!\text{ }=\frac{\text{d}\text{.f}}{\text{d}-\text{f}}$
Theo bài ra ta có: $\text{k}=-1\Leftrightarrow -\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}}=-1\Leftrightarrow \frac{\frac{\text{d}\text{.f}}{\text{d}-\text{f}}}{\text{d}}=1\Leftrightarrow \frac{\text{f}}{\text{d}-\text{f}}=1\Rightarrow \text{d}=2\text{f}=40\left( \text{cm} \right)$
$\Rightarrow \text{d }\!\!’\!\!\text{ }=\frac{\text{d}\text{.f}}{\text{d}-\text{f}}=\frac{40.20}{40-20}=40\left( \text{cm} \right)>0.$
|
Bài tập 7: Một thấu kính hội tụ có tiêu cự f = 20 cm. Vật sáng AB cao 2 cm cho ảnh A’B’ cao l cm. Tính độ phóng đại của ảnh và xác định vị trí vật? |
Lời giải chi tiết:
Vật thật qua thấu kính hội tụ cho ảnh nhỏ hơn vật nên ảnh đó chỉ có thể là ảnh thật (vì ảnh ảo qua thấu kính hội tụ luôn lớn hơn vật).
Do đó ta có: $\text{k}=-\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}}=-\frac{1}{2}.$Mà: $\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}=\frac{1}{\text{f}}\Rightarrow \text{d }\!\!’\!\!\text{ }=\frac{\text{d}\text{.f}}{\text{d}-\text{f}}$
Lại có: $\text{k}=-\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}}\Rightarrow \text{k}=\frac{\frac{\text{d}\text{.f}}{\text{f}-\text{d}}}{\text{d}}=\frac{\text{f}}{\text{f}-\text{d}}\Leftrightarrow -\frac{1}{2}=\frac{\text{f}}{\text{f}-\text{d}}\Leftrightarrow -\frac{1}{2}=\frac{20}{20-\text{d}}\Rightarrow \text{d}=60\left( \text{cm} \right).$
|
Bài tập 8: Một vật sáng AB có dạng mũi tên đặt vuông góc trục chính của thấu kính phân kỳ, cho ảnh cao 3,6 cm và cách thấu kính 6 cm. Thấu kính có tiêu cự 15 cm. Xác định vị trí và kích thước của vật. Vẽ hình. |
Lời giải chi tiết:
Áp dụng công thức thấu kính ta có: $\frac{1}{\text{f}}=\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}\Rightarrow \text{d}=\frac{\text{d }\!\!’\!\!\text{ }\text{.f}}{\text{d }\!\!’\!\!\text{ }-\text{f}}$
Vì thấu kính phân kì nên f = -15 (cm) và vật thật cho ảnh ảo nên d’ = -6 (cm)
Vị trí của vật AB: $\text{d}=\frac{\text{d }\!\!’\!\!\text{ }\text{.f}}{\text{d }\!\!’\!\!\text{ }-\text{f}}=\frac{\left( -6 \right)\left( -15 \right)}{\left( -6 \right)-\left( -15 \right)}=10\left( \text{cm} \right)$
Kích thước (chiều cao) của vật: $\text{AB}=\frac{\text{A }\!\!’\!\!\text{ B }\!\!’\!\!\text{ }}{\left| \text{k} \right|}=\frac{\text{A }\!\!’\!\!\text{ B }\!\!’\!\!\text{ }}{\left| -\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}} \right|}=\frac{3,6}{\frac{6}{10}}=6\left( \text{cm} \right).$
|
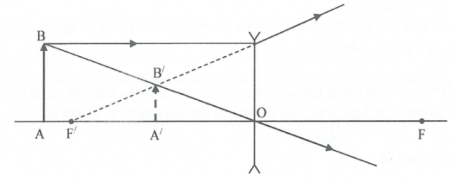
Bài tập 9: Chứng tỏ rằng thấu kính hội tụ luôn luôn tạo được: a) ảnh ảo lớn hơn vật thật. b) ảnh thật nhỏ hơn vật ảo. |
Lời giải chi tiết
a) Ta có: Vật thật: d > 0; thấu kính hội tụ: f > 0; ảnh ảo: d’ < 0.
Mà: $\text{d }\!\!’\!\!\text{ =}\frac{\text{df}}{\text{d}-\text{f}}\Leftrightarrow \frac{\text{df}}{\text{d}-\text{f}}<0\Rightarrow 0<\text{d f; }$Số phóng đại: $\left| \text{k} \right|=\left| -\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}} \right|=\left| \frac{\text{f}}{\text{f}-\text{d}} \right|>1.$
b) Ta có: Vật ảo: d 0; ảnh thật: d’ > 0.
Mà: $\text{d }\!\!’\!\!\text{ =}\frac{\text{df}}{\text{d}-\text{f}}\Leftrightarrow \frac{\text{df}}{\text{d}-\text{f}}>0\Rightarrow \text{d }\!\!’\!\!\text{ 0}$ (với mọi d < 0);
Số phóng đại: $\left| \text{k} \right|=\left| -\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}} \right|=\left| \frac{\text{f}}{\text{f}-\text{d}} \right|<1.$
DẠNG 3. LIÊN QUAN ĐẾN KHOẢNG CÁCH VẬT ẢNH.
Áp dụng các công thức về ảnh tạo bởi thấu kính: $\left\{ \begin{array}{} \text{d }\!\!’\!\!\text{ }=\frac{\text{df}}{\text{d}-\text{f}} \\ {} \text{k =}-\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}}=\frac{\text{f}}{\text{f}-\text{d}} \\ \end{array} \right.$
Vật và ảnh cùng tính chất thì trái chiều và ngược lại
Trong mọi trường hợp khoảng cách giữa vật và ảnh là: $\text{L}=\left| \text{d}+\text{d }\!\!’\!\!\text{ } \right|.$
|
Bài tập 10: Một màn ảnh đặt song song với vật sáng AB và cách AB một đoạn L. Một thấu kính hội tụ có tiêu cự f đặt trong khoảng giữa vật và màn sao cho AB vuông góc với trục chính của thấu kính. Tìm mối liên hệ giữa L và f để a) có 2 vị trí của thấu kính cho ảnh rõ nét trên màn. b) có 1 vị trí của thấu kính cho ảnh rõ nét trên màn. c) không có vị trí của thấu kính cho ảnh rõ nét trên màn. |
Lời giải chi tiết:
Vì ảnh hứng trên màn là ảnh thật nên d’ > 0 $\Rightarrow \text{L}=\text{d}+\text{d }\!\!’\!\!\text{ }$
Ta có: $\text{d}=\frac{\text{d }\!\!’\!\!\text{ }\text{.f}}{\text{d }\!\!’\!\!\text{ }-\text{f}}\Rightarrow \text{L}=\frac{\text{d }\!\!’\!\!\text{ }\text{.f}}{\text{d }\!\!’\!\!\text{ }-\text{f}}+\text{d }\!\!’\!\!\text{ }\Leftrightarrow \text{L}\left( \text{d }\!\!’\!\!\text{ }-\text{f} \right)={{\left( \text{d }\!\!’\!\!\text{ } \right)}^{2}}\Rightarrow {{\left( \text{d }\!\!’\!\!\text{ } \right)}^{2}}-\text{L}\text{.d }\!\!’\!\!\text{ }+\text{f}\text{.L}=0$ (*)
Ta có: $\Delta ={{\text{b}}^{2}}-4\text{ac}={{\text{L}}^{2}}-4\text{fL}$
a) Để có hai ảnh rõ nét trên màn thì phương trình (*) phải có hai nghiệm phân biệt hay $\Delta >0\Leftrightarrow {{\text{L}}^{2}}-4\text{fL}>0\Rightarrow \text{L}-\text{4f}>0\Rightarrow \text{L}>\text{4f}$
b) Để có 1 vị trí của thấu kính cho ảnh rõ nét trên màn thì phương trình (*) phải có nghiệm kép hay
$\Delta =0\Leftrightarrow {{\text{L}}^{2}}-4\text{fL = }0\Rightarrow \text{L}-\text{4f = }0\Rightarrow \text{L = 4f}$
c) Để không có vị trí của thấu kính cho ảnh rõ nét trên màn thì phương trình (*) phải vô nghiệm hay
$\Delta <0\Leftrightarrow {{\text{L}}^{2}}-4\text{fL }0\Rightarrow \text{L}-\text{4f }0\Rightarrow \text{L 4f}$.
|
Bài tập 11: Một vật sáng AB = 4mm đặt thẳng góc với trục chính của một thấu kính hội tụ có tiêu cự 40 cm, cho ảnh cách vật 36 cm. Xác định vị trí, tính chất và độ lớn của ảnh và vị trí của vật. |
Lời giải chi tiết:
Ta có: $\text{L}=\left| \text{d}+\text{d }\!\!’\!\!\text{ } \right|=36\Leftrightarrow \text{d}+\text{d }\!\!’\!\!\text{ }=\pm 36$
Ta có: $\text{d }\!\!’\!\!\text{ }=\frac{\text{df}}{\text{d}-\text{f}}\Rightarrow \text{L}=\text{d}+\frac{\text{df}}{\text{d}-\text{f}}=\pm 36\Leftrightarrow {{\text{d}}^{2}}=\pm 36\left( \text{d}-\text{f} \right)\Leftrightarrow {{\text{d}}^{2}}=\pm 36\left( \text{d}-40 \right)$
$\Leftrightarrow {{\text{d}}^{2}}=\pm 36\left( \text{d}-40 \right)\Rightarrow \left\{ \begin{array}{} {{\text{d}}^{2}}-36\text{d}+36.40=0\text{ }\left( 1 \right) \\ {} {{\text{d}}^{2}}+36\text{d}-36.40=0\text{ }\left( 2 \right) \\ \end{array} \right.$
Giải (1): ${{\text{d}}^{2}}-36\text{d}+36.40=0\Rightarrow $vô nghiệm
Giải (2): d2 + 36d – 36.40 = 0 $\Rightarrow $ 
Vị trí ảnh: $\text{d }\!\!’\!\!\text{ }=\frac{\text{df}}{\text{d}-\text{f}}=\frac{24.40}{24-40}=-60\left( \text{cm} \right)<0\Rightarrow $ảnh ảo
Số phóng đại của ảnh: $\text{k}=-\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}}\Rightarrow \text{k}=-\frac{-60}{24}=2,5>0\Rightarrow $ảnh cùng chiều với vật.
Độ lớn của ảnh: $\text{A }\!\!’\!\!\text{ B }\!\!’\!\!\text{ }=\left| \text{k} \right|\text{AB}=2,5.4=10\left( \text{mm} \right).$
|
Bài tập 12: Đặt 1 vật sáng AB có chiều cao 2 cm trước 1 thấu kính hội tụ có tiêu cự f = 20 cm. Cách vật AB đoạn 90 cm người ta đặt 1 màn hứng. a) Hãy tìm vị trí đặt thấu kính để có thể hứng ảnh rõ nét trên màn? b) Tìm độ cao của ảnh trong câu a? |
Lời giải chi tiết:
a) Vì ảnh hứng trên màn nên $\text{L}=\text{d}+\text{d }\!\!’\!\!\text{ }=90$
Ta có: $\text{d }\!\!’\!\!\text{ }=\frac{\text{df}}{\text{d}-\text{f}}\Leftrightarrow \text{d}+\text{d }\!\!’\!\!\text{ }=90\Leftrightarrow \text{d}+\frac{\text{df}}{\text{d}-\text{f}}=90$
$\Leftrightarrow {{\text{d}}^{2}}=90\left( \text{d}-\text{f} \right)\Rightarrow {{\text{d}}^{2}}-90\text{d}+90\text{f}=0\Leftrightarrow {{\text{d}}^{2}}-90\text{d}+1800=0\Rightarrow \left[ \begin{array}{} {{\text{d}}_{1}}=30\left( \text{cm} \right) \\ {} {{\text{d}}_{2}}=6
