LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
Phương pháp chung:
Con lắc bị ảnh hưởng bởi lực quán tính
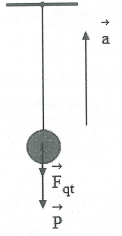
a) Khi điểm treo con lắc có gia tốc $\overrightarrow{\text{a}}$hướng thẳng đứng lên trên.
|
(Điểm treo chuyển động thẳng đứng lên trên nhanh dần đều hoặc chuyển động thẳng đứng xuống dưới chấm dần đều). Ta có: $\overrightarrow{{\text{{P}’}}}\text{=}\overrightarrow{\text{P}}\text{+}\overrightarrow{{{\text{F}}_{\text{qt}}}}\left( \text{1} \right)$ Chọn chiều dương Ox hướng xuống. Chiếu $\left( 1 \right)$lên trục Ox ta có: $\mathrm{{P}’=P+}{{\mathrm{F}}_{\mathrm{qt}}}\mathrm{=mg+ma}\Rightarrow \mathrm{{g}’=g+a}\Rightarrow \mathrm{{T}’=2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{\mathrm{g+a}}}\mathrm{.}$ Khi đó: $\frac{{\text{{T}’}}}{\text{T}}\text{=}\sqrt{\frac{\text{g}}{\text{g+a}}}$ (với T là chu kì của con lắc khi thang máy đứng yên hay chuyển động thằng đều). |
|
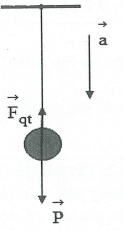
b) Khi điểm treo con lắc có gia tốc $\overrightarrow{\text{a}}$ hướng thẳng đứng xuống dưới.
|
(Điểm treo con lắc chuyển động thẳng đứng đi xuống nhanh dần đều hoặc chuyển động thẳng đứng lên trên chậm dần đều) Chiếu $\left( 1 \right)$lên trục Ox ta có: $\text{{P}’}=\text{P}-{{\text{F}}_{\text{qt}}}=\text{mg}-\text{ma}\Rightarrow \text{{g}’}=\text{g}-\text{a}\Rightarrow \text{{T}’}=2\pi \sqrt{\frac{\ell }{\text{g}-a}}.$ (Chú ý: $\text{g a}$) Khi đó: $\frac{{\mathrm{{T}’}}}{\mathrm{T}}\mathrm{=}\sqrt{\frac{\mathrm{g}}{\mathrm{g}-\mathrm{a}}}$(với T là chu kì của con lắc khi thang máy đứng yên hay chuyển động thẳng đều). |
|
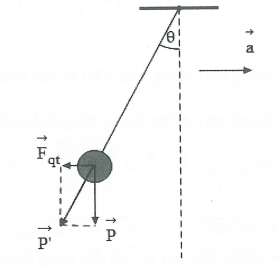
c) Khi điểm treo con lắc có gia tốc $\overrightarrow{\text{a}}$ hướng sang ngang.
|
Ta có: $\overrightarrow{{{\text{F}}_{\text{qt}}}}$có phương ngang và ngược hướng với gia tốc $\overrightarrow{\text{a}}$. Vị trí cân bằng được xác định bởi góc $\text{ }\!\!\theta\!\!\text{ }$. Tại vị trí cân bằng dây treo hợp với phương thẳng đứng một góc $\text{ }\!\!\theta\!\!\text{ }$. Ta có: $\text{tan }\!\!\theta\!\!\text{ }=\frac{{{\text{F}}_{\text{qt}}}}{\text{P}}=\frac{\text{ma}}{\text{mg}}=\frac{\text{a}}{\text{g}}.$ Mặt khác ${{\text{{P}’}}^{\text{2}}}={{\text{P}}^{\text{2}}}+\text{F}_{\text{qt}}^{\text{2}}\Rightarrow \text{{g}’}=\sqrt{{{\text{g}}^{\text{2}}}+{{\text{a}}^{\text{2}}}}.$ Chu kì dao động của con lắc: $\text{{T}’}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{{\text{{g}’}}}}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{\sqrt{{{\text{g}}^{\text{2}}}+{{\text{a}}^{\text{2}}}}}}$ |
|
Hoặc: Ta có: $\text{{P}’}=\frac{\text{P}}{\text{cos }\!\!\theta\!\!\text{ }}\Rightarrow \text{{g}’}=\frac{\text{g}}{\text{cos }\!\!\theta\!\!\text{ }}\Rightarrow \text{{T}’}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{{\text{{g}’}}}}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell \cos \alpha }{\text{g}}}.$
Con lắc đơn dưới tác dụng của lực đẩy Asimet
Trong chân không ta có: $\text{T}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{\text{g}}}.$
Trong không khí hoặc chất lỏng: $\overrightarrow{{\text{{P}’}}}=\overrightarrow{\text{P}}+\overrightarrow{{{\text{F}}_{\text{ }\!\!\Alpha\!\!\text{ }}}}.$
Ta có: $\overrightarrow{{{\text{F}}_{\text{ }\!\!\Alpha\!\!\text{ }}}}=-\text{DV}\overrightarrow{\text{g}}$ luôn hướng lên và ngược chiều với $\overrightarrow{\text{P}}$.
Do đó $\text{{P}’}=\text{P}-{{\text{F}}_{\text{ }\!\!\Alpha\!\!\text{ }}}\Rightarrow \text{{g}’}=\text{g}-\frac{\text{DVg}}{\text{ }\!\!\rho\!\!\text{ V}}=\left( 1-\frac{\text{D}}{\text{ }\!\!\rho\!\!\text{ }} \right)\text{g}\Rightarrow \frac{{\text{{T}’}}}{\text{T}}=\sqrt{\frac{1}{1-\frac{\text{D}}{\text{ }\!\!\rho\!\!\text{ }}}}\Rightarrow \text{{T}’}=\text{T}\sqrt{\frac{1}{1-\frac{\text{D}}{\text{ }\!\!\rho\!\!\text{ }}}}.$
Trong đó: D là khối lượng chất lỏng (hay chất khí) bị chiếm chỗ.
$\text{ }\!\!\rho\!\!\text{ }$là khối lượng riêng của quả cầu.
V là thể tích vật chiếm chỗ.
g là gia tốc trọng trường.