BÀI TẬP TỔNG HỢP DAO ĐỘNG ĐIỀU HÒA CÓ ĐÁP ÁN CHI TIẾT
Dạng 1. Tổng hợp 2 hay nhiều dao động.
| Bài tập 1: [Trích đề thi đại học năm 2013]. Hai dao động điều hòa cùng phương, cùng tần số có biên độ lần lượt là ${{A}_{1}}=8$cm, ${{A}_{2}}=15$cm và lệch pha nhau $\frac{\pi }{2}$ . Dao động tổng hợp của hai dao động này có biên độ bằng
A. 7 cm. B. 11 cm. C. 17 cm. D. 23 cm. |
Lời giải chi tiết:
Hai dao động vuông pha ${{\varphi }_{1}}-{{\varphi }_{2}}=\frac{\pi }{2}\Rightarrow A=\sqrt{A_{1}^{2}+A_{2}^{2}}=17$cm. Chọn C.
| Bài tập 2: Hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ có pha ban đầu lần lượt là $\frac{\pi }{6}$ và $\frac{2\pi }{3}$ . Pha ban đầu của dao động tổng hợp của hai dao động trên là
A. $\frac{-\pi }{2}$ . B. $\frac{5\pi }{12}$ . C. $\frac{-5\pi }{12}$ . D. $\frac{\pi }{2}$ . |
Lời giải chi tiết:
Cách 1: Ta có: $\tan \varphi =\frac{{{A}_{1}}\sin {{\varphi }_{1}}+{{A}_{2}}\sin {{\varphi }_{2}}}{{{A}_{1}}\cos {{\varphi }_{1}}+{{A}_{2}}\cos {{\varphi }_{2}}}=\frac{\sin \frac{\pi }{6}+\sin \frac{2\pi }{3}}{\cos \frac{\pi }{6}+\cos \frac{2\pi }{3}}=2+\sqrt{3}\Rightarrow \varphi =\frac{5\pi }{12}$ .
Cách 2: CASIO: Chọn ${{A}_{1}}={{A}_{2}}=1$ .
Ta có: $x=1\angle \frac{\pi }{6}+1\angle \frac{2\pi }{3}=\sqrt{2}\angle \frac{5\pi }{12}$ . Chọn B.
| Bài tập 3: Một vật thực hiện đồng thời 2 dao động điều hòa với biên độ lần lượt là 3 cm và 5 cm. Trong các giá trị sau giá trị nào không thể là biên bộ của dao động tổng hợp.
A. 4 cm. B. 5 cm. C. 3 cm. D. 10 cm. |
Lời giải chi tiết:
Ta có: $\left| {{A}_{1}}-{{A}_{2}} \right|\le A\le {{A}_{1}}+{{A}_{2}}\Rightarrow 2cm\le A\le 8cm$ . Chọn D.
| Bài tập 4: Chuyển động của một vật là tổng hợp của hai dạo động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là ${{x}_{1}}=4\cos \left( 10t+\frac{\pi }{4} \right)cm$ và ${{x}_{2}}=3\cos \left( 10t-\frac{3\pi }{4} \right)cm$ . Độ lớn vận tốc của vật này ở vị trí cân bằng là
A. 80 $cm/s$ . B. 100 $cm/s$ . C. 10 $cm/s$ . D. 50 $cm/s$ . |
Lời giải chi tiết:
Cách 1: Ta có biên độ dao động tổng hợp: ${{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \left( {{\varphi }_{1}}-{{\varphi }_{2}} \right)$
Do hai dao động ngược pha nên $A=\left| {{A}_{1}}-{{A}_{2}} \right|$
Suy ra $A=1cm$ do đó ${{v}_{\max }}=\omega A=10cm/s$ .
Cách 2: $x={{x}_{1}}+{{x}_{2}}=4\angle \frac{\pi }{4}+3\angle \frac{-3\pi }{4}=1\angle \frac{\pi }{4}$
Suy ra $x=\cos \left( 10t+\frac{\pi }{4} \right)cm\Rightarrow {{v}_{\max }}=10cm/s$ . Chọn C.
| Bài tập 5: [Đề thi thử chuyên ĐH Vinh 2017]. Một chất điểm tham gia đồng thời hai dao động điều hòa cùng phương cùng tần số. Biết dao động thành phần thứ nhất có biên độ dao động ${{A}_{1}}=4\sqrt{3}$cm, dao động tổng hợp có biên độ $A=4$ cm. Dao động thành phần thứ hai sớm pha hơn dao động tổng hợp là $\frac{\pi }{3}$ . Dao động thành phần thứ hai có biên độ ${{A}_{2}}$ là
A. $4\sqrt{3}$ cm. B. $6\sqrt{3}$ cm. C. 4 cm. D. 8 cm. |
Lời giải chi tiết:
Ta có: ${{x}_{1}}=x-{{x}_{2}}\Rightarrow A_{1}^{2}={{A}^{2}}+A_{2}^{2}-2A{{A}_{2}}\cos \frac{\pi }{3}\Leftrightarrow 48=16+A_{2}^{2}-4{{A}_{2}}\Rightarrow {{A}_{2}}=8$ cm. Chọn D.
| Bài tập 6: [Trích đề thi đại học năm 2010]. Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số có phương trình li độ $x=3\cos \left( \pi t=\frac{5\pi }{6} \right)$ cm. Biết dao động thư nhất có phương trình li độ ${{x}_{1}}=5\cos \left( \pi t+\frac{\pi }{6} \right)$ cm. Dao động thứ hai có phương trình li độ là
A. ${{x}_{2}}=8\cos \left( \pi t+\frac{\pi }{6} \right)$ cm. B. ${{x}_{2}}=2\cos \left( \pi t+\frac{\pi }{6} \right)$ cm. C. ${{x}_{2}}=2\cos \left( \pi t-\frac{5\pi }{6} \right)$ cm. D. ${{x}_{2}}=8\cos \left( \pi t-\frac{5\pi }{6} \right)$ cm. |
Lời giải chi tiết:
Cách 1: Ta có: ${{x}_{2}}=x-{{x}_{1}}=3\cos \left( \pi t-\frac{5\pi }{6} \right)-5\cos \left( \pi t+\frac{\pi }{6} \right)$
$=3\cos \left( \pi t-\frac{5\pi }{6} \right)+5\cos \left( \pi t-\frac{5\pi }{6} \right)=8\cos \left( \pi t-\frac{5\pi }{6} \right)$ .
Cách 2: CASIO: ${{x}_{2}}=x-{{x}_{1}}=3\angle -\frac{5\pi }{6}-5\angle \frac{\pi }{6}=8\angle \frac{-5\pi }{6}$ . Chọn C.
| Bài tập 7: Một chất điểm tham gia đồng thời hai dao động có các phương trình ${{x}_{1}}={{A}_{1}}\cos \left( \omega t+\frac{\pi }{6} \right)$ cm; ${{x}_{2}}=\sqrt{3}\cos \left( \omega t+\varphi \right)$ . Phương trình dao động tổng hợp là $x=\frac{3}{2}\cos \left( \omega t+\frac{2\pi }{3} \right)$ cm. Giá trị của ${{A}_{1}}$ và $\varphi $ là
A. ${{A}_{1}}=\frac{\sqrt{3}}{2};\varphi =\frac{\pi }{6}$ . B. ${{A}_{1}}=\frac{\sqrt{3}}{2};\varphi =\frac{5\pi }{6}$ . C. ${{A}_{1}}=\sqrt{3};\varphi =\frac{\pi }{6}$ . D. ${{A}_{1}}=\sqrt{3};\varphi =\frac{5\pi }{6}$ . |
Lời giải chi tiết:
Ta có: ${{x}_{2}}=x-{{x}_{1}}\Rightarrow A_{2}^{2}={{A}^{2}}+A_{1}^{2}-2A{{A}_{1}}\cos \frac{\pi }{2}$
![]() suy ra
suy ra ![]() . Chọn B.
. Chọn B.
| Bài tập 8: Một vật thực hiện đồng thời hai dao động điều hòa ${{x}_{1}}=A\cos \left( 10\pi t+\frac{\pi }{3} \right)$; ${{x}_{2}}=B\cos \left( 10\pi t-\frac{\pi }{2} \right)$ . Khi ${{x}_{2}}=0,5B\sqrt{3}$ và đang tăng thì vận tốc của vật bằng $-80\pi $ cm/s độ lớn thì bằng một nửa giá trị cực đại. Giá trị của A là
A. $8\sqrt{3}$ cm. B. 16 cm. C. $16\sqrt{3}$ cm. D. 32 cm. |
Lời giải chi tiết:
| Biên độ tổng hợp: $80\pi =\frac{{{A}_{th}}.10\pi }{2}\Rightarrow {{A}_{th}}=16$cm
Khi v âm và $\left| v \right|=\frac{{{v}_{\max }}}{2}\Rightarrow x=\frac{{{A}_{th}}\sqrt{3}}{2}$ (theo chiều âm) Tại thời điểm ${{x}_{2}}=0,5B\sqrt{3}$ kết hợp ${{x}_{1}}$ pha nhanh $120{}^\circ $ so với ${{x}_{2}}$ , ta có giản đồ vecto: $\Rightarrow \overrightarrow{A}\bot \overrightarrow{{{A}_{th}}}\Rightarrow A={{A}_{th}}.\tan 60{}^\circ =16.tan60{}^\circ =16\sqrt{3}$ cm. Chọn C. |
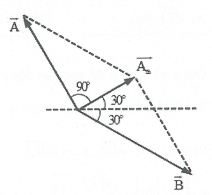 |
| Bài tập 9: [Đề thi thử chuyên Quốc Học Huế 2017]. Một vật thực hiện đồng thời ba dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là ${{x}_{1}}={{A}_{1}}\cos \left( 2\pi t+\frac{2\pi }{3} \right)$ cm, ${{x}_{2}}={{A}_{2}}\cos \left( 2\pi t \right)$ , ${{x}_{3}}={{A}_{3}}\cos \left( 2\pi t-\frac{2\pi }{3} \right)$ cm. Tại thời điểm ${{t}_{1}}$ các giá trị có li độ là ${{x}_{1}}=-20$ cm, ${{x}_{2}}=80$ cm, ${{x}_{3}}=40$ cm. Tại thời điểm ${{t}_{2}}={{t}_{1}}+\frac{T}{4}$ các giá trị li độ ${{x}_{1}}=-20\sqrt{3}$ cm, ${{x}_{2}}=0$ cm, ${{x}_{3}}=40\sqrt{3}$ cm. Phương trình của dao động tổng hợp là
A. $x=50\cos \left( 2\pi t+\frac{\pi }{3} \right)$ cm. B. $x=40\cos \left( 2\pi t+\frac{\pi }{3} \right)$ cm. C. $x=40\cos \left( 2\pi t-\frac{\pi }{3} \right)$ cm. D. $x=20\cos \left( 2\pi t-\frac{\pi }{3} \right)$ cm. |
Lời giải chi tiết:
Li độ tại thời điểm ${{t}_{1}}$ và ${{t}_{2}}$ vuông pha nhau nên ta có
$\left\{ \begin{array}{} {{A}_{1}}=\sqrt{{{\left( -20 \right)}^{2}}+{{\left( -20\sqrt{3} \right)}^{2}}}=40cm \\ {} {{A}_{2}}=\sqrt{{{80}^{2}}+{{0}^{2}}}=80cm \\ {} {{A}_{3}}=\sqrt{{{40}^{2}}+{{\left( 40\sqrt{3} \right)}^{2}}}=80cm \\ \end{array} \right.$ .
Khi đó: $x={{x}_{1}}+{{x}_{2}}+{{x}_{3}}=40\angle \frac{2\pi }{3}+80\angle 0+80\angle -\frac{2\pi }{3}=40\angle -\frac{\pi }{3}$ . Chọn B.
| Bài tập 10: [Đề thi thử sở GD{}ĐT Vĩnh Phúc 2017]. Dao động của một chất điểm là sự tổng hợp của hai dao động điều hòa với phương trình lần lượt là ${{x}_{1}}=2A\cos \left( \omega t+{{\varphi }_{1}} \right)$ và ${{x}_{2}}=3A\cos \left( \omega t+{{\varphi }_{2}} \right)$ . Tại thời điểm mà tỉ số vận tốc và tỉ số li độ của dao động thứ hai so với dao động thứ nhất lần lượt là 1 và $-2$ thì li độ dao động tổng hợp bằng $\sqrt{15}$ cm. Tại thời điểm mà tỉ số vận tốc và tỉ số li độ của dao động thứ hai so với dao động thứ nhất lần lượt là $-2$ và 1 thì li độ dao động tổng hợp của chất điểm có thể bằng
A. $\sqrt{15}$ cm. B. $2\sqrt{15}$ cm. C. $\sqrt{15}$ cm. D. $2\sqrt{21}$ cm. |
Lời giải chi tiết:
Gọi $x$ và ${x}’$ là li độ của dao động tổng hợp tại 2 thời điểm $t$ và ${t}’$
Tại thời điểm $t$: ta có $\text{x}={{x}_{1}}+{{x}_{2}}=\sqrt{15}$ và $\frac{{{x}_{2}}}{{{x}_{1}}}=-2$ .
Suy ra ${{\text{x}}_{1}}=-\sqrt{15}$, ${{\text{x}}_{2}}=2\sqrt{15}$ .
Lại có: $\left| \frac{{{v}_{2}}}{{{v}_{1}}} \right|=\frac{\sqrt{9{{A}^{2}}-x_{2}^{2}}}{\sqrt{4{{A}^{2}}-x_{1}^{2}}}=1\Rightarrow 9{{\text{A}}^{2}}-60=4{{\text{A}}^{2}}-15\Rightarrow A=3$ cm.
Tại thời điểm ${t}’$ ta có: $\left| \frac{{{v}_{2}}^{\prime }}{{{v}_{1}}^{\prime }} \right|=\sqrt{\frac{9{{\text{A}}^{2}}-{{\left( {{x}_{2}}^{\prime } \right)}^{2}}}{4{{A}^{2}}-{{\left( {{x}_{1}}^{\prime } \right)}^{2}}}}=2\Rightarrow 81-{{\left( {{x}_{1}}^{\prime } \right)}^{2}}=4\left[ 36-{{\left( {{x}_{1}}^{\prime } \right)}^{2}} \right]$
$\Rightarrow {{x}_{1}}^{\prime }={{x}_{2}}^{\prime }=\sqrt{21}\Rightarrow {x}’={{x}_{1}}^{\prime }+{{x}_{2}}^{\prime }=2\sqrt{21}$ . Chọn D.
| Bài tập 11: Một vật thực hiện đồng thời ba dao động điều hòa cùng phương, cùng tần số tương ứng là (1), (2), (3). Dao động (1) ngược pha và có năng lượng gấp đôi dao động (2). Dao động tổng hợp (13) có năng lượng là 3W. Dao động tổng hợp (23) có năng lượng W và vuông pha với dao động (1). Dao động tổng hợp của vật có năng lượng gần nhất với giá trị nào sau đây?
A. 2,7 W. B. 3,3 W. C. 2,3 W. D. 1,7 W. |
Lời giải chi tiết:
| Phương pháp giản đồ vecto
${{E}_{1}}=2{{\text{E}}_{2}}\Rightarrow {{A}_{1}}=\sqrt{2}{{A}_{2}}$ ${{E}_{13}}=3{{\text{E}}_{23}}\Rightarrow {{A}_{13}}=\sqrt{3}\underbrace{{{A}_{23}}}_{X}$ Chuẩn hóa ${{A}_{2}}=1\Rightarrow {{A}_{1}}=\sqrt{2}$ Từ hình vẽ ta có ${{\left( \sqrt{3}X \right)}^{2}}={{X}^{2}}+{{\left( 1+\sqrt{2} \right)}^{2}}\Rightarrow X=\frac{1+\sqrt{2}}{\sqrt{2}}$ |
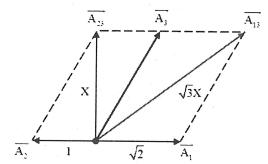 |
Vì ${{X}_{1}}\bot {{X}_{23}}$ nên biên độ dao động của dao động tổng hợp của vật này là
${{A}^{2}}=A_{23}^{2}+A_{1}^{2}={{\left( \frac{1+\sqrt{2}}{\sqrt{2}} \right)}^{2}}+{{\left( \sqrt{2} \right)}^{2}}$
Ta có $\frac{E}{{{E}_{23}}}=\frac{E}{\text{W}}=\frac{{{A}^{2}}}{A_{23}^{2}}=\frac{{{\left( \frac{1+\sqrt{2}}{\sqrt{2}} \right)}^{2}}+{{\left( \sqrt{2} \right)}^{2}}}{{{\left( \frac{1+\sqrt{2}}{\sqrt{2}} \right)}^{2}}}\approx 1,7$ . Chọn D.
| Bài tập 12: Hai dao động điều hòa, cùng phương, cùng tần số, biên độ dao động thứ nhất là ${{A}_{1}}=10$ cm. Khi ${{\text{x}}_{1}}=-5$cm thì li độ tổng hợp $\text{x}=-2$cm. Khi ${{\text{x}}_{2}}=0$ , thì $\text{x}=-5\sqrt{3}$cm. Độ lệch pha của dao động của hai dao động nhỏ hơn ${\pi }/{2}\;$ . Tính biên độ của dao động tổng hợp
A. 14 cm. B. 20 cm. C. $\frac{20}{\sqrt{3}}$ cm. D. $\frac{10}{\sqrt{3}}$ cm. |
Lời giải chi tiết:
Ta luôn có: $\text{x}={{x}_{1}}+{{x}_{2}}$ . Khi ${{\text{x}}_{2}}=0$ , thì $x={{x}_{1}}=-5\sqrt{3}$ cm $=-\frac{{{A}_{1}}\sqrt{3}}{2}$
Nghĩa là lúc này vecto $\overrightarrow{{{A}_{2}}}$ hợp với trục hoành một góc ${\pi }/{2}\;$ và vecto $\overrightarrow{{{A}_{1}}}$ hợp với chiều dương của trục hoành một góc ${5\pi }/{6}\;$ . Vậy ${{\text{x}}_{1}}$ sớm pha hơn ${{\text{x}}_{2}}$ là ${\pi }/{3}\;$ .
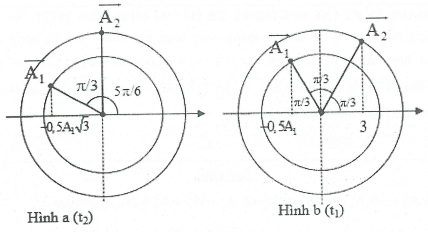
Khi ${{\text{x}}_{1}}=-5$ cm$=-\frac{{{A}_{1}}}{2}$ thì vecto $\overrightarrow{{{A}_{1}}}$ hợp với chiều dương của trục hoành một góc $2{\pi }/{3}\;$ và ${{\text{x}}_{2}}=x-{{x}_{1}}=-2-\left( -5 \right)=3$cm > 0. Lúc này, $\overrightarrow{{{A}_{2}}}$ hợp với chiều dương của trục hoành một góc ${\pi }/{3}\;$ nên ${{\text{x}}_{2}}={{A}_{2}}\cos \frac{\pi }{3}=3\Rightarrow {{A}_{2}}=6$ cm.
Biên độ dao động tổng hợp:
$A=\sqrt{A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \left( {{\varphi }_{1}}-{{\varphi }_{2}} \right)}=\sqrt{{{10}^{2}}+{{6}^{2}}+2.10.6.\cos \frac{\pi }{3}}=14$ cm. Chọn A.
| Bài tập 13: Hai chất điểm M và N có cùng khổi lượng, dao động điều hòa cùng tần số góc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox. Vị trí cân bằng của M và của N đều ở trên một đường thẳng qua gốc tọa độ và vuông góc với Ox. Biên độ của M là 6 cm, của N là 8 cm. Trong quá trình dao động, khoảng cách lớn nhất giữa M và N theo phương Ox là 10 cm. Mốc thế năng tại vị trí cân bằng. Ở thời điểm mà M có động năng bằng thế năng, tỉ số động năng của M và động năng của N là
A. $\frac{16}{9}$ . B. $\frac{9}{16}$ . C. $\frac{3}{4}$ . D. $\frac{4}{3}$ . |
Lời giải chi tiết:
| Khoảng cách giữa M và N là
$\Delta \text{x}=\left| {{x}_{M}}-{{x}_{N}} \right|=\left| 6\cos \left( \omega t+{{\varphi }_{1}} \right)-8\cos \left( \omega t+{{\varphi }_{2}} \right) \right|$ $=A\left| \cos \left( \omega t+\varphi \right) \right|$ Khoảng cách lớn nhất khi MN có phương nằm ngang $\Rightarrow {{6}^{2}}+{{8}^{2}}={{10}^{2}}\Rightarrow OM$ luôn vuông góc với ON. Ở thời điểm mà M có động năng bằng thế năng tại ${{\text{x}}_{M}}=A\frac{\sqrt{2}}{2}\left( {{\text{W}}_{dM}}={{\text{W}}_{tM}}=\frac{1}{2}{{\text{W}}_{M}} \right)$ tức OM hợp với Ox góc ${\pi }/{4}\;\Rightarrow ON$ hợp với Ox góc ${\pi }/{4}\;$ hay ${{\text{x}}_{N}}=-A\frac{\sqrt{2}}{2}$ $\Rightarrow {{\text{W}}_{dN}}={{\text{W}}_{tN}}=\frac{1}{2}{{\text{W}}_{N}}$ $\Rightarrow \frac{{{\text{W}}_{tM}}}{{{\text{w}}_{tN}}}=\frac{{{\text{W}}_{M}}}{{{\text{W}}_{N}}}=\frac{m{{\omega }^{2}}A_{M}^{2}}{m{{\omega }^{2}}A_{N}^{2}}={{\left( \frac{6}{8} \right)}^{2}}=\frac{9}{16}$ . Chọn D. |
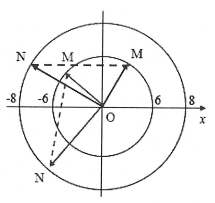 |
| Bài tập 14: [Đề thi thử THPT QG sở GD{}ĐT TP Hồ Chí Minh năm 2017]. Hai chất điểm dao động điều hòa cùng tần số, trên hai đường thẳng song song với nhau và song song với trục Ox có phương trình lần lượt là ${{\text{x}}_{1}}={{A}_{1}}\cos \left( \omega t+{{\varphi }_{1}} \right)$ và ${{\text{x}}_{2}}={{A}_{2}}\cos \left( \omega t+{{\varphi }_{2}} \right)$ . Giả sử $\text{x}={{x}_{1}}+{{x}_{2}}$ và $y={{x}_{1}}-{{x}_{2}}$ . Biết rằng biên độ dao động của x gấp 2 lần biên độ dao động của y. Độ lệch pha giữa ${{\text{x}}_{1}}$ và ${{\text{x}}_{2}}$ là $\Delta \varphi $. Giá trị nhỏ nhất của $\cos \Delta \varphi $ là
A. 0,5. B. 0,25. C. -1. D. 0,6. |
Lời giải chi tiết:
Ta có: $A_{x}^{2}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi =4A_{Y}^{2}$ và $A_{y}^{2}=A_{1}^{2}+A_{2}^{2}-2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi $ .
$\Rightarrow \left\{ \begin{array}{} 4{{A}_{1}}{{A}_{2}}\cos \Delta \varphi =3A_{y}^{2} \\ {} 5A_{y}^{2}=2\left( A_{1}^{2}+A_{2}^{2} \right) \\ \end{array} \right.\Rightarrow \cos \Delta \varphi
=\frac{3}{10}.\frac{A_{1}^{2}+A_{2}^{2}}{{{A}_{1}}{{A}_{2}}}\ge \frac{3}{10}.\frac{2{{A}_{1}}{{A}_{2}}}{{{A}_{1}}{{A}_{2}}}=0,6$ . Chọn C.
| Bài tập 15: [Trích đề thi THPT QG năm 2017]. Cho ${{D}_{1}},{{D}_{2}}$ và ${{\text{D}}_{3}}$ là ba dao động điều hòa cùng phương, cùng tần số. Dao động tổng hợp của ${{D}_{1}}$ và ${{\text{D}}_{2}}$ có phương trình là ${{\text{x}}_{12}}=3\sqrt{3}\cos \left( \omega t+\frac{\pi }{2} \right)$ cm. Dao động tổng hợp của ${{\text{D}}_{2}}$ và ${{\text{D}}_{3}}$ có phương trình ${{\text{x}}_{23}}=3\cos \left( \omega t \right)$ (cm). Dao động ${{D}_{1}}$ ngược pha với dao động ${{D}_{3}}$ . Biên độ dao động ${{\text{D}}_{2}}$ có giá trị nhỏ nhất là
A. 2,6 cm. B. 2,7 cm. C. 3,6 cm. D. 3,7 cm. |
Lời giải chi tiết:
Ta có: ${{\text{x}}_{1}}+{{x}_{2}}={{x}_{12}}=3\sqrt{3}\cos \left( \omega t+\frac{\pi }{2} \right)$ và ${{\text{x}}_{2}}+{{x}_{3}}={{x}_{23}}=3\cos \left( \omega t \right)$ .
Suy ra ${{\text{x}}_{1}}-{{x}_{3}}=3\sqrt{3}\angle \frac{\pi }{2}-3\angle 0=6\angle \frac{2}{3}\pi $ .
Do dao động ${{\text{D}}_{1}}$ ngược pha với dao động ${{D}_{3}}$ nên ${{\text{x}}_{3}}=-k\text{x}\Rightarrow {{x}_{1}}=\frac{6}{k+1}\angle \frac{2\pi }{3}\left( k>0 \right)$
Do đó ${{\text{x}}_{2}}=3\sqrt{3}\angle \frac{\pi }{2}-\frac{6}{k+1}\angle \frac{2\pi }{3}\left( k>0 \right)$
Suy ra $A_{2}^{2}={{\left( 3\sqrt{3} \right)}^{2}}+{{\left( \frac{6}{k+1} \right)}^{2}}-2.3\sqrt{3}.\frac{6}{k+1}\cos \frac{\pi }{6}=27+{{t}^{2}}-9t\left( t=\frac{6}{k+1} \right)$
Vậy $A_{2}^{2}={{\left( t-\frac{9}{2} \right)}^{2}}+\frac{27}{4}\ge \frac{27}{4}\Rightarrow {{A}_{2}}\ge \frac{3\sqrt{3}}{2}=2,6$ cm
Dấu bằng xảy ra khi $\frac{6}{k+1}=\frac{9}{2}\Leftrightarrow k=\frac{1}{3}\left( tm \right)$ .Chọn A.
| Bài tập 16: Một chất điểm tham gia đồng thời hai dao động cùng phương. Phương trình ly độ của các dao động thành phần và dao động tổng hợp lần lượt là ${{\text{x}}_{1}}={{A}_{1}}\cos \left( \omega t \right)$ cm; ${{x}_{2}}=3\cos \left( \omega t+\alpha \right)$ cm; và $\text{x}=A\cos \left( \omega t+{\pi }/{6}\; \right)$ cm. Biên độ dao động ${{A}_{1}}$ có giá trị lớn nhất là
A. 9 cm. B. 6 cm. C. 8 cm. D. 12 cm. |
Lời giải chi tiết:
| Định lý hàm số sin trong tam giác $OA{{A}_{1}}$ :
$\frac{3}{\sin 30{}^\circ }=\frac{{{A}_{1}}}{\sin \left( \alpha -30{}^\circ \right)}$ $\Rightarrow {{A}_{1}}=6\sin \left( \alpha -30{}^\circ \right)\le 6\Rightarrow {{A}_{1\max }}=6$ cm. Chọn B. |
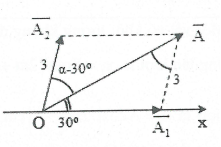 |
| Bài tập 17: Một chất điểm tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số, có phương trình ${{\text{x}}_{1}}={{A}_{1}}\cos \left( \omega t-{\pi }/{3}\; \right)$ và ${{\text{x}}_{2}}={{A}_{2}}\cos \left( \omega t+{\pi }/{3}\; \right)$ . Dao động tổng hợp có biên độ $4\sqrt{3}$ cm. Khi ${{A}_{1}}$ đạt giá trị cực đại thì ${{A}_{2}}$ có giá trị là
A. 2 cm. B. 3 cm. C. 5 cm. D. 4 cm. |
Lời giải chi tiết:
| Độ lệch pha $\Delta \varphi ={\pi }/{3}\;-\left( {-\pi }/{3}\; \right)={2\pi }/{3}\;$ .
Áp dụng định lí hàm số sin trong tam giác $OA{{A}_{1}}$ : $\frac{4\sqrt{3}}{\sin 60{}^\circ }=\frac{{{A}_{1}}}{\sin \alpha }\Rightarrow {{A}_{1}}=8\sin \alpha \le 8$ ${{A}_{1\max }}=8$ khi $\alpha =90{}^\circ \Rightarrow {{A}_{2}}=\sqrt{64-48}=4$ cm. Chọn D. |
<img src=””https://myfiles.space/user_files/45335_ |
