BÀI TẬP CON LẮC ĐƠN (CLĐ) TRONG ĐIỆN TRƯỜNG CÓ ĐÁP ÁN CHI TIẾT
Bài tập 1: [Trích đề thi tuyển sinh Đại học 2010]. Một con lắc đơn có chiều dài dây treo
$\ell $= 50 cm và vật nhỏ có khối lượng m = 0,01 (kg) mang điện tích q= ${{5.10}^{-6}}$ C, được coi là điện tích điểm. Con lắc dao động điều hòa trong điện trường đều mà véc tơ cường độ điện trường có độ lớn $E={{10}^{4}}(V/m)$ và hướng thẳng đứng xuống dưới. Lấy $g=10m/{{s}^{2}}$, $\pi $= 3,14. Tính chu kỳ dao động điều hòa của con lắc.
A. 0,58s B. 1,4s C. 1,15s D. 1,99s
Lời giải chi tiết:
Cách 1: Do $\overrightarrow{E}\downarrow $, q>0 nên $\overrightarrow{F}\downarrow $ $\to P’=P+F\Leftrightarrow g’=g+\frac{\left| q \right|E}{m}$=10+5=15 ($m/{{s}^{2}}$)
Chu kỳ dao động của con lắc $T’=2\pi \sqrt{\frac{\ell }{g’}}=2\pi \sqrt{\frac{1}{15}}\approx 1,15(s)$. Chọn C.
Cách 2: Ta có thể làm như sau: Do $\overrightarrow{E}\downarrow $ ( cùng chiều với trọng lực ) nên
$g’=g+\frac{qE}{m}=15(m/{{s}^{2}})$ suy ra $T’=2\pi \sqrt{\frac{\ell }{g’}}=2\pi \sqrt{\frac{1}{15}}\approx 1,15(s)$. Chọn C.
Bài tập 2: Một con lắc đơn có chiều dài dây treo $\ell $ = 50 cm và vật nhỏ có khối lượng 50g mang điện tích q= $-1,{{2.10}^{-4}}$ C được coi là điện tích điểm. Con lắc dao động điều hòa trong điện trường đều mà véc tơ cường độ điện trường có độ lớn E=40V/cm và hướng thẳng đứng lên trên, tại nơi có gia tốc trọng trường $g=9,8(m/{{s}^{2}})$. Chu kỳ dao động điều hòa của con lắc là:
A. T=1,2s B. T=1s C. 1,1s D. T=0,5s
Lời giải chi tiết:
Do $\overrightarrow{E}\uparrow $ ( ngược chiều với trọng lực ) nên $g’=g-\frac{qE}{m}=9,8-\frac{(-1,{{2.10}^{-4}}).4000}{0,05}$
Suy ra $g’=19,4(m/{{s}^{2}})$
Do đó chu kỳ dao động điều hòa của con lắc là: $T’=2\pi \sqrt{\frac{\ell }{g’}}=1(s)$ Chọn B.
Bài tập 3: Một con lắc đơn treo hòn bi kim loại khối lượng m=200g mang điện tích
q= $2,{{5.10}^{-7}}$C. Đặt con lắc trong điện trường đều $\overrightarrow{E}$ có phương thẳng đứng hướng xuống dưới.
Chu kỳ con lắc khi E=0 là T=3s. Tìm chu kỳ dao động khi E= ${{10}^{5}}$(V/m) và $g=10(m/{{s}^{2}})$
A. T’=2,8s B. T’=3,2s C. T’=3,02s D. T’=2,98s
Lời giải chi tiết:
Cách 1: Ta có: q > 0 nên $\overrightarrow{E}$ cùng chiều với lực điện $\overrightarrow{{{F}_{d}}}$
Mà $\overrightarrow{E}\downarrow \Rightarrow \overrightarrow{F}\downarrow \Rightarrow g’=g+\frac{\left| q \right|E}{m}\Rightarrow \frac{T}{T’}=\sqrt{\frac{g’}{g}}=\sqrt{\frac{g+\frac{\left| q \right|E}{m}}{g}}=\sqrt{1+\frac{\left| q \right|E}{mg}}$
Khi đó $T’=\frac{T}{\sqrt{1+\frac{\left| q \right|E}{mg}}}=$2,98s. Chọn D.
Cách 2: Do $\overrightarrow{E}$ hướng xuống nên $g’=g+\frac{qE}{m}$. Chọn D.
Bài tập 4: Con lắc đơn dao động điều hòa với chu kỳ T. Sau đó người ta tích điện cho vật nặng một điện tích q rồi truyền cho con lắc dao động trong một điện trường đều có véc tơ cường độ điện trường $\overrightarrow{E}$ hướng thẳng đứng lên trên thì thấy chu kỳ dao động của con lắc khi đó là $T’=\frac{T}{\sqrt{3}}$. Cho E= ${{4.10}^{5}}$ V/m, g=10 $(m/{{s}^{2}})$, khối lượng vật nặng m=50g . Điện tích của vật này là
A. q=2,5 μC B. q=-5 μC C. q=-2,5 μC D. q=5 μC
Lời giải chi tiết:
Từ giả thiết $T’=\frac{T}{\sqrt{3}}\Leftrightarrow \frac{T’}{T}=\frac{1}{\sqrt{3}}\Leftrightarrow \frac{T’}{T}=\sqrt{\frac{g}{g’}}=\frac{1}{\sqrt{3}}\Leftrightarrow g’=3g$
Do $\overrightarrow{E}$hướng thẳng đứng lên trên ( ngược chiều với trọng lực ) nên:
$g’=g-\frac{qE}{m}\Leftrightarrow 2g=\frac{-qE}{m}\Rightarrow q=-2,{{5.10}^{-6}}C=-2,5$μC. Chọn C.
Bài tập 5: Một con lắc đơn dao động bé có chu kỳ T. Đặt con lắc trong điện trường đều có phương thẳng đứng hướng xuống dưới. Khi quả cầu của con lắc tích điện ${{q}_{1}}$thì chu kỳ của con lắc là ${{T}_{1}}=4T$. Khi quả cầu của con lắc tích điện ${{q}_{2}}$ thì chu kỳ ${{T}_{2}}=\frac{2}{3}T$ . Tỉ số giữa hai điện tích $\frac{{{q}_{1}}}{{{q}_{2}}}$là
A. $\frac{{{q}_{1}}}{{{q}_{2}}}=-\frac{3}{4}$ B. $\frac{{{q}_{1}}}{{{q}_{2}}}=\frac{3}{4}$ C. $\frac{{{q}_{1}}}{{{q}_{2}}}=-1$ D. $\frac{{{q}_{1}}}{{{q}_{2}}}=1$
Lời giải chi tiết:
Do vecto cường độ điện trường hướng xuống nên ta có: $g’=g+\frac{qE}{m}$
Ta có: $\frac{{{T}_{1}}}{T}=\sqrt{\frac{g}{{{g}_{1}}}}=\sqrt{\frac{g}{g+\frac{{{q}_{1}}E}{m}}}\Rightarrow \frac{{{T}^{2}}}{{{T}_{1}}^{2}}=1+\frac{{{q}_{1}}E}{mg}$
Tương tự ta có: $\frac{{{T}^{2}}}{{{T}_{2}}^{2}}=1+\frac{{{q}_{2}}E}{mg}$. Do đó $\frac{{{q}_{1}}}{{{q}_{2}}}=\left( \frac{\frac{{{T}^{2}}}{{{T}_{1}}^{2}}-1}{\frac{{{T}^{2}}}{{{T}_{2}}^{2}}-1} \right)=\frac{-3}{4}$. Chọn A.
Bài tập 6: Một con lắc đơn dao động điều hòa trong điện trường đều, có véc tơ cường độ điện trường có phương thẳng đứng, hướng xuống. Khi vật treo chưa tích điện thì chu kỳ dao động là T=0,4s khi vật treo lần lượt tích điện ${{q}_{1}}$ và ${{q}_{2}}$ thì chu kỳ dao động tương ứng là ${{T}_{1}}$=0,25s và ${{T}_{2}}$=0,5s. Tỉ số $\frac{{{q}_{1}}}{{{q}_{2}}}$ là
A. $\frac{{{q}_{1}}}{{{q}_{2}}}=\frac{-8}{13}$ B. $\frac{{{q}_{1}}}{{{q}_{2}}}=\frac{-13}{3}$ C. $\frac{{{q}_{1}}}{{{q}_{2}}}=\frac{-13}{8}$ D. $\frac{{{q}_{1}}}{{{q}_{2}}}=\frac{13}{8}$
Lời giải chi tiết:
Tương tự ví dụ trên ta có: $\begin{array}{} \frac{{{q}_{1}}}{{{q}_{2}}}=\frac{\left( \frac{{{T}^{2}}}{{{T}_{1}}^{2}}-1 \right)}{\left( \frac{{{T}^{2}}}{{{T}_{2}}^{2}}-1 \right)}=\frac{-13}{3} \\ {} \\ \end{array}$. Chọn B.
Bài tập 7: Hai con lắc đơn cùng chiều dài và cùng khối lượng, các vật nặng coi là chất điểm, chúng được đặt ở cùng một nơi và trong điện trường đều $\overrightarrow{E}$có phương thẳng đứng hướng xuống, gọi ${{T}_{0}}$là chu kỳ chưa tích điện của mỗi con lắc, các vật nặng được tích điện là ${{q}_{1}}$ và ${{q}_{2}}$ thì chu kỳ trong điện trường tương ứng là ${{T}_{1}}$ và ${{T}_{2}}$, biết ${{T}_{1}}=0,8{{T}_{0}}$ và ${{T}_{2}}=1,2{{T}_{0}}$. Tỉ số $\frac{{{q}_{1}}}{{{q}_{2}}}$ là
A. $\frac{44}{81}$ B. $\frac{-81}{44}$ C. $\frac{-44}{81}$ D. $\frac{81}{44}$
Lời giải chi tiết:
Tương tự ví dụ trên ta có: $\frac{{{q}_{1}}}{{{q}_{2}}}=\frac{\left( \frac{{{T}_{0}}^{2}}{{{T}_{1}}^{2}}-1 \right)}{\left( \frac{{{T}_{0}}^{2}}{{{T}_{2}}^{2}}-1 \right)}=\frac{-81}{44}$. Chọn B.
Bài tập 8: Một con lắc đơn dao động điều hòa trong điện trường đều, có véc tơ cường độ điện trường có phương thẳng đứng, hướng xuống. Khi vật treo chưa tích điện thì chu kỳ dao động là T, khi vật treo lần lượt tích điện là q và –q thì chu kỳ dao động tương ứng là ${{T}_{1}}$=1,05s và ${{T}_{2}}$ = 0,15s . Giá trị của T là:
A. T=0,14s B. T=0,07s C.T=0,21s D. T=0,28s
Lời giải chi tiết:
Áp dụng công thức $\frac{{{q}_{1}}}{{{q}_{2}}}=\frac{\left( \frac{{{T}^{2}}}{{{T}_{1}}^{2}}-1 \right)}{\left( \frac{{{T}^{2}}}{{{T}_{2}}^{2}}-1 \right)}=-1\Rightarrow \frac{{{T}^{2}}}{1,{{05}^{2}}}-1=1-\frac{{{T}^{2}}}{0,{{15}^{2}}}\Rightarrow {{T}^{2}}=\frac{2}{\frac{1}{1,{{05}^{2}}}+\frac{1}{0,{{15}^{2}}}}$
Do đó T=0,21s. Chọn C.
Bài tập 9: Có ba con lắc đơn cùng chiều dài dây treo và cùng khối lượng. Con lắc thứ nhất và thứ hai mang điện tích ${{q}_{1}}$và ${{q}_{2}}$. Con lắc thứ ba không điện tích. Đặt lần lượt ba con lắc vào điện trường đều có véc tơ cường độ điện trường theo phương thẳng đứng và hướng xuống. Chu kỳ dao động điều hòa của chúng trong điện trường lần lượt là ${{T}_{1}}$, ${{T}_{2}}$ và ${{T}_{3}}$ với ${{T}_{1}}=\frac{{{T}_{3}}}{3}$, ${{T}_{2}}=\frac{{{T}_{3}}}{\sqrt{3}}$. Cho biết${{q}_{1}}+{{q}_{2}}={{10}^{-5}}C$ . Điện tích ${{q}_{1}}$ và ${{q}_{2}}$ có giá trị lần lượt là:
A.${{q}_{1}}={{8.10}^{-6}}C$ ; ${{q}_{2}}={{2.10}^{-6}}C$ B. ${{q}_{1}}={{6.10}^{-6}}C$ ; ${{q}_{2}}={{4.10}^{-6}}C$
C. ${{q}_{1}}={{12.10}^{-6}}C$; ${{q}_{2}}=-{{2.10}^{-6}}C$ D. ${{q}_{1}}=13,{{33.10}^{-6}}C$; ${{q}_{2}}=-3,{{33.10}^{-6}}C$
Lời giải chi tiết:
Áp dụng công thức bài trên với $T={{T}_{3}}$ ta có: $\frac{{{q}_{1}}}{{{q}_{2}}}=\frac{\left( \frac{{{T}^{2}}}{{{T}_{1}}^{2}}-1 \right)}{\left( \frac{{{T}^{2}}}{{{T}_{2}}^{2}}-1 \right)}=4\Rightarrow \left\{ \begin{array}{} {{q}_{1}}={{8.10}^{-6}}C \\ {} {{q}_{2}}={{2.10}^{-6}}C \\ \end{array} \right.$. Chọn A.
Bài tập 10: Một con lắc đơn mang điện, khi không có điện trường nó dao động với chu kỳ T. Khi có điện trường hướng thẳng đứng xuống thì chu kỳ dao động điều hòa của con lắc là ${{T}_{1}}$. Khi có điện trường hướng thẳng đứng lên thì chu kỳ dao động điều hòa của con lắc là ${{T}_{2}}$. Hệ thức nào sau đây là đúng
A. $\frac{1}{{{T}^{2}}}=\frac{1}{{{T}_{1}}^{2}}+\frac{1}{{{T}_{2}}^{2}}$ B. $\frac{2}{{{T}^{2}}}=\frac{1}{{{T}_{1}}^{2}}+\frac{1}{{{T}_{2}}^{2}}$ C. ${{T}^{2}}={{T}_{1}}^{2}+{{T}_{2}}^{2}$ D. $\frac{1}{2{{T}^{2}}}=\frac{1}{{{T}_{1}}^{2}}+\frac{1}{{{T}_{2}}^{2}}$
Lời giải chi tiết:
Khi $\overrightarrow{E}\downarrow \Rightarrow {{g}_{1}}=g+\frac{qE}{m}\Leftrightarrow \frac{1}{{{T}_{1}}^{2}}=\frac{1}{4{{\pi }^{2}}}\left( \frac{g+\frac{qE}{m}}{\ell } \right)=\frac{1}{4{{\pi }^{2}}\ell }\left( g+\frac{qE}{m} \right)$
Khi $\overrightarrow{E}\uparrow $ tương tự ta có: ${{g}_{2}}=g-\frac{qE}{m}\Leftrightarrow \frac{1}{{{T}_{2}}^{2}}=\frac{1}{4{{\pi }^{2}}\ell }\left( g-\frac{qE}{m} \right)$
Mặt khác $\frac{1}{{{T}_{2}}}=\frac{1}{4{{\pi }^{2}}}.\frac{g}{\ell }=\frac{1}{2}\left( \frac{1}{{{T}_{1}}^{2}}+\frac{1}{{{T}_{2}}^{2}} \right)$. Do đó $\frac{2}{{{T}^{2}}}=\frac{1}{{{T}_{1}}^{2}}+\frac{1}{{{T}_{2}}^{2}}$. Chọn B.
Bài tập 11: Một con lắc đơn gồm một quả cầu kim loại, khối lượng m=50g, tích điện q=${{4.10}^{-6}}C$ được treo bằng sợi dây mảnh. Con lắc dao động trong điện trường đều có phương ngang tại nơi có gia tốc trọng trường $g=10m/{{s}^{2}}$. Khi đó vị trí cân bằng của con lắc tạo với phương thẳng đứng một góc $\alpha =30{}^\circ $. Độ lớn của cường độ điện trường là:
A.E= ${{21.10}^{4}}$ V/m B. E= $7,{{2.10}^{4}}$ V/m C. E=$12,{{5.10}^{4}}$ V/m D. E=${{25.10}^{4}}$ V/m
Lời giải chi tiết:
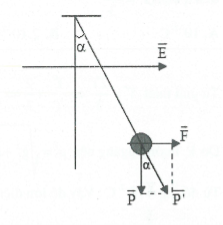
$\overrightarrow{E}$ có phương ngang, khi đó $\overrightarrow{F}$cũng có phương ngang. Do trọng lực P hướng xuống nên $\overrightarrow{F}\bot \overrightarrow{P}$
Ta có: F=qE, P=mg.
Góc lệch của con lắc so với phương ngang là $\alpha $ được xác định bởi công thức: $\tan \alpha =\frac{F}{P}=\frac{\left| q \right|E}{mg}=\tan 30{}^\circ \Rightarrow E=\frac{mg\tan 30{}^\circ }{\left| q \right|}$
=$7,{{2.10}^{4}}$ V/m. Chọn B.
Bài tập 12: Một con lắc đơn dây treo có chiều dài $\ell $= 50cm, quả cầu có khối lượng m=200g, được tích điện q= ${{2.10}^{-6}}$C đặt trong điện trường đều $\overrightarrow{E}$ có phương ngang và độ lớn ${{10}^{6}}$ V/m. Lấy $g=10m/{{s}^{2}}$. Kéo con lắc sang phải và lệch so với phương thẳng đứng một góc $60{}^\circ $ rồi thả nhẹ. Tính tốc độ của vật khi sợi dây sang phải và lệch so với phương thẳng đứng góc $42{}^\circ $ A.0,81m/s B.0,96m/s C.2,2m/s D.2,62m/s
Lời giải chi tiết:
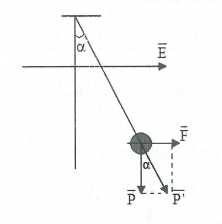
$\overrightarrow{E}$ có phương ngang, khi đó $\overrightarrow{F}$ cũng có phương ngang.
Do trọng lực P hướng xuống nên $\overrightarrow{F}\bot \overrightarrow{P}$.
Từ đó, $P{{‘}^{2}}={{P}^{2}}+{{F}^{2}}\Leftrightarrow {{(mg’)}^{2}}={{(mg)}^{2}}+{{(\left| q \right|E)}^{2}}$
$\Rightarrow g’=\sqrt{{{g}^{2}}+{{\left( \frac{qE}{m} \right)}^{2}}}=10\sqrt{2}\Rightarrow \left( \widehat{\overrightarrow{g’};\overrightarrow{g}} \right)={{\alpha }_{cb}}=45{}^\circ $
Do đó ${{\alpha }_{\max }}=60{}^\circ -45{}^\circ =15{}^\circ $.
Khi con lắc lệch với phương thẳng đứng góc $42{}^\circ \Rightarrow \alpha =45{}^\circ -42{}^\circ =3{}^\circ $ $v=\sqrt{2g’\ell (\cos \alpha -cos{{\alpha }_{\max }})}=\sqrt{2g’\ell (\cos 3{}^\circ -cos15{}^\circ )}=0,96m/s$. Chọn B.
Bài tập 13:Một con lắc đơn có khối lượng vật nặng m=20g, đặt trong điện trường đều $\overrightarrow{E}$ có phương ngang và độ lớn E= ${{4.10}^{5}}$ (V/m). Khi vật chưa tích điện nó dao động với chu kỳ T, khi vật được tích điện tích q thì nó dao động với chu kỳ T’. Lấy $g=10(m/{{s}^{2}})$, xác định độ lớn của điện tích q biết $T’=\frac{2T}{3}$
A. ${{10}^{-7}}$ C B. ${{2.10}^{-7}}$C C. ${{4.10}^{-7}}$C D. ${{10}^{-8}}$C
Lời giải chi tiết:
Từ giả thiết $T’=\frac{2T}{3}\Leftrightarrow \frac{T’}{T}=\frac{2}{3}\Leftrightarrow \sqrt{\frac{g}{g’}}=\frac{2}{3}\Leftrightarrow g’=\frac{9}{4}g$
Do $\overrightarrow{E}$ hướng ngang nên $g’=\sqrt{{{g}^{2}}+{{\left( \frac{\left| q \right|E}{m} \right)}^{2}}}\Leftrightarrow {{\left( \frac{9}{4}g \right)}^{2}}={{g}^{2}}+{{\left( \frac{\left| q \right|E}{m} \right)}^{2}}\Leftrightarrow {{\left( \frac{qE}{m} \right)}^{2}}=\frac{65}{16}$
Từ đó, $\left| q \right|={{10}^{-7}}C$. Vậy độ lớn điện tích của q là ${{10}^{-7}}$C. Chọn A.
Bài tập 14: [Trích đề thi đại học năm 2012] Một con lắc đơn gồm dây treo có chiều dài 1m và vật nhỏ có khối lượng 100g, mang điện tích ${{2.10}^{-5}}$C. Treo con lắc đơn này trong điện trường đều với véc tơ cường độ điện trường hướng theo phương ngang và có độ lớn ${{5.10}^{4}}$ V/m. Trong mặt phẳng thẳng đứng đi qua điểm treo và song song với véc tơ cường độ điện trường, kéo vật nhỏ theo chiều của véc tơ cường độ điện trường sao cho dây treo hợp với véc tơ gia tốc trọng trường một góc $54{}^\circ $ rồi buông nhẹ cho con lắc dao động điều hòa. Lấy $g=10m/{{s}^{2}}$. Trong quá trình dao động, giá trị cực đại của vật nhỏ là:
A. 0,59 m/s B.3,14 m/s C. 2,87 m/s D.0,5 m/s
Lời giải chi tiết:
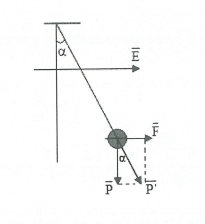
$\overrightarrow{E}$ có phương ngang, khi đó $\overrightarrow{F}$ cũng có phương ngang.
Do trọng lực P hướng xuống nên $\overrightarrow{F}\bot \overrightarrow{P}$.
Từ đó, $P{{‘}^{2}}={{P}^{2}}+{{F}^{2}}\Leftrightarrow {{(mg’)}^{2}}={{(mg)}^{2}}+{{(\left| q \right|E)}^{2}}$
$\Rightarrow g’=\sqrt{{{g}^{2}}+{{\left( \frac{\left| q \right|E}{m} \right)}^{2}}}=10\sqrt{2}\Rightarrow \left( \widehat{\overrightarrow{g’};\overrightarrow{g}} \right)=45{}^\circ $
Do đó${{\alpha }_{\max }}=54{}^\circ -45{}^\circ =9{}^\circ $. Khi đó
${{v}_{\max }}=\sqrt{2g’\ell (1-cos{{\alpha }_{\max }})}=\sqrt{2g’.\ell .(1-cos9{}^\circ )}=0,59m/s$. Chọn A.
Bài tập 15: [Trích đề thi Chuyên Hạ Long-Quảng Ninh] Một con lắc đơn gồm một vật nhỏ khối lượng m=2g và một dây treo mảnh, chiều dài $\ell $, được kích thích cho dao động điều hòa. Trong khoảng thời gian $\vartriangle t$ con lắc thực hiện được 40 dao động. Khi tăng chiều dài con lắc thêm một đoạn 7,9 cm thì cũng trong khoảng thời gian $\vartriangle t$ con lắc thực hiện được 39 dao động. Lấy gia tốc trọng trường $g=9,8m/{{s}^{2}}$. Để con lắc với chiều dài tăng thêm có cùng chu kỳ dao động với con lắc chiều dài$\ell $, người ta truyền cho vật điện tích q= $+0,{{5.10}^{-8}}$ C rồi cho nó dao động điều hòa trong một điện trường đều có đường sức thẳng đứng. Vecto cường độ điện trường này có:
A.Chiều hướng lên và độ lớn $1,{{02.10}^{5}}V/m$
B.Chiều hướng xuống và độ lớn $1,{{02.10}^{5}}V/m$
C. Chiều hướng lên và độ lớn $2,{{04.10}^{5}}V/m$
D.Chiều hướng xuống và độ lớn $2,{{04.10}^{5}}V/m$
Lời giải chi tiết:
Ta có: ${{T}_{1}}=\frac{\vartriangle t}{40}=2\pi \sqrt{\frac{\ell }{g}},{{T}_{2}}=\frac{\vartriangle t}{39}=2\pi \sqrt{\frac{\ell +0,079}{g}}$
Suy ra $\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{39}{40}=\sqrt{\frac{\ell }{\ell +0,079}}$
Lại có: ${{T}_{dt}}=2\pi \sqrt{\frac{\ell +0,079}{g+\frac{qE}{m}}}={{T}_{1}}=2\pi \sqrt{\frac{\ell }{g}}\Leftrightarrow \sqrt{\frac{\ell +0,079}{\ell }}=\sqrt{\frac{g+\frac{qE}{m}}{g}}$
$\Leftrightarrow {{\left( \frac{40}{39} \right)}^{2}}=1+\frac{qE}{mg}\Rightarrow E=+2,{{04.10}^{5}}$
Do đó E có chiều hướng xuống và độ lớn $2,{{04.10}^{5}}$ V/m. Chọn D.
Bài tập 16: [Chuyên ĐHSP lần 1 năm 2017] Con lắc đơn có khối lượng m=100g treo vào một điểm cố định trong điện trường đều có phương thẳng đứng, hướng lên trên E= ${{2.10}^{6}}$ V/m. Khi chưa tích điện, con lắc vật dao động điều hòa với chu kỳ ${{T}_{0}}$=2s. Khi tích điện q cho con lắc, nó dao động điều hòa với chu kỳ giảm đi 4/3 lần. Lấy g=10$m/{{s}^{2}}$. Điện tích của vật là:
A. q= $3,{{89.10}^{-7}}$C B.q= $-3,{{89.10}^{-7}}$C C. q= $3,{{89.10}^{-6}}$C D.q= $-3,{{89.10}^{-6}}$C
Lời giải chi tiết:
Do$\overrightarrow{E}\uparrow $ nên ngược chiều với g suy ra $g’=g-\frac{qE}{m}$
Ta có: $T’=\frac{3}{4}{{T}_{0}}\Rightarrow 2\pi \sqrt{\frac{\ell }{g-\frac{qE}{m}}}=2\pi \sqrt{\frac{\ell }{g}}.\frac{3}{4}$
$\Leftrightarrow \frac{g-\frac{qE}{m}}{g}=\frac{16}{9}\Leftrightarrow \frac{qE}{mg}=\frac{-7}{9}\Rightarrow q=-3,{{89.10}^{-7}}$. Chọn B.
Bài tập 17: Một hòn bi nhỏ khối lượng m treo ở đầu một sợi dây và dao động nhỏ tại nơi có gia tốc trọng trường g. Chu kỳ dao động thay đổi bao nhiêu lần nếu hòn bi được tích một điện tích q >0 và đặt trong một điện trường đều có véc tơ cường độ E thẳng đứng hướng xuống dưới sao cho qE=8mg.
A.tăng 5 lần B. giảm 5 lần C. tăng 3 lần D. giảm 3 lần
Lời giải chi tiết:
Gia tốc trọng trường hiệu dụng$g’=g+\frac{qE}{m}=g+8g=9g$
Ta có ${{\left( \frac{T’}{T} \right)}^{2}}=\frac{g}{g’}\Leftrightarro
