VẤN ĐỀ 3: KÍNH LÚP
LÝ THUYẾT CHUNG
– Kính lúp là dụng cụ quang học bổ trợ cho mắt trong việc quan sát các vật nhỏ bằng cách tạo ra một ảnh ảo cùng chiều lớn hơn vật và nằm trong giới hạn nhìn rõ của mắt. Kính lúp đơn giản nhất là một thấu kính hội tụ tiêu cự ngắn (cỡ vài cm).
– Cách ngắm chừng: Đặt vật AB trước kính, trong khoảng tiêu cự của kính để có một ảnh ảo A’B’ cùng chiều và lớn hơn vật. Mắt đặt sau kính để quan sát ảnh ảo này. Cần điều chỉnh vị trí vật hay vị trí kính để ảnh ảo này nằm trong giới hạn nhìn rõ của mắt.
+) Nếu điều chỉnh để ảnh ở Cc, ta có ngắm chừng ở điểm cực cận.
+) Nếu điều chỉnh để ảnh ở Cv, ta có ngắm chừng ở điểm cực viễn.
+) Nếu điều chỉnh để ảnh ở vô cực, ta có ngắm chừng ở vô cực.
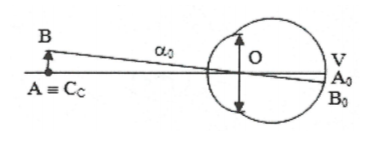– Số (độ) bội giác của kính lúp: là tỉ số giữa góc trông ảnh ( 
) qua dụng cụ và góc trông vật ( 0) trực tiếp bằng mắt khi đặt vật ở điểm cực cận:
$\text{G}=\frac{\alpha }{{{\alpha }_{0}}}=\frac{\tan \alpha }{\tan {{\alpha }_{0}}}$
Từ hình vẽ ta có: $\tan {{\alpha }_{0}}=\frac{\text{AB}}{\text{O}{{\text{C}}_{\text{c}}}}$
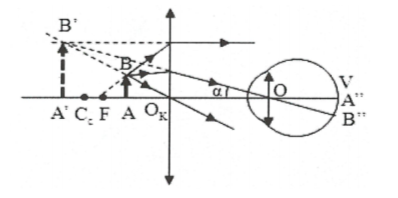
Từ hình vẽ ta có:
$\tan \alpha =\frac{\text{A }\!\!’\!\!\text{ B }\!\!’\!\!\text{ }}{\text{OA }\!\!’\!\!\text{ }}=\frac{\text{A }\!\!’\!\!\text{ B }\!\!’\!\!\text{ }}{\text{O}{{\text{O}}_{\text{k}}}\text{+}{{\text{O}}_{\text{k}}}\text{A }\!\!’\!\!\text{ }}=\frac{\text{A }\!\!’\!\!\text{ B }\!\!’\!\!\text{ }}{\ell +\left| \text{d }\!\!’\!\!\text{ } \right|}$
$\Rightarrow \text{G}=\frac{\text{A }\!\!’\!\!\text{ B }\!\!’\!\!\text{ }}{\text{AB}}\left( \frac{\text{O}{{\text{C}}_{\text{c}}}}{\ell +\left| \text{d }\!\!’\!\!\text{ } \right|} \right)=\text{k}\left( \frac{\text{O}{{\text{C}}_{\text{c}}}}{\ell +\left| \text{d }\!\!’\!\!\text{ } \right|} \right)$
+) Ngắm chừng ở cực cận thì:
$\text{OA }\!\!’\!\!\text{ }=\text{O}{{\text{C}}_{\text{c}}}=\text{d }\!\!’\!\!\text{ }+\ell \Rightarrow {{\text{G}}_{\text{c}}}=\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}}={{\text{k}}_{\text{c}}}$
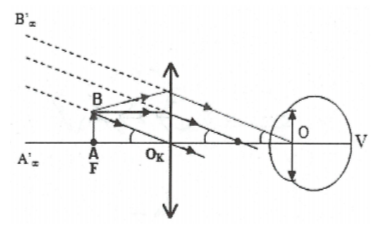
+) Ngắm chừng ở điểm cực viễn thì:
$\text{OA }\!\!’\!\!\text{ }=\text{O}{{\text{C}}_{\text{v}}}=\text{d }\!\!’\!\!\text{ }+\ell \Rightarrow
{{\text{G}}_{\text{v}}}={{\text{k}}_{\text{v}}}\text{.}\frac{\text{O}{{\text{C}}_{\text{c}}}}{\text{O}{{\text{C}}_{\text{v}}}}$
+) Ngắm chừng ở vô cực:
$\tan \alpha =\frac{\text{AB}}{\text{f}}\Rightarrow {{\text{G}}_{\infty }}=\frac{\text{O}{{\text{C}}_{\text{c}}}}{\text{f}}=\frac{{{\text{}}_{\text{c}}}}{\text{f}}$
Khi trên kính lúp ghi là 8x thì ta hiểu:
$\text{G}=8=\frac{0,25}{\text{f}}$ (f đo bằng m)
BÀI TẬP VỀ KÍNH LÚP
|
Bài tập 1: Một kính lúp là thấu kính hội tụ có độ tụ +10 dp. a) Tính độ bội giác của kính khi ngắm chừng ở vô cực. b) Tính độ bội giác của kính và độ phóng đại của ảnh khi người quan sát ngắm chừng ở điểm cực cận. Cho biết OCc = 25 cm. Mắt đặt sát kính. |
Lời giải chi tiết:
a) Tiêu cự của kính lúp: $\text{f}=\frac{\text{1}}{\text{D}}=\frac{1}{10}=0,1\text{m}=10\text{cm}.$
Độ bội giác khi ngắm chừng ở vô cực: ${{\text{G}}_{\infty }}=\frac{\text{}}{\text{f}}=\frac{\text{O}{{\text{C}}_{\text{c}}}}{\text{f}}=\frac{25}{10}=2,5.$
b) Khi ngắm chừng ở điểm cực cận thì vật qua kính cho ảnh ảo ở Cc. Sơ đồ tạo ảnh (hình vẽ):
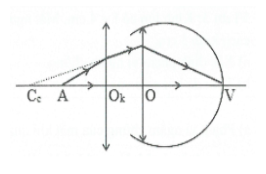$\text{A}\xrightarrow{{{\text{O}}_{\text{k}}}\equiv \text{O}}\text{A }\!\!’\!\!\text{ }$ (ảnh ảo, tại cực cận)
với: $\text{d }\!\!’\!\!\text{ }=-{{\text{O}}_{\text{k}}}{{\text{C}}_{\text{c}}}=-\text{O}{{\text{C}}_{\text{c}}}=-25\text{cm};\text{ f}=10\text{cm}\text{.}$
Suy ra: $\text{d}=\frac{\text{d }\!\!’\!\!\text{ f}}{\text{d }\!\!’\!\!\text{ }-\text{f}}=\frac{\left( -25 \right).10}{-25-10}=7,14\text{cm}.$
Độ bội giác của kính và độ phóng đại của ảnh:
${{\text{G}}_{\text{c}}}=\left| \text{k} \right|=\left| -\frac{\text{d }\!\!’\!\!\text{ }}{\text{d}} \right|=\left| -\frac{-25}{7,14} \right|=3,5.$
|
Bài tập 2: Một người cận thị có điểm Cc, Cv cách mắt lần lượt 10 cm và 50 cm. Người này dùng kính lúp có độ tụ +10 dp để quan sát một vật nhỏ. Mắt đặt sát kính. a) Vật phải đặt trong khoảng nào trước kính? b) Tính độ bội giác của kính và độ phóng đại của ảnh trong các trường hợp: +) Ngắm chừng ở Cv. +) Ngắm chừng ở Cc. |
Lời giải chi tiết:
a) Khoảng đặt vật trước kính là MN sao cho ảnh của M, N qua kính lúp là các ảnh ảo lần lượt tại Cc, Cv.
Sơ đồ tạo ảnh: $\text{M}\xrightarrow{{{\text{O}}_{\text{k}}}\equiv \text{O}}{{\text{A}}_{\text{1}}}$ (ảnh ảo, tại Cc)
$\text{N}\xrightarrow{{{\text{O}}_{\text{k}}}\equiv \text{O}}{{\text{A}}_{\text{2}}}$ (ảnh ảo, tại Cv)
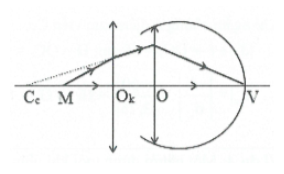Với $\text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }}=-{{\text{O}}_{\text{k}}}{{\text{C}}_{\text{c}}}=-\text{O}{{\text{C}}_{\text{c}}}=-10\text{cm};$$\text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }}=-{{\text{O}}_{\text{k}}}{{\text{C}}_{\text{v}}}=-\text{O}{{\text{C}}_{\text{v}}}=-50\text{cm}$
$\text{f}=\frac{1}{\text{D}}=\frac{1}{+10}=0,1\text{m}=10\operatorname{cm}$
$\Rightarrow {{\text{d}}_{\text{c}}}=\frac{\text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }}\text{f}}{\text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }}-\text{f}}=\frac{\left( -10 \right).10}{-10-10}=5\operatorname{cm}$
${{\text{d}}_{\text{v}}}=\frac{\text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }}\text{f}}{\text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }}-\text{f}}=\frac{\left( -50 \right).10}{-50-10}=\frac{50}{6}=8,3\operatorname{cm}.$
Vậy phải đặt vật trước kính cách mắt từ 5cm đến 8,3cm.
b) Khi ngắm chừng ở điểm cực viễn Cv:
+) Độ phóng đại của ảnh: ${{\text{k}}_{\text{v}}}=-\frac{\text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }}}{{{\text{d}}_{\text{v}}}}=-\frac{-50}{50/6}=6$
+) Độ bội giác của kính: ${{\text{G}}_{\text{v}}}=\left| {{\text{k}}_{\text{v}}} \right|.\frac{\text{}}{\left| \text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }} \right|+\ell }$
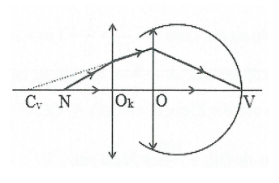với: $\left| \text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }} \right|+\ell =\text{O}{{\text{C}}_{\text{v}}}=50\text{cm};$$\text{}=10\text{cm}\Rightarrow {{\text{G}}_{\text{v}}}=6.\frac{10}{50}=1,2.$
Khi ngắm chừng ở điểm cực cận Cc:
+) Độ phóng đại của ảnh: ${{\text{k}}_{\text{c}}}=-\frac{\text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }}}{{{\text{d}}_{\text{c}}}}=-\frac{-10}{5}=2.$
+) Độ bội giác của kính: ${{\text{G}}_{\text{c}}}={{\text{k}}_{\text{c}}}.\frac{\text{}}{\left| \text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }} \right|+\ell }$
với: $\text{}=\left| \text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }} \right|+\ell \Rightarrow {{\text{G}}_{\text{c}}}={{\text{k}}_{\text{c}}}=2.$
|
Bài tập 3: Kính lúp có f = 4 cm. Mắt người quan sát có giới hạn nhìn rõ từ 11 cm đến 65 cm. Mắt đặt cách kính 5 cm. a) Xác định phạm vi ngắm chừng. |
|
b) Tính độ bội giác của kính ứng với trường hợp mắt không điều tiết. |
Lời giải chi tiết:
a) Phạm vi ngắm chừng của mắt khi quan sát qua kính lúp là khoảng phải đặt vật trước kính MN sao cho ảnh của M, N qua kính lúp là các ảnh ảo lần lượt tại Cc, Cv.
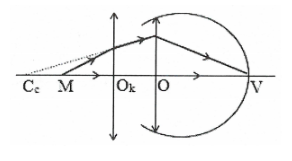Sơ đồ tạo ảnh: $\text{M}\xrightarrow{{{\text{O}}_{\text{k}}}}\text{M }\!\!’\!\!\text{ }$ (ảnh ảo, tại Cc)
$\text{N}\xrightarrow{{{\text{O}}_{\text{k}}}}\text{N }\!\!’\!\!\text{ }$ (ảnh ảo, tại Cv)
Ta có: $\text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }}=-{{\text{O}}_{\text{k}}}{{\text{C}}_{\text{c}}}=-\left( \text{O}{{\text{C}}_{\text{c}}}-\ell \right)=-\left( 11-5 \right)=-6\operatorname{cm}.$
$\text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }}=-{{\text{O}}_{\text{k}}}{{\text{C}}_{\text{v}}}=-\left( \text{O}{{\text{C}}_{\text{v}}}-\ell \right)=-\left( 65-5 \right)=-60\text{cm}.$
f = 4cm.
Suy ra: ${{\text{d}}_{\text{c}}}=\frac{\text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }}\text{f}}{\text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }}-\text{f}}=\frac{\left( -6 \right).4}{-6-4}=2,4\text{cm}$
${{\text{d}}_{\text{v}}}=\frac{\text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }}\text{f}}{\text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }}-\text{f}}=\frac{\left( -60 \right).4}{-60-4}=3,75\text{cm}$
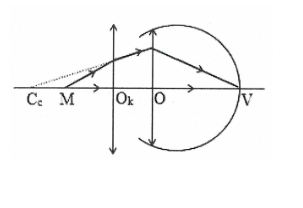Vậy phạm vi ngắm chừng cách mắt từ 2,4 cm đến 3,75 cm.
b) Mắt không điều tiết thì phải quan sát ảnh ở điểm cực viễn Cv.
Ta có: ${{\text{G}}_{\text{v}}}=\left| {{\text{k}}_{\text{v}}} \right|.\frac{\text{}}{\left| \text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }} \right|+\ell }$
Khi ngắm chừng ở điểm cực viễn Cv:
$\left| \text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }} \right|+\ell =\text{O}{{\text{C}}_{\text{v}}}=65\text{cm};\text{ }=\text{O}{{\text{C}}_{\text{c}}}=11\text{cm}:$
$\left| {{\text{k}}_{\text{v}}} \right|=\left| \frac{-\text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }}}{{{\text{d}}_{\text{v}}}} \right|=\left| \frac{-60}{3,75} \right|=16\Rightarrow {{\text{G}}_{\text{v}}}=16.\frac{11}{65}=2,7$.
|
Bài tập 4: Một người đứng tuổi khi nhìn những vật ở xa thì không phải đeo kính nhưng khi đeo kính (sát mắt) có tụ số 1dp thì đọc được trang sách đặt gần nhất là 25 cm. a) Xác định vị trí của các điểm cực viễn và cực cận của mắt người này. b) Xác định độ biến thiên của độ tụ mắt người này từ trạng thái không điều tiết đến điều tiết tối đa. c) Người này bỏ kính ra và dùng một kính lúp trên vành có ghi X8 để quan sát một vật nhỏ (lấy Đ = 25 cm). Mắt cách kính 30 cm. Phải đặt vật trong khoảng nào trước kính? Xác định |
|
phạm vi biến thiên của độ bội giác ảnh. |
Lời giải chi tiết:
a) Điểm cực viễn Cv: Mắt nhìn rõ vật ở xa không đeo kính nên Cv ở xa vô cùng.
Tiêu cự của kính: $\text{f}=\frac{1}{\text{D}}=\frac{1}{1}=1\text{m}=100\text{cm}.$
Sơ đồ tạo ảnh: $\text{A}\xrightarrow{{{\text{O}}_{\text{k}}}}\text{A }\!\!’\!\!\text{ }$ (ảnh ảo, tại Cc)
Ta có: $\text{d}=25\text{cm};\text{d }\!\!’\!\!\text{ }=-{{\text{O}}_{\text{k}}}{{\text{C}}_{\text{c}}}=-\text{O}{{\text{C}}_{\text{c}}}=\frac{\text{df}}{\text{d}-\text{f}}=\frac{25.100}{25-100}=-\frac{100}{3}\text{cm}$
Suy ra: $\text{O}{{\text{C}}_{\text{c}}}=\frac{100}{3}=33,33\text{cm}\text{.}$
b) Độ tụ cực đại của mắt (khi quan sát tại Cc): ${{\text{D}}_{\text{max}}}={{\text{D}}_{\text{c}}}=\frac{1}{{{\text{f}}_{\text{c}}}}=\frac{1}{\text{O}{{\text{C}}_{\text{c}}}}+\frac{1}{\text{OV}}$
Độ tụ cực tiểu của mắt (khi quan sát tại Cv 
): ${{\text{D}}_{\text{min}}}={{\text{D}}_{\text{v}}}=\frac{\text{1}}{{{\text{f}}_{\text{v}}}}=\frac{\text{1}}{\text{O}{{\text{C}}_{\text{v}}}}+\frac{\text{1}}{\text{OV}}=\frac{1}{\infty }+\frac{\text{1}}{\text{OV}}=\frac{\text{1}}{\text{OV}}$
Độ biến thiên độ tụ của mắt: $\Delta \text{D}={{\text{D}}_{\text{max}}}-{{\text{D}}_{\text{min}}}=\frac{1}{{{\text{d}}_{\text{c}}}}=\frac{1}{100/3}=3\text{dp}\text{.}$
c) Tiêu cự của kính: $\text{f}=\frac{25}{8}=3,125\text{cm}\text{.}$Sơ đồ tạo ảnh: $\text{A}\xrightarrow{{{\text{O}}_{\text{k}}}}\text{A }\!\!’\!\!\text{ }$ (ảnh ảo tại Cc hoặc Cv)
+) Khi quan sát ở Cc: $\text{d }\!\!’\!\!\text{ }=\text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }}=-{{\text{O}}_{\text{k}}}{{\text{C}}_{\text{c}}}=-\left( \text{O}{{\text{C}}_{\text{c}}}-\ell \right)=-\left( \frac{100}{3}-30 \right)=\frac{10}{3}=-3,33\text{cm}.$
$\Rightarrow \text{d}={{\text{d}}_{\text{c}}}={{\text{O}}_{\text{k}}}\text{A}=\frac{\text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }}\text{f}}{\text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }}-\text{f}}=\frac{\left( -10/3 \right).3,125}{-10/3-3,125}=1,61\text{cm}\text{.}$
+) Khi quan sát ở Cv: $\text{d }\!\!’\!\!\text{ }=\text{d}_{\text{v}}^{\text{ }\!\!’\!\!\text{ }}=-{{\text{O}}_{\text{k}}}{{\text{C}}_{\text{v}}}=-\left( \text{O}{{\text{C}}_{\text{v}}}-\ell \right)=-\infty $
$\Rightarrow \text{d}={{\text{d}}_{\text{v}}}=\text{f}=3,125\text{cm}\approx 3,13\text{cm}.$
Vậy khoảng đặt vật trước kính là $1,61\text{cm}\le \text{d}\le 3,13\text{cm}\text{.}$
+) Khi ngắm chừng ở Cc: ${{\text{G}}_{\text{c}}}=\left| {{\text{k}}_{\text{c}}} \right|=\left| -\frac{\text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }}}{{{\text{d}}_{\text{c}}}} \right|=\left| -\frac{3,33}{1,61} \right|=2,07.$
+) Khi ngắm chừng ở Cv : ${{\text{G}}_{\text{v}}}=\text{G}\infty =\frac{\text{}}{\text{f}}=\frac{\text{O}{{\text{C}}_{\text{c}}}}{\text{f}}=\frac{100/3}{3,125}=10,67.$
Vậy phạm vi biến thiên của độ bội giác của ảnh là $2,07\le \text{G}\le 10,67.$
