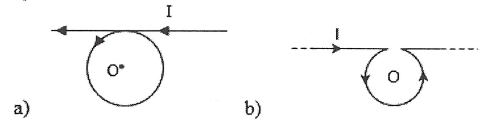VẤN ĐỀ 1: TỪ TRƯỜNG.
LÝ THUYẾT TRỌNG TÂM
1. Từ trường là không gian xung quanh thanh nam châm hay xung quanh dòng điện,… Gây ra lực từ tác dụng lên một nam châm hay một dòng điện khác đặt trong nó.
Quy ước hướng của từ trường là hướng Nam – Bắc của kim nam châm cân bằng tại điểm đó.
|
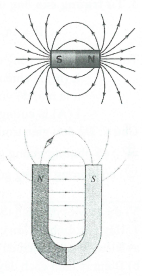
2. Đường sức từ là đường được vẽ sao cho hướng của tiếp tuyến tại bất kì điểm nào trên đường cũng trùng với hướng của vectơ cảm ứng từ tại điểm đó. – Tính chất: +) Tại mỗi điểm trong từ trường chỉ vẽ được một đường sức từ. +) Các đường sức từ là các đường cong khép kín, vô hạn ở hai đầu và không cắt nhau. +) Chiều của đường sức từ tuân theo quy tắc xác định (quy tắc nắm tay phải, quy tắc vặn đinh ốc,…). Trong trường hợp nam châm, các đường sức từ đi ra từ cực Bắc, đi vào ở cực Nam của nam châm. +) Nơi nào cảm ứng từ lớn hơn thì các đường sức từ ở đó vẽ mau hơn (dày hơn), nơi nào cảm ứng từ nhỏ hơn thì các đường sức từ ở đó vẽ thưa hơn. |
|
|
3. Từ trường đều là từ trường mà đặc tính của nó giống nhau tại mọi điểm; các đường sức từ là những đường thẳng song song, cùng chiều và cách đều nhau.
4. Từ trường của trái đất gây bởi một thanh nam châm khổng lồ nằm trong lòng trái đất, hay đầu nam châm này hướng về hai địa cực từ của trái đất. Góc tạo bởi trục quay của Trái đất và nam châm khổng lồ đó bằng 11°. |
|
CÁC DẠNG BÀI TẬP
DẠNG 1: CẢM ỨNG TỪ.
1.1: Từ trường của các dòng điện đặc biệt.
LÝ THUYẾT CHUNG
|
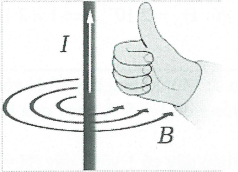
1. Từ trường của dòng điện thẳng dài vô hạn. ${{B}_{M}}={{2.10}^{-7}}.\frac{I}{{{r}_{M}}}$ Trong đó: ${{B}_{M}}\left( T \right)$ là từ trường tại điểm M ${{r}_{M}}\left( m \right)$ là khoảng cách từ sợi dây đến điểm M I (A) là cường độ dòng điện chạy qua sợi dây. |
|
Cách vẽ $\overrightarrow{B}$ tuân theo qui tắc nắm tay phải: “Để bàn tay phải sao cho ngón cái nằm dọc theo dây dẫn và chỉ theo chiều dòng điện, khi đó các ngón tay kia khum lại cho ta chiều của các đường sức từ”.
|
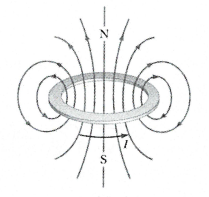
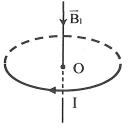
2. Từ trường của dòng điện tròn. ${{B}_{O}}=2\pi {{.10}^{-7}}\frac{I}{R}$ Trong đó: ${{B}_{O}}\left( T \right)$ là từ trường tại tâm O của vòng dây I (A) là cường độ dòng điện chạy trong vòng dây R (m) là bán kính của vòng dây. Cách vẽ $\overrightarrow{B}$ phải tuân theo qui tắc nắm tay phải: “Để bàn tay phải sao cho ngón cái nằm dọc theo dây dẫn và chỉ theo chiều dòng điện, khi đó các ngón kia khum lại cho ta chiều của cảm ứng từ.” |
|
|
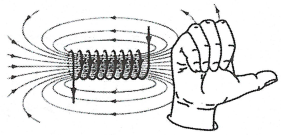
3. Từ trường của ống dây. $B=4\pi {{.10}^{-7}}\frac{NI}{L}=4\pi {{.10}^{-7}}nI$ Trong đó: N là số vòng dây L (m) là chiều dài ống dây n là mật độ vòng dây I (A) là cường độ dòng điện qua ống dây. |
|
Chú ý: Để đơn giản trong quá trình làm bài tập và biểu diễn vécto người ta quy ước như sau:
⊕ : Có phương vuông góc với mặt phẳng biểu diễn, chiều đi vào.
⊙ : Có phương vuông góc với mặt phẳng biểu diễn, chiều đi ra.
VÍ DỤ MINH HỌA
|
Bài tập 1: Một dây dẫn thẳng dài vô hạn, dòng điện chạy trong dây có cường độ I = 10 A. 1. Hãy xác định độ lớn cảm ứng từ do dòng điện trên gây ra tại: a) Điểm M nằm cách dây dẫn 5cm. b) Điểm N nằm cách dây dẫn 8cm. 2. Ở điểm D có cảm ứng từ là ${{2.10}^{-5}}T$, điểm D nằm cách dây dẫn 1 đoạn bằng bao nhiêu ? |
Lời giải chi tiết:
1. a) Cảm ứng từ tại M: ${{B}_{M}}={{2.10}^{-7}}.\frac{I}{r}={{2.10}^{-7}}.\frac{10}{0,05}={{4.10}^{-5}}T$ .
1. b) Cảm ứng từ tại N: ${{B}_{N}}={{2.10}^{-7}}.\frac{I}{r}={{2.10}^{-7}}.\frac{10}{0,08}=2,{{5.10}^{-5}}T$ .
2. Ta có : ${{B}_{D}}={{2.10}^{-7}}.\frac{I}{r}\Rightarrow r={{2.10}^{-7}}.\frac{I}{B}=0,1m=10cm$ .
|
Bài tập 2: Một khung dây có N vòng dây như nhau dạng hình tròn có bán kính 5 cm. Cho dòng điện có cường độ I = 5 A chạy qua khung dây. Hãy xác định vecto cảm ứng từ tại tâm của khung dây nếu: a) Khung dây có 1 vòng dây (N = 1). b) Khung dây có 10 vòng dây (N = 10). |
Lời giải chi tiết:
a) Cảm ứng tại tâm O có phương và chiều theo quy tắc nắm bàn tay phải. Phương $\overrightarrow{{{B}_{1}}}$ vuông góc với mặt
|
phẳng khung dây và chiều hướng xuống (nếu dòng điện cùng chiều kim đồng hồ) (như hình vẽ). Độ lớn: $B=2\pi {{.10}^{-7}}\frac{I}{r}=2\pi {{.10}^{-7}}\frac{5}{0,05}=2\pi {{.10}^{-5}}T$ |
|
b) Cảm ứng từ gây ra tại tâm của khung dây gồm nhiều vòng dây có điểm đặt, phương và chiều giống cảm ứng từ của 1 vòng dây, chỉ khác nhau về độ lớn.
Độ lớn cảm ứng từ của khung dây có 10 vòng dây:
${{B}_{10}}=2\pi {{.10}^{-7}}\frac{N.I}{r}=2\pi {{.10}^{-7}}\frac{10.5}{0,05}=2\pi {{.10}^{-4}}T$
Hay ${{B}_{10}}=N{{B}_{1}}=10{{B}_{1}}=2\pi {{.10}^{-4}}T$
|
Bài tập 4: Dùng một dây đồng có đường kính d = 0,8 mm có một lớp sơn cách điện mỏng, quấn quanh một hình trụ có đường kính D = 2 cm, chiều dài 40 cm để làm một ống dây, các vòng dây quấn sát nhau. Muốn từ trường có cảm ứng từ bên trong ống dây bằng $2\pi {{.10}^{-3}}T$ thì phải đặt vào ống dây một hiệu điện thế là bao nhiêu. Biết điện trở suất của đồng bằng $1,{{76.10}^{-8}}\Omega m$ . |
Lời giải chi tiết:
Gọi N là số vòng dây phải quấn trên ống dây. Đường kính của dây quấn chính là bề dày một vòng quấn, để quấn hết chiều dài ống dây $\ell $ thì phải cần N vòng quấn nên:
$N.d=\ell \Rightarrow \frac{N}{\ell }=\frac{1}{d}\Rightarrow N=\frac{\ell }{d}=500$ vòng
Ta có: $B=4\pi {{.10}^{-7}}.\frac{N}{\ell }.I\Rightarrow I=\frac{B}{4\pi {{.10}^{-7}}.n}=4\text{A}$
Điện trở của dây quấn: $\text{R=}\rho \frac{L}{S}=\rho \frac{L}{{r{{\text{d}}^{2}}}/{4}\;}\left( * \right)$
Chiều dài mỗi vòng quấn là chiều dài chu vi vòng tròn: $C=2\pi \text{r}=\pi \text{D}$
Chiều dài dây quấn: $L=N.C=N.\pi D$
Thay vào (*) ta được: $R=\rho \frac{N.\pi \text{D}}{{\pi {{\text{d}}^{2}}}/{4}\;}=\rho \frac{4N.D}{{{d}^{2}}}=1,1\Omega $
Hiệu điện thế ở hai đầu ống dây: $U=IR=4,4$ V.
|
Bài tập 5: Một ống dây có chiều dài 20 cm, gồm 500 vòng dây, cho cường độ dòng điện I = 5A chạy trong ống dây. a) Hãy xác định độ lớn cảm ứng từ bên trong ống dây? b) Nếu đồng thời tăng chiều dài ống dây, số vòng dây và cường độ dòng điện lên 2 lần thì cảm ứng từ bên trong ống dây lúc này có độ lớn là bao nhiêu? c) Cần phải dùng dòng điện có cường độ bao nhiêu để cảm ứng từ bên trong ống dây giảm đi một nửa so với câu a. |
Lời giải chi tiết:
a) Độ lớn cảm ứng từ bên trong ống dây: $B=4\pi {{.10}^{-7}}\frac{NI}{\ell }=0,0157T$
b) Ta có $B=4\pi {{.10}^{-7}}\frac{NI}{\ell }$ nên nếu đồng thời tăng chiều dài ống dây, số vòng dây và cường độ dòng điện lên 2 lần thì cảm ứng từ bên trong ống dây lúc này tăng lên 2 lần.
Do đó ta có: ${B}’=2B=0,0314T$
c) Ta có $B=4\pi {{.10}^{-7}}\frac{NI}{\ell }$ nên để B giảm 2 lần thì I phải giảm 2 lần. Do đó: ${I}’=\frac{I}{2}=2,5A$ .
|
Bài tập 6: Một dây đồng có đường kính d = 0,8 mm có phủ sơn cách điện mỏng quấn quanh một hình trụ đường kính D = 5 cm để tạo thành một ống dây. Khi nối ống dây với nguồn $\xi =4V$ , $r=0,5\Omega $ thì cảm ứng từ trong lòng ống dây là $B=5\pi {{.10}^{-4}}T$ . Tìm cường độ dòng điện trong ống và chiều dài ống dây, biết điện trở suất của dây quấn là $\rho =1,{{76.10}^{-8}}\Omega .m$ . |
Lời giải chi tiết:
Mật độ vòng dây: $n=\frac{1}{d}=\frac{1}{0,{{8.10}^{-3}}}=1250$ vòng/m
Cảm ứng từ: $B=4\pi {{.10}^{-7}}.n.I\Rightarrow I=\frac{B}{4\pi {{.10}^{-7}}.n}=1A$
Lại có: $I=\frac{\xi }{R+r}\Rightarrow R=\frac{\xi }{1}-r=3,5\Omega $
Chiều dài dây dẫn (dây quấn): $\ell =\frac{R.S}{\rho }=\frac{R.\left( \pi \frac{{{d}^{2}}}{4} \right)}{\rho }=\frac{3,5.\left( \pi \frac{{{\left( 0,{{8.10}^{-3}} \right)}^{2}}}{4} \right)}{1,{{76.10}^{-8}}}=99,96$ m
Số vòng dây: $N=\frac{\ell }{\pi D}=\frac{99,96}{\pi .0,05}=636,36$ vòng
Chiều dài ống dây: $L=\frac{N}{n}=0,51$ m.
1.2: Cảm ứng từ tổng hợp. Nguyên lí chồng chất từ trường.
LÝ THUYẾT CHUNG
a) Cảm ứng từ tổng hợp tại một điểm.
Vecto cảm ứng từ $\overrightarrow{B}$ tại một điểm do nhiều dòng điện gây ra: $\overrightarrow{B}=\overrightarrow{{{B}_{1}}}+\overrightarrow{{{B}_{2}}}+…+\overrightarrow{{{B}_{n}}}$
+) Trường hợp tổng quát $\left( \overrightarrow{{{B}_{1}}},\overrightarrow{{{B}_{2}}} \right)=\alpha \Rightarrow B=\sqrt{B_{1}^{2}+B_{2}^{2}+2{{B}_{1}}{{B}_{2}}\cos \alpha }$
+) Trường hợp đặc biệt thứ nhất $\overrightarrow{{{B}_{1}}}\uparrow \uparrow \overrightarrow{{{B}_{2}}}\Rightarrow \alpha ={{0}^{\circ }}\Rightarrow B={{B}_{1}}+{{B}_{2}}$
+) Trường hợp đặc biệt thứ hai $\overrightarrow{{{B}_{1}}}\uparrow \downarrow \overrightarrow{{{B}_{2}}}\Rightarrow \alpha ={{180}^{\circ }}\Rightarrow B=\left| {{B}_{1}}-{{B}_{2}} \right|$
+) Trường hợp đặc biệt thứ ba $\overrightarrow{{{B}_{1}}}\bot \overrightarrow{{{B}_{2}} {} }\Rightarrow \alpha ={{90}^{\circ }}\Rightarrow B=\sqrt{B_{1}^{2}+B_{2}^{2}}$
+) Nếu ${{B}_{1}}={{B}_{2}}\Rightarrow B=2{{B}_{1}}\cos \frac{\alpha }{2}$ .
b) Cảm ứng từ tổng hợp tại một điểm bằng không.
Bước 1: Tính ${{B}_{1}},{{B}_{2}},…$do ${{I}_{1}},{{I}_{2}}$ gây ra tại M
Bước 2: Cảm ứng từ tổng hợp tại M bằng 0: $\overrightarrow{{{B}_{M}}}=\overrightarrow{{{B}_{1}}}+\overrightarrow{{{B}_{2}}}=\overrightarrow{0}\Rightarrow \overrightarrow{{{B}_{1}} {} }=-\overrightarrow{{{B}_{2}}}$ , tức là:
+) $\overrightarrow{{{B}_{1}}}$ và $\overrightarrow{{{B}_{2}}}$ ngược chiều nhau.
+) Độ lớn bằng nhau: ${{B}_{1}}={{B}_{2}}\Rightarrow $ phương trình chứa ${{r}_{1}},{{r}_{2}}$ . Kết hợp với đề bài tìm ra ${{r}_{1}},{{r}_{2}}$ là vị trí để cảm ứng từ tại đó bằng 0.
VÍ DỤ MINH HỌA
|
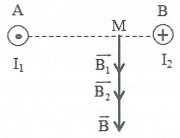
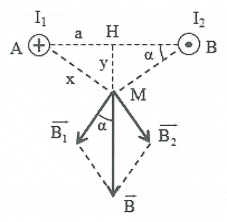
Bài tập 7: Hai dây dẫn thẳng, rất dài, đặt song song, cách nhau 20 cm trong không khí, có hai dòng điện ngược chiều, có cường độ ${{I}_{1}}=12\text{A}$; ${{I}_{2}}=15\text{A}$ chạy qua. Xác định cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm M cách dây dẫn mang dòng ${{I}_{1}}$ 15 cm và cách dây dẫn mang dòng ${{I}_{2}}$ 5 cm. |
Lời giải chi tiết:
Giả sử 2 dây dẫn ngược chiều được đặt vuông góc với mặt phẳng hình vẽ
|
${{B}_{1}}={{2.10}^{-7}}\frac{{{I}_{1}}}{AM}=1,{{6.10}^{-5}}T$ ;${{B}_{2}}={{2.10}^{-7}}\frac{{{I}_{2}}}{BM}={{6.10}^{-5}}T$ . Cảm ứng từ tổng hợp tại M là $\overrightarrow{B}=\overrightarrow{{{B}_{1}}}+\overrightarrow{{{B}_{2}}}$ Vì $\overrightarrow{{{B}_{1}}}$ và $\overrightarrow{{{B}_{2}}}$ cùng phương, cùng chiều nên $\overrightarrow{B}$ cùng phương, cùng chiều với $\overrightarrow{{{B}_{1}}}$ và $\overrightarrow{{{B}_{2}}}$ và có độ lớn $B={{B}_{1}}+{{B}_{2}}=7,{{6.10}^{-5}}T$ . |
|
|
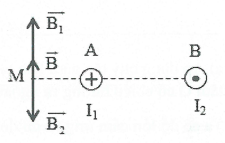
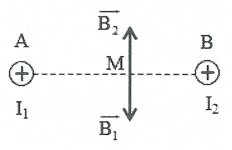
Bài tập 8: Hai dây dẫn thẳng, rất dài, đặt song song, cách nhau 10 cm trong không khí, có hai dòng điện ngược chiều, có cường độ ${{I}_{1}}=6\text{A};{{I}_{2}}=12\text{A}$ chạy qua. Xác định cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm M cách dây dẫn mang dòng ${{I}_{1}}$ 5 cm và cách dây dẫn mang dòng ${{I}_{2}}$ 15 cm. |
Lời giải chi tiết:
Giả sử hai dây dẫn được đặt vuông góc với mặt phẳng hình vẽ.
|
${{B}_{1}}={{2.10}^{-7}}\frac{{{I}_{1}}}{AM}=2,{{4.10}^{-5}}T$ ;${{B}_{2}}={{2.10}^{-7}}\frac{{{I}_{2}}}{BM}=1,{{6.10}^{-5}}T$ . Cảm ứng từ tổng hợp tại M là: $\overrightarrow{B}=\overrightarrow{{{B}_{1}}}+\overrightarrow{{{B}_{2}}}$ . Vì $\overrightarrow{{{B}_{1}}}$ và $\overrightarrow{{{B}_{2}}}$ cùng phương, ngược chiều và ${{B}_{1}}>{{B}_{2}}$ nên $\overrightarrow{B}$ cùng phương, chiều với $\overrightarrow{{{B}_{1}}}$ và có độ lớn: $B={{B}_{1}}-{{B}_{2}}=0,{{8.10}^{-5}}T$ |
|
|
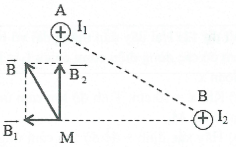
Bài tập 9: Hai dây dẫn thẳng, rất dài, đặt song song, cách nhau 10 cm trong không khí, có hai dòng điện cùng chiều, có cường độ ${{I}_{1}}=9\text{A}$ ; ${{I}_{2}}=16\text{A}$ chạy qua. Xác định cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm M cách dây dẫn mang dòng ${{I}_{1}}$ 6 cm và cách dây dẫn mang dòng ${{I}_{2}}$ 8 cm. |
Lời giải chi tiết:
Giả sử hay dây dẫn được đặt vuông góc với mặt phẳng hình vẽ.
|
${{B}_{1}}={{2.10}^{-7}}\frac{{{I}_{1}}}{AM}={{3.10}^{-5}}T$ ${{B}_{2}}={{2.10}^{-7}}\frac{{{I}_{2}}}{BM}={{4.10}^{-5}}T$ . Cảm ứng từ tổng hợp tại M là: $\overrightarrow{B}=\overrightarrow{{{B}_{1}}}+\overrightarrow{{{B}_{2}}}$ Từ hình vẽ, suy ra độ lớn: $B=\sqrt{B_{1}^{2}+B_{2}^{2}}={{5.10}^{-5}}T$ . |
|
|
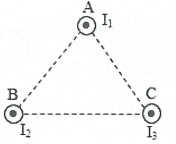
Bài tập 10: Ba dòng điện cùng cường độ 5 A chạy trong ba dây dẫn thẳng, song song, có chiều như hình vẽ. Biết tam giác ABC đều cạnh 10 cm, độ lớn cảm ứng từ tại tâm O của tam giác bằng bao nhiêu? |
|
Lời giải chi tiết:
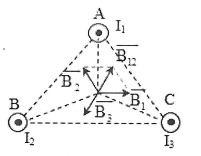
Áp dụng quy tắc nắm bàn tay phải xác định được chiều cảm ứng từ do 3 dòng điện gây ra tại tâm O của tam giác như hình vẽ. ($\overrightarrow{{{B}_{1}}},\overrightarrow{{{B}_{2}}},\overrightarrow{{{B}_{3}}}$ hợp với nhau góc 120°).
|
Độ lớn cảm ứng từ do dòng điện thẳng dài gây ra $B={{2.10}^{-7}}\frac{I}{r}$ $\Rightarrow {{B}_{1}}={{B}_{2}}={{B}_{3}}=\sqrt{3}{{.10}^{-5}}T$ Áp dụng quy tắc chồng chất từ trường $\overrightarrow{B}=\overrightarrow{{{B}_{1}}}+\overrightarrow{{{B}_{2}}}+\overrightarrow{{{B}_{3}}}=\overrightarrow{{{B}_{12}}}+\overrightarrow{{{B}_{3}}}$ ${{B}_{12}}=2{{B}_{1}}.\cos {{60}^{\circ }}={{B}_{1}}={{B}_{3}}\Rightarrow {{B}_{O}}=\left| {{B}_{12}}-{{B}_{3}} \right|=0$ . |
|
|
Bài tập 11: Một dây dẫn rất dài căng thẳng, ở giữa dây được uốn thành vòng tròn bán kính R = 1,5 cm, tại chỗ chéo nhau dây dẫn được cách điện. Dòng điện chạy trên dây có cường độ 3 A. Tính độ lớn cảm ứng từ tại tâm O của vòng tròn trong 2 trường hợp uốn dây như sau: |
Lời giải chi tiết:
a) Áp dụng quy tắc nắm bàn tay phải xác định được chiều cảm ứng từ do hai dòng điện gây ra tại tâm O có chiều hướng ra ngoài mặt phẳng hình vẽ nên ${{B}_{O}}={{B}_{1}}+{{B}_{2}}$
Ta có độ lớn cảm ứng từ do dòng điện thẳng gây ra tại O là ${{B}_{1}}={{2.10}^{-7}}\frac{I}{R}$
Độ lớn cảm ứng từ do dòng điện tròn gây ra tại tâm O là ${{B}_{2}}=2\pi {{.10}^{-7}}\frac{I}{R}$
$\Rightarrow $ Độ lớn cảm ứng từ do hai dòng điện gây ra tại O là ${{B}_{O}}={{2.10}^{-7}}\frac{I}{R}\left( \pi +1 \right)=16,{{6.10}^{-5}}T$ .
b) Chiều cảm ứng tại tâm O do dây dẫn thẳng gây ra có chiều hướng vào trong mặ phẳng hình vẽ, còn dây dẫn tròn gây ra tại tâm có chiều hướng ra ngoài mặt phẳng hình vẽ nên $B=\left| {{B}_{1}}-{{B}_{2}} \right|$
Ta có ${{B}_{1}}={{2.10}^{-7}}\frac{I}{r}$ ; ${{B}_{2}}=2\pi {{.10}^{-7}}\frac{I}{R}$ với $r=R=0,015m\Rightarrow B=\left| {{B}_{1}}-{{B}_{2}} \right|=8,{{6.10}^{-5}}T$ .
|
Bài tập 12: Hai dây dẫn thẳng dài vô hạn, đặt song song trong không khí cách nhau một đoạn d = 12 cm có các dòng điện cùng chiều ${{I}_{1}}={{I}_{2}}=I=10$ A chạy qua. Một điểm M cách đều hai dây dẫn một đoạn x. a) Khi x = 10 cm. Tính độ lớn cảm ứng từ tổng hợp do hai dòng điện chạy trong hai dây dẫn gây ra tại điểm M. b) Hãy xác định x để độ lớn cảm ứng từ tổng hợp do hai dòng điện gây ra đạt giá trị cực đại. Tính giá trị cực đại đó. |
Lời giải chi tiết:
a) Giả sử hai dây dẫn được đặt vuông góc với mặt phẳng hình vẽ.
|
Ta có: ${{B}_{1}}={{B}_{2}}={{2.10}^{-7}}\frac{I}{x}={{2.10}^{-5}}T$ . Cảm ứng từ tổng hợp tại M là: $\overrightarrow{B}=\overrightarrow{{{B}_{1}}}+\overrightarrow{{{B}_{2}}}$ $B={{B}_{1}}\cos \alpha +{{B}_{2}}\cos \alpha =2{{B}_{1}}\cos \alpha =2{{B}_{1}}\frac{\sqrt{{{x}^{2}}-{{\left( \frac{d}{2} \right)}^{2}}}}{x}=3,{{2.10}^{-5}}T$ . b) Theo câu a) ta có: ${{B}_{1}}={{B}_{2}}={{2.10}^{-7}}\frac{I}{x}$ ; |
|
$B=2{{B}_{1}}\cos \alpha ={{2.2.10}^{-7}}\frac{I}{x}\frac{\sqrt{{{x}^{2}}-{{\left( \frac{d}{2} \right)}^{2}}}}{x}={{4.10}^{-7}}I\sqrt{\frac{1}{{{x}^{2}}}-\frac{{{d}^{2}}}{4{{x}^{4}}}}$
B đạt cực đại khi $\frac{1}{{{x}^{2}}}-\frac{{{d}^{2}}}{4{{x}^{4}}}=\frac{4}{{{d}^{2}}}.\frac{{{d}^{2}}}{4{{x}^{2}}}\left( 1-\frac{{{d}^{2}}}{4{{x}^{2}}} \right)$ đạt cực đại
Theo bất đẳng thức Côsi thì $\frac{4}{{{d}^{2}}}.\frac{{{d}^{2}}}{4{{x}^{2}}}\left( 1-\frac{{{d}^{2}}}{4{{x}^{2}}} \right)$ đạt cực đại khi $\frac{{{d}^{2}}}{4{{x}^{2}}}=1-\frac{{{d}^{2}}}{4{{x}^{2}}}$
$\Rightarrow x=\frac{d}{\sqrt{2}}=8,5cm$ . Khi đó ${{B}_{\max }}=3,{{32.10}^{-5}}T$ .
|
Bài tập 13: Hai dây dẫn thằng dài vô hạn, đặt song song trong không khí cách nhau một đoạn d = 2a có các dòng điện ngược chiều cùng cường độ ${{I}_{1}}={{I}_{2}}=I$ chạy qua. a) Xác định cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm M cách đều hai dây dẫn một đoạn x. b) Hãy xác định x để độ lớn cảm ứng từ tổng hợp do hai dòng điện gây ra đạt giá trị cực đại. Tính giá trị cực đại đó. |
Lời giải chi tiết:
a) Giả sử hai dây dẫn được đặt vuông góc với mặt phẳng hình vẽ.
|
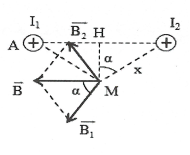
Ta có: ${{B}_{1}}={{B}_{2}}={{2.10}^{-7}}.\frac{I}{x}$ $\overrightarrow{{{B}_{M}}}=\overrightarrow{{{B}_{1}}}+\overrightarrow{{{B}_{2}}}$ có phương chiều như hình vẽ và có độ lớn: ${{B}_{M}}={{B}_{1}}\cos \alpha +{{B}_{2}}\cos \alpha =2{{B}_{1}}\cos \alpha $ $={{2.2.10}^{-7}}.\frac{I}{x}.\frac{a}{x}={{4.10}^{-7}}I\frac{a}{{{x}^{2}}}$ b) Đặt MH = y; ta có ${{x}^{2}}={{a}^{2}}+{{y}^{2}}\Rightarrow B={{4.10}^{-7}}I\frac{a}{{{a}^{2}}+{{y}^{2}}}$ B đạt cực đại khi $y=0\Rightarrow x=a$ ; khi đó ${{B}_{\max }}={{4.10}^{-7}}\frac{I}{a}$ . |
|
|
Bài tập 14: Hai dây dẫn thẳng, rất dài, đặt song song, cách nhau 15 cm trong không khí, có hai dòng điện cùng chiều, có cường độ ${{I}_{1}}=10A$ , ${{I}_{2}}=5\text{A}$ chạy qua. Xác định điểm M mà tại đó cảm ứng từ tổng hợp do hai dòng điện này gây ra bằng 0. |
Lời giải chi tiết:
Giả sử hai dây dẫn được đặt vuông góc với mặt phẳng hình vẽ. Để cảm ứng từ tổng hợp tại M bằng 0 thì $\overrightarrow{B}=\overrightarrow{{{B}_{1}}}+\overrightarrow{{{B}_{2}}}=\overrightarrow{0}\Rightarrow \overrightarrow{{{B}_{1}}}=-\overrightarrow{{{B}_{2}}}$ tức là $\overrightarrow{{{B}_{1}}}$ và $\overrightarrow{{{B}_{2}}}$ phải cùng phương, ngược chiều và bằng nhau về độ lớn.
|
Để thỏa mãn các điều kiện đó thì M phải nằm trên đường thẳng nối A, B; nằm trong đoạn thẳng AB. Với ${{B}_{1}}={{B}_{2}}$ thì ${{2.10}^{-7}}\frac{{{I}_{1}}}{AM}={{2.10}^{-7}}\frac{{{I}_{2}}}{AB-AM}$ $\Rightarrow AM=\frac{AB.I}{{{I}_{1}}+{{I}_{2}}}=10cm;\Rightarrow MB=5cm$ . |
|
|
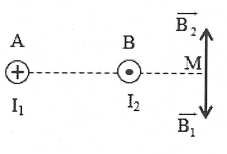
Bài tập 15: Hai dây dẫn thẳng, rất dài, đặt song song, cách nhau 10 cm trong không khí, có hai dòng điện ngược chiều, có cường độ ${{I}_{1}}=20A$, ${{I}_{2}}=10A$ chạy qua. Xác định điểm M mà tại đó cảm ứng từ tổng hợp do hai dòng điện này gây ra bằng 0. |
Lời giải chi tiết:
|
$\overrightarrow{B}=\overrightarrow{{{B}_{1}}}+\overrightarrow{{{B}_{2}}}=\overrightarrow{0}\Rightarrow \overrightarrow{{{B}_{1}}}=-\overrightarrow{{{B}_{2}}}$ Để thỏa mãn điều kiện đó thì M phải nằm trên đường thẳng nối A, B; nằm ngoài đoạn thẳng AB, gần dây dẫn mang dòng ${{I}_{2}}$ hơn (vì ${{I}_{1}}>{{I}_{2}}$ ). ${{B}_{1}}={{B}_{2}}\Leftrightarrow {{2.10}^{-7}}.\frac{{{I}_{1}}}{AM}={{2.10}^{-7}}.\frac{{{I}_{2}}}{AM-AB}$ $\Rightarrow AM=\frac{AB.{{I}_{1}}}{{{I}_{1}}-{{I}_{2}}}=20cm\Rightarrow BM=10cm$ . |
|
|
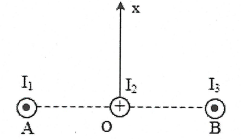
Bài tập 16: Ba dòng điện thẳng song song như hình vẽ. Biết ${{I}_{1}}={{I}_{3}}=I$ ; ${{I}_{2}}=\frac{1}{2}$ ; OA = OB = a. Những điểm trên trục Ox vuông góc với mặt phẳng chứa ba dây có B = 0 cách O một khoảng bằng bao nhiêu ? |
|
<