Tổng hợp lý thuyết ôn tập về mắt và các tật của mắt vật lý lớp 12

VẤN ĐỀ 2: MẮT

LÝ THUYẾT TRỌNG TÂM

1. Mắt thường.

– Định nghĩa: Về phương diện quang hình học, mắt giống như một máy ảnh, cho một ảnh thật nhỏ hơn vật trên võng mạc.

– Cấu tạo: 

+) Thủy tinh thể: Bộ phận chính là một thấu kính hội tụ có tiêu cự f thay đổi được.

+) Võng mạc: $\Leftrightarrow $màn ảnh, sát đáy mắt nơi tập trung các tế bào nhạy sáng ở đầu các dây thần kinh thị giác. Trên võng mạc có điểm vàng V rất nhạy sáng. Do d’ = OV = không đổi: để nhìn vật ở các khoảng cách khác nhau (d thay đổi) $\Rightarrow $f thay đổi (mắt phải điều tiết).

– Sự điều tiết của mắt – Điểm cực cận C_c – Điểm cực viễn C_v:

+) Sự điều tiết là sự thay đổi độ cong của thủy tinh thể (và do đó thay đổi độ tụ hay tiêu cự của nó) để làm cho ảnh của các vật cần quan sát hiện lên trên võng mạc.

+) Mắt thường khi không điều tiết có tiêu điểm nằm trên võng mạc (màng lưới).

+) Mắt bình thường có điểm cực cận C_c cách mắt cỡ 25cm (OC_c = Đ   25cm), điểm cực viễn ở vô cùng (OC_v =  )

+) Giới hạn nhìn rõ của mắt [C_c; C_v]

+) Công thức về thấu kính mắt: $\text{D}=\frac{1}{\text{f}}=\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}\xrightarrow{\text{d }\!\!’\!\!\text{ }=\text{OV}}\text{D}=\frac{1}{\text{f}}=\frac{1}{\text{d}}+\frac{1}{\text{OV}}$ 

Khi quan sát ở vô cực (không điều tiết) thì d = OC_v =  : $\text{D}=\frac{1}{\text{f}}=\frac{1}{\infty }+\frac{1}{\text{OV}}\Rightarrow \text{D}=\frac{1}{\text{f}}=\frac{1}{\text{OV}}$

Khi quan sát ở cực cận (điều tiết tối đa) thì d = OC_c = Đ: $\text{D}=\frac{1}{\text{f}}=\frac{1}{\text{O}{{\text{C}}_{\text{c}}}}+\frac{1}{\text{OV}}$

Khi chuyển từ trạng thái quan sát vật ở vị trí cách mắt d₁ sang trạng thái quan sát vật ở vị trí cách mắt d₂ thì độ biến thiên độ tụ của mắt là: $\Delta \text{D}=\frac{1}{{{\text{d}}_{2}}}-\frac{1}{{{\text{d}}_{1}}}$

Khi chuyển từ trạng thái không điều tiết sang trạng thái điều tiết tối đa thì: $\Delta \text{D}=\frac{1}{\text{O}{{\text{C}}_{\text{c}}}}-\frac{1}{\text{O}{{\text{C}}_{\text{v}}}}$

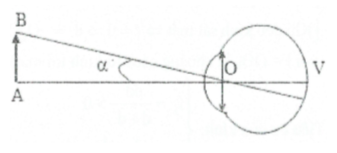
– Góc trông vật AB là góc   tạo bởi hai tia sáng 

xuất phát từ hai điểm A và B tới mắt.

Năng suất phân li của mắt  _min là góc trông nhỏ nhất 

giữa hai điểm mà mắt còn có thể phân biệt được 

hai điểm đó: $\tan \alpha =\frac{\text{AB}}{\text{OA}}=\frac{\text{AB}}{\ell }$

– Chú ý: Khi tính toán các công thức liên quan đến độ tụ D hay độ biến thiên độ tụ  D thì nhất thiết phải để đơn vị chiều dài ở dạng mét (m).

2. Mắt cận thị.

– Mắt cận thị là mắt khi không điều tiết có tiêu điểm nằm trước võng mạc. Do đó f_max < OV với OV là khoảng cách từ quang tâm thủy tinh thể tới võng mạc. Khoảng cực cận OC_c = Đ < 25cm, OC_v có giá trị hữu hạn.

– Cách sửa (có 2 cách, cách 1 có lợi nhất thường được sử dụng)

Cách 1: Đeo thấu kính phân kỳ để nhìn xa như người bình thường, tức là vật ở vô cực cho ảnh ảo qua kính nằm ở điểm cực viễn.

Sơ đồ tạo ảnh: 

Với  là khoảng cách từ kính tới mắt.

Cách 2: Đeo thấu kính phân kỳ để nhìn gần như người bình thường, tức là vật đặt cách mắt 25cm cho ảnh ảo qua kính nằm ở điểm cực cận.

Ta có:
 

 

với  là khoảng cách từ kính tới mắt.

– Chú ý: OC_c = Đ là khoảng thấy rõ ngắn nhất của mắt là khoảng cách từ điểm cực cận (C_c) đến mắt.

3. Mắt viễn thị.

– Là mắt khi không điều tiết có tiêu điểm nằm sau võng mạc (f_max > OV). Điểm cực cận ở xa hơn mắt bình thường (OC_c = Đ > 25cm)

– Cách sửa: Đeo thấu kính hội tụ để nhìn gần như người bình thường, tức là vật đặt cách mắt 25cm cho ảnh ảo qua kính nằm ở điểm cực cận.

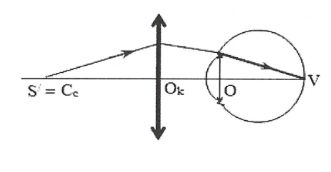Sơ đồ tạo ảnh: $\text{S}\xrightarrow{{{\text{O}}_{\text{k}}}}\text{S }\!\!’\!\!\text{ }\equiv {{\text{C}}_{\text{c}}}\xrightarrow{\text{O}}\text{S }\!\!’\!\!\text{  }\!\!’\!\!\text{ }\equiv \text{V}$

(với $\ell =\text{O}{{\text{O}}_{\text{k}}}$là khoảng cách từ kính tới mắt)

Tiêu cự của kính: $\left\{ \begin{array}{} {{\text{f}}_{\text{k}}}=\frac{\text{dd }\!\!’\!\!\text{ }}{\text{d}+\text{d }\!\!’\!\!\text{ }}>0 \\ {} {{\text{D}}_{\text{k}}}=\frac{1}{{{\text{f}}_{\text{k}}}}=\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }} \\ \end{array} \right.$

BÀI TẬP VỀ MẮT

Bài tập 1: Một người có mắt bình thường (không tật) nhìn thấy được các vật ở rất xa mà không phải điều tiết. Khoảng cực cận của người này là OCc = 25 cm. Độ tụ của mắt người này khi điều tiết tối đa tăng thêm bao nhiêu?

Lời giải chi tiết:

Theo bài ra: $\text{O}{{\text{C}}_{\text{c}}}=25\text{ cm, O}{{\text{C}}_{\text{v}}}=\infty .$

Ảnh thu được nằm trên võng mạc nên d’ = OV.

Áp dụng công thức về thấu kính mắt: $D=\frac{1}{f}=\frac{1}{d}+\frac{1}{d’}=\frac{1}{d}+\frac{1}{OV}$

Khi mắt nhìn vật ở điểm cực viễn (ngắm chừng ở cực viễn d = OC_v):

${{D}_{min}}=\frac{1}{{{f}_{max}}}=\frac{1}{OV}+\frac{1}{O{{C}_{v}}}=\frac{1}{OV}+\frac{1}{\infty }=\frac{1}{OV}$

Khi mắt nhìn vật ở điểm cực cận (ngắm chừng ở cực cận d = OC_c):

${{\operatorname{D}}_{max}}=\frac{1}{{{f}_{min}}}=\frac{1}{OV}+\frac{1}{O{{C}_{c}}}=\frac{1}{OV}+\frac{1}{0,25}$

Độ biến thiên độ tụ: $\Delta \text{D}={{\text{D}}_{\text{max}}}-{{\text{D}}_{\text{min}}}=\frac{1}{0,25}=4\text{dp}.$

Bài tập 2: Mắt một người bình thường về già, khi điều tiết tối đa thì tăng độ tụ thêm 1 dp. a) Xác định điểm cực cận và cực viễn của mắt. b) Tính độ tụ của thấu kính phải đeo (cách mắt 2 cm) để mắt nhìn thấy một vật cách 25 cm không điều tiết.

Lời giải chi tiết:

a) Điểm cực viễn của mắt bình thường ở vô cùng $\Rightarrow {{\operatorname{OC}}_{v}}=\infty $

Khi mắt nhìn vật ở điểm cực viễn: ${{D}_{min}}=\frac{1}{{{f}_{max}}}=\frac{1}{OV}+\frac{1}{O{{C}_{v}}}=\frac{1}{OV}+\frac{1}{\infty }=\frac{1}{OV}$

Khi mắt nhìn vật ở điểm cực cận: ${{\operatorname{D}}_{max}}=\frac{1}{{{f}_{min}}}=\frac{1}{OV}+\frac{1}{O{{C}_{c}}}$

Độ biến thiên độ tụ: $\Delta D={{D}_{max}}-{{D}_{min}}=\frac{1}{O{{C}_{c}}}=1dp\Rightarrow {{\operatorname{OC}}_{c}}=1\left( m \right)$

Vậy điểm cực cận của mắt người này cách mắt 100 cm.

b) Để mắt nhìn thấy vật mà không phải điều tiết thì qua kính ảnh phải hiện ở vô cùng $\Rightarrow \operatorname{d}’=\infty ,$muốn vậy thì vật phải đặt ở tiêu điểm vật của kính.

$\Rightarrow \operatorname{d}=f=O{{C}_{v}}-\ell =25-2=23\left( cm \right)=0,23\left( m \right)$

Vậy độ tụ của kính là: $\operatorname{D}=\frac{1}{f}=\frac{1}{0,23}=4,35dp.$

Bài tập 3: Một mắt bình thường có tiêu cự biến thiên fmin = 14 mm đến fmax. Biết khoảng cách từ thủy tinh thể đến võng mạc là 15mm. Tìm phạm vi nhìn rõ của mắt và độ biến thiên độ tụ của mắt khi chuyển từ trạng thái không điều tiết sang điều tiết tối đa.

Lời giải chi tiết:

Khoảng cách từ thủy tinh thể đến võng mạc: d’ = OV = 15 (mm) = 15.10^-3 (m)

Mắt bình thường, khi nhìn vật ở cực viễn C_v thì d = OC_v =   tiêu cự của thủy tinh thể lúc này cực đại f_max.

Ta có: ${{\operatorname{D}}_{min}}=\frac{1}{{{f}_{max}}}=\frac{1}{OV}+\frac{1}{O{{C}_{v}}}=\frac{1}{OV}+\frac{1}{\infty }=\frac{1}{15.1{{0}^{-3}}}=\frac{200}{3}dp$

Khi mắt nhìn vật ở cực cận C_c thì d = OC_c tiêu cự của thủy tinh thể lúc này cực tiểu ${{\operatorname{f}}_{min}}=14mm\Rightarrow {{\operatorname{D}}_{max}}=\frac{1}{{{f}_{min}}}=\frac{1}{14.1{{0}^{-3}}}=\frac{500}{7}dp$

Ta có: $\frac{1}{{{f}_{min}}}=\frac{1}{OV}+\frac{1}{O{{C}_{c}}}\Leftrightarrow \frac{1}{14}=\frac{1}{15}+\frac{1}{O{{C}_{c}}}\Rightarrow {{\operatorname{OC}}_{c}}=210\left( mm \right)=21\left( cm \right)$

Vậy phạm vi nhìn rõ của mắt người này từ 21 cm trở ra đến vô cùng

Độ biến thiên độ tụ của mắt khi chuyển từ trạng thái không điều tiết sang điều tiết tối đa:

$\Delta \operatorname{D}={{D}_{max}}-{{D}_{min}}=\frac{500}{7}-\frac{200}{3}=\frac{100}{21}\approx 4,76dp.$

Bài tập 4: Mắt có tiêu cự biến thiên từ 14 mm đến 14,8 mm, khoảng cách từ thủy tinh thể đến võng mạc là 15 mm.

a) Tìm giới hạn nhìn rõ của mắt và độ biến thiên độ tụ của mắt? b) Người này cần đeo kính loại gì, tiêu cự bao nhiêu để sửa tật? Khi đeo kính người này nhìn rõ khoảng gần nhất cách mắt bao nhiêu? (Biết kính đeo cách mắt 1 cm).

Lời giải chi tiết:

a) – Khoảng cách từ thủy tinh thể đến võng mạc OV = d’ = 15 mm

Khi mắt nhìn vật ở điểm cực viễn C_v: d = OC_v; tiêu cự của thủy tinh thể lúc này là cực đại: 

${{\operatorname{f}}_{max}}=14,8 mm\Rightarrow {{\operatorname{OC}}_{v}}=111 cm.$

Khi mắt nhìn vật ở điểm cực cận C_c: d = OC_c; tiêu cự của thủy tinh thể lúc này là cực tiểu: 

${{\text{f}}_{\min }}=14\text{ cm}\Rightarrow \text{O}{{\operatorname{C}}_{c}}=21 cm.$

Vậy, mắt người này nhìn được những vật đặt cách mắt từ 21 cm đến 111 (cm).

– Khoảng cách từ thủy tinh thể đến võng mạc d’ = OV không đổi; khoảng cách từ vật đến mắt là d.

Khi mắt nhìn vật ở điểm cực viễn: d = OC_v = 1,11 m; ${{\operatorname{D}}_{min}}=\frac{1}{{{f}_{max}}}=\frac{1}{OV}+\frac{1}{O{{C}_{v}}}\left( 1 \right)$

Khi mắt nhìn vật ở điểm cực cận C_c: d = OC_c = 0,21 m; ${{\operatorname{D}}_{max}}=\frac{1}{{{f}_{min}}}=\frac{1}{OV}+\frac{1}{O{{C}_{c}}}\left( 2 \right)$

$\Rightarrow \Delta \text{D}={{D}_{max}}-{{D}_{min}}=\frac{1}{O{{C}_{c}}}-\frac{1}{O{{C}_{v}}}=3,86\left( dp \right).$

b) Muốn sửa tật cận thị (hay muốn nhìn vật ở xa vô cực mà không cần điều tiết) cần đeo thấu kính phân kì có tiêu cự sao cho vật ở xa qua kính cho ảnh ảo ở điểm cực viễn của mắt. Mắt nhìn rõ mà không cần điều tiết.

Kính đeo cách mắt một khoảng $\ell =1\text{ cm:} {{f}_{k}}=-\left( {{\operatorname{OC}}_{v}}-\ell  \right)=-110\left( \text{cm} \right).$

Khi đeo kính này, vật gần nhất mắt nhìn rõ qua kính cho ảnh ảo ở điểm cực cận (C_c) của mắt:

$\text{d}_{\text{c}}^{\text{ }\!\!’\!\!\text{ }}\text{=}-\left( {{\operatorname{OC}}_{c}}-\ell  \right)=-20\left( cm \right).$

Áp dụng công thức thấu kính, suy ra: ${{\operatorname{d}}_{c}}=24,4\left( cm \right).$

Vậy khi đeo kính trên vật gần nhất mắt nhìn rõ cách kính 24,4 (cm) và cách mắt 25,4 (cm).

Bài tập 5: Mắt một người có điểm cực viễn Cv cách mắt 50 cm. a) Mắt người này bị tật gì? b) Muốn nhìn thấy vật ở vô cực không điều tiết, người đó phải đeo kính có độ tụ bao nhiêu? (Coi kính đeo sát mắt). c) Điểm Cc cách mắt 10 cm. Khi đeo kính trên (sát mắt) thì người đó nhìn thấy điểm gần nhất cách mắt bao nhiêu?

Lời giải chi tiết:

Mắt người bình thường ở điểm cực viễn C_v ở vô cùng và cực cận C_c cách mắt cỡ 25 cm (OC_c = 25cm). Mắt người viễn thị có điểm cực viễn C_v ở vô cùng và cực cận C_c xa hơn mắt thường (OC_c > 25cm).

Mắt người cận thị có điểm cực viễn C_v không nằm ở vô cùng mà cách mắt một khoảng cách hữu hạn nào đó và cực cận C_c gần hơn mắt thường (OC_c < 25cm).

Từ các đặc điểm của mắt như phân tích ở trên ta dễ dàng nhận ra tật của mắt người này như sau:

a) Điểm cực viễn C_v cách mắt 50 cm (giá trị hữu hạn) nên mắt người này bị cận thị.

b) Muốn mắt nhìn ở vô cực mà không phải điều tiết thì người này phải đeo kính có độ tụ D₁ sao cho vật đặt ở vô cực cho ảnh ảo ở điểm cực viễn của mắt.

Do đó ta có: $\operatorname{d}=\infty ;\text{d }\!\!’\!\!\text{ }=-\text{O}{{\text{C}}_{\text{v}}}<0$ (vì ảnh là ảnh ảo nên d’ < 0).

Độ tụ kính cần đeo: $\operatorname{D}=\frac{1}{f}=\frac{1}{d}+\frac{1}{d’}=\frac{1}{\infty }+\frac{1}{-O{{C}_{v}}}=-\frac{1}{0,5}\Rightarrow \operatorname{D}=-2\text{dp}$

c) Khi đeo kính trên mà nhìn vật cách mắt đoạn gần nhất là d, thì ảnh ảo sẽ hiện ở điểm cực cận của mắt (d’ = -10 cm).

Ta có: $\operatorname{D}=\frac{1}{f}=\frac{1}{d}+\frac{1}{d’}=\frac{1}{d}+\frac{1}{-{{\operatorname{OC}}_{c}}}\Leftrightarrow -2=\frac{1}{d}+\frac{1}{-0,1}\Rightarrow \operatorname{d}=0,125\left( m \right)=12,5\left( cm \right)$

Vậy khi đeo kính trên (kính đeo sát mắt) thì người đó nhìn thấy điểm gần nhất cách mắt 12,5 cm.

Bài tập 6: Một người đeo sát mắt một kính có độ dụ D = -1,25 dp thì nhìn rõ những vật nằm cách mắt trong khoảng từ 20 cm đến rất xa. Mắt người này mắc tật gì? Xác định giới hạn nhìn rõ của mắt người ấy khi không đeo kính?

Lời giải chi tiết:

Tiêu cự của thấu kính là: $\operatorname{f}=\frac{1}{D}=\frac{1}{-1,25}=-0,8\left( m \right)=-80\operatorname{cm}$

Vật ở rất xa tức là d =   cho ảnh d’ = f = -80 cm là ảnh ảo trước thấu kính (tức trước mắt) là 80 cm.

Vậy điểm cực viễn cách mắt 80 cm <   nên mắt đó là mắt cận thị.

Khi nhìn vật qua kính, ở cách mắt d = 20 cm thì sẽ cho ảnh ảo ở điểm cực cận nên ta có d’ = -OC_c.

Mà: $\frac{1}{f}=\frac{1}{d}+\frac{1}{d’}\Leftrightarrow \frac{1}{-80}=\frac{1}{20}-\frac{1}{O{{C}_{c}}}\Rightarrow \frac{1}{O{{C}_{c}}}=\frac{3}{80}\Rightarrow {{\operatorname{OC}}_{c}}=\frac{80}{3}\left( cm \right)=26,67\left( cm \right)$

Vậy giới hạn nhìn rõ của mắt người này là từ 26,67 cm đến 80 cm.

Bài tập 7: Mắt một người cận thị có khoảng cực cận là 12,5 cm và khoảng nhìn rõ của mắt là 37,5 cm. a) Hỏi người này phải đeo kính có độ tụ bằng bao nhiêu để nhìn rõ được các vật ở vô cực mà

không phải điều tiết? b) Người đó đeo kính có độ tụ như thế nào thì sẽ không nhìn thấy rõ được bất kì vật nào trước mắt? Coi kính đeo sát mắt.

 

Lời giải chi tiết:

a) Khoảng cách từ mắt đến điểm cực viễn: OC_v = 12,5 + 37,5 = 50 (cm)

Khi đeo kính nhìn vật ở vô cực thì cho ảnh ảo ở điểm cực viễn nên ta có: 

$\frac{1}{f}=\frac{1}{d}+\frac{1}{d’}=\frac{1}{\infty }+\frac{1}{-{{\operatorname{OC}}_{v}}}=-\frac{1}{50}\Rightarrow \operatorname{f}=-50\left( cm \right)=-0,5\left( m \right)$

Độ tụ của kính là: $\operatorname{D}=\frac{1}{f}=\frac{1}{-0,5}=-2\operatorname{dp}$

b) Để không nhìn thấy vật thì ảnh phải nằm ngoài phạm vi nhìn rõ của mắt.

Nếu kính là thấu kính hội tụ thì ảnh ảo sẽ nằm trước kính từ sát kính đến xa vô cùng tức là luôn có những vị trí của vật cho ảnh ảo nằm trong giới hạn nhìn rõ của mắt và mắt có thể nhìn rõ được các vật đó.

Với thấu kính phân kì ảnh của mọi vật là ảo nằm trong khoảng từ kính đến tiêu điểm ảnh F’ $\Rightarrow $Nếu F’ nằm bên trong điểm cực cận C_c thì mắt không thể nhìn rõ được bất cứ vật nào. Do đó ta có:

$\operatorname{OF}'<{{\operatorname{OC}}_{c}}\Leftrightarrow \left| f \right|<12,5\left( cm \right)=0,125\left( m \right)$

$\Leftrightarrow -0,125\left( m \right)<\operatorname{f}<0\Leftrightarrow -0,125\left( m \right)<\frac{1}{D}<0\Rightarrow \operatorname{D}<-8\operatorname{dp}$

Vậy, muốn không nhìn thấy rõ được bất kì vật nào trước mắt thì người này phải đeo kính phân kỳ có độ tụ thỏa mãn D < -8dp.

Bài tập 8: Một người cận thị có giới hạn nhìn rõ từ 20 cm đến 50 cm. Có thể sửa tật cận thị của người đó bằng hai cách: – Đeo kính cận L1 để có thể nhìn rõ vật ở rất xa. – Đeo kính cận L2 để có thể nhìn vật ở gần nhất là 25 cm. a) Hãy xác định số kính (độ tụ) của L1 và L2. b) Tìm khoảng cực cận khi đeo kính L1 và khoảng cực viễn khi đeo kính L2. c) Hỏi sửa tật cận thị theo cách nào có lợi hơn? Vì sao? Giả sử kính đeo sát mắt.

Lời giải chi tiết:

a) Khi đeo kính L₁: Qua L₁ vật ở vô cực cho ảnh ảo ở điểm cực viễn của mắt cận.

Như vậy: $\left\{ \begin{array}{} \operatorname{d}=\infty  \\ {} \operatorname{d}’=-{{\operatorname{OC}}_{v}}=-50\operatorname{cm} \\ \end{array} \right.\Rightarrow \frac{1}{{{\operatorname{f}}_{1}}}=\frac{1}{\infty }+\frac{1}{-50}\Rightarrow {{\operatorname{f}}_{1}}=-50\left( cm \right)=-0,5\left( m \right)$

Độ tụ của kính L₁ là: ${{\operatorname{D}}_{1}}=\frac{1}{{{f}_{1}}}=\frac{1}{-0,5}=-2\operatorname{dp}$

Khi đeo kínhL₂: Vật ở cách mắt 25cm cho ảnh ảo ở điểm cực cận của mắt

Như vậy: $\left\{ \begin{array}{} \operatorname{d}=25 \\ {} \operatorname{d}’=-{{\operatorname{OC}}_{c}}=-20\operatorname{cm} \\ \end{array} \right.\Rightarrow \frac{1}{{{\operatorname{f}}_{2}}}=\frac{1}{25}+\frac{1}{-20}\Rightarrow {{\operatorname{f}}_{2}}=-100\left( cm \right)=-1\left( m \right)$

Độ tụ của kính L₂ là: ${{\operatorname{D}}_{2}}=\frac{1}{{{f}_{2}}}=\frac{1}{-1}=-1\operatorname{dp}$

b) – Khoảng cực cận khi đeo kính L₁: vật chỉ có thể đặt gần mắt nhất ở vị trí cho ảnh ảo ở điểm cực cận của mắt. Như vậy: $\left\{ \begin{array}{} \operatorname{d}_{1}^{‘}=-20\text{cm} \\ {} {{\operatorname{f}}_{1}}=-50\text{cm} \\ \end{array} \right.\Rightarrow {{\operatorname{d}}_{1}}=\frac{d_{1}^{‘}{{f}_{1}}}{d_{1}^{‘}-{{f}_{1}}}=\frac{\left( -20 \right)\left( -50 \right)}{\left( -20 \right)-\left( -50 \right)}=33,3\text{cm}$

Vậy điểm gần nhất khi đeo kínhL₁ còn nhìn rõ vật cách mắt 33,3 cm

– Khoảng nhìn rõ xa nhất khi đeo kính L₂: vật chỉ có thể đặt xa mắt nhất ở vị trí cho ảnh ảo ở điểm cực viễn của mắt. Như vậy: $\left\{ \begin{array}{} \text{d}_{\text{2}}^{\text{ }\!\!’\!\!\text{ }}=-50\text{cm} \\ {} {{\text{f}}_{\text{2}}}=-100\text{cm} \\ \end{array} \right.\Rightarrow {{\text{d}}_{\text{2}}}=\frac{\text{d}_{\text{2}}^{\text{ }\!\!’\!\!\text{ }}{{\text{f}}_{\text{2}}}}{\text{d}_{\text{2}}^{\text{ }\!\!’\!\!\text{ }}-{{\text{f}}_{\text{2}}}}=\frac{\left( -50 \right)\left( -100 \right)}{\left( -50 \right)-\left( -100 \right)}=100\text{cm}$

Vậy điểm xa nhất khi đeo kính L₂ còn nhìn rõ vật cách mắt là 100 cm.

c) Khi đeo kính L₁ phạm vi nhìn từ 33,3 cm đến vô cùng, còn khi đeo kính L₂ phạm vi nhìn từ 25 cm đến 100 cm. Vậy đeo kính L₁ có lợi hơn.

Bài tập 9: Mắt viễn thị nhìn rõ được vật cách mắt gần nhất 40 cm. Tính độ tụ của kính phải đeo để có thể nhìn rõ vật đặt cách mắt gần nhất là 25 cm. Biết kính đeo sát mắt.

Lời giải chi tiết:

Theo đề ra ta có: OC_c = 40 cm

Khi đeo kính sát mắt, mắt nhìn thấy ảnh ảo của vật tại C_c.

Do đó: $\left\{ \begin{array}{} \text{d }\!\!’\!\!\text{ }=-\text{O}{{\text{C}}_{\text{c}}}=-40\left( \text{cm} \right) \\ {} \text{d}=25\left( \text{cm} \right) \\ \end{array} \right.$

Ta có: ${{\text{D}}_{\text{k}}}=\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}=\frac{1}{0,25}+\frac{1}{-0,4}=1,5\text{dp}\text{.}$

Bài tập 10: Một người chỉ nhìn rõ được các vật cách mắt từ 50 cm trở ra xa a) Mắt bị tật gì? b) Tính độ biến thiên độ tụ của thủy tinh thể khi người này quan sát các vật trong khoảng nhìn rõ của mắt. c) Người này phải đeo kính hội tụ hay phân kì, có độ tụ bao nhiêu để có thể nhìn rõ các vật ở

trước mắt  25 cm? Coi kính đeo sát mắt.

Lời giải chi tiết:

a) Mắt người này chỉ nhìn rõ được các vật cách mắt từ 50 cm trở ra xa nghĩa là có điểm cực cận C_c cách mắt 50 cm (OC_c > 25 cm) và có điểm cực viễn C_v ở vô cùng nên mắt người này bị viễn thị.

b) Sơ đồ tạo ảnh: 

Khi vật ở C_c: $\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}={{\text{D}}_{\text{1}}}\Leftrightarrow \frac{1}{\text{O}{{\text{C}}_{\text{c}}}}+\frac{1}{\text{OV}}={{\text{D}}_{\text{1}}}$

Khi vật ở C_v: $\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}={{\text{D}}_{\text{2}}}\Leftrightarrow \frac{1}{\text{O}{{\text{C}}_{\text{v}}}}+\frac{1}{\text{OV}}={{\text{D}}_{\text{2}}}$

Vậy độ biến thiên của độ tụ của thủy tinh thể là: $\Delta \text{D}={{\text{D}}_{\text{1}}}-{{\text{D}}_{\text{2}}}=\frac{1}{\text{O}{{\text{C}}_{\text{c}}}}-\frac{1}{\text{O}{{\text{C}}_{\text{v}}}}=\frac{1}{0,5}-\frac{1}{\infty }=2\text{dp}$

c) Vì mắt người này bị viễn thị nên cần đeo kính hội tụ sao cho khi nhìn vật ở cách mắt 25 cm thì cho ảnh ảo ở điểm cực cận của mắt.

Ta có: $\frac{1}{{{\text{f}}_{\text{k}}}}=\frac{1}{\text{d}}+\frac{1}{\text{d }\!\!’\!\!\text{ }}=\frac{1}{\text{d}}+\frac{1}{-\text{O}{{\text{C}}_{\text{c}}}}=\frac{1}{25}+\frac{1}{-50}\Rightarrow {{\text{f}}_{\text{k}}}=50\left( \text{cm} \right)$

Vậy người này phải đeo kính hội tụ có độ tụ là: