Dạng 1: Cho khoảng thời gian $\text{ }\!\!\Delta\!\!\text{ t}$, tìm trạng thái trước hoặc sau đó
1. ĐẶT VẤN ĐỀ
Xét bài toán: Một vật dao động điều hòa với phương trình $\text{x=Acos}\left( \text{ }\!\!\omega\!\!\text{ t+ }\!\!\varphi\!\!\text{ } \right)$. Tính từ thời điểm t1, sau (hoặc trước) một khoảng thời gian $\text{ }\!\!\Delta\!\!\text{ t}$vật có trạng thái như thế nào?
2. PHƯƠNG PHÁP GIẢI
Cách 1: Sử dụng phương pháp đường tròn lượng giác.
+) Tại thời điểm t1, trạng thái của vật là $({{x}_{1}};{{v}_{1}})\Rightarrow $pha dao động là ${{\varphi }_{1}}\left( {{\varphi }_{1}}\in \left[ -\pi ;\pi \right] \right)$.
(Vận tốc dương ta lấy $-\pi <{{\varphi }_{1}}<0$; vận tốc âm ta lấy $0<{{\varphi }_{1}}<\pi $).
+) Trong khoảng thời gian $\text{ }\!\!\Delta\!\!\text{ t}$vật quét được một góc là $\Delta \varphi =\omega .\Delta t$.
Khi đó suy ra pha dao động ở thời điểm trước hoặc sau một khoảng thời gian $\text{ }\!\!\Delta\!\!\text{ t}$ là ${{\varphi }_{2}}={{\varphi }_{1}}\mp \Delta \varphi $. (trước là dấu trừ, sau là dấu cộng).
+) Từ đó suy ra trạng thái trước hoặc sau đó của vật.
Chú ý: Ta có thể thêm bớt một lượng $k2\pi $ để tính toán dễ dàng hơn: ${{\varphi }_{2}}={{\varphi }_{1}}\mp \Delta \pm k2\pi $. (không thêm bớt vẫn được).
Cách 2: Sử dụng trục thời gian.
Tại thời điểm t1, trạng thái của vật là $({{x}_{1}};{{v}_{1}})$.
Tách $\Delta \text{T = nT + }\!\!\Delta\!\!\text{ {t}’}$với $n\in N,\Delta {t}’$< T.
Sau n chu kì, vật trở về trạng thái như cũ. Dựa vào $\text{ }\!\!\Delta\!\!\text{ {t}’}$để tìm trạng thái cần tìm của vật.
1. BÀI TẬP MINH HỌA DẠNG 1
|
Bài tập 1: Một vật nhỏ thực hiện dao động điều hòa theo phương trình $x=10\cos \left( 4\pi t-\frac{\pi }{3} \right)$cm. Tại thời điểm t1, vật có li độ $5\sqrt{2}$cm và đang giảm. Li độ của vật sau thời điểm đó $\frac{7}{48}$s là A. $x=-5\sqrt{2}$cm B. $x=-5$cm C. $x=-5\sqrt{3}$cm D. $x=5\sqrt{2}$cm |
Lời giải chi tiết
Tại thời điểm t1, ta có: $\left\{ \begin{array}{} 5\cos {{\varphi }_{1}}=5\sqrt{2} \\ {} x\downarrow \\ \end{array} \right.\Rightarrow {{\varphi }_{1}}=\frac{\pi }{4}$.
Lại có: $\Delta \varphi =\omega \Delta t=4\pi .\frac{7}{48}$suy ra ${{\varphi }_{2}}=\Delta \varphi +{{\varphi }_{1}}=\frac{5\pi }{6}\Rightarrow {{x}_{2}}=10\cos \frac{5\pi }{6}=-5\sqrt{3}$. Chọn C.
|
Bài tập 2: Một vật dao động điều hòa với phương trình $x=4\sqrt{2}\cos \left( 4\pi t-\frac{2\pi }{3} \right)$(cm). Tại một thời điểm nào đó vật đang có li độ $x=-4$cm và đang tăng, sau đó khoảng thời gian là $\Delta t=0,229$s gia tốc của vật là: A. 7,74 m/s2 B. –7,74 m/s2 C. 4,47 m/s2 D. –4,47 m/s2 |
Lời giải chi tiết
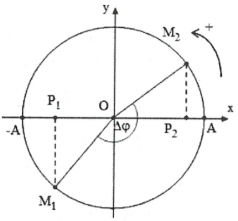
Tại thời điểm t ta có: $\left\{ \begin{array}{} x=-4\text{ cm} \\ {} x\uparrow \\ \end{array} \right.$suy ra
${{\varphi }_{0}}=\frac{-3\pi }{4}$. Sau $\Delta t=0,223$s vật quét được một góc là $\Delta \varphi =0,223.4\pi =2,8777$rad.
Do đó ${{\varphi }_{1}}={{\varphi }_{0}}+\Delta \varphi =0,5215$rad.
$\Rightarrow \text{a}=-{{\omega }^{2}}x=-16{{\pi }^{2}}.4\sqrt{2}\cos 0,5215=-7,74$m/s2.
Chọn B.
|
Bài tập 3: Một vật dao động điều hòa với phương trình $x=10\cos \left( 4\pi t-\frac{\pi }{4} \right)$(cm). Tại thời điểm nào đó vật đang có li độ $x=4$cm và đang ra xa vị trí cân bằng. Trước đó 3,25s vật đang: A. có li độ $x=-4$cm và chuyển động theo chiều âm B. có li độ $x=-4$cm và chuyển động theo chiều dương C. có li độ $x=4$cm và chuyển động theo chiều âm D. có li độ $x=4$cm và chuyển động theo chiều dương |
Lời giải chi tiết
Tại thời điểm t ta có: $\left\{ \begin{array}{} 10\cos {{\varphi }_{1}}=4 \\ {} x\uparrow \Rightarrow \varphi \text{ }0 \\ \end{array} \right.\Rightarrow {{\varphi }_{1}}=-\text{arccos}0,4=-1,159\text{ (rad)}$.
Trong thời gian $\Delta t=3,25s$vật quét được một góc là $\Delta \varphi =\omega .\Delta t=3,25.4\pi =13\pi \text{ (rad)}$.
Do đó ${{\varphi }_{0}}={{\varphi }_{1}}-\Delta \varphi =-\text{arccos}0,4-13\pi \Rightarrow \left\{ \begin{array}{} x=10\cos {{\varphi }_{0}}=-4 \\ {} v=-\omega A\sin {{\varphi }_{0}}\text{}0 \\ \end{array} \right.$.
Vật có li độ $x=-4$cm và chuyển động theo chiều âm. Chọn A.
|
Bài tập 4: Một vật dao động điều hòa với phương trình $x=8\cos \left( \frac{4\pi }{3}t+\frac{\pi }{6} \right)$(cm). Tại một thời điểm nào đó vật đang có li độ $x=4\sqrt{3}$ và đang tăng. Sau khoảng thời gian là $\Delta t=5,125$s li độ và vận tốc của vật lần lượt là: A. $x=-4\sqrt{2}\text{ cm; v = }\frac{8\pi \sqrt{2}}{3}\text{cm / s}$ B. $x=-4\sqrt{2}\text{ cm; v =}-\frac{8\pi \sqrt{2}}{3}\text{cm / s}$ C. $x=-4\text{ cm; v = }8\pi \sqrt{3}\text{ cm / s}$ D. $x=-4\text{ cm; v = }-\frac{8\pi \sqrt{3}}{3}\text{cm / s}$ |
Lời giải chi tiết
Tại thời điểm $\left\{ \begin{array}{} x=4\sqrt{3} \\ {} \text{v 0} \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{} \text{cos}\varphi \text{=}\frac{\sqrt{3}}{2} \\ {} \text{v 0} \\ \end{array} \right.\Rightarrow \varphi =-\frac{\pi }{6}$.
Sau khoảng thời gian $\Delta t=5,125s$vật quét được góc $\Delta \varphi =\omega .\Delta t=\frac{4\pi }{3}.5,125=\frac{41}{6}\pi \text{ (rad)}$
Khi đó ${{\varphi }_{2}}={{\varphi }_{1}}+\Delta \varphi =\frac{20\pi }{3}.$Khi đó $\left\{ \begin{array}{} x=8\cos \frac{20\pi }{3}=-4 \\ {} v=-\frac{16\pi }{3}\sin \frac{20\pi }{3}=\frac{-8\pi \sqrt{3}}{3}\text{ cm/s} \\ \end{array} \right.$. Chọn D.
|
Bài tập 5: Một vật dao động điều hòa với phương trình $x=2\cos \left( 2\pi t-\frac{\pi }{6} \right)$(cm). Tại một thời điểm nào đó vật đang có li độ x = 1 cm và đang chuyển động theo chiều âm. Li độ và vận tốc của vật sau đó khoảng thời gian $\Delta t=\frac{17}{12}\text{s}$ A. $x=-3\text{ cm; v = }2\pi \text{ cm / s}$ B. $x=-\sqrt{3}\text{ cm; v =}-2\pi \text{ cm / s}$ C. $x=-1\text{ cm; v = }2\pi \sqrt{3}\text{ cm / s}$ D. $x=-1\text{ cm; v =}-2\pi \sqrt{3}\text{ cm / s}$ |
Lời giải chi tiết
Tại thời điểm $\left\{ \begin{array}{} x=1 \\ {} v<0 \\ \end{array} \right.\Rightarrow {{\varphi }_{1}}=\frac{\pi }{3}$.
Sau khoảng thời gian $\Delta t=\frac{17}{12}\text{s}$ vật quét được một góc là $\Delta \varphi =\omega .\Delta t=2\pi +\frac{5}{6}\pi $.
Suy ra ${{\varphi }_{2}}={{\varphi }_{1}}+\Delta \varphi =4\pi -\frac{5\pi }{6}$.
Do đó $\left\{ \begin{array}{} x=2\cos \left( -\frac{5\pi }{6} \right)=-\sqrt{3}\text{ cm} \\ {} v=-4\pi \sin \left( -\frac{5\pi }{6} \right)=2\pi \text{ cm/s} \\ \end{array} \right.$. Chọn A.
|
Bài tập 6: Một vật dao động điều hòa với phương trình $x=10\cos \left( \frac{4\pi t}{3}-\frac{\pi }{4} \right)$(cm). Tại một thời điểm t1 vật đang có li độ $x=6$ cm và đang chuyển động ra xa vị trí cân bằng. Sau đó khoảng thời gian 4,125s vật đang A. Có li độ $x=8$cm và chuyển động theo chiều dương B. Có li độ $x=8$cm và chuyển động theo chiều âm C. Có li độ $x=-8$cm và chuyển động theo chiều dương D. Có li độ $x=-8$cm và chuyển động theo chiều âm |
Lời giải chi tiết
Tại thời điểm t1 ta có $\left\{ \begin{array}{} x=6\text{ cm} \\ {} \text{v 0} \\ \end{array} \right.\Rightarrow {{\varphi }_{1}}=-\text{arccos}\frac{6}{10}=-0,927\text{ rad}$.
Sau khoảng thời gian 4,125s vật quét được góc $\Delta \varphi =\omega .\Delta t=\frac{11\pi }{2}$
Suy ra ${{\varphi }_{2}}={{\varphi }_{1}}+\Delta \varphi =\frac{11\pi }{2}-\text{arccos}\frac{6}{10}$.
Do đó $\left\{ \begin{array}{} x=10\cos {{\varphi }_{2}}=-8 \\ {} v=-\frac{40\pi }{3}\sin {{\varphi }_{2}}=8\pi \text{ cm/s} \\ \end{array} \right.$. Chọn C.
|
Bài tập 7: Một vật dao động điều hòa với chu kỳ là T. Tại một thời điểm t1 tỉ số vận tốc và li độ là $\frac{{{v}_{1}}}{{{x}_{1}}}=\frac{\omega }{\sqrt{3}}$. Tại thời điểm ${{t}_{2}}={{t}_{1}}+\Delta t$ thì tỉ số đó là $\frac{{{v}_{2}}}{{{x}_{2}}}=-\omega \sqrt{3}$. Giá trị nhỏ nhất của $\Delta t$là A. $\frac{T}{6}$ B. $\frac{T}{3}$ C. $\frac{T}{12}$ D. $\frac{T}{4}$ |
Lời giải chi tiết
$\frac{{{v}_{1}}}{{{x}_{1}}}=\frac{\omega }{\sqrt{3}}\Rightarrow \left\{ \begin{array}{} \frac{v_{1}^{2}}{x_{1}^{2}}=\frac{{{\omega }^{2}}}{3}\Leftrightarrow \frac{{{\omega }^{2}}\left( {{A}^{2}}-x_{1}^{2} \right)}{x_{1}^{2}}=\frac{{{\omega }^{2}}}{3}\Leftrightarrow {{A}^{2}}=\frac{4}{3}x_{1}^{2}\Rightarrow {{x}_{1}}=\pm \frac{A\sqrt{3}}{2} \\ {} {{x}_{1}}{{v}_{1}}>0\text{ }\left( \text{do }\omega \text{ 0} \right) \\ \end{array} \right.$ứng với M1, M2.
Tương tự$\frac{{{v}_{2}}}{{{x}_{2}}}=-\omega \sqrt{3}\Rightarrow \left\{ \begin{array}{} {{x}_{2}}=\pm \frac{A}{2} \\ {} {{x}_{2}}{{v}_{2}}<0\text{ }\left( \text{do }\omega \text{ 0} \right) \\ \end{array} \right.$ ứng với N1, N2.
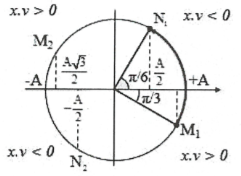
Khoảng thời gian nhỏ nhất đi từ trạng thái 1 đến trạng thái 2: $\widehat{{{M}_{1}}{{N}_{1}}}=\frac{\pi }{2}\Rightarrow \Delta t=\frac{T}{4}$. Chọn D.
