CÁCH GIẢI CÁC DẠNG BÀI DAO ĐỘNG TẮT DẦN, DAO ĐỘNG CƯỠNG BỨC
Dạng 1. Bài toán liên quan đến hiện tượng cộng hưởng cơ
| Bài tập 1: [Trích đề thi đại học năm 2009]. Khi nói về dao động cưỡng bức, phát biểu nào sau đây là đúng?
A. Dao động cưỡng bức có biên độ không đổi và có tần số bằng tần số của lực cưỡng bức. B. Dao động của con lắc đồng hồ là dao động cưỡng bức. C. Dao động cưỡng bức có tần số nhỏ hơn tần số của lực cưỡng bức. D. Biên độ của dao động cưỡng bức là biên độ của lực cưỡng bức. |
Lời giải chi tiết:
A đúng dao động cưỡng bức có biên độ không đổi (ở giai đoạn ổn định) và có tần số bằng tần số của lực cưỡng bức.
B sai vì dao động của con lắc đồng hồ là dao động duy trì.
C sai vì dao động cưỡng bức có tần số bằng tần số của lực cưỡng bức.
D sai vì dao động cưỡng bức có biên độ thay đổi và đạt cực đại khi tần số lực cưỡng bức bằng tần số riêng của hệ dao động. Chọn A.
Bài tập 2: Khảo sát thực nghiệm một con lắc lò xo gồm vật nhỏ có khối lượng 216 g và lò xo có độ cứng k, dao động dưới tác dụng của ngoại lực $F={{F}_{0}}\cos 2\pi ft$, với F0 không đổi và f thay đổi được. Kết quả khảo sát ta được đường biểu diễn biên độ A của con lắc theo tần số f có đồ thị như hình vẽ. Giá trị của k xấp xỉ bằng 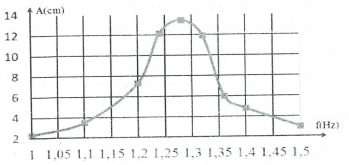
A. 13,64 N / m. B. 12,35 N / m. C. 15,64 N / m. D. 16,71 N / m. |
Lời giải chi tiết:
Khi biên độ của con lắc đạt giá trị lớn nhất khi xảy ra cộng hưởng.
Khi đó $f={{f}_{0}}=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\Rightarrow k=m{{\left( 2\pi {{f}_{0}} \right)}^{2}}.$
Dựa vào đồ thị ta thấy biên độ A cực đại khi $f={{f}_{0}}\approx 1,28\Rightarrow k\approx 13,97$N. Chọn A.
| Bài tập 3: Một con lắc đơn có chiều dài 16 cm dao động trong không khí. Cho g = 10 m/s2 và ${{\pi }^{2}}=10$. Tác dụng lên con lắc một ngoại lực biến thiên tuần hoàn với biên độ có giá trị không đổi, nhưng tần số f có thể thay đổi được. Khi tần số của ngoại lực lần lượt có giá trị f1 = 0,7 Hz và f2 = 1,5 Hz thì biên độ dao động của vật tương ứng là A1 và A2. Kết luân nào dưới đây là đúng?
A. ${{\Alpha }_{1}}\ge {{\Alpha }_{2}}.$ B. ${{\Alpha }_{1}}>{{\Alpha }_{2}}.$ C. ${{\Alpha }_{1}}<{{\Alpha }_{2}}.$ D. ${{\Alpha }_{1}}={{\Alpha }_{2}}.$ |
Lời giải chi tiết:
Tần số dao động riêng (tần số cộng hưởng): $f=2\pi \sqrt{\frac{1}{g}}=1,25Hz$
Vì f2 gần f hơn nên $\Rightarrow {{\Alpha }_{1}}<{{\Alpha }_{2}}.$ Chọn C.
| Bài tập 4: Một con lắc lò xo gồm một viên bi khối lượng nhỏ 100 g và lò xo nhẹ có độ cứng 10 N/m. Con lắc dao động cưỡng bức dưới tác dụng của ngoại lực tuần hoàn có tần số góc$\omega $. Biết biên độ của ngoại lực cưỡng bức không thay đổi. Khi thay đổi $\omega $tăng dần từ 9 rad/s đến 12 rad/s thì biên độ dao động của viên bi
A. giảm đi 3/4 lần. B. tăng lên sau đó lại giảm. C. tăng lên 4/3 lần. D. giảm rồi sau đó tăng. |
Lời giải chi tiết:
Tần số góc riêng của hệ ${{\omega }_{0}}=\sqrt{\frac{k}{m}}=\sqrt{\frac{10}{0,1}}=10$rad /s
Xảy ra cộng hưởng khi $\omega ={{\omega }_{0}}=10rad/s\Rightarrow $khi tăng dần số góc $\omega $ của ngoại lực cưỡng bức từ 9 rad/s đến 12 rad/s thì tại $\omega ={{\omega }_{0}}=10$rad/s hệ xảy ra cộng hưởng, biên độ dao động của viên bi lớn nhất $\Rightarrow $biên độ dao động viên bi tăng đến cực đại rồi giảm khi thay đổi $\omega $. Chọn B.
| Bài tập 5: [Trích đề thi THPTQG năm 2017]. Một con lắc lò xo có độ cứng 100 N /m và vật nhỏ có khối lượng m. Tác dụng lên vật ngoại lực $F=20\cos 10\pi t\left( N \right)$(t tính bằng giây) dọc theo trục Ox thì xảy ra hiện tượng cộng hưởng. Lấy${{\pi }^{2}}=10$. Giá trị của m là
A. 100 g. B. 1 kg. C. 250 g. D. 0,4 kg. |
Lời giải chi tiết:
Do xảy ra hiện tưởng cộng hưởng nên ta có: f = f0
Trong đó f là tần số của ngoại lực và $f=\frac{\omega }{2\pi }=5$ Hz.
f0 là tần số riêng cuủa hệ: ${{f}_{0}}=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\Rightarrow \frac{1}{2\pi }\sqrt{\frac{k}{m}}=5\Rightarrow \frac{k}{m}=1000\Rightarrow m=0,1$kg. Chọn A.
| Bài tập 6: Một xe ô tô chạy trên đường, cứ cách 6 m lại có một cái mô nhỏ. Chu kì dao động tự do của khung xe trên các lò xo là 1,5 s. Xe chạy với vận tốc nào thì bị rung mạnh nhất
A. 4 m / s. B. 2 m / s. C. 8 m / s. D. 5,33 m / s. |
Lời giải chi tiết:
Cứ 6 m lại có một cái mô nhỏ làm xe rung. Chu kì của ngoại lực chính bằng thời gian 2 lần liên tiếp xe gặp cái mô nhỏ. Suy ra $\Tau =\frac{S}{v}.$
Chu kì riêng của khung xe trên các lò xo là Triêng =1,5 s.
Để xe rung mạnh nhất khi xảy ra cộng hưởng suy ra ${{\Tau }_{F}}={{\Tau }_{rieng}}\Rightarrow v=\frac{6}{1,5}=4m/s.$
Chọn A.
| Bài tập 7: Một hành khách dùng dây chằng cao su treo một chiếc ba lô trên trần toa tàu, ngay phía trên một trục bánh xe của toa tàu. Khối lượng của ba lô là 16 kg, hệ số cứng của dây chằng cao su là 900 N/m. Chiều dài mỗi thanh ray là 12,5 m, ở chỗ nối thanh ray có một khe hở nhỏ. Để ba lô dao động mạnh nhất thì tàu phải chạy với vận tốc là
A. v = 54 km / h. B. v = 27 km / h. C. v = 54 m / s. D. v = 27 m / h. |
Lời giải chi tiết:
Để ba lô rung mạnh nhất thì chu kì riêng của dây chằng cao su bằng chu kì của ngoại lực. Khi đó
$2\pi \sqrt{\frac{m}{k}}=\frac{s}{v}\Rightarrow v=14,92m/s\approx 54km/h.$ Chọn A.
Dạng 2. Bài tập liên quan dao động tắt dần
a.) Dao động tắt dần
+) Cơ năng $\text{W}=\frac{1}{2}k{{\Alpha }^{2}}$
+) Mối quan hệ giữa độ giảm năng lượng và độ giảm biên độ sau 1 chu kì:
Ta có: $\Rightarrow =\frac{\left( \Alpha +{\Alpha }’ \right)\left( \Alpha -{\Alpha }’ \right)}{{{\Alpha }^{2}}}$
Làm gần đúng: $\Alpha +{\Alpha }’=2\Alpha \Rightarrow $
+) Phần trăm biên độ bị giảm sau n chu kì:${{h}_{\left( \Alpha \right)n}}=\frac{\Alpha -{{\Alpha }_{n}}}{\Alpha }$
+) Phần trăm cơ năng còn lại sau n chu kì: ${{h}_{\left( \text{W} \right)n}}=\frac{{{\text{W}}_{n}}}{\text{W}}={{\left( \frac{\Alpha {}_{n}}{\Alpha } \right)}^{2}}$
+) Sau 1 chu kì biên độ giảm a% thì sau n chu kì biên độ của vật là: ${{\Alpha }_{n}}={{\left( 1-a% \right)}^{n}}\Alpha .$
| Bài tập 1: Một vật dao động tắt dần có các đại lượng giảm liên tục theo thời gian là:
A. biên độ và năng lượng . B. li độ và tốc độ. C. biên độ và tốc độ. D. biên độ và gia tốc. |
Lời giải chi tiết:
Dao động có biên độ giảm dần theo thời gian gọi là dao động tắt dần.
Do đó biên độ và năng lượng giảm dần theo thời gian. Chọn A.
| Bài tập 2: [Trích đề thi THPTQG năm 2017]. Khi nói về dao động tắt dần của một vật, phát biểu nào sau đây là đúng.
A. Li độ của vật luôn giảm dần theo thời gian. B. Gia tốc của vật luôn giảm dần theo thời gian. C. Vận tốc của vật luôn giảm dần theo thời gian. D. Biên độ dao động của vật giảm dần theo thời gian. |
Lời giải chi tiết:
Trong dao động tắt dần, biên độ dao động và cơ năng của vật giảm dần theo thời gian. Chọn D.
| Bài tập 3: Nguyên nhân gây ra dao động tắt dần của con lắc đơn trong không khí là:
A. Do trọng lực tác dụng lên vật. B. Do lực căng của dây treo. C. Do lực cản của môi trường. D. Do khối lượng của dây treo. |
Lời giải chi tiết:
Nguyên nhân gây ra dao động tắt dần của con lắc đơn trong không khí là do lực cản của không khí.
Chọn C.
| Bài tập 4: Nhận định nào sau đây là sai khi nói về dao động cơ tắt dần.
A. Dao động tắt dần là dao động có biên độ giảm dần theo thời gian. B. Lực ma sát càng lớn thì dao động tắt dần càng nhanh. C. Trong dao động tắt dần cơ năng của vật giảm dần theo thời gian. D. Dao động tắt dần có động năng giảm dần còn thế năng biến thiên điều hòa. |
Lời giải chi tiết:
Đáp án sai là D. Chọn D.
| Bài tập 5: [Trích đề thi THPTQG năm 2017]. Một con lắc lò xo dao động tắt dần trên mặt phẳng nằm ngang. Cứ sau mỗi chu kì biên độ giảm 2%. Gốc thế năng tại vị trí mà lò xo không bị biến dạng. Phần trăm cơ năng con lắc bị mất đi trong hai dao động toàn phần liên tiếp có giá trị gần nhất với giá trị nào sau đây. A. 7%. B. 4%. C. 10%. D. 8%. |
Lời giải chi tiết:
Cách 1: Làm thuần túy: Giả sử biên độ ban đầu là A.
Sau 1 chu kì biên độ con lắc còn A1 = 0,98A, sau 2 chu kì biên độ con lắc còn
${{\Alpha }_{2}}=0,98{{\Alpha }_{1}}=0,{{98}^{2}}\Alpha $suy ra $\frac{\text{W}-{{\text{W}}_{2}}}{\text{W}}=1-\frac{\Alpha _{2}^{2}}{{{\Alpha }^{2}}}=1-0,{{98}^{4}}\approx 7,76%.$
Cách 2: Làm theo công thức gần đúng: $\frac{\Delta \text{W}}{\text{W}}=\frac{2\Delta \Alpha }{\Alpha }=4%$.
Công thức trên là công thức xấp xỉ độ giảm cơ năng trong một chu kì.
Do đó trong 2 chu kì liên tiếp cơ năng sẽ giảm 2.4% = 8%. Chọn D.
| Bài tập 6: [Trích đề thi chuyên Hạ Long – Quảng Ninh năm 2017]. Cơ năng của một dao động tắt dần chậm giảm 5% sau mỗi chu kì. Phần trăm biên độ giảm sau mỗi chu kì có giá trị gần giá trị nào nhất sau đây ?
A. 5%. B. 2,5%. C. 2,24%. D. 10%. |
Lời giải chi tiết:
$\frac{\Delta \text{W}}{\text{W}}=\frac{2\Delta \Alpha }{\Alpha }=5%\Rightarrow \frac{\Delta \Alpha }{\Alpha }=2,5%.$Chọn B.
| Bài tập 7: Một con lắc dao động tắt dần. Cứ sau mỗi chu kì, biên độ giảm 2%. Phần năng lượng của con lắc bị mất đi trong một dao động toàn phần là
A. 4,5%. B. 4%. C. 9,81%. D. 3,96%. |
Lời giải chi tiết:
Cách 1: $\frac{\Delta \text{W}}{\text{W}}=1-\frac{{{{{\Alpha }’}}^{2}}}{{{\Alpha }^{2}}}=1-{{\left( \frac{0,98\Alpha }{\Alpha } \right)}^{2}}=3,96%$.
Cách 2: gần đúng $\frac{\Delta \text{W}}{\Alpha }=\frac{2\Delta \Alpha }{\Alpha }=4%$.
Do vậy bài này không được áp dụng công thức gần đúng. Chọn D.
| Bài tập 8: Một con lắc lò xo đang dao động tắt dần, sau ba chu kì đầu tiên biên độ của nó giảm đi 10%. Phần trăm cơ năng còn lại sau khoảng thời gian đó là
A. 6,3%. B. 81%. C. 19%. D. 27%. |
Lời giải chi tiết:
$\left\{ \begin{array}{} \frac{\Alpha -{{\Alpha }_{3}}}{\Alpha }=10%\Rightarrow \frac{{{\Alpha }_{3}}}{\Alpha }=90% \\ {} \frac{{{\text{W}}_{3}}}{\text{W}}={{\left( \frac{\Alpha {}_{3}}{\Alpha } \right)}^{2}}=0,{{9}^{2}}=0,81=81% \\ \end{array} \right..$ Chọn B.
| Bài tập 9: Một con lắc dao động tắt dần chậm. Cứ sau mỗi chu kì, biên độ giảm 2% so với lượng còn lại. Sau 5 chu kì, so với năng lượng ban đầu, năng lượng còn lại của con lắc bằng
A. 74,4%. B. 18,47%. C. 25,6%. D. 81,7%. |
Lời giải chi tiết:
Sau 5T thì biên độ là${{\Alpha }_{5}}={{\left( 0,98 \right)}^{5}}\Alpha $
$\Rightarrow \frac{{{\text{W}}_{5}}}{\text{W}}={{\left( \frac{\Alpha {}_{5}}{\Alpha } \right)}^{2}}={{\left( 0,{{98}^{5}} \right)}^{2}}.100%=81,7%.$ Chọn D.
b) Dao động tắt dần của con lắc lò xo nằm ngang.
Ta chỉ xét dao động tắt dần chậm nên độ giảm biên độ sau một chu kì rất nhỏ:
$\Delta \Alpha =\Alpha -{\Alpha }’\Rightarrow \Alpha +{\Alpha }’\approx 2\Alpha $
Độ giảm cơ năng sau một chu kì bằng công thức của lực ma sát thực hiện trong chu kì đó:
$\frac{k{{\Alpha }^{2}}}{2}-\frac{k{{{{\Alpha }’}}^{2}}}{2}={{F}_{ms}}.4\Alpha \Leftrightarrow \frac{k}{2}\left( \Alpha +{\Alpha }’ \right)\left( \Alpha -{\Alpha }’ \right)={{F}_{ms}}.4\Alpha \Rightarrow \Delta \Alpha =\frac{4{{F}_{ms}}}{k}=\frac{4\mu mg}{k}$
+) Độ giảm biên độ sau mỗi chu kì:$\Delta \Alpha =\frac{4{{F}_{ms}}}{k}=\frac{4\mu mg}{k}$
+) Độ giảm biên độ sau nửa chu kì: $\frac{\Delta \Alpha }{2}=\frac{2{{F}_{ms}}}{k}=\frac{2\mu mg}{k}$
+) Biên độ dao động còn lại sau n chu kì:${{\Alpha }_{n}}=\Alpha -n\Delta \Alpha $
+) Tổng số dao động thực hiện được: $\Nu =\frac{\Alpha }{\Delta \Alpha }=\frac{k\Alpha }{4\mu mg}=\frac{{{\omega }^{2}}\Alpha }{4\mu g}$
+) Tổng quãng đường và tổng thời gian từ lúc bắt đầu dao động cho đến khi dừng hẳn lần lượt là:
$\left\{ \begin{array}{} \frac{1}{2}k{{\Alpha }^{2}}={{F}_{ms}}S\Rightarrow S=\frac{k{{\Alpha }^{2}}}{2\mu mg}=\frac{{{\omega }^{2}}{{\Alpha }^{2}}}{2\mu g} \\ {} t=\Nu .\Tau =\Nu .\frac{2\pi }{\omega } \\ \end{array} \right.$ (áp dụng định luật bảo toàn năng lượng)
+) Tốc độ trung bình trong cả quá trình dao động là:$\left| \overrightarrow{v} \right|=\frac{S}{t}=\frac{\omega \Alpha }{\pi }.$
+) Vận tốc lớn nhất trong dao động tắt dần: Vật sẽ đạt vận tốc lớn nhất khi vật qua vị trí cân bằng và ở trong nửa chu kì đầu tiên. Có 2 cách để giải bài toán này.
Cách 1: Áp dụng theo dao động điều hòa.
Ta có: ${{v}_{\max 1}}=\omega {\Alpha }’$với ${\Alpha }’=\frac{\Alpha +{{\Alpha }_{1}}}{2}$(${\Alpha }’$bằng một nửa quãng đường dao động trong nửa chu kì đầu).
Mặt khác ${\Alpha }’=\frac{\Alpha +{{\Alpha }_{1}}}{2}=\frac{2\Alpha -2\frac{\mu mg}{k}}{2}=\Alpha -\frac{\mu mg}{k}.$
Suy ra ${{v}_{\max 1}}=\omega {\Alpha }’=\omega \left( \Alpha -\frac{\mu mg}{k} \right).$
Cách 2: Áp dụng định luật bảo toàn năng lượng trong quá trình dao động.
$\frac{1}{2}k{{\Alpha }^{2}}=\frac{1}{2}kx_{0}^{2}+\frac{1}{2}mv_{\max }^{2}+\mu mg\left( \Alpha -{{x}_{0}} \right)$(với${{x}_{0}}=\frac{\mu mg}{k}$).
Suy ra $k{{\Alpha }^{2}}=kx_{0}^{2}+mv_{\max }^{2}+2k\left( \Alpha -{{x}_{0}} \right)\Rightarrow k{{\left( \Alpha -{{x}_{0}} \right)}^{2}}=mv_{\max }^{2}\Rightarrow {{v}_{\max }}=\omega \left( \Alpha -{{x}_{0}} \right).$
Khảo sát chi tiết:
+) Sự thay đổi vị trí cân bằng:
Con lắc lò xo chuyển động trên phương nằm ngang. Khi có lực ma sát tác động vào vật sẽ làm cho vị trí cân bằng của vật dịch chuyển.
Gọi x0 là tọa độ của vtcb mới. Tại vtcb mới:$\overrightarrow{{{F}_{dh}}}=-\overrightarrow{{{F}_{ms}}}\Rightarrow \left\{ \begin{array}{} {{F}_{dh}}={{F}_{ms}}\left( 1 \right) \\ {} \overrightarrow{{{F}_{dh}}}\uparrow \downarrow \overrightarrow{{{F}_{ms}}}\left( 2 \right) \\ \end{array} \right.$
(1) $\Leftrightarrow k\left| {{x}_{0}} \right|=\mu mg\Rightarrow \left| {{x}_{0}} \right|=\frac{\mu mg}{k}$
(2) Lực ma sát phụ thuộc vào chiều chuyển động của vật. Trong một dao động, con lắc chuyển động theo 2 chiều nên lực ma sát tương ứng theo 2 chiều là khác nhau.
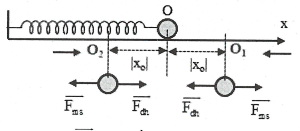
Vật chuyển động từ phải sang trái $\Rightarrow \overrightarrow{{{F}_{ms}}}$có chiều từ trái qua phải. Tại vtcb O1, $\overrightarrow{{{F}_{dh}}}$hướng từ phải qua trái: lò xo đang giãn ${{x}_{01}}=\frac{\mu mg}{k}={{x}_{0}}>0.$
Vật chuyển động từ trái sang phải $\Rightarrow \overrightarrow{{{F}_{ms}}}$có chiều từ phải sang trái. Tại vtcb O2, $\overrightarrow{{{F}_{dh}}}$hướng từ trái qua phải: lò xo đang nén ${{x}_{02}}=-\frac{\mu mg}{k}=-{{x}_{0}}<0.$
$\Rightarrow $Hai vtcb đối xứng nhau qua vị trí lò xo tự nhiên O, cách O một đoạn: $\left| {{x}_{0}} \right|=\frac{\mu mg}{k}.$
+) Tìm vị trí vật dừng lại:
Xét trong một nửa chu kì 2 vị trí biên đối xứng nhau qua vtcb O1 hoặc O2. Và sau mỗi lần đi qua O, biên độ lại giảm một lượng $\frac{\Delta \Alpha }{2}=\frac{2\mu mg}{k}=-2{{x}_{0}}.$
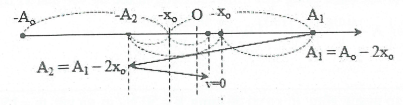
Vị trí vật dừng lại sẽ là biên (v = 0). Mặt khác, ta dễ dàng chứng minh được trong đoạn $\left[ -{{x}_{\circ }},{{x}_{\circ }} \right],$lực ma sát trượt lớn hơn lực đàn hồi của lò xo, nên trong đoạn này vật chuyển động chậm dần. Nếu vật dừng lại biên ${{\Alpha }_{n}}\in $đoạn $\left[ -{{x}_{\circ }},{{x}_{\circ }} \right],$nó sẽ dừng lại mãi mãi vì khi đó lực ma sát nghỉ cân bằng với lực đàn hồi.
Tổng số lần vật đi qua O cho đến biên cuối cùng ngoài $\left[ -{{x}_{\circ }},{{x}_{\circ }} \right]$là:
$\Nu =\left[ \frac{{{\Alpha }_{\circ }}}{2{{x}_{\circ }}} \right]-1$(phép tính lấy phần nguyên).
$\Rightarrow $ Biên cuối cùng: ${{\Alpha }_{N}}={{\Alpha }_{\circ }}-\Nu .\left( \frac{\Delta \Alpha }{2} \right)$
+) Nếu N lẻ thì AN và A0 trái dấu.
+) Nếu N chẵn thì AN và A0 cùng dấu.
Lấy đối xứng với AN qua x0 hoặc –x0 ta sẽ được vị trí An dừng lại $\in \left[ -{{x}_{\circ }},{{x}_{\circ }} \right].$
Bài tập minh họa
| Bài tập 1: Cho con lắc gồm một lò xo có độ cứng bằng 100 N/m gắn với một vật nhỏ có khối lượng bằng 100 g, dao động trên mặt ngang. Biết hệ số ma sát giữa vật và mặt ngang bằng 0,2 và gia tốc trọng trường là $g=10m/{{s}^{2}},$lấy ${{\pi }^{2}}=10.$Kéo vật lệch khỏi vị trí lò xo không biến dạng 12 cm, dọc theo trục của lò xo, rồi thả nhẹ cho vật dao động. Tính
a) độ giảm biên độ sau mỗi nửa chu kì? b) số lần vật đi qua vị trí lò xo không biến dạng? c) thời gian vật dao động đến khi dừng hẳn lại? d) quãng đường vật đi được kể từ khi bắt đầu dao động đến khi dừng hẳn? e) tốc độ trung bình của vật từ lúc dao động đến khi dừng hẳn? f) tốc độ lớn nhất vật đạt được trong quá trình dao động? |
Lời giải chi tiết:
a) Độ giảm biên độ sau mỗi nửa chu kì = $\frac{\Delta \Alpha }{2}=\frac{2F}{k}=\frac{2\mu mg}{k}=\frac{2.0,2.0,1,1.10}{100}={{4.10}^{-3}}m=0,4cm.$
b) Số dao động thực hiện được đến khi dừng lại: $\Nu =\frac{\Alpha }{\Delta \Alpha }=\frac{12}{2.0,4}=15$dao động.
Số lần vật đi qua vị trí lò xo không biến dạng: ${{n}_{cb}}=2\Nu =2.15=30$lần.
c) Chu kì dao động: $\Tau =2\pi \sqrt{\frac{0,1}{100}}\simeq 0,2s$
Thời gian dao động đến khi dừng lại: $t=\Nu \Tau =15.0,2=3s.$
d) Quãng đường vật đi được đến khi dừng hẳn: $S=\frac{k{{\Alpha }^{2}}}{2F}=\frac{100.0,{{12}^{2}}}{2.0,2.0,1.10}=3,6m.$
e) Tốc độ trung bình của vật từ lúc dao động đến khi dừng hẳn: $v=\frac{S}{t}=\frac{3,6}{3}=1,2m/s.$
f) Tốc độ lớn nhất vật đạt được trong quá trình dao động là tốc độ vật qua vị trí cân bằng lần đầu tiên:
${{v}_{\max 1}}=\omega {\Alpha }’=\omega \left( \Alpha -\frac{\mu mg}{k} \right)=\sqrt{\frac{100}{0,1}}\left( 0,12-\frac{0,2.0,1.10}{100} \right)\approx 3,7m/s.$
