PHƯƠNG PHÁP 2. SỬ DỤNG TRỤC THỜI GIAN
I. LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
1. Lý thuyết

Thời gian vật đi từ VTCB đến li độ x hoặc ngược lại là $t=\frac{1}{\omega }\arcsin \frac{\left| x \right|}{A}$
Thời gian vật đi từ biên đến li độ x hoặc ngược lại thì $t=\frac{1}{\omega }\arccos \frac{\left| x \right|}{A}$
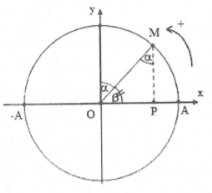
Chứng minh: Khi vật đi từ vị trí x đến vị trí cân bằng, góc vật quét được là $\alpha $
Ta có: $\sin \alpha =\frac{OP}{A}=\left| \frac{x}{A} \right|\Rightarrow \alpha =\arcsin \left| \frac{x}{A} \right|$
Do đó ${{t}_{1}}=\frac{1}{\omega }\arcsin \frac{\left| x \right|}{A}$
Tương tự khi vật đi từ vị trí biên về vị trí có li độ x vật quét được 1 góc là $\beta $
Ta có: $\cos \beta =\left| \frac{x}{A} \right|\Rightarrow \beta =\arccos \left| \frac{x}{A} \right|\Rightarrow t=\frac{1}{\omega }\arccos \left| \frac{x}{A} \right|$
2. Bài tập mẫu
Bài tập mẫu 1: Một vật dao động điều hòa với phương trình $x=8\cos \left( \frac{4\pi t}{3}-\frac{\pi }{2} \right)\left( cm \right)$ . Thời gian ngắn nhất vật đi từ điểm có li độ ${{x}_{1}}=-4\sqrt{3}cm$ đến điểm có li độ ${{x}_{2}}=4cm$ là
Lời giải chi tiết
Thời gian ngắn nhất vật đi từ điểm có li độ ${{x}_{1}}=-4\sqrt{3}cm$ đến điểm có li độ ${{x}_{2}}=4cm$ bằng tổng thời gian ngắn nhất vật đi từ ${{x}_{1}}\Rightarrow $ VTCB và từ VTCB $\Rightarrow {{x}_{2}}$
Do đó ta có: $t={{t}_{1}}+{{t}_{2}}=\frac{1}{\omega }\arcsin \frac{\left| {{x}_{1}} \right|}{A}+\frac{1}{\omega }\arcsin \frac{\left| {{x}_{2}} \right|}{A}$
Hay $t=\frac{1}{\omega }\left( \arcsin \frac{\left| {{x}_{1}} \right|}{A}+\arcsin \frac{\left| {{x}_{2}} \right|}{A} \right)=\frac{3}{4\pi }\left( \arcsin \frac{\sqrt{3}}{2}+\arcsin \frac{1}{2} \right)=0,375s$
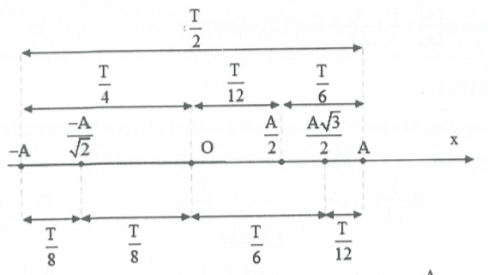
Ghi nhớ các khoảng thời gian đặc biệt:
Vật dao động điều hòa với biên độ A và chu kì T. Khoảng thời gian ngắn nhất vật đi từ:
Vị trí có li độ x = 0 đến x = A hoặc ngược lại là $\Delta t=\frac{T}{4}$
Vị trí có li độ x = 0 đến $x=\pm \frac{A}{2}$ hoặc ngược lại là $\Delta t=\frac{T}{12}$
Vị trí có li độ x = 0 đến $x=\pm \frac{A}{\sqrt{2}}$ hoặc ngược lại là $\Delta t=\frac{T}{8}$
Vị trí có li độ x = 0 đến $x=\pm \frac{A\sqrt{3}}{2}$ hoặc ngược lại là $\Delta t=\frac{T}{6}$
Vị trí có li độ $x=\frac{A}{2}$ đến x = A hoặc ngược lại là $\Delta t=\frac{T}{6}$
Vị trí có li độ $x=\frac{A\sqrt{3}}{2}$ đến x = A hoặc ngược lại là $\Delta t=\frac{T}{12}$
Ta có sơ đồ các khoảng thời gian đặc biệt trong dao động điều hòa:

Từ các phương pháp trên khi làm bài toán về thời gian trong dao động điều hòa ta nên vận dụng một cách linh hoạt các phương pháp đã được học cho mỗi bài toán.
Bài tập mẫu 2: Một vật dao động điều hòa dọc theo trục Ox với phương trình $x=10\cos \left( \frac{4\pi }{3}t-\frac{2\pi }{3} \right)cm$ . Tìm khoảng thời gian ngắn nhất để vật di chuyển trong từng trường hợp sau:
a) Từ vị trí cân bằng đến điểm có li độ x = 5cm
b) Từ vị trí biên dương đến điểm có li độ $x=5\sqrt{3}cm$
c) Từ vị trí có li độ $x=-5\sqrt{2}cm$ đến điểm có li độ x = 5cm
d) Từ điểm có li độ $x=-5cm$ đến điểm có li độ $x=-5\sqrt{3}cm$
e) Từ điểm có li độ $x=5\sqrt{2}cm$ đến điểm có li độ $x=5\sqrt{3}cm$
f) Từ vị trí cân bằng đến vị trí có li độ x = 7cm
g) Từ vị trí biên âm đến vị trí có li độ x = 3cm
h) Từ vị trí có li độ x = 5 cm theo chiều âm đến vị trí có li độ x = -2cm theo chiều dương
Lời giải chi tiết
Ta có: $T=\frac{2\pi }{\omega }=1,5s$
Dựa vào các khoảng thời gian đặt biệt ta có:
a) Thời gian vật đi từ vị trí cân bằng (x = 0) đến điểm có li độ $x=5cm=\frac{A}{2}$ là
$\Delta t=\frac{T}{12}=\frac{1,5}{12}=0,125\left( s \right)$
b) Thời gian vật đi từ vị trí biên dương (x = A) đến điểm có li độ $x=5\sqrt{3}=\frac{A\sqrt{3}}{2}$ là
$\Delta t=\frac{T}{12}=\frac{1,5}{12}=0,125\left( s \right)$
c) Thời gian vật đi từ vị trí có li độ $x=-5\sqrt{2}cm=\frac{-A}{\sqrt{2}}$ đến điểm có li độ $x=5\,cm=\frac{A}{2}$ là
$\Delta t=\frac{T}{8}+\frac{T}{12}=0,3125\left( s \right)$
d) Thời gian vật đi từ điểm có li độ $x=-5cm=\frac{-A}{2}$ đến điểm có li độ $x=-5\sqrt{3}=\frac{-A\sqrt{3}}{2}$ là
$\Delta t=\frac{T}{6}-\frac{T}{12}=\frac{T}{12}=0,125\left( s \right)$
e) Thời gian vật đi từ điểm có li độ $x=5\sqrt{2}=\frac{A}{\sqrt{2}}$ đến điểm có li độ $x=5\sqrt{3}=\frac{A\sqrt{3}}{2}$ là
$\Delta t=\frac{T}{6}-\frac{T}{8}=\frac{T}{24}=0,0625\left( s \right)$
f) Thời gian vật đi từ vị trí cân bằng đến vị trí có li độ x = 7cm là
$\Delta t=\frac{1}{\omega }\arcsin \frac{\left| x \right|}{A}=\frac{3}{4\pi }\arcsin \frac{7}{10}=0,185\left( s \right)$
g) Thời gian vật đi từ vị trí biên âm đến vị trí có li độ x = 3cm là
$\Delta t=\frac{T}{4}+\frac{1}{\omega }\arcsin \frac{\left| x \right|}{A}=\frac{1,5}{4}+\frac{3}{4\pi }\arcsin \frac{3}{10}=0,448\left( s \right)$
h) Thời gian vật đi từ vị trí có li độ x = 5cm theo chiều âm đến vị trí có li độ x = -2cm theo chiều dương là

$\Delta t=\frac{T}{12}+\frac{T}{4}+\frac{1}{\omega }\arccos \left| \frac{x}{A} \right|=\frac{T}{3}+\frac{3}{4\pi }\arccos \left( 0,2 \right)=0,827\left( s \right)$
II. BÀI TẬP ÁP DỤNG PHƯƠNG PHÁP TRỤC THỜI GIAN CÓ LỜI GIẢI CHI TIẾT:
| Bài tập 1: Một vật dao động điều hòa với phương trình $x=8\cos \left( 2\pi t \right)\left( cm \right)$ . Khoảng thời gian ngắn nhất vật đi từ điểm có li độ $x=4\sqrt{2}$ đến vị trí vật có vận tốc là $8\pi \,cm/s$ là
A. $\frac{1}{12}s$ B. $\frac{5}{24}s$ C.$\frac{7}{24}s$ D. $\frac{1}{24}s$ |
Lời giải chi tiết
Khi vật có vận tốc $v=8\pi cm/s=\frac{{{v}_{\max }}}{2}.$ Lại có: ${{\left( \frac{x}{A} \right)}^{2}}+{{\left( \frac{v}{{{v}_{\max }}} \right)}^{2}}=1\Rightarrow x=\frac{\pm A\sqrt{3}}{2}$
Do đó, khi vật có vận tốc là $8\pi cm/s$ thì $\left\{ \begin{array}{} v>0 \\ {} x=\frac{\pm A\sqrt{3}}{2} \\ \end{array} \right.$

Do đó $\Delta {{t}_{\min }}={{t}_{\left( \frac{A\sqrt{2}}{2}\to \frac{A\sqrt{3}}{2} \right)}}=\frac{T}{6}-\frac{T}{8}=\frac{T}{24}=\frac{1}{24}s$ . Chọn D
| Bài tập 2: Một vật dao động điều hoà, biết khoảng thời gian ngắn nhất để vật đi từ điểm có li độ ${{x}_{1}}\,=-A$ đến điểm có li độ ${{x}_{2}}=\frac{A\sqrt{3}}{2}$ là 0,5s. Chu kì dao động của vật là
A. T = 1s B. T = 1,5s C. T = 2s D. T = 1,2s |
Lời giải chi tiết
Ta có: ${{t}_{\left( -A\to \frac{A\sqrt{3}}{2} \right)}}={{t}_{\left( -A\to 0 \right)}}+{{t}_{\left( 0\to \frac{A\sqrt{3}}{2} \right)}}=\frac{T}{4}+\frac{T}{6}=0,5\Rightarrow T=1,2s$ . Chọn D
| Bài tập 3: [Trích đề thi đại học năm 2013]. Một vật nhỏ dao động điều hoà theo phương trình $x=A\cos 4\pi t$ (t tính bằng giây). Tinh từ thời điểm t = 0, khoảng thời gian ngắn nhất để gia tốc của vật bằng một nửa gia tốc cực đại là
A. 0,083s B. 0,104s C. 0,167s D. 0,125s |
Lời giải chi tiết
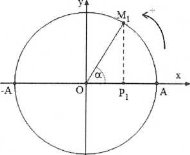
Cách 1: Sử dụng phương pháp đường tròn
Ta có: tại $t=0\Rightarrow x=A,\left| a \right|=\frac{{{a}_{\max }}}{2}\Rightarrow \left| x \right|=\frac{A}{2}$
Tại thời điểm ban đầu $\varphi =0$
Như vậy thời gian ngắn nhất để gia tốc của vật bằng một nửa gia tốc cực đại bằng thời gian vật đi từ x = A đến $x=\frac{A}{2}$
Ta có: $\cos \alpha =\frac{1}{2}\Rightarrow \alpha =\frac{\pi }{3}\Rightarrow {{t}_{\min }}=\frac{\alpha }{\omega }=\frac{1}{12}\left( s \right)$ . Chọn A
Cách 2: Sử dụng trục thời gian
Ta có: tại $t=0\Rightarrow x=A,\left| a \right|=\frac{{{a}_{\max }}}{2}\Rightarrow \left| x \right|=\frac{A}{2};\Delta {{t}_{\min }}={{t}_{\left( A\to \frac{A}{2} \right)}}=\frac{T}{6}=\frac{1}{2}\left( s \right)$ . Chọn A
| Bài tập 4: Một vật dao động điều hoà dọc theo trục Ox với chu kì T và biên độ A = 5 cm . Tính từ lúc vật đang ở biên âm, thời điểm lần thứ 3 vật có tốc độ bằng $\frac{\sqrt{3}}{2}$ lần tốc độ cực đại là t = 1,2s. Tốc độ cực đại của vật là
A. 17,45cm/s B. 15,27cm/s C. 28,36cm/s D. 34,91cm/s |
Lời giải chi tiết
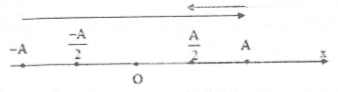
Ta có: $\left| v \right|=\frac{{{v}_{\max }}\sqrt{3}}{2}\Rightarrow \left| x \right|=\frac{A}{2}\Leftrightarrow x=\pm \frac{A}{2}$
Do đó thời điểm lần thứ 3, tính từ biên âm đến khi vật có tốc độ bằng $\frac{\sqrt{3}}{2}$ lần tốc độ cực đại là $\Delta t={{t}_{\left( -A\to A \right)}}+{{t}_{\left( A\to \frac{A}{2} \right)}}=\frac{T}{2}+\frac{T}{6}=\frac{2T}{3}=1,2\Rightarrow T=1,8s$
$\Rightarrow {{v}_{\max }}=\omega A=\frac{2\pi }{T}.A=17,45cm/s$ . Chọn A
| Bài tập 5: Một vật dao động điều hòa với phương trình $x=4\cos \left( 5\pi t-\frac{\pi }{3} \right)\left( cm \right)$. Tính từ thời điểm ban đầu, khoảng thời gian ngắn nhất để vật đến vị trí có gia tốc $a=-50\sqrt{3}{{\pi }^{2}}cm/{{s}^{2}}$ là
A. 0,0167s B. 0,105s C. 0,033s D. 0,33s |
Lời giải chi tiết
Tại thời điểm ban đầu ta có: $\varphi =-\frac{\pi }{3}\Rightarrow \left\{ \begin{array}{} x=2\left( cm \right) \\ {} v>0 \\ \end{array} \right.$
Lại có: $a=-50{{\pi }^{2}}\sqrt{3}=-{{\omega }^{2}}x\Rightarrow x=2\sqrt{3}\left( cm \right)$
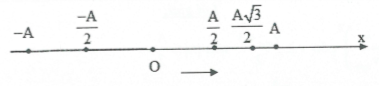
Do đó: $\Delta t={{t}_{\left( \frac{A}{2}\to \frac{A\sqrt{3}}{2} \right)}}={{t}_{\left( 0\to \frac{A\sqrt{3}}{2} \right)}}-{{t}_{\left( 0\to \frac{A}{2} \right)}}=\frac{T}{6}-\frac{T}{12}=\frac{T}{12}=\frac{2\pi }{12\omega }=\frac{1}{30}=0,033\left( s \right)$ . Chọn C
| Bài tập 6: Một vật dao động điều hoà với chu kì T. Nếu chọn gốc thời gian t = 0 lúc vật qua vị trí $x=\frac{A}{2}$ theo chiều dương thì trong nửa chu kì đầu tiên tốc độ của vật cực đại ở thời điểm
A. $t=\frac{T}{8}$ B. $t=\frac{T}{4}$ C. $t=\frac{T}{6}$ D. $t=\frac{5T}{12}$ |
Lời giải chi tiết
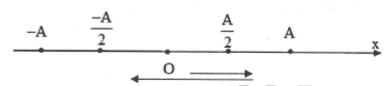
Ta có: $\left| v \right|={{v}_{\max }}\Rightarrow x=0$ . Khi đó $\Delta t={{t}_{\left( \frac{A}{2}\to A \right)}}+{{t}_{\left( A\to 0 \right)}}=\frac{T}{6}+\frac{T}{4}=\frac{5T}{12}$ . Chọn D
| Bài tập 7: Một chất điểm dao động điều hòa với chu kì T. Gọi vmax là tốc độ cực đại của vật trong quá trình dao động, v là tốc độ tức thời của chất điểm. Trong một chu kì, khoảng thời gian mà $v\ge \frac{{{v}_{\max }}}{2}$ là
A. $\frac{2T}{3}$ B.$\frac{T}{3}$ C.$\frac{T}{6}$ D. $\frac{T}{2}$ |
Lời giải chi tiết
Ta có: ${{\left( \frac{x}{A} \right)}^{2}}=1-{{\left( \frac{v}{{{v}_{\max }}} \right)}^{2}},$ do $v\ge \frac{{{v}_{\max }}}{2}$ nên $\left| x \right|\le \frac{A\sqrt{3}}{2}$

Khi đó $\Delta t=2{{t}_{\left( \frac{-A\sqrt{3}}{2}\to \frac{A\sqrt{3}}{2} \right)}}=2.\frac{T}{6}=\frac{T}{3}$ . Chọn B
| Bài tập 8: Một chất điểm dao động điều hòa với chu kì T. Gọi vmax là tốc độ cực đại của vật trong quá trình dao động, v là tốc độ tức thời của chất điểm. Trong một chu kì, khoảng thời gian mà A. 10cm B. 12,5cm C. 13cm D. 15cm |
Lời giải chi tiết
Ta có: ${{\left( \frac{x}{A} \right)}^{2}}=1-{{\left( \frac{v}{{{v}_{\max }}} \right)}^{2}}$ , do $v\ge \frac{{{v}_{\max }}\sqrt{3}}{2}$nên $\left| x \right|\le \frac{A}{2}$
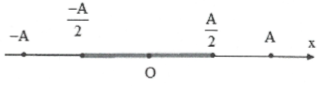
Khi đó $\Delta t=2{{t}_{\left( \frac{-A}{2}\to \frac{A}{2} \right)}}=2.\frac{T}{12}=\frac{T}{6}=0,33\left( s \right)\Rightarrow T=2s\Rightarrow \omega =\frac{2\pi }{T}=\pi \left( rad/s \right)$
Ta có: $x=\frac{a}{-{{\omega }^{2}}}=-10cm\Rightarrow A=\sqrt{{{x}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}}=12,5cm$ . Chọn B
| Bài tập 9: Một vật dao động điều hòa trên quỹ đạo dài 40cm. Tại thời điểm ban đầu vật có li độ là x – 10cm và đang tăng, đến thời điểm $t=\frac{1}{3}s$ thì vật đến vị trí biên lần đầu tiên. Vận tốc của vật tại thời điểm ban đầu là
A. $-20\pi \sqrt{3}cm/s$ B. $20\pi \sqrt{3}cm/s$ C. $-20\pi cm/s$ D. $20\pi cm/s$ |
Lời giải chi tiết
Do $\ell =2A\Rightarrow A=\frac{\ell }{2}=20\left( cm \right).$ Tại $t=0,x=-10$ và đang tăng nên v > 0
Khi đó $t={{t}_{\left( -10\to 20 \right)}}={{t}_{\left( -\,\frac{A}{2}\to A \right)}}={{t}_{\left( -\,\frac{A}{2}\to 0 \right)}}+\,{{t}_{\left( 0\to \frac{A}{2} \right)}}=\frac{T}{12}+\frac{T}{4}=\frac{T}{3}=\frac{1}{3}\Rightarrow T=1\left( s \right)$
Suy ra $v=\omega \sqrt{{{A}^{2}}-{{x}^{2}}}=\frac{2\pi }{T}\sqrt{{{A}^{2}}-{{x}^{2}}}=20\sqrt{3}cm/s$ .Chọn B
| Bài tập 10: Một vật dao động điều hòa với biên độ A, gọi t1 là thời gian ngắn nhất vật đi từ vị trí cân bằng đến điểm có li độ ${{x}_{0}}\left( {{x}_{0}}>0 \right)$ và t2 là thời gian ngắn nhất vật đi từ vị trí có li độ ${{x}_{0}}$ đến biên dương. Biết rằng ${{t}_{2}}=2{{t}_{1}}$ , biên độ dao động của vật là
A. $A={{x}_{0}}\sqrt{3}$ B. $A={{x}_{0}}\sqrt{2}$ C. $A=2{{x}_{0}}$ D. $A=\frac{2{{x}_{0}}}{\sqrt{3}}$ |
Lời giải chi tiết
Ta có: ${{t}_{1}}+{{t}_{2}}=3{{t}_{1}}={{t}_{\left( 0\to A \right)}}=\frac{T}{4}\Rightarrow {{t}_{1}}=\frac{T}{12}={{t}_{\left( 0\to \frac{A}{2} \right)}}\Rightarrow {{x}_{0}}=\frac{A}{2}\Rightarrow A=2{{x}_{0}}$ . Chọn C
| Bài tập 11: Một vật dao động điều hòa với biên độ A, gọi t1 là thời gian ngắn nhất vật đi từ vị trí cân bằng đến điểm có li độ ${{x}_{0}}\left( {{x}_{0}}>0 \right)$ và t2 là thời gian ngắn nhất vật đi từ vị trí có li độ ${{x}_{0}}$ đến biên dương. Biết rằng ${{t}_{2}}=3{{t}_{1}}$ , khi đó:
A. ${{x}_{0}}=\,\frac{A}{3}$ B. ${{x}_{0}}=\,\frac{A}{\sqrt{3}}$ C. ${{x}_{0}}=\frac{A}{2}$ D. ${{x}_{0}}=\,0,383A$ |
Lời giải chi tiết
Ta có: ${{t}_{1}}+{{t}_{2}}=4{{t}_{1}}={{t}_{\left( 0\to A \right)}}=\frac{T}{4}\Rightarrow {{t}_{1}}=\frac{T}{16}={{t}_{\left( 0\to {{x}_{0}} \right)}}=\frac{1}{\omega }\arcsin \frac{{{x}_{0}}}{A}$
Do đó $\frac{T}{16}=\frac{T}{2\pi }\arcsin \frac{{{x}_{0}}}{A}\Rightarrow \sin \frac{\pi }{8}=\frac{{{x}_{0}}}{A}\Rightarrow A=\frac{{{x}_{0}}}{\sin \frac{\pi }{8}}$ . Chọn D
Tổng quát bài toán: Khi ${{t}_{2}}=\,n.{{t}_{1}}$ ta suy ra $A=\frac{{{x}_{0}}}{\sin \frac{\pi }{2\left( n+1 \right)}}\,\,hay\,{{x}_{0}}=A\sin \frac{\pi }{2\left( n+1 \right)}.$
| Bài tập 12: Một vật dao động điều hòa với phương trình $x=A\cos \left( \omega t+\varphi \right)$ . Trong khoảng thời gian 1,75s vật chuyển động từ vị trí có li độ $-\frac{A\sqrt{3}}{2}$ theo chiều dương đến vị trí có li độ $\frac{A}{\sqrt{2}}$ . Khi vật qua vị trí có li độ 3cm thì vật có vận tốc $v=\pi cm/s$ . Gia tốc của vật có độ lớn cực đại là
A. $4,65cm/{{s}^{2}}$ B. $4,65m/{{s}^{2}}$ C. $4,85cm/{{s}^{2}}$ D. $5,48\,m/{{s}^{2}}$ |
Lời giải chi tiết
Ta có: ${{a}_{\max }}={{\omega }^{2}}A$
Mặt khác ${{t}_{\left( -\,\,\frac{A\sqrt{3}}{2}\to \frac{A\sqrt{2}}{2} \right)}}={{t}_{\left( -\,\,\frac{A\sqrt{3}}{2}\to 0 \right)}}+{{t}_{\left( 0\to \frac{A\sqrt{2}}{2} \right)}}=\frac{T}{6}+\frac{T}{8}=1,75\left( s \right)\Rightarrow T=6\left( s \right)$
Do đó $\omega =\frac{2\pi }{T}=\frac{\pi }{3}\left( rad/s \right)$
Lại có: $A=\sqrt{{{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}}=\sqrt{{{3}^{2}}+{{\left( \frac{3}{\pi }.\pi \right)}^{2}}}=3\sqrt{2}cm$
Do vậy ${{a}_{\max }}={{\omega }^{2}}A=\frac{{{\pi }^{2}}}{9}.3\sqrt{2}=4,65cm/{{s}^{2}}$ .Chọn A
| Bài tập 13: Một vật dao động với phương trình $x=6\cos \left( 4\pi t+\frac{\pi }{6} \right)\left( cm \right)$ (t tính bằng s). Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ 3cm theo chiều dương đến vị trí có li độ $-3\sqrt{3}cm$ là
A. $\frac{7}{24}s$ B. $\frac{1}{4}s$ C. $\frac{5}{24}s$ D. $\frac{1}{8}s$ |
Lời giải chi tiết

Ta có thời gian cần tìm là $\Delta t={{t}_{\left( 3\to 6 \right)}}+{{t}_{\left( 6\to 0 \right)}}+{{t}_{\left( 0\to -\,3\sqrt{3} \right)}}=\frac{T}{6}+\frac{T}{4}+\frac{T}{6}=\frac{7T}{12}$
Mặt khác $T=\frac{2\pi }{\omega }=0,5s\Rightarrow \Delta t=\frac{7}{24}s$ . Chọn A
| Bài tập 14: Một chất điểm dao động điều hòa với phương trình $x=20\cos \left( \pi t-\frac{5\pi }{6} \right)cm$ . Tại thời điểm t1 gia tốc của chất điểm cực tiểu. Tại thời điểm ${{t}_{2}}={{t}_{1}}+\Delta t$ (trong đó $\Delta t<2015T$) thì tốc độ của chất điểm là $10\pi \sqrt{2}cm/s$ . Giá trị lớn nhất của $\Delta t$ là
A. 4028,75s B.4028,25s C. 4029,25s D. 4025,75s |
Lời giải chi tiết
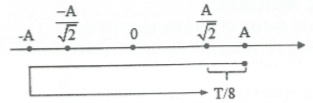
Khi $\left| v \right|=10\sqrt{2}cm/s\Rightarrow x=\pm \sqrt{{{A}^{2}}-\frac{{{v}^{2}}}{{{\omega }^{2}}}}=\pm \frac{A}{\sqrt{2}}$
Tại thời điểm t1 gia tốc của chất điểm cực tiểu (vật ở biên dương)
Vì $\Delta t<2015T$ nên $\Delta {{t}_{\max }}=2015T-\frac{T}{8}=4025,75s$ . Chọn D
| Bài tập 15: Một vật dao động điều hòa mà 3 thời điểm ${{t}_{1}},{{t}_{2}},{{t}_{3}}$ với${{t}_{3}}-{{t}_{1}}=2\left( {{t}_{3}}-{{t}_{2}} \right)$ , vận tốc có cùng độ lớn là ${{v}_{1}}={{v}_{2}}=-{{v}_{3}}=20\sqrt{2}cm/s.$ Vật có vận tốc cực đại là
A. 28,28cm/s B. 40,00cm/s C. 32,66cm/s D. 56,57cm/s |
Lời giải chi tiết
Không mất tính tổng quát có thể xem ở thời điểm ${{t}_{1}}$ vật có vận tốc ${{v}_{0}}$ và đang tăng, đến thời điểm ${{t}_{2}}$ vật có vận tốc ${{v}_{0}}$ và đang giảm, đến thời điểm ${{t}_{3}}$ vật có vận tốc $-{{v}_{0}}$ và đang giảm.
Theo bài ra $\left\{ \begin{array}{} {{t}_{3}}-{{t}_{1}}=2\Delta t+2\left( \frac{T}{4}-\Delta t \right) \\ {} {{t}_{3}}-{{t}_{2}}=2\Delta t \\ \end{array} \right.$
Mà ${{t}_{3}}-{{t}_{1}}=2\left( {{t}_{3}}-{{t}_{2}} \right)$ , suy ra $2\Delta t+2\left( \frac{T}{4}-\Delta t \right)=2.2\Delta t\Rightarrow \Delta t=\frac{T}{8}$
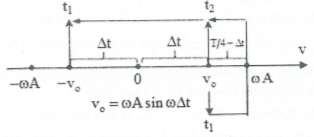
Thay $\Delta t=\frac{T}{8}$ vào công thức ${{v}_{0}}={{v}_{\max }}\sin \frac{2\pi }{T}\Delta t$ ta tính được ${{v}_{\max }}=40cm/s$ . Chọn B.
