VẤN ĐỀ 5: KÍNH THIÊN VĂN
LÝ THUYẾT CHUNG
– Kính thiên văn là dụng cụ quang học bổ trở cho mắt làm tăng góc trông ảnh của những vật ở rất xa (các thiên thể).
– Sơ đồ tạo ảnh: $\text{AB}\xrightarrow{{{\text{L}}_{\text{1}}}}{{\text{A}}_{\text{1}}}{{\text{B}}_{\text{1}}}\xrightarrow{{{\text{L}}_{\text{2}}}}{{\text{A}}_{\text{2}}}{{\text{B}}_{\text{2}}}$
Trong đó ta luôn có: ${{\text{d}}_{1}}=\infty \Rightarrow \text{d}_{\text{1}}^{\text{ }\!\!’\!\!\text{ }}={{\text{f}}_{\text{1}}}$(vì ${{\text{A}}_{\text{1}}}\equiv \text{F}_{\text{1}}^{\text{ }\!\!’\!\!\text{ }}$)
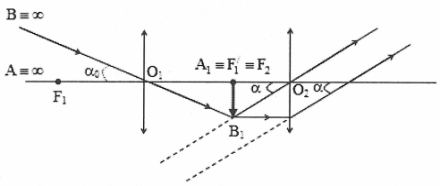
Ngắm chừng ở vô cực
– Độ bội giác: Với kính thiên văn thì $\tan {{\alpha }_{0}}=\frac{{{\text{A}}_{\text{1}}}{{\text{B}}_{\text{1}}}}{{{\text{f}}_{\text{1}}}}$
+) Ngắm chừng ở vô cực: ${{\text{G}}_{\infty }}=\frac{{{\text{f}}_{\text{1}}}}{{{\text{f}}_{\text{2}}}}$
+) Ngắm chừng ở một vị trí bất kì: $\tan \alpha =\frac{{{\text{A}}_{\text{1}}}{{\text{B}}_{\text{1}}}}{{{\text{O}}_{\text{2}}}{{\text{A}}_{\text{1}}}}=\frac{{{\text{A}}_{\text{1}}}{{\text{B}}_{\text{1}}}}{{{\text{d}}_{\text{2}}}}\Rightarrow \text{G}=\frac{{{\text{f}}_{\text{1}}}}{{{\text{f}}_{\text{2}}}}$
+) Khi ngắm chừng ở vô cực thì d2 = f2.
Lưu ý: Khoảng cách giữa vật kính và thị kính của kính thiên văn thay đổi được và được tính theo công thức: $\text{a}={{\text{f}}_{1}}+{{\text{d}}_{2}}\xrightarrow[{{\text{d}}_{2}}={{\text{f}}_{2}}]{\text{ngam }\infty }\text{a}={{\text{f}}_{1}}+{{\text{f}}_{2}}.$
BÀI TẬP VỀ KÍNH THIÊN VĂN
|
Bài tập 1: Vật kính của một kính thiên văn dùng trong nhà trường có tiêu cự f1 = 1 m, thị kính là một thấu kính hội tụ có tiêu cự f2 = 4 cm. Tính khoảng cách giữa hai kính và độ bội giác của kính thiên văn khi ngắm chừng ở vô cực. |
Lời giải chi tiết:
Khi ngắm chừng ở vô cực thì $\text{F}_{1}^{‘}\equiv {{\text{F}}_{2}}$ nên khoảng cách giữa hai kính là:
$\text{a}={{\text{O}}_{1}}{{\text{O}}_{2}}={{\text{f}}_{1}}+{{\text{f}}_{2}}=100+4=104\left( \text{cm} \right)$
Độ bội giác khi ngắm chừng ở vô cực: ${{\text{G}}_{\infty }}=\frac{{{\text{f}}_{1}}}{{{\text{f}}_{2}}}=\frac{100}{4}=25.$
|
Bài tập 2: Vật kính của một kính thiên văn học sinh có tiêu cự f1 = 120 cm, thị kính có tiêu cự f2 = 4 cm. Một học sinh có điểm cực viễn cách mắt 50 cm quan sát ảnh của Mặt Trăng qua kính thiên văn nói trên sao cho mắt không điều tiết. Tính khoảng cách giữa hai kính và độ bội giác. Mắt đặt sát sau thị kính. |
Lời giải chi tiết:
Mắt quan sát ảnh ảo A2B2 ở trạng thái mắt không điều tiết nên A2B2 ở cực viễn của mắt tức
$\text{d}_{2}^{‘}=-{{\text{O}}_{2}}{{\text{A}}_{2}}=-\text{O}{{\text{C}}_{\text{v}}}=-50\text{cm}$
$\Rightarrow $A1B1 cách thị kính: ${{\text{d}}_{2}}={{\text{O}}_{2}}{{\text{A}}_{1}}=\frac{\text{d}_{2}^{‘}{{\text{f}}_{2}}}{\text{d}_{2}^{‘}-{{\text{f}}_{2}}}=\frac{-50.4}{-50-4}\approx 3,7\left( \text{cm} \right)$
Khoảng cách giữa hai kính là: $\text{a}={{\text{f}}_{1}}+{{\text{d}}_{2}}=120+3,7=123,7\left( \text{cm} \right)$
Độ bội giác: ${{\text{G}}_{\text{v}}}=\frac{\alpha }{{{\alpha }_{0}}}\approx \frac{\tan \alpha }{\tan {{\alpha }_{0}}}\text{ }\left( 1 \right)$
Với 
là góc trông ảnh cho bởi $\tan \alpha =\frac{{{\text{A}}_{2}}{{\text{B}}_{2}}}{\left| \text{d}_{2}^{‘} \right|}\text{ }\left( 2 \right)$
${{\alpha }_{0}}$là góc trông Mặt Trăng bằng mắt không qua kính, cho bởi ${{\alpha }_{0}}=\frac{{{\text{A}}_{1}}{{\text{B}}_{1}}}{{{\text{O}}_{1}}{{\text{A}}_{1}}}=\frac{{{\text{A}}_{1}}{{\text{B}}_{1}}}{{{\text{f}}_{1}}}\text{ }\left( 3 \right)$
Từ (1), (2) và (3) ta có: ${{\text{G}}_{\text{v}}}=\frac{{{\text{A}}_{2}}{{\text{B}}_{2}}}{\left| \text{d}_{2}^{‘} \right|}.\frac{{{\text{f}}_{1}}}{{{\text{A}}_{1}}{{\text{B}}_{1}}}\Rightarrow {{\text{G}}_{\text{v}}}=\frac{{{\text{A}}_{2}}{{\text{B}}_{2}}}{{{\text{A}}_{1}}{{\text{B}}_{1}}}.\frac{{{\text{f}}_{1}}}{\left| \text{d}_{2}^{‘} \right|}=\left| \frac{\text{d}_{2}^{‘}}{{{\text{d}}_{2}}} \right|.\frac{{{\text{f}}_{1}}}{\left| \text{d}_{2}^{‘} \right|}=\frac{{{\text{f}}_{1}}}{{{\text{d}}_{2}}}=\frac{120}{3,7}\approx 32,4.$
|
Bài tập 3: Một kính thiên văn khúc xạ được điều chỉnh cho một người có mắt bình thường nhìn được ảnh rõ nét của một vật ở vô cực mà không phải điều tiết. Khi đó khoảng cách giữa vật kính và thị kính là 62 cm và số bội giác của kính là G = 30. a) Xác định tiêu cự của vật kính và thị kính. b) Vật quan sát Mặt Trăng có trông ${{\alpha }_{0}}=\frac{1}{100}\left( \text{rad} \right).$Tính đường kính của Mặt Trăng cho bởi vật kính. |
Lời giải chi tiết:
a) Quá trình tạo ảnh của kính thiên văn giống như quá trình tạo ảnh qua hệ hai thấu kính ghép đồng trục và được tóm tắt qua sơ đồ sau: $\text{AB}\xrightarrow{{{\text{L}}_{\text{1}}}}{{\text{A}}_{\text{1}}}{{\text{B}}_{\text{1}}}\xrightarrow{{{\text{L}}_{\text{2}}}}{{\text{A}}_{\text{2}}}{{\text{B}}_{\text{2}}}$
Vì quan sát Mặt Trăng ở rất xa nên ${{\text{d}}_{1}}=\infty \Rightarrow \text{d}_{1}^{‘}={{\text{f}}_{1}}$
Vì ngắm chừng ở vô cực nên $\text{d}_{2}^{‘}=\infty \Rightarrow {{\text{d}}_{2}}={{\text{f}}_{2}}$
Gọi a là khoảng cách giữa hai kính, ta có: $\text{a}=\text{d}_{1}^{‘}+{{\text{d}}_{2}}={{\text{f}}_{1}}+{{\text{f}}_{2}}=62\text{ }\left( 1 \right)$
Số bội giác của kính thiên văn khi ngắm chừng ở vô cực: ${{\text{G}}_{\infty }}=\frac{{{\text{f}}_{1}}}{{{\text{f}}_{2}}}=30\text{ }\left( 2 \right)$
Từ (1) và (2), suy ra f1 = 60 cm và f2 = 2 cm.
b) Mặt Trăng là vật AB ở xa vô cực $\Rightarrow {{\text{d}}_{1}}=\infty ,$qua vật kính cho ảnh A1B1 ở ngay tiêu điểm ảnh $\text{F}_{1}^{‘}\Rightarrow \text{d}_{1}^{‘}={{\text{f}}_{1}}$
Từ hình vẽ suy ra đường kính của Mặt Trăng cho bởi vật kính là:
$\tan {{\alpha }_{0}}=\frac{{{\text{A}}_{1}}{{\text{B}}_{1}}}{{{\text{f}}_{1}}}\Rightarrow {{\text{A}}_{1}}{{\text{B}}_{1}}={{\text{f}}_{1}}\tan {{\alpha }_{0}}\approx {{\text{f}}_{1}}{{\alpha }_{0}}=\frac{60}{100}=0,6\left( \text{cm} \right)$
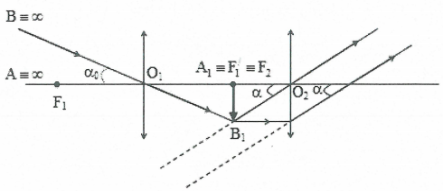
Ngắm chừng ở vô cực
