Dạng 3: Tính quãng đường vật đi được trong khoảng thời gian cho trước
1. PHƯƠNG PHÁP GIẢI
§ Vận tốc trung bình: ${{v}_{tb}}=\frac{\left| {{x}_{2}}-{{x}_{1}} \right|}{{{t}_{2}}-{{t}_{1}}}=\frac{\vartriangle x}{\vartriangle t}$
§ Tốc độ trung bình: $\overline{{{v}_{tb}}}=\frac{S}{\vartriangle t}=\frac{S}{{{t}_{2}}-{{t}_{1}}}$
Trong đó:
+) ${{x}_{1}}$ là tọa độ tại thời điểm ${{t}_{1}}.$
+) ${{x}_{2}}$ là tọa độ tại thời điểm ${{t}_{2}}.$
+) S là quãng đường vật đi được trong khoảng thời gian từ ${{t}_{1}}$ tới ${{t}_{2}}.$
2. BÀI TẬP MINH HỌA DẠNG 3
| Bài tập 1: [Trích đề thi đại học năm 2009]. Một vật dao động điều hòa có độ lớn vận tốc cực đại là 31,4 cm/s. Lấy $\pi =3,14.$ Tốc độ trung bình của vật trong một chu kì dao động là
A. 20 cm/s. B. 10 cm/s. C. 0. D. 15 cm/s. |
Lời giải chi tiết
Tốc độ trung bình của vật là $\overline{{{v}_{tb}}}=\frac{S}{\vartriangle t}=\frac{S}{{{t}_{2}}-{{t}_{1}}}=\frac{4A}{T}=\frac{2\omega A}{\pi }=\frac{2{{v}_{\max }}}{\pi }=20cm/s.$ Chọn A.
| Bài tập 2: Một chất điểm dao động điều hòa theo một quỹ đạo thẳng dài 14 cm với chu kì 1 s. Tốc độ trung bình của chất điểm từ thời điểm ${{t}_{0}}$ chất điểm qua vị trí có li độ 3,5 cm theo chiều dương đến thời điểm gia tốc của chất điểm có độ lớn cực đại lần thứ 3 (kể từ ${{t}_{0}}$) là
A. 27,3 cm/s. B. 28,0 cm/s. C. 27,0 cm/s. D. 26,7 cm/s. |
Lời giải chi tiết
Biên độ dao động của vật là $A=\frac{\ell }{2}=7cm.$
Gia tốc có độ lớn cực đại khi vật ở vị trí biên.
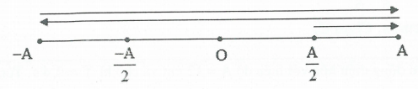
Quãng đường vật đi được là $S=\frac{A}{2}+4A=31,5cm.$
Thời gian vật đi là $\vartriangle t={{t}_{\left( \frac{A}{2}\to A \right)}}+T=\frac{T}{6}+T=\frac{7T}{6}=\frac{7}{6}.$
Tốc độ trung bình của vật là $\overline{{{v}_{tb}}}=\frac{S}{\vartriangle t}=27cm/s.$ Chọn C.
| Bài tập 3: Một chất điểm dao động điều hòa trên trục Ox có vận tốc bằng 0 tại 2 thời điểm liên tiếp ${{t}_{1}}=1,75s$ và ${{t}_{2}}=2,55s$, tốc độ trung bình trong khoảng thời gian đó là 16 cm/s. Tọa độ chất điểm tại thời điểm t = 0 là
A. 0 cm. B. -8 cm. C. -4 cm. D. -3 cm. |
Lời giải chi tiết
Vận tốc của vật bằng 0 ở hai biên ta có: $\frac{T}{2}={{t}_{2}}-{{t}_{1}}=0,75\Rightarrow T=1,5s.$
Mặt khác $\overline{{{v}_{tb}}}=\frac{S}{\vartriangle t}=16cm/s\Leftrightarrow \frac{2A}{0,75}=16\Rightarrow A=6cm.$
Lại có: ${{t}_{1}}=T+\frac{T}{6}$. Giả sử tại thời điểm ${{t}_{1}}$ vật ở biên dương

Khi đó thời điểm ban đầu vật ở li độ ${{x}_{0}}=\frac{A}{2}$, nếu vật ở ${{t}_{1}}$ vật ở biên âm thì ${{x}_{0}}=-\frac{A}{2}$.
Suy ra ${{x}_{o}}=-3$ hoặc ${{x}_{o}}=3$. Chọn D.
| Bài tập 4: Một chất điểm dao động điều hòa trên trục Ox. Tốc độ trung bình của chất điểm tương ứng với khoảng thời gian thế năng không vượt quá 3 lần động năng trong 1 nửa chu kỳ là $300\sqrt{3}cm/s$. Tốc độ cực đại của dao động là
A. 400 cm/s. B. 200 cm/s. C. $2\pi $m/s. D. $4\pi $m/s. |
Lời giải chi tiết
Ta có vị trí: ${{\text{W}}_{t}}=3{{\text{W}}_{d}}\Rightarrow x=\pm \frac{A\sqrt{3}}{2}.$
Tốc độ trung bình tương ứng với khoảng thời gian thế năng không vượt quá ba lần động năng trong một nửa chu kỳ là $\overline{v}=\frac{2.\frac{A\sqrt{3}}{2}}{\frac{T}{6}+\frac{T}{6}}=\frac{3\sqrt{3}\omega A}{2\pi }=\frac{3\sqrt{3}{{v}_{\max }}}{2\pi }=300\sqrt{3}.$
Do đó: ${{v}_{\max }}=200\pi cm/s.$ Chọn C.
| Bài tập 5: Một vật dao động điều hòa với biên độ A = 12 cm và chu kì T = 0,4s. Tốc độ trung bình lớn nhất của vật trong khoảng thời gian $\vartriangle t=\frac{1}{15}s$ là
A. 1,8 m/s. B. 1,5 m/s. C. 2,1 m/s. D. 1,2 m/s. |
Lời giải chi tiết
Tốc độ lớn nhất khi quãng đường vật đi được trong thời gian trên là lớn nhất.
Ta có: $\vartriangle t=\frac{1}{15}s=\frac{T}{6}=2.\frac{T}{12}\Rightarrow {{S}_{\max }}=2.\frac{A}{2}=A=12cm.$
Do đó: $\overline{{{v}_{\max }}}=\frac{12}{{1}/{15}\;}=180cm/s.$ Chọn A.
| Bài tập 6: Một chất điểm dao động điều hòa trên trục Ox có vận tốc bằng 0 tại hai thời điểm liên tiếp ${{t}_{1}}=1,625s$ và ${{t}_{2}}=2,375s$ tốc độ trung bình trong khoảng thời gian đó là 16 cm/s. Ở thời điểm t = 0, vận tốc ${{v}_{0}}cm/s$ li độ ${{x}_{0}}$cm của vật thỏa mãn hệ thức:
A. ${{x}_{0}}{{v}_{0}}=12\pi \sqrt{3}.$ B. ${{x}_{0}}{{v}_{0}}=-12\pi \sqrt{3}.$ C. ${{x}_{0}}{{v}_{0}}=4\pi \sqrt{3}.$ D. ${{x}_{0}}{{v}_{0}}=-4\pi \sqrt{3}.$ |
Lời giải chi tiết
Ta có: Vận tốc của vật bằng 0 tại biên. Khi đó $\frac{T}{2}={{t}_{2}}-{{t}_{1}}=0,75\Rightarrow T=1,5s.$
Tốc độ trung bình của vật trong khoảng thời gian đó là $\overline{v}=\frac{S}{\frac{T}{2}}=\frac{2A}{0,75}=16\Rightarrow A=6cm.$
Mặt khác ${{t}_{1}}=T+\frac{T}{12}$ do đó nếu vật ở biên âm thì $\left[ \begin{array}{} {{x}_{0}}=\frac{-A\sqrt{3}}{2} \\ {} {{v}_{0}}=\frac{-{{v}_{\max }}}{2} \\ \end{array} \right.$
Nếu thời điểm ${{t}_{1}}$ vật ở biên dương thì $\left[ \begin{array}{} {{x}_{0}}=\frac{A\sqrt{3}}{2} \\ {} {{v}_{0}}=\frac{{{v}_{\max }}}{2} \\ \end{array} \right.$
Do đó ${{x}_{0}}{{v}_{0}}=\frac{{{v}_{\max }}A\sqrt{3}}{4}=\frac{\omega {{A}^{2}}\sqrt{3}}{4}=\frac{2\pi }{T}.\frac{{{A}^{2}}\sqrt{3}}{4}=12\pi \sqrt{3}.$ Chọn A.
| Bài tập 7: [Trích đề thi đại học năm 2010]. Một chất điểm dao động điều hòa với chu kì T. Trong khoảng thời gian ngắn nhất khi đi từ vị trí biên có li độ x = A đến vị trí $x=\frac{-A}{2}$, chất điểm có tốc độ trung bình là A. $\frac{3A}{2T}.$ B. $\frac{6A}{T}.$ C. $\frac{4A}{T}.$ D. $\frac{9A}{2T}.$ |
Lời giải chi tiết
Thời gian ngắn nhất vật đi từ vị trí biên có li độ x = A đến vị trí $x=\frac{-A}{2}$là
$\vartriangle t={{t}_{\left( A\to 0\to \frac{A}{2} \right)}}=\frac{T}{4}+\frac{T}{12}=\frac{T}{3}.$
Quãng đường vật đi được là $S=\frac{3A}{2}\Rightarrow \overline{v}=\frac{S}{\vartriangle t}=\frac{\frac{3A}{2}}{\frac{T}{3}}=\frac{9A}{2T}.$ Chọn D.
| Bài tập 8: [Trích đề thi đại học năm 2012]. Một chất điểm dao động điều hòa với chu kì T. Gọi ${{v}_{TB}}$ là tốc độ trung bình của chất điểm trong một chu kì, v là tốc độ tức thời của chất điểm. Trong một chu kì, khoảng thời gian mà $v\ge \frac{\pi }{4}{{v}_{TB}}$ là
A. $\frac{2T}{3}.$ B. $\frac{T}{3}.$ C. $\frac{T}{6}.$ D. $\frac{T}{2}.$ |
Lời giải chi tiết
Ta có: ${{v}_{TB}}=\frac{4A}{T}=\frac{4A}{\frac{2\pi }{\omega }}=\frac{2{{v}_{\max }}}{\pi }\Rightarrow v\ge \frac{\pi }{4}{{v}_{TB}}\Leftrightarrow v\ge \frac{{{v}_{\max }}}{2}.$
Lại có: ${{\left( \frac{x}{2} \right)}^{2}}+{{\left( \frac{v}{{{v}_{\max }}} \right)}^{2}}=1\Rightarrow v\ge \frac{{{v}_{\max }}}{2}\Leftrightarrow \left| x \right|\le \frac{\sqrt{3}}{2}A$
Do đó $\vartriangle t=4.{{t}_{\left( 0\to \frac{A\sqrt{3}}{2} \right)}}=4\frac{T}{6}=\frac{2T}{3}.$ Chọn A.
| Bài tập 9: [Trích đề thi thử chuyên Vĩnh Phúc 2017]. Một con lắc lò xo có chiều dài tự nhiên ${{\ell }_{o}}=30cm$ treo thẳng đứng, đầu dưới của lò xo treo một vật có khối lượng m. Từ vị trí cân bằng O của vật kéo vật thẳng đứng xuống dưới 10 cm rồi thả nhẹ không vận tốc ban đầu. Gọi B là vị trí thả vật, M là trung điểm của OB thì tốc độ trung bình khi vật đi từ O đến M và tốc độ trung bình khi vật đi từ M đến B có hiệu bằng 50 cm/s. Lấy $g=10m/{{s}^{2}}$. Khi lò xo có chiều dài 34 cm thì tốc độ của vật có giá trị xấp xỉ bằng
A. 42 cm/s. B. 0. C. 105 cm/s. D. 91 cm/s. |
Lời giải chi tiết
Tốc độ trung bình trên đoạn đường BM là ${{v}_{BM}}=\frac{\frac{A}{2}}{\frac{T}{6}}=\frac{3A}{T}.$
Tốc độ trung bình trên đoạn đường OM là ${{v}_{OM}}=\frac{\frac{A}{2}}{\frac{T}{12}}=\frac{6A}{T}.$
${{v}_{OM}}-{{v}_{BM}}=\frac{3A}{T}=50\Rightarrow T=\frac{3}{5}\Rightarrow \omega =\frac{10\pi }{3}\Rightarrow \vartriangle {{\ell }_{0}}=\frac{g}{{{\omega }^{2}}}=9cm.$
Khi lò xo dài 34 cm suy ra $x=-5cm=\frac{-A}{2}\Rightarrow \left| v \right|=\frac{\omega A\sqrt{3}}{2}=90,69cm/s.$ Chọn D.
| Bài tập 10: Một vật dao động với biên độ 10 cm, trong một chu kì dao động thời gian vật có tốc độ lớn hơn một giá trị ${{v}_{0}}$ là 1s. Tốc độ trung bình khi đi một chiều giữa 2 vị trí có tốc độ ${{v}_{0}}$ là 24 cm/s. Tính ${{v}_{0}}$.
A. 20,59 cm/s. B. 50,94 cm/s. C. 18,14 cm/s. D. 20,94 cm/s. |
Lời giải chi tiết
Giả sử khi vật có vận tốc ${{v}_{0}}$ thì li độ là ${{x}_{0}}$.
Khi đó: thời gian vật có tốc độ lớn hơn một giá trị ${{v}_{0}}$ bằng thời gian vật có li độ nhỏ hơn ${{x}_{0}}$.
Ta có: $\vartriangle t=4\frac{1}{\omega }\arcsin \frac{\left| {{x}_{o}} \right|}{10}=1\left( 1 \right).$ Lại có: $24=\frac{2{{x}_{0}}}{0,5}\Rightarrow {{x}_{0}}=6\left( cm \right).$
Do đó $\frac{4}{\omega }\arcsin \frac{6}{10}=1\Rightarrow \omega =2,574\Rightarrow {{v}_{0}}=\omega \sqrt{{{A}^{2}}-{{x}^{2}}}=20,59cm/s.$ Chọn D.
| Bài tập 11: Một chất điểm dao động điều hòa trên trục Ox, gia tốc của vật có độ lớn cực đại tại 2 thời điểm liên tiếp là ${{t}_{1}}=0,1875s$ và ${{t}_{2}}=0,3125s$. Vận tốc trung bình trong khoảng thời gian đó là -160 cm/s. Phương trình li độ của vật là
A. $x=10\cos \left( 8\pi t+\frac{\pi }{2} \right)cm.$ B. $x=5\cos \left( 4\pi t+\frac{\pi }{2} \right)cm.$ C. $x=10\cos 4\pi tcm.$ D. $x=10\cos \left( 8\pi t-\frac{\pi }{2} \right)cm.$ |
Lời giải chi tiết
2 vị trí độ lớn $a{{ {} }_{\max }}$ ở tại 2 biên: ${T}/{2}\;=0,3125-0,1875=0,125\Rightarrow T=0,25s\Rightarrow \omega =8\pi rad/s$
Vận tốc trung bình: ${{v}_{tb}}=\frac{{{x}_{2}}-{{x}_{1}}}{\vartriangle t}=-160<0\Rightarrow {{x}_{2}}=-A;{{x}_{1}}=A$ và $\frac{-A-A}{0,125}=-160 {} \Rightarrow A=10cm$
Do ${{t}_{1}}=0,1875s={3T}/{4}\;$ ở tại biên dương $\Rightarrow $ vị trí tại thời điểm ban đầu: ${{x}_{o}}=0$ theo chiều âm
$\Rightarrow \varphi ={\pi }/{2}\;\Rightarrow x=10\cos \left( 8\pi t+{\pi }/{2}\; \right)cm.$ Chọn A.
| Bài tập 12: Một vật dao động điều hòa với biên độ A, vào thời điểm t = 0, vật qua VTCB theo chiều dương. Đến thời điểm t = 43s vật qua vị trí có li độ $\frac{A\sqrt{3}}{2}$ lần thứ 30. Tốc độ trung bình trong khoảng thời gian đó là 6,203 cm/s. Tính gia tốc cực đại.
A. $44,6cm/{{s}^{2}}$ B. $34,6cm/{{s}^{2}}$ C. $24,6cm/{{s}^{2}}$ D. $20,5cm/{{s}^{2}}$ |
Lời giải chi tiết
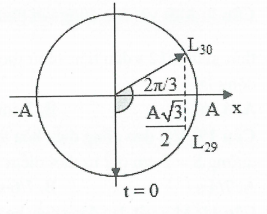
| Một chu kỳ vật qua vị trí $\frac{A\sqrt{3}}{2}$ 2 lần
Ta có: 30 lần = 14.2 lần + 2 lần $\Leftrightarrow 43s=14T+\vartriangle t$ Thời gian $\vartriangle t$ tương ứng với góc ${2\pi }/{3}\;$ như trong hình $\Rightarrow \vartriangle t={T}/{3}\;$ $\Rightarrow 43s=14T+\frac{T}{3}\Rightarrow T=3s\Rightarrow \omega =\frac{2\pi }{3}{rad}/{s}\;$ Quãng đường vật đi được trong thời gian 43 s đó là: $\begin{array}{} S=14.4A+A+(A-\frac{A\sqrt{3}}{2})=58A-\frac{A\sqrt{3}}{2}=\overline{v}.t \\ {} \Leftrightarrow 58A-\frac{A\sqrt{3}}{2}=6,203.43\Rightarrow A=4,67cm \\ {} \Rightarrow {{a}_{\max }}=A{{\omega }^{2}}=4,67.{{\left( \frac{2\pi }{3}\right)}^{2}}=20,5cm/{{s}^{2}}. \\ \end{array}$ Chọn D. |
 |
