I. Lý thuyết con lắc đơn
– Khái niệm: Con lắc đơn gồm một vật nhỏ, khối lượng m, treo ở đầu của một sợi dây không dãn khối lượng không đáng kể, chiều dài l.
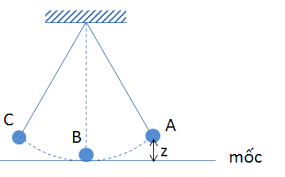
– Phương trình dao động điều hòa của con lắc đơn:
\(s = {s_0}\cos \left( {\omega t + \varphi } \right)\) hay \(\alpha = {\alpha _0}\cos \left( {\omega t + \varphi } \right)\) với \({s_0} = l{\alpha _0}\)
– Các đại lượng trong dao động điều hòa của con lắc đơn:
+ Tần số góc, chu kì, tần số:
\(\omega = \sqrt {\dfrac{g}{l}} ,T = 2\pi \sqrt {\dfrac{l}{g}} ,f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{g}{l}} \)
– Hệ thức độc lập:
\(s_0^2 = {s^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\) hay \(\alpha _0^2 = {\alpha ^2} + \dfrac{{{v^2}}}{{{l^2}{\omega ^2}}}\) hoặc \(\alpha _0^2 = {\alpha ^2} + \dfrac{{{v^2}}}{{\lg }}\)
II. Vận tốc – Lực của con lắc đơn
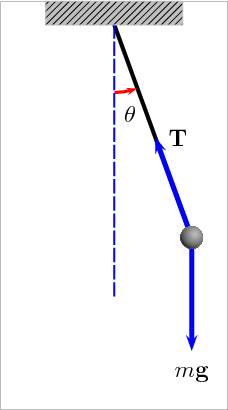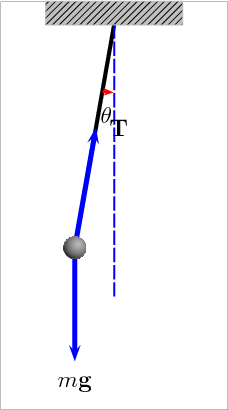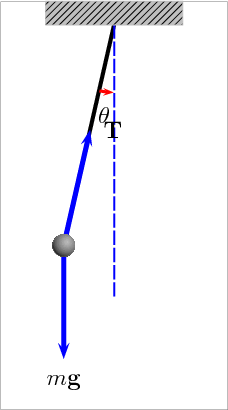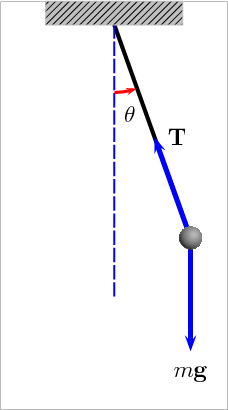
– Vận tốc vật ở li độ góc \(\alpha \) bất kì:
\({v_\alpha } = \pm \sqrt {2gl\left( {\cos \alpha – \cos {\alpha _0}} \right)} \)
Đặc biệt:
+ Nếu \({\alpha _0} \le {10^0}\) thì có thể tính gần đúng: \({v_\alpha } = \pm \sqrt {gl\left( {\alpha _0^2 – {\alpha ^2}} \right)} \)
+ Khi vật qua vị trí cân bằng:
\({v_{\max }} = \sqrt {2gl\left( {1 – \cos {\alpha _0}} \right)} \)
+ Khi \({\alpha _0} \le {10^0}\) thì \({v_{\max }} = {\alpha _0}\sqrt {gl} = \omega {S_0}\)
– Lực căng dây ở li độ góc \(\alpha \) bất kì:
\(T = mg\left( {3\cos \alpha – 2\cos {\alpha _0}} \right)\)
+ Khi qua vị trí cân bằng:
\(\alpha = 0 \to \cos \alpha = 1 \to {T_{\max }} = mg\left( {3 – 2\cos {\alpha _0}} \right)\)
+ Khi đến vị trí biên: \(\alpha = \pm {\alpha _0} \to \cos \alpha = \cos {\alpha _0} \to {T_{\min }} = mg\cos {\alpha _0}\)
III. Năng lượng của con lắc đơn
– Động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\)
– Thế năng: \({{\rm{W}}_t} = mgl\left( {1 – \cos \alpha } \right)\)
– Cơ năng:
\({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = mgl\left( {1 – \cos {\alpha _0}} \right)\)
