I. Lý thuyết dao động điều hòa
– Định nghĩa: Dao động điều hòa là dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian.
– Phương trình dao động điều hòa: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Trong đó:
+ x: li độ của dao động
+ A: biên độ dao động
+ \(\omega \): tần số góc của dao động (đơn vị rad/s)
+ \(\omega t + \varphi \): pha của dao động tại thời điểm t
+ \(\varphi \): pha ban đầu của dao động
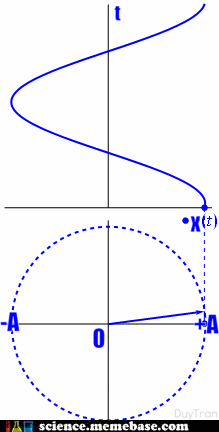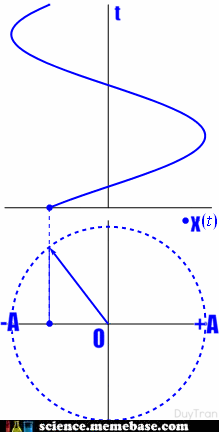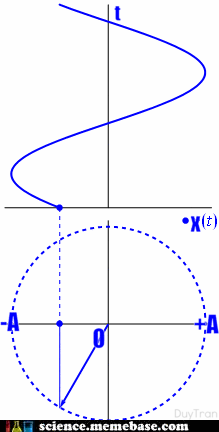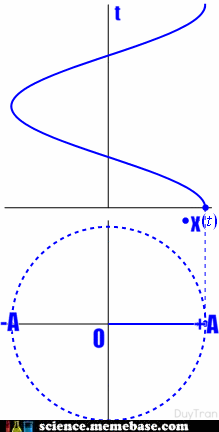
– Phương trình vận tốc: \(v = x’ = \omega A\cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\)
+ Tại VTCB vận tốc có độ lớ cực đại \({v_{\max }} = \omega A\)
+ Tại biên vận tốc bằng 0
+ Vận tốc nhanh pha hơn li độ một góc \(\frac{\pi }{2}\) và vận tốc đổi chiều tại biên độ.
– Phương trình gia tốc: \(a = v’ = {\omega ^2}A\cos \left( {\omega t + \varphi + \pi } \right)\)
+ Vectơ gia tóc luôn luôn hướng về vị trí cân bằng
+ Tại biên gia tốc có độ lớn cực đại \({a_{\max }} = {\omega ^2}A\), tại VTCB gia tốc bằng 0
+ Gia tốc nhanh pha hơn vận tốc một góc \(\frac{\pi }{2}\) và ngược pha với li độ.
II. Các đại lượng đặc trưng của dao động điều hòa
– Chu kì T (s): là khoảng thời gian để vật thực hiện được một dao động toàn phần:
\(T = \dfrac{{2\pi }}{\omega } = \dfrac{{\Delta t}}{N}\) với N là tổng số dao động trong thời gian \(\Delta t\)
– Tần số f (Hz): là số dao động toàn phần thực hiện được trong 1 giây
\(f = \dfrac{\omega }{{2\pi }} = \dfrac{1}{T}\)
– Tần số góc \(\omega \) (rad/s): là đại lượng liên hệ với chu kì T hay tần số f bằng hệ thức:
\(\omega = \frac{{2\pi }}{T} = 2\pi f\)
– Biên độ dao động A: là độ lệch lớn nhất của vật dao động so với vị trí cân bằng của nó.
\({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = \dfrac{{{a^2}}}{{{\omega ^4}}} + \dfrac{{{v^2}}}{{{\omega ^2}}}\)
\(A = \dfrac{{{v_{\max }}}}{\omega } = \dfrac{{{a_{\max }}}}{{{\omega ^2}}} = \dfrac{L}{2} = \dfrac{S}{4} = \dfrac{{v_{\max }^2}}{{{a_{\max }}}}\)
Trong đó:
+ L là chiều dài quỹ đạo chuyển động của vật: L = 2A
+ S là quãng đường vật đi được trong một chu kì: S = 4A
III. Dạng 1: Viết phương trình dao động điều hòa
Phương trình dao động tổng quát: \(x{\rm{ }} = {\rm{ }}Acos\left( {\omega t{\rm{ }} + {\rm{ }}\varphi } \right)\)
– Bước 1: Tìm A:
$\left\{ \begin{array}{l}
A = \dfrac{{{v_{{\rm{max}}}}}}{\omega } = \dfrac{{{a_{{\rm{max}}}}}}{{{\omega ^2}}} = \dfrac{L}{2} = \dfrac{S}{4} = \dfrac{{{v_{{\rm{max}}}}^2}}{{{a_{{\rm{max}}}}}}\\
{A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {\dfrac{a}{{{\omega ^4}}}^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}
\end{array} \right.$
- L: chiều dài quỹ đạo của dao động
- S: quãng đường vật đi được trong một chu kì
– Bước 2: Tìm \(\omega\):
\(\omega = \sqrt {\dfrac{k}{m}} = 2\pi f = \dfrac{{2\pi }}{T} = \sqrt {\dfrac{{{a_{{\rm{max}}}}}}{A}} = \dfrac{{{v_{{\rm{max}}}}}}{A} = \dfrac{{{a_{{\rm{max}}}}}}{{{v_{{\rm{max}}}}}} = \sqrt {\dfrac{{{v^2}}}{{{A^2} – {x^2}}}} \)
Trong đó:
- Chu kì T: \(T = \dfrac{t}{N}\)
- Tần số f: \(f = \dfrac{N}{t}\)
- N là số dao động vật thực hiện được trong khoảng thời gian t
– Bước 3: Tìm \(\varphi \)
Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi \\{\rm{v = – A}}\omega {\rm{sin}}\varphi \end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\dfrac{{{x_0}}}{A}\\\sin \varphi = – \dfrac{v}{{A\omega }}\end{array} \right. \to \varphi = ?\)
– Nếu \(v > 0 \to \sin \varphi < 0\) vật chuyển động theo chiều dương
– Nếu \(v < 0 \to \sin \varphi > 0\) vật chuyển động theo chiều âm
Ta có thể thay đổi thứ tự các bước tùy theo tính chất đề bài.
IV. Dạng 2: Cho phương trình vận tốc hoặc gia tốc, tìm phương trình li độ x
Giả sử phương trình của v và a là:
\(\left\{ \begin{array}{l}v = \omega Ac{\rm{os(}}\omega {\rm{t + }}{\varphi _v})\\a = \omega {\rm{Acos(}}\omega {\rm{t + }}{\varphi _a})\end{array} \right.\)
– Bước 1: Tìm A, ω: từ phương trình của v hoặc a.
– Bước 2: Tìm \({\varphi _x}:\left\{ \begin{array}{l}{\varphi _x} = {\varphi _v} – \frac{\pi }{2}\\{\varphi _x} = {\varphi _a} – \pi \end{array} \right.\)
(do vận tốc nhanh pha hơn x một góc \(\pi /2\) và gia tốc a ngược pha với x)
