I. Biểu diễn dao động điều hòa bằng vectơ quay
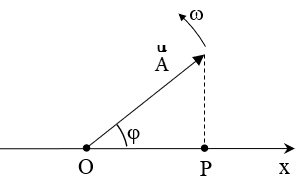
– Mỗi dao động điều hòa được biểu diễn bằng một vectơ quay ngược chiều kim đồng hồ quanh gốc O, có đặc điểm:
+ Gốc tại gốc tọa độ của trục Ox
+ Có độ dài bằng biên độ dao động A
+ Hợp với trục Ox một góc bằng pha ban đầu
– Khi đó, hình chiếu P của ngọn vecto xuống trục Ox biểu diễn một dao động điều hòa:
– Tổng hợp hai dao động điều hòa cùng phương cùng tần số – Phương pháp giản đồ Fre-nen:
Lần lượt vẽ hai véctơ quay biểu diễn hai phương trình dao động thành phần. Sau đó vẽ véctơ tổng của hai véctơ trên. Véctơ tổng la véctơ quay biểu diễn phương trình của dao động tổng hợp.
II. Các đại lượng đặc trưng của dao động tổng hợp
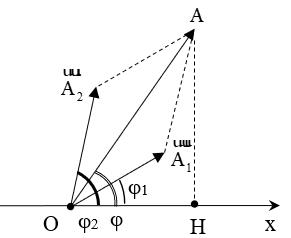
– Biên độ và pha ban đầu của dao động tổng hợp:
\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}{\rm{cos(}}{\varphi _2} – {\varphi _1})\\tan\varphi = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}{\rm{cos}}{\varphi _1} + {A_2}{\rm{cos}}{\varphi _2}}}\end{array}\)
Trường hợp độ lệch pha của hai dao động đặc biệt:
+ \(\Delta \varphi = {\varphi _2} – {\varphi _1} = k2\pi \): hai dao động cùng pha
\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2} = {({A_1} + {A_2})^2}\\ \to A = {A_1} + {A_2}\end{array}\)
+ \(\Delta \varphi = {\varphi _2} – {\varphi _1} = (2k + 1)\pi \): hai dao động ngược pha
\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 – 2{A_1}{A_2} = {({A_1} – {A_2})^2}\\ \to A = \left| {{A_1} – {A_2}} \right|\end{array}\)
+ \(\Delta \varphi = {\varphi _2} – {\varphi _1} = \dfrac{{2k + 1}}{2}\pi \) : hai dao động vuông pha
\({A^2} = A_1^2 + A_2^2\)
