DẠNG 2. BIÊN ĐỘ MỚI CỦA CON LẮC SAU BIẾN CỐ
I. LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
Xét một con lắc lò xo, vị trí cân bằng là vị trí có tổng hợp lực bằng không:
$\overrightarrow{{{F}_{h\ell }}}=\vec{0}\Rightarrow \overrightarrow{{{F}_{dh}}}+\overrightarrow{{{F}_{khac}}}=\vec{0}\Rightarrow {{F}_{dh}}={{F}_{khac}}\Rightarrow k.\Delta {{\ell }_{o}}={{F}_{khac}}=\Delta {{\ell }_{o}}=\frac{{{F}_{khac}}}{k}$
Với$\overrightarrow{{{F}_{khac}}}$là tổng các lực tác dụng lên vật nặng trừ lực đàn hồi $\overrightarrow{{{F}_{dh}}}$.
Để thay đổi vị trí cân bằng người ta có thể thêm hoặc bớt lực $\overrightarrow{{{F}_{t}}}$ tác dụng vào vật:
$\overrightarrow{{{F}_{h\ell }}}=\vec{0}\Rightarrow \overrightarrow{{{F}_{dh}}^{\prime }}+\overrightarrow{{{F}_{khac}}}+\overrightarrow{{{F}_{t}}}=\vec{0}$
Đặt $\overrightarrow{{{F}_{khac}}}+\overrightarrow{{{F}_{t}}}=\overrightarrow{{{{{F}’}}_{khac}}}\Rightarrow {{{F}’}_{dh}}={{{F}’}_{khac}}\Rightarrow k.\Delta {{\ell }_{o}}^{\prime }={{{F}’}_{khac}}\Rightarrow \Delta {{\ell }_{o}}^{\prime }=\frac{{{{{F}’}}_{khac}}}{k}$
$\Rightarrow \Delta {{\ell }_{o}}\ne \Delta {{\ell }_{o}}^{\prime }$: VTCB của CLLX đã thay đổi
Như vậy. khi thêm hay bớt lực $\overrightarrow{{{F}_{t}}}$ thì vị trí cân bằng thay đổi dịch chuyển theo hướng của lực $\overrightarrow{{{F}_{t}}}$ đến vị trí mới cách vị trí cân bằng cũ một đoạn: $\frac{{{F}_{t}}}{k}$
CLLX dao động quanh vị trí cân bằng của nó. Nếu vị trí cân bằng của nó thay đổi thì tính chất dao động của nó thay đổi.
Hướng làm giải quyết bài toán có vị trí cân bằng thay đổi: Xác định thời điểm thay đổi vtcb (thời điểm thêm hoặc bớt lực). Xét thời điểm ngay trước và ngay sau khi thay đổi vtcb:
|
|
Ngay trước |
Ngay sau |
|
VTCB |
O |
O’ |
|
Vận tốc |
v |
v’=v |
|
Li độ |
x (so với gốc O) |
${x}’=x\pm O{O}’$(so với gốc O’) Với $O{O}’=\frac{{{F}_{t}}}{k}$ |
|
Tần số góc |
$\omega $ |
${\omega }’$(tùy xem m, k có thay đổi không) |
|
Biên độ |
|
${A}’=\sqrt{{{\left( \frac{{{v}’}}{{{\omega }’}} \right)}^{2}}+{{{{x}’}}^{2}}}$ |
Chú ý:
+) Khi con lắc lò xo dao động điều hòa được đặt thêm hoặc lấy bớt gia trọng $\Delta m$ sẽ chịu thêm hoặc bớt đi tác dụng của trọng lực $\pm \overrightarrow{{{P}_{\Delta m}}}=\pm \Delta m.\vec{g}$.
+) Khi con lắc dao động điều hòa tích điện đặt trong điện trường sẽ chịu thêm tác dụng của lực điện:
$\overrightarrow{{{F}_{d}}}=q.\overrightarrow{E}\left\{ \begin{array}{} q>0\Rightarrow \overrightarrow{{{F}_{d}}}\uparrow \uparrow \overrightarrow{E} \\ {} q<0\Rightarrow \overrightarrow{{{F}_{d}}}\uparrow \downarrow \overrightarrow{E} \\ \end{array} \right.$
+) Khi hệ quy chiếu chuyển động thẳng biến đổi đều với gia tốc $\vec{a}$ thì vật dao động của con lắc sẽ chịu thêm một lực quán tính:$\overrightarrow{{{F}_{qt}}}=-m\vec{a}$.
Thang máy đi lên, nhanh dần đều với gia tốc a: đi lên $\vec{v}\uparrow \xrightarrow{NDD}\vec{a}\uparrow \xrightarrow{{}}\overrightarrow{{{F}_{qt}}}\downarrow $
Thang máy đi lên, chậm dần đều với gia tốc a: đi lên $\vec{v}\uparrow \xrightarrow{CDD}\vec{a}\downarrow \xrightarrow{{}}\overrightarrow{{{F}_{qt}}}\uparrow $
Thang máy đi xuống, nhanh dần đều với gia tốc a: đi lên $\vec{v}\downarrow \xrightarrow{NDD}\vec{a}\downarrow \xrightarrow{{}}\overrightarrow{{{F}_{qt}}}\uparrow $
Thang máy đi xuống, chậm dần đều với gia tốc a: đi lên $\vec{v}\downarrow \xrightarrow{CDD}\vec{a}\uparrow \xrightarrow{{}}\overrightarrow{{{F}_{qt}}}\downarrow $
+) Nếu hệ quy chiếu quay đều với tốc độ $\omega $ thì vật chịu thêm lực li tâm có hướng ra tâm và có độ lớn: ${{F}_{\ell t}}=\frac{m{{v}^{2}}}{r}=m{{\omega }^{2}}r.$
I. BÀI TẬP MINH HỌA DẠNG 2
|
Bài tập 1: Một con lắc lò xo dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo với biên độ 4cm. Biết lò xo nhẹ có độ cứng 100 N/m và lấy gia tốc trọng trường g = 10 m/s2. Khi vật đến vị trí cao nhất, ta đặt nhẹ nhàng lên nó một gia trọng $\Delta m=150g$thì cả hai cùng dao động điều hòa. Biên độ dao động sau khi đặt là A. 2,5 cm B. 2 cm C. 5,5 cm D. 7cm |
Lời giải chi tiết
Khi chưa đặt gia trọng, có 2 lực tác dụng vào vật là $\overrightarrow{{{F}_{dh}}};\overrightarrow{P}$.
Sau khi đặt gia trọng, có 3 lực tác dụng vào vật: $\overrightarrow{{{F}_{dh}}};\overrightarrow{P}+\overrightarrow{\Delta P}$, vị trí cân bằng mới tại O’, O’ nằm dưới vtcb cũ O và cách O đoạn $O{O}’=\frac{\Delta P}{k}=\frac{0,15.10}{100}=0,015m=1,5cm$
Thời điểm đặt gia trọng lúc vật lên cao nhất $x=-A=-4cm$
|
Ngay trước |
Ngay sau |
|
O |
O’ |
|
v=0 |
v’=v=0 |
|
x = -4cm |
x’ = x + OO’ = -4 – 1,5 = -5,5 cm |
Do tại x’ có vận tốc v’ = 0 nên tại đó là biên dao động mới: ${A}’=\left| {{x}’} \right|=5,5cm.$. Chọn C
|
Bài tập 2: Hai vật A và B có cùng khối lượng 1 kg và có kích thước nhỏ được nối với nhau bởi sợi dây mảnh nhẹ dài 10 cm, hai vật được treo vào lò xo có độ cứng k = 100 N/m tại nơi có gia tốc trọng trường g = 10 m/s2, lấy ${{\pi }^{2}}=10$. Khi hệ vật và lò xo đang ở VTCB người ta đốt sợi dây nối hai vật và vật B sẽ rơi tự do còn vật A sẽ dao động điều hòa. Lần đầu tiên vật A lên đến vị trí cao nhất thì khoảng cách giữa hai vật bằng bao nhiêu? Biết rằng độ cao đủ lớn A. 70 cm B. 50 cm C. 80 cm D. 20 cm |
Lời giải chi tiết

Các lực tác dụng lên vật : $\overrightarrow{{{F}_{dh}}};\overrightarrow{{{P}_{A}}}+{{\overrightarrow{P}}_{B}}$
Sau khi đốt sợi dây, các lực tác dụng vào vật là $\overrightarrow{{{F}_{dh}}};\overrightarrow{{{P}_{A}}}$; Vị trí cân bằng mới tại O’, O’ nằm trên vtcb cũ O (do khối lượng của hệ vật giảm) và cách O đoạn:
$O{O}’=\frac{{{P}_{B}}}{k}=\frac{1.10}{100}=0,1m=10cm$
Thời điểm đốt dây là thời điểm hệ vật đứng yên tại vị trí cân bằng cũ (v=0) _ Tại đó li độ trong hệ dao động mới là x’= OO’=10 cm = A’
Khi A lên đến cao nhất tại biên âm ${{{x}’}_{A}}=-10cm$
Thời gian từ lúc cắt dây đến khi lên cao nhất = thời gian vật B rơi $=\frac{{{T}_{A}}}{2}=\frac{2\pi }{2}\sqrt{\frac{{{m}_{A}}}{k}}=\frac{\pi }{10}S$
Li độ của B lúc cắt dây: ${{x}_{OB}}=\ell +O{O}’=10+10=20cm=0,2m$
Quãng đường vật B rơi: ${{x}_{B}}^{\prime }={{x}_{OB}}+\frac{1}{2}g.{{t}^{2}}=0,2+\frac{1}{2}.10.{{\left( \frac{\pi }{10} \right)}^{2}}=0,7m=70cm$
_Khoảng cách của A và B lúc A lên cao nhất là: $d=\left| {{x}_{A}}^{\prime }-{{x}_{B}}^{\prime } \right|=80cm$. Chọn C
|
Bài tập 3: Một con lắc lò xo gồm vật nhỏ có khối lượng 100g và lò xo có độ cứng 40N/m được đặt trên mặt phẳng ngang không ma sát. Vật nhỏ đang nằm yên ở vị trí cân bằng, tại t = 0, tác dụng lực F = 2N lên vật nhỏ (hình vẽ) cho con lắc dao động điều hòa đến thời điểm $t=\pi /3s$thì ngừng tác dụng lực F. Dao động điều hòa của con lắc sau khi không còn lực F tác dụng có giá trị biên độ gần giá trị nào nhất sau đây? A. 9 cm B. 7 cm C. 5 cm D. 11 cm |
Lời giải chi tiết
Quá trình thêm lực: $\overrightarrow{{{F}_{dh}}}\xrightarrow[t=0]{{\vec{F}}}\left( \overrightarrow{{{F}_{dh}}}+\overrightarrow{{{F}_{{}}}} \right)$
Vtcb dịch sang bên phải (do lực F kéo sang phải): $O{O}’=\frac{F}{k}=5cm$
So với O’, vật có x’ = -5 cm. Do t = 0 có v = 0 => A’= 5cm
Tần số góc: $\omega =\sqrt{\frac{k}{m}}=20\,rad/s\Rightarrow T=\frac{\pi }{10}s$
Tách $t=\frac{\pi }{3}=\frac{10}{3}T=3T+\frac{T}{3}\Rightarrow {{{x}’}_{\left( t \right)}}=2,5cm$
Quá trình bớt lực: $\overrightarrow{{{F}_{dh}}}+\overrightarrow{F}\xrightarrow[t=\frac{\pi }{3}]{bot\vec{F}}\overrightarrow{{{F}_{dh}}}$
Ngừng tác dụng lực F thì vtcb của vật quay về O
|
Ngay trước |
Ngay sau |
|
O’ |
O |
|
${{{x}’}_{\left( t \right)}}=2,5cm$ |
${{x}’}’=O{O}’+{{{x}’}_{\left( t \right)}}=7,5cm$ |
|
${v}’=\frac{\sqrt{3}}{2}{{v}_{\max }}=\frac{\sqrt{3}}{2}.20.5=50\sqrt{3}cm/s$ |
${{v}’}’={v}’=50\sqrt{3}cm/s$ |
Biên độ dao động mới: ${{A}’}’=\sqrt{{{\left( \frac{50\sqrt{3}}{20} \right)}^{2}}+7,{{5}^{2}}}=5\sqrt{3}cm$. Chọn A
|
Bài tập 4: Một con lắc lò xo nằm ngang một đầu gắn với điểm cố định, một đầu gắn với vật nặng M, lò xo có độ cứng k = 80N/m. Ban đầu vật đứng yên ở vị trí lò xo tự nhiên. Sau đó người ta tác dụng một ngoại lực không đổi F = 4N. Sau khi vật đi được quãng đường là 6,4 cm kể từ thời điểm tác dụng ngoại lực thì dừng tác dụng ngoại lực. Biên độ dao động của con lắc sau đó là A. 7 cm B. 8 cm C. 9 cm D. 10 cm |
Lời giải chi tiết
Cách 1: Ta làm tương tự như ví dụ 8.
Cách 2: Sử dụng phương pháp năng lượng:
Tại t = 0, cơ năng của vật W = 0
Cơ năng của hệ lúc sau khi ngừng tác dụng lực: ${{W}’}’=\frac{1}{2}k{{{{A}’}’}^{2}}$
Có sự thay đổi năng lượng của hệ do lực $\vec{F}$ đã sinh công
Áp dụng biến thiên cơ năng: ${{W}’}’-W=F.s.\cos 0{}^\circ $
$\Rightarrow \frac{1}{2}k.{{{{A}’}’}^{2}}=Fs\Rightarrow {{A}’}’=\sqrt{\frac{2FS}{k}}=\sqrt{\frac{2.4.0,064}{80}}=0,08m=8cm$. Chọn B
|
Bài tập 5: Một lò xo nhẹ có độ cứng 100N/m, đầu trên gắn cố định đầu dưới treo quả cầu nhỏ có khối lượng m = 1kg sao cho vật có thể dao động không ma sát theo phương thẳng đứng trùng với trục của lò xo. Lúc đầu dùng bàn tay đỡ m để lò xo không biến dạng. Sau đó cho bàn tay chuyển động thẳng đứng xuống dưới nhanh dần đều với gia tốc $2m/{{s}^{2}}$. Bỏ qua mọi ma sát. Lấy gia tốc trọng trường $g=10\left( m/{{s}^{2}} \right)$. Khi m rời khỏi tay nó dao động điều hòa. Biên độ dao động điều hòa là A. 1,5 cm B. 2 cm C. 6 cm D. 1,2 cm |
Lời giải chi tiết

Tần số góc của con lắc m:
$\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{100}{1}}=10\,rad/s$
Định luật II Newton cho vật m:
$\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{{{F}_{dh}}}=ma$
Theo chiều của gia tốc: $P-N-{{F}_{dh}}=ma$
Tại vị trí vật m rời khỏi bàn tay thì N = 0
Vậy độ dãn của lò xo khi đó là
$\Delta \ell =\frac{mg-ma}{k}=\frac{1.10-1.2}{100}=8cm$
Vật và tay đã đi được một khoảng thời gian $t=\sqrt{\frac{2\Delta \ell }{a}}=\sqrt{\frac{2.0,08}{2}}=\frac{\sqrt{2}}{5}s$
Vận tốc của vật m ngay khi rời bàn tay sẽ là ${{v}_{o}}=at=\frac{2\sqrt{2}}{5}m/s=\frac{200\sqrt{2}}{5}cm/s$
Sau khi rời khỏi bàn tay vật m sẽ dao động điều hòa quanh vị trí cân bằng, tại vị trí này lò xo dãn một đoạn $\Delta {{\ell }_{o}}=mg/k=0,1m=10cm$
Biên độ dao động mới: $A=\sqrt{{{\left( \Delta \ell -\Delta {{\ell }_{o}} \right)}^{2}}+{{\left( \frac{{{v}_{o}}}{\omega } \right)}^{2}}}=\sqrt{{{\left( 8-10 \right)}^{2}}+{{\left( \frac{\frac{200\sqrt{2}}{5}}{10} \right)}^{2}}}=6cm$. Chọn C
|
Bài tập 6: Một con lắc lò xo nằm ngang gồm vật nặng khối lượng 100g, tích điện $q={{5.10}^{-6}}C$và lò xo có độ cứng k=10N/m. Khi vật đang ở vị trí cân bằng, người ta kích thích dao động bằng cách tạo ra một điện trường đều theo phương nằm ngang dọc theo trục của lò xo và có cường độ $E={{10}^{4}}V/m$trong khoảng thời gian $\Delta t=0,05\pi s$ rồi ngắt điện trường. Bỏ qua mọi ma sát. Tính năng lượng dao động của con lắc khi ngắt điện trường. A. 0,25 mJ B. 0,0375 J C. 0,025 J D. 0,0125J |
Lời giải chi tiết
Tần số dao động của con lắc $\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{10}{0,1}}=10\,rad/s$
Độ biến dạng của lò xo tại vị trí cân bằng $\Delta {{\ell }_{o}}=\frac{qE}{k}=\frac{{{5.10}^{-6}}{{.10}^{4}}}{10}={{5.10}^{-3}}m=0,5cm$
Dưới tác dụng của điện trường con lắc dao động với biên độ $A=\Delta {{\ell }_{o}}$
Sau khoảng thời gian $\Delta t=0,05\pi s\Leftrightarrow \Delta \varphi =\frac{\pi }{2}rad$vật đến vị trí $\left\{ \begin{array}{} x=0cm \\ {} v=A\omega =10.0,5=5cm/s \\ \end{array} \right.$
Sau khi ngắt điện trường con lắc dao động quanh vị trí cân bằng cũ với biên độ
${A}’=\sqrt{\left( x+\Delta {{\ell }_{o}}^{2} \right)+\frac{{{v}^{2}}}{{{\omega }^{2}}}}=\sqrt{{{\left( 0+0,5 \right)}^{2}}+{{\left( \frac{5}{10} \right)}^{2}}}=0,707cm$
Năng lượng dao động của con lắc khi ngắt điện trường $E=\frac{1}{2}k.{{{A}’}^{2}}=\frac{1}{2}.10.{{\left( \frac{0,707}{100} \right)}^{2}}=2,{{5.10}^{-4}}J$
Chọn A
|
Bài tập 7: Một con lắc lò xo đặt trên mặt phẳng ngang gồm lò xo nhẹ có một đầu cố định, đầu kia gắn với vật nhỏ mang điện tích q. Chu kì dao động của con lắc là 2s. Ban đầu được giữ ở vị trí lò xo bị giãn rồi thả nhẹ cho vật dao động khi thấy đi được quãng đường S vật có tốc độ là $6\pi \sqrt{2}cm/s$. Ngay khi vật trở lại vị trí ban đầu, người ta đặt một điện trường đều vào không gian xung quanh con lắc. Điện trường có phương song song với trục lò xo, có chiều hướng từ đầu cố định của lò xo đến vật, có cường độ lúc đầu là E V/m và cứ sau 2s thì cường độ điện trường lại tăng thêm E V/m. Biết sau 4s kể từ khi có điện trường vật đột nhiên ngừng dao động một lúc rồi mới lại dao động tiếp và trong 4s đó vật đi được quãng đường 3S. Bỏ qua mọi ma sát, điểm nối vật, lò xo và mặt phẳng ngang cách điện. Hỏi S gần giá trị nào nhất sau đây? A. 12,2 cm B. 10,5 cm C. 9,4 cm D. 6,1 cm |
Lời giải chi tiết
$T=2s\Rightarrow \omega =\pi rad/s$. Vị trí ban đầu giữ vật rồi thả là biên độ A
Độ biến dạng của lò xo tại vị trí cân bằng là $\Delta {{\ell }_{o}}=\frac{qE}{k}$
ð 2s đầu từ lúc đặt điện trường, CLLX dao động với vị trí cân bằng mới O1 sao cho $O{{O}_{1}}=\Delta {{\ell }_{o}}$
2s tiếp theo, dao động quanh vị trí cân bằng ${{O}_{2}}\left( {{O}_{1}}{{O}_{2}}=O{{O}_{1}} \right)$
2s tiếp theo, dao động quanh vị trí cân bằng ${{O}_{3}}\left( {{O}_{2}}{{O}_{3}}={{O}_{1}}{{O}_{2}}=O{{O}_{1}} \right)$
….
Sau 4s tức sau 2T kể từ khi có điện trường, vật về biên A và đột nhiên ngừng dao động, chứng tỏ ${{O}_{3}}\equiv A$
$\Rightarrow A=O{{O}_{1}}+{{O}_{1}}{{O}_{2}}+{{O}_{2}}{{O}_{3}}=3\Delta {{\ell }_{o}}\Rightarrow \Delta {{\ell }_{o}}=\frac{A}{3}$
Quãng đường đi được trong 4s này bằng $4.\frac{2A}{3}+4.\frac{A}{3}=4A=3S\Rightarrow S=\frac{4A}{3}$

Ban đầu vật đi được S = 4A/3 tới vị trí x= -A/3cm, vật có tốc độ $v=6\pi \sqrt{2}cm/s$nên
$\frac{{{x}^{2}}}{{{A}^{2}}}+\frac{{{v}^{2}}}{{{\left( A\omega \right)}^{2}}}=1\Leftrightarrow \frac{{{\left( -A/3 \right)}^{2}}}{{{A}^{2}}}+\frac{{{\left( 6\pi \sqrt{2} \right)}^{2}}}{{{A}^{2}}{{\pi }^{2}}}=1\Rightarrow A=9cm\Rightarrow S=\frac{4A}{3}=\frac{4.9}{3}=12cm$. Chọn A
|
Bài tập 8: Con lắc lò xo có độ cứng 10N/m và vật nặng m = 2/15 kg, chỉ có thể dao động không ma sát dọc theo trục Ox nằm ngang trùng với trục của lò xo. Vật ${{m}_{o}}=4/15$kg được tích điện $q={{10}^{-4}}C$, gắn cách điện với m. Vật mo sẽ bong ra nếu lực kéo tác dụng lên nó đạt giá trị 0,5N. Đặt điện trường đều, có độ lớn E, có phương trùng với trục Ox, có chiều hướng từ điểm cố định của lò xo đến vật. Đưa hệ đến vị trí lò xo nén một đoạn 10cm rồi buông nhẹ để hệ dao động ở thời điểm t =0. Đến thời điểm $t=2\pi /5s$ thì mo tách ra khỏi m. Độ lớn E bằng A. 10000/3 V/m B. 10000/11 V/m C. 1250 V/m D. 5000V/m |
Lời giải chi tiết

Tính được ${{x}_{1}}=\frac{qE}{k}\Rightarrow k{{x}_{1}}=qE$
$T=2\pi \sqrt{\frac{m+{{m}_{o}}}{k}}=\frac{2\pi }{5}s=\frac{T}{3}=\frac{T}{4}+\frac{T}{12}$
Hai vật bắt đầu tách ra tại N:
+) Độ lớn lực đàn hồi:
${{F}_{dh}}=k.\Delta \ell =0,5.k.{{x}_{M}}+1,5.k.{{x}_{1}}=0,5+1,5qE$
+) Gia tốc $a=\frac{qE={{F}_{\ell k}}}{{{m}_{o}}}=\frac{{{F}_{\ell k}}-{{F}_{dh}}}{m}$
$\Leftrightarrow \frac{qE-0,5}{2}=\frac{0,5-0,5-1,5qE}{1}$
$\Rightarrow E=\frac{0,5}{4q}=1250\,V/m$. Chọn C
|
Bài tập 9: Hai lò xo có độ cứng lần lượt là ${{k}_{1}}=100\,N/m$và ${{k}_{2}}=150\,N/m$. Treo vật khối lượng m = 250g vào hai lò xo ghép song song. Kéo vật xuống dưới vị trí cân bằng 1 đoạn $4/\pi $cm rồi thả nhẹ. Khi vật qua vị trí cân bằng thì lò xo 2 bị đứt. Biên độ dao động của vật sau khi lò xo 2 bị đứt là A. 3,5 cm B. 2 cm C. 2,5 cm D. 3 cm |
Lời giải chi tiết

Gọi OC là vtcb của vật khi hệ 2 lò xo, tại đó hệ dãn một đoạn:
$\Delta {{\ell }_{C}}=\frac{mg}{{{k}_{1}}+{{k}_{2}}}=\frac{0,25.10}{100+150}=0,01m=1cm$
Gọi Om là vtcb của vật khi chỉ còn k1, lúc độ dãn của riêng k1 là:
$\frac{mg}{{{k}_{1}}}=0,025m=2,5cm$
Vậy $b={{O}_{C}}{{O}_{m}}=1,5cm$
+) Đối với hệ 2 lò xo, kéo m xuống dưới vtcb một đoạn $4/\pi $ cm rồi thả nhẹ thì A = $4/\pi $cm
_ Lúc đi qua vtcb OC thì có vận tốc là:
$v=A\omega =\sqrt{\frac{{{k}_{1}}+{{k}_{2}}}{m}.A}=40\,cm/s$
+) Ngay tại vị trí OC này k2 đứt, con lắc bây giờ là con lắc mới gồm k1 và m. Đối với con lắc này vtcb mới là Om và vật m đi qua vị trí O có $x=\pm 1,5cm$ với v = 40 cm/s tần số mới là ${\omega }’=\sqrt{\frac{{{k}_{1}}}{m}}=20$rad/s
$\Rightarrow {A}’=\sqrt{{{x}^{2}}+{{\left( \frac{v}{{{\omega }’}} \right)}^{2}}}=\sqrt{1,{{5}^{2}}+{{\left( \frac{40}{20} \right)}^{2}}}=2,5cm$. Chọn C
|
Bài tập 10: Cho cơ hệ như hình vẽ bên. Vật m khối lượng 100g có thể chuyển động tịnh tiến, không ma sát trên mặt phẳng nằm ngang dọc theo trục lò xo có k = 40N/m. Vật M khối lượng 300g có thể trượt trên m với hệ số ma sát $\mu =0,2$. Ban đầu, giữ m đứng yên ở vị trí lò xo dãn 4,5cm, dây D (mềm, nhẹ, không giãn) song song với trục lò xo. Biết M luôn ở trên m và tiếp xúc giữa hai vật nằm ngang. Lấy $g=10m/{{s}^{2}}$. Thả nhẹ cho m chuyển động. Tính từ lúc thả đến khi m đổi chiều chuyển động lần thứ 2 thì tốc độ trung bình của m là A. 2,23 cm/s B. 19,1 cm/s C. 28,7 cm/s D. 33,4 cm/s |
Lời giải chi tiết
Lực ma sát trượt giữa M và m chỉ tồn tại khi D căng _ tương ứng với chuyển động của m về phía bên trái. Do vậy, ta chia quá trình chuyển động của m thành các giai đoạn sau:
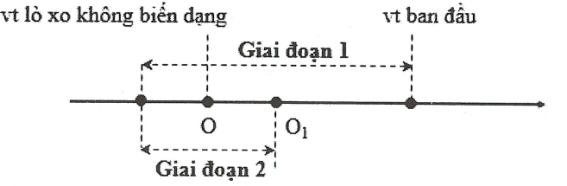
Giai đoạn 1: Dao động tắt dần quanh vị trí cân bằng tạm O1
Tại vtcb tạm, lực đàn hồi cân bằng với lực ma sát:
$k\Delta {{\ell }_{o}}=\mu Mg\Rightarrow \Delta {{\ell }_{o}}=\frac{\mu Mg}{k}=\frac{0,2.0,3.10}{40}=1,5cm$
_Biên độ giai đoạn này ${{A}_{1}}=4,5-1,5=3cm$
Vật chuyển động đến biên thì đổi chiều lúc này lò xo bị nén 1 đoạn $\Delta \ell =3-1,5=1,5cm$
Thời gian tương ứng trong giai đoạn này ${{t}_{1}}=\frac{{{T}_{1}}}{2}=\pi \sqrt{\frac{m}{k}}=\pi \sqrt{\frac{0,1}{40}}=0,05\pi s$
Giai đoạn 2: m đổi chiều chuyển động _ dây chùng không còn ma sát trượt nữa _ hệ vật m + M dao động điều hòa quanh vtcb O (vt lò xo không biến dạng)
Biên độ dao động của vật ở giai đoạn này $A{{ {} }_{2}}=1,5cm$(${{A}_{2}}<{{A}_{2\max }}=\frac{\mu g}{{{\omega }_{2}}^{2}}=2cm$ để M không trượt trong quá trình dao động)
Thời gian tương ứng đến khi vật đổi chiều lần thứ hai${{t}_{2}}=\frac{{{T}_{2}}}{2}=\pi \sqrt{\frac{m+M}{k}}=\pi \sqrt{\frac{0,1+0,3}{40}}=0,1\pi s$
_ Tốc độ trung bình của m trong 2 giai đoạn trên:
${{v}_{tb}}=\frac{S}{t}=\frac{2{{A}_{1}}+2{{A}_{2}}}{{{t}_{1}}+{{t}_{2}}}=\frac{2\left( 3+1,5 \right)}{0,05\pi +0,1\pi }=19,1\,cm/s$. Chọn B
|
Bài tập 11: Một con lắc lò xo được treo trên trần một thang máy. Khi thang máy đứng yên thì con lắc lò xo dao động điều hòa với chu kì T =0,4s và biên độ A = 5cm. Vừa lúc quả cầu con lắc đang đi qua vị trí lò xo không biến dạng theo chiều từ trên xuống thì thang máy chuyển động nhanh dần đều đi lên với gia tốc $a=5m/{{s}^{2}}$. Lấy $g=10m/{{s}^{2}}$. Biên độ dao động của con lắc lò xo lúc này A. $5\sqrt{3}$cm B. 5 cm C. $3\sqrt{5}$ cm D. 7 cm |
Lời giải chi tiết

Tần số góc $\omega =\frac{2\pi }{T}=5\pi \,rad/s$
Độ dãn của lò xo tại VTCB lúc thang máy đứng yên: $\Delta {{\ell }_{o}}=\frac{mg}{k}=\frac{g}{{{\omega }^{2}}}=4cm$
Tại thời điểm vật đi qua vị trí lò xo không biến dạng (nó có li độ so với vị trí cân bằng cũ là
${{x}_{c}}=+4cm$ và c


