VẤN ĐỀ 2: CẢM ỨNG ĐIỆN TỪ.
LÝ THUYẾT TRỌNG TÂM
|
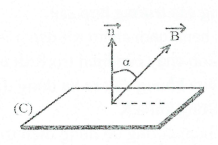
1. Từ thông: Đại lượng diễn tả số lượng đường sức từ xuyên qua một vòng dây kín (C) (diện tích S). Xét một khung dây gồm N vòng có diện tích S, nằm trong một từ trường đều, sao cho đường sức từ $\overrightarrow{B}$ hợp với vector pháp tuyến dương $\left( \overrightarrow{n} \right)$ một góc $\alpha $ . Từ thông $\Phi $ là đại lượng được định nghĩa |
|
|
bằng công thức: $\Phi =NBS.\cos \alpha $ |
|
– Ý nghĩa của từ thông: Từ thông diễn tả số đường sức từ xuyên qua một điện tích nào đó.
– Đơn vị: Vê-be (Wb).
2. Hiện tượng cảm ứng điện từ
– Khi có sự biến đổi từ thông qua một mặt giới hạn bởi một mạch kín (vd: khung dây kín có diện tích S) thì trong mạch xuất hiện một dòng điện cảm ứng.
– Hiện tượng xuất hiện dòng điện cảm ứng trong một mạch kín khi có sự biến thiên từ thông qua mạch kín này được gọi là hiện tượng cảm ứng điện từ.
3. Xác định chiều dòng điện cảm ứng bằng định luật Len-xơ: Dòng điện cảm ứng xuất hiện trong một mạch kín có chiều sao cho từ trường cảm ứng có tác dụng chống lại sự biến thiên từ thông ban đầu qua mạch kín đó.
4. Suất điện động cảm ứng là suất điện động sinh ra dòng điện cảm ứng. Kí hiệu : ${{e}_{c}}$
${{e}_{C}}=-\frac{\Delta \Phi }{\Delta t}$
Với $\Delta \Phi $ : độ biến thiên từ thông qua mạch kín (Wb), $\Delta \Phi ={{\Phi }_{2}}-{{\Phi }_{1}}$
$\Delta t$ : thời gian từ thông biến thiên qua mạch (s)
“$-$” : dấu trừ biểu thị định luật Len-xơ
(Độ lớn) suất điện động cảm ứng là đại lượng đặc trưng cho tốc độ biến thiên của từ thông được xác định bởi biểu thức: $\left| {{e}_{C}} \right|=\left| \frac{\Delta \Phi }{\Delta t} \right|=\left| \frac{{{\Phi }_{2}}-{{\Phi }_{1}}}{{{t}_{2}}-{{t}_{1}}} \right|$ (chiều áp dụng định lý Lenxo)
CÁC DẠNG BÀI TẬP
DẠNG 1: XÁC ĐỊNH CHIỀU DÒNG ĐIỆN CẢM ỨNG ${{I}_{C}}$.
LÝ THUYẾT CHUNG
Dòng điện cảm ứng xuất hiện trong một mạch kín có chiều sao cho từ trường cảm ứng có tác dụng chống lại sự biến thiên từ thông ban đầu qua mạch kín đó.
Bước 1: Vẽ $\overrightarrow{B}$ của dụng cụ còn lại (không phải dụng cụ mà đề yêu cầu xác định ${{I}_{C}}$ ). Cụ thể:
+) Nam châm: $\overrightarrow{B}$ ra cực Bắc (N), vào cực Nam (S).
+) Dây dẫn thẳng dài: Dùng quy tắc nắm bàn tay phải 1:
“Giơ ngón cái của bàn tay phải hướng theo chiều dòng điện, khum bốn ngón kia xung quanh dây dẫn thì chiều từ cổ tay đến các ngon tay là chiều của đường sức từ”.
+) Vòng dây tròn, ống dây dài: Dùng quy tắc bàn tay phải 2:
“Khum tay phải theo vòng dây của khung sao cho chiều từ cổ tay đến các ngón tay trùng với chiều dòng điện trong khung, ngón cái choãi ra chỉ chiều các đường sức từ xuyên qua mặt phẳng dòng điện”.
Bước 2: Xét từ thông qua $\overrightarrow{B}$ qua Nam châm, Dây dẫn thẳng, Vòng dây tròn hay Ống dây,… tăng hay giảm
+) Nếu $\Phi $ tăng thì $\overrightarrow{{{B}_{c}}}$ ngược chiều $\overrightarrow{B}$ , nếu $\Phi $ giảm thì $\overrightarrow{{{B}_{c}}}$ cùng chiều $\overrightarrow{B}$ .
+) Quy tắc chung: gần ngược – xa cùng. Nghĩa là khu nam châm hay khung dây lại gần nhau thì $\overrightarrow{{{B}_{c}}}$ và $\overrightarrow{B}$ ngược. Còn khi ra xa nhau thì $\overrightarrow{{{B}_{c}}}$ và $\overrightarrow{B}$ ngược
Bước 3: Xác định dòng điện cảm ứng sinh ra trong khung dây theo qui tắc nắm bàn tay phải.
VÍ DỤ MINH HỌA
|
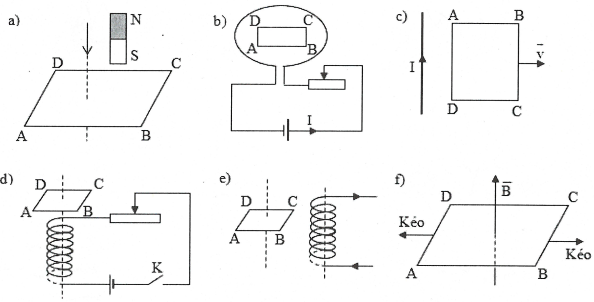
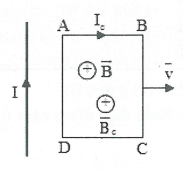
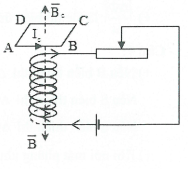
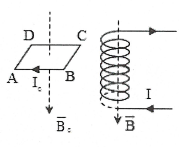
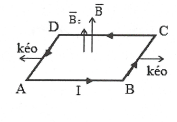
Bài tập minh họa: Dùng định luật Len-xơ xác định chiều dòng điện cảm ứng trong khung dây dẫn trong các trường hợp sau: a) Thanh nam châm rơi đến gần khung dây, sau đó đi qua khung dây và rơi ra khỏi khung dây. b) Con chạy của biến trở R di chuyển sang phải. c) Đưa khung dây ra xa dòng điện. d) Đóng khóa K. e) Giảm cường độ dòng điện trong ống dây. f) Khung dây ban đàu trong từ trường hình vuông, sau đó dược kéo thành hình chữ nhật ngày càng dẹt đi. |
Lời giải chi tiết:
|
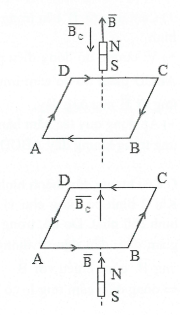
a) Thanh nam châm rơi đến gần khung dây, sau đó đi qua khung dây và rơi ra khỏi khung dây: +) Cảm ứng từ $\overrightarrow{B}$ của nam châm có hướng vào S ra N. +) Khi nam châm rơi lại gần khung dây ABCD thì cảm ứng từ cảm ứng $\overrightarrow{{{B}_{c}}}$ của khung dây có chiều ngược với cảm ứng từ $\overrightarrow{B}$ . Áp dụng quy tắc nắm bàn tay phải suy ra dòng điện cảm ứng trong khung dây ABCD có chiều từ $A\to D\to C\to B\to A$ như hình. +) Sau khi nam châm qua khung dây thì nam châm sẽ ra xa dần khung dây nên lúc này cảm ứng từ cảm ứng $\overrightarrow{{{B}_{c}}}$ của khung có chiều cùng với cảm ứng từ $\overrightarrow{B}$ . Áp dụng quy tắc nắm bàn tay phải suy ra dòng điện cảm ứng trong khung dây ABCD có chiều từ $A\to B\to C\to D\to A$ . |
|
|
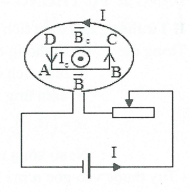
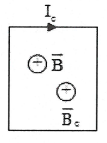
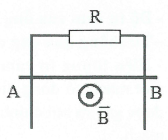
b) Con chạy của biến trở R di chuyển sang phải: +) Dòng điện tròn sinh ra cảm ứng từ $\overrightarrow{B}$ có chiều từ trong ra ngoài. +) Khi biến trở dịch chuyển sang phải thì điện trở R tăng nên dòng điện I trong mạch giảm $\to $ cảm ứng từ $\overrightarrow{B}$ do vòng dây trong sinh ra cũng giảm $\to $ từ thông giảm $\to $ từ trường cảm ứng $\overrightarrow{{{B}_{c}}}$ sẽ cùng chiều với từ trường của dòng điện tròn (chiều từ trong ra ngoài). +) Áp dụng quy tắc nắm bàn tay phải: chiều của dòng điện cảm ứng trong khung dây ABCD có chiều từ $A\to B\to C\to D\to A$. |
|
|
c) Đưa khung dây ra xa dòng điện: +) Cảm ứng từ $\overrightarrow{B}$ do dòng điện I gây ra ở khung dây ABCD có chiều từ ngoài vào trong. +) Vì khung dây ra xa dòng điện I nên từ thông giảm $\to $ từ trường cảm ứng ${{\overrightarrow{B}}_{c}}$ của khung dây sẽ cùng chiều với từ trường $\overrightarrow{B}$ . +) Áp dụng quy tắc nắm bàn tay phải: chiều của dòng điện cảm ứng |
|
|
trong khung dây ABCD có chiều từ $A\to B\to C\to D\to A$ . |
|
|
d) Đóng khóa K: +) Khi đóng khóa K trong mạch có dòng điện I tăng từ 0 đến I +) Áp dụng quy tắc nắm bàn tay phải xác định được chiều cảm ứng từ $\overrightarrow{B}$ bên trong ống dây có chiều như hình. +) Vì dòng điện có cường độ tăng từ 0 đến I nên từ thông cũng tăng $\Rightarrow $ chiều cảm ứng từ cảm ứng $\overrightarrow{{{B}_{c}}}$ ngược với chiều cảm ứng từ $\overrightarrow{B}$ . +) Áp dụng quy tắc nắm bàn tay phải: chiều của dòng điện cảm ứng trong khung dây ABCD có chiều từ $A\to B\to C\to D\to A$ . |
|
|
e) Giảm cường độ dòng điện trong ống dây: +) Cảm ứng từ $\overrightarrow{B}$ bên trong ống dây có chiều từ trên xuống như hình. +) Vì cường độ dòng điện giảm nên từ thông gửi qua khung dây ABCD giảm do đó cảm ứng từ cảm ứng $\overrightarrow{{{B}_{c}}}$ cùng chiều với cảm ứng từ $\overrightarrow{B}$ của ống dây. +) Áp dụng quy tắc nắm bàn tay phải: chiều của dòng điện cảm ứng trong khung dây ABCD có chiều dài từ $A\to D\to C\to B\to A$ . |
|
|
f) Kéo khung dây thành hình chữ nhật ngày càng dẹt đi: Khi 2 hình có cùng chu vi thì hình vuông có diện tích lớn hơn hình chữ nhật. Do đó, trong quá trình kéo thì diện tích của khung giảm dần, dẫn đến từ thông qua khung giảm $\Rightarrow $ từ trường cảm ứng $\overrightarrow{{{B}_{c}}}$ cùng chiều với $\overrightarrow{B}$ $\Rightarrow $ dòng điện cảm ứng ${{I}_{C}}$ có chiều $A\to B\to C\to D\to A$ . |
|
DẠNG 2: TỪ THÔNG – SUẤT ĐIỆN ĐỘNG CẢM ỨNG.
LÝ THUYẾT CHUNG
1. Từ thông qua diện tích S đặt trong từ trường: $\Phi =NB\text{S}\cos \alpha $
Trong đó: $\Phi $ : từ thông qua mạch kín (Wb)
S: diện tích của mạch (${{m}^{2}}$)
B: cảm ứng từ gửi qua mạch (T)
$\alpha =\left( \overrightarrow{B},\overrightarrow{n} \right)$ , $\overrightarrow{n}$ là pháp tuyến của mạch kín
N: số vòng dây của mạch kín.
– Tùy thuộc vào góc $\alpha $ mà từ thông có thể có giá trị âm hoặc dương:
+) khi ${{0}^{\circ }}<\alpha 0$ thì $\Phi $ dương
+) Khi ${{90}^{\circ }}<\alpha <{{180}^{\circ }}\Rightarrow \cos \alpha <0$ thì $\Phi $ âm
+) Khi $\alpha ={{90}^{\circ }}\Rightarrow \cos \alpha =0$ thì $\Phi =0$
+) Khi $\alpha ={{0}^{\circ }}\Rightarrow \cos \alpha =1$ thì ${{\Phi }_{\max }}=BS$
+) Khi $\alpha ={{180}^{\circ }}\Rightarrow \cos \alpha =-1$ thì ${{\Phi }_{\min }}=-B\text{S}$
$\Rightarrow -BS\le \Phi \le BS$
2. Suất điện động cảm ứng trong khung dây
${{e}_{c}}=-N\frac{\Delta \Phi }{\Delta t}\Rightarrow \left| {{e}_{c}} \right|=N\frac{\left| \Delta \Phi \right|}{\Delta t}$
+) $\left| {{e}_{C}} \right|$ là suất điện động cảm ứng (V)
+) $\frac{\left| \Delta \Phi \right|}{\Delta t}$ là tốc độ biến thiên từ thông $\left( \frac{\text{W}b}{s} \right)$ hoặc (V)
– Chú ý:
+) Nếu B biến thiên thì $\Delta \Phi =S.\cos \alpha .\Delta B=S.cos\alpha .\Delta \left( {{B}_{2}}-{{B}_{1}} \right)$
Nếu S biến thiên thì $\Delta \Phi =B.\cos \alpha .\Delta S=B.cos\alpha .\Delta \left( {{S}_{2}}-{{S}_{1}} \right)$
Nếu $\alpha $ biến thiên thì $\Delta \Phi =B.S.\Delta \left( \cos \alpha \right)=B.S.\Delta \left( \cos {{\alpha }_{2}}-\cos {{\alpha }_{1}} \right)$
+) Khi nói mặt phẳng khung dây hợp với cảm ứng từ $\overrightarrow{B}$ một góc $\beta $ thì $\alpha =90\pm \beta $
+) Cường độ dòng điện cảm ứng qua mạch kín: ${{i}_{C}}=\frac{{{e}_{C}}}{R}$ với R là điện trở khung dây.
VÍ DỤ MINH HỌA
|
Bài tập 1: Một khung dây phẵng diện tích 20 $c{{m}^{2}}$ , gồm 10 vòng được đặt trong từ trường đều. Véc tơ cảm ứng từ làm thành với mặt phẵng khung dây góc 30° và có độ lớn bằng ${{2.10}^{-4}}T$. Người ta làm cho từ trường giảm đều đến 0 trong thời gian 0,01 s. Tính suất điện động cảm ứng xuất hiện trong khung dây trong thời gian từ trường biến đổi. |
Lời giải chi tiết:
Ta có: ${{e}_{c}}=-\frac{\Delta \Phi }{\Delta t}=\frac{0-NBS\cos \left( \overrightarrow{n},\overrightarrow{B} \right)}{\Delta t}={{2.10}^{-4}}V$ .
|
Bài tập 2: Cuộn dây có N = 100 vòng, diện tích mỗi vòng S = 300 $c{{m}^{2}}$ có trục song song với $\overrightarrow{B}$ của từ trường đều, B = 0,2 T. Quay đều cuộn dây để sau $\Delta t=0,5$s, trục của nó vuông góc với $\overrightarrow{B}$ . Tính suất điện động cảm ứng trung bình trong cuộn dây. |
Lời giải chi tiết:
+) Ban đầu:
Trục của vòng dây song song với B nên:${{\alpha }_{1}}=\left( \overrightarrow{n};\overrightarrow{B} \right)=0$
Từ thông qua N vòng dây lúc đầu: ${{\Phi }_{1}}=NBS\cos {{\alpha }_{1}}=N{{B}_{1}}S$
+) Lúc sau:
Trục của vòng dây vuông góc với $\overrightarrow{B}$ nên: ${{\alpha }_{2}}=\left( \overrightarrow{n};\overrightarrow{B} \right)={{90}^{\circ }}$
Từ thông qua N vòng dây lúc sau: ${{\Phi }_{2}}=NBS\cos {{\alpha }_{2}}=0$
Độ biến thiên từ thông: $\Delta \Phi ={{\Phi }_{2}}-{{\Phi }_{1}}=-{{\Phi }_{1}}=-NBS$
Độ lớn suất điện động: $\left| e \right|=\left| \frac{\Delta \Phi }{\Delta t} \right|=\left| \frac{NBS}{\Delta t} \right|=\left| \frac{100.0,{{2.300.10}^{-4}}}{0,5} \right|=1,2V$
|
Bài tập 3: Một ống dây hình trụ dài gồm N = 1000 vòng dây, diện tích mỗi vòng dây S = 100 $c{{m}^{2}}$ . Ống dây có R = 16$\Omega $ , hai đầu nối đoản mạch và được đặt trong từ trường đều: vectơ cảm ứng từ $\overrightarrow{B}$ song song với trục của hình trụ và độ lớn tăng đều 0,04 T/s. Tính công suất tỏa nhiệt trong ống dây |
Lời giải chi tiết:
Từ thông qua ống dây: $\Phi =NBS\cos {{0}^{\circ }}=NBS$
Tốc độ biến thiên từ thông: $\frac{\Delta \Phi }{\Delta t}=\frac{\Delta \left( NBS \right)}{\Delta t}=NS\frac{\Delta B}{\Delta t}$
Độ lớn suất điện động trong khung dây:
$\left| e \right|=\left| \frac{\Delta \Phi }{\Delta t} \right|=NS\left| \frac{\Delta B}{\Delta t} \right|=1000.\left( {{100.10}^{-4}} \right).0,04=0,4\left( V \right)$
Dòng điện cảm ứng trong ống dây: ${{i}_{c}}=\frac{e}{R}=\frac{0,4}{16}=\frac{1}{40}\left( A \right)$
Công suất tỏa nhiệt trên R: $P={{i}^{2}}R={{\left( \frac{1}{40} \right)}^{2}}.16=0,01\left( W \right)$ .
|
Bài tập 4: Vòng dây đồng $\left( \rho =1,{{75.10}^{-8}}\Omega .m \right)$ đường kính d = 20 cm, tiết diện ${{S}_{0}}=5$$m{{m}^{2}}$ đặt vuông góc với $\overrightarrow{B}$ của từ trường đều. Tính độ biến thiên $\frac{\Delta B}{\Delta t}$ của cảm ứng từ khi dòng điện cảm ứng trong vòng dây là I = 2A. |
Lời giải chi tiết:
Suất điện động cảm ứng xuất hiện trong vòng dây có độ lớn:
$\left| e \right|=\left| \frac{\Delta \Phi }{\Delta t} \right|=\left| \frac{S.\Delta B}{\Delta t} \right|=S.\left| \frac{\Delta B}{\Delta t} \right|=\frac{\pi {{d}^{2}}}{4}.\frac{\Delta B}{\Delta t}$
Điện trở của vòng dây: $R=\rho \frac{L}{{{S}_{0}}}=\rho \frac{\pi d}{{{S}_{0}}}$
Cường độ dòng điện cảm ứng qua vòng dây: $I=\frac{\left| e \right|}{R}=\frac{\frac{\pi {{d}^{2}}}{4}\left| \frac{\Delta B}{\Delta t} \right|}{\rho \frac{\pi d}{{{S}_{0}}}}=\frac{{{S}_{0}}.d}{4\rho }.\frac{\Delta B}{\Delta t}$
$\Rightarrow \frac{\Delta B}{\Delta t}=\frac{4\rho I}{S.d}=\frac{4.1,{{75.10}^{-8}}.2}{{{5.10}^{-6}}.0,2}=0,14\left( {T}/{s}\; \right)$ .
|
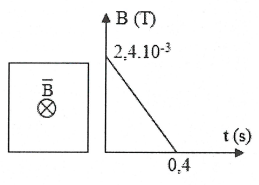
Bài tập 5: Một khung dây cứng, phẳng diện tích 25$c{{m}^{2}}$, gồm 10 vòng dây. Khung dây được đặt trong từ trường đều. Khung dây nằm trong mặt phẳng như hình vẽ. Cảm ứng từ biến thiên theo thời gian theo độ thị như hình bên. a) Tính độ biến thiên của từ thông qua khung dây kể từ lúc t = 0 đến t = 0,4s. b) Xác định giá trị của suất điện động cảm ứng trong khung. c) Tìm chiều của dòng điện cảm ứng trong khung. |
|
Lời giải chi tiết:
|
a) Độ biến thiên của từ thông qua khung dây kể từ lúc ${{t}_{1}}=0$ đến ${{t}_{2}}=0,4\text{s}$ . Từ đồ thị ta có: $\left\{ \begin{array}{} {{t}_{1}}=0\Rightarrow {{B}_{1}}=2,{{4.10}^{-3}}\left( T \right) \\ {} {{t}_{2}}=0,4s\Rightarrow {{B}_{2}}=0 \\ \end{array} \right.$ Độ biến thiên cảm ứng từ: $\Delta B={{B}_{2}}-{{B}_{1}}=-2,{{4.10}^{-3}}\left( T \right)$ Khung dây vuông góc với mặt phẳng khung dây nên: $\alpha =\left( \overrightarrow{n};\overrightarrow{B} \right)=0$ Độ biến thiên từ thông qua khung dây: $\Delta \Phi =N.\left( \Delta B \right).S.\cos \alpha =10.\left( -2,{{4.10}^{-3}} \right){{.25.10}^{-4}}.I=-{{6.10}^{-5}}\left( Wb \right)$ Vậy từ thông giảm một lượng $\left| \Delta \Phi \right|={{6.10}^{-5}}\left( Wb \right)$ b) Suất điện động cảm ứng trong khung dây: ${{e}_{c}}=-\frac{\Delta \Phi }{\Delta t}=1,{{5.10}^{-4}}\left( V \right)$ |
|
c) Vì từ thông giảm nên vecto cảm ứng từ $\overrightarrow{{{B}_{c}}}$ cùng chiều với cảm ứng từ $\overrightarrow{B}$ . Áp dụng quy tắc nắm bàn tay phải suy ra chiều của dòng điện cảm ứng là chiều kim đồng hồ (hình vẽ).
DẠNG 3: SUẤT ĐIỆN ĐỘNG CẢM ỨNG TRONG THANH.
LÝ THUYẾT CHUNG
Khi đoạn dây dẫn chuyển động cắt các đường sức từ thì trong đoạn dây đó xuất hiện suất điện động (đóng vai trò như nguồn điện). Suất điện động trong trường hợp này cũng gọi là suất điện động cảm ứng.
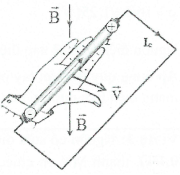
Quy tắc bàn tay phải:
– Đặt bàn tay phải hứng các đường sức từ, ngón tay cái choãi ra 90° chỉ chiều chuyển động của đoạn dây, khi đó đoạn dây dẫn đóng vai trò như một nguồn điện, chiều từ cổ tay đến ngón tay giữa chỉ chiều từ cực âm sang cực dương của nguồn điện đó:
– Chú ý:
+) Khi mạch được nối kín thì trong mạch có dòng điện cảm ứng ${{i}_{c}}$ .
+) Bên trong nguồn điện, dòng điện có chiều từ cực âm sang cực dương, bên ngoài thì ngược lại.
Biểu thức suất điện động cảm ứng từ trong đoạn dây:
– Xét trường hợp đơn giản từ trường $\overrightarrow{B}$ vuông góc với mặt khung dây, khi đó suất điện động trong khung dây được tính theo công thức:
$\left\{ \begin{array}{} {{e}_{c}}=\left| \frac{\Delta \Phi }{\Delta t} \right|=\frac{B.\left| \Delta S \right|}{\Delta t} \\ {} \Delta S=\ell .s=\ell v.\Delta t \\ \end{array} \right.\Rightarrow \left| {{e}_{c}} \right|=B\ell v$
Trong trường hợp $\overrightarrow{B}$ và $\overrightarrow{v}$ hợp với nhau một góc $\alpha $ thì:$\left| e{{ {} }_{c}} \right|=Bv\ell \sin \alpha $
– Chú ý:
+) Khi mạch kín thì dòng cảm ứng chạy trong dây dẫn có điện trở R: ${{i}_{c}}=\frac{{{e}_{c}}}{R}$
+) Khi trong mạch có hai dòng điện thì số chỉ Ampe kế sẽ là tổng đại số hai dòng điện (hai dòng điện ở đây chính là dòng I do nguồn E tạo ra và dòng ${{i}_{c}}$ do hiện tượng cảm ứng điện từ tạo ra).
VÍ DỤ MINH HỌA
|
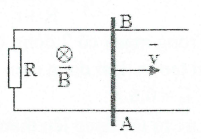
Bài tập 1: Thanh kim loại AB dài 20 cm kéo trượt đều trên hai thanh ray kim loại nằm ngang như hình vẽ. Các dây nối nhau bằng bằng điện trở $R=3\Omega $ . Vận tốc của thanh AB là 12 m/s. Hệ thống đặt trong từ trường đều có B = 0,4 T, $\overrightarrow{B}$vuông góc với mạch điện. a) Tìm suất điện động cảm ứng trong khung. b) Cường độ dòng điện cảm ứng và cho biết chiều. |
|
Lời giải chi tiết:
a) Suất điện động cảm ứng trong thanh: ${{e}_{c}}=B.v.\ell \sin \alpha =0,4.0,2.2.12.\sin {{90}^{\circ }}=0,96V$
b) Dòng điện trong mạch: ${{I}_{c}}=\frac{{{e}_{c}}}{R}=0,32A$
Quy tắc bàn tay phải $\Rightarrow $ chiều của dòng điện cảm ứng đi qua thanh AB theo chiều từ A đến B.
|
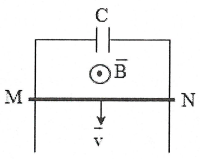
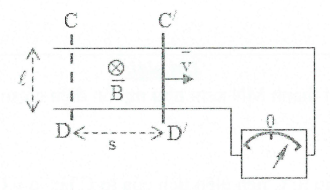
Bài tập 2: Cho hệ thống như hình vẽ, thanh MN có chiều dài 50 cm chuyển động với tốc độ 10 m/s trong từ trường đều B = 0,25 T. Tụ điện có điện dung C = 10 $\mu F$ . Tính độ lớn diện tích của của tụ điện và cho biết bản nào tích điện dương. |
|
Lời giải chi tiết:
Khi thanh MN chuyển động thì thanh MN xem như nguồn điện có suất điện động có độ lớn là: $e=Bv\ell =1,25\left( V \right)$
Nguồn điện MN sẽ nạp điện cho tụ C nên điện tích của tụ C là: $q=C.e=12,5\left( \mu C \right)$
Áp dụng quy tắc bàn tay phải suy ra N là cực âm M là cực dương của nguồn điện. Do đó bản M sẽ mang điện tích dương, bản N mang điện tích âm.
|
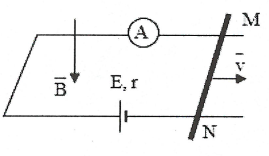
Bài tập 3: Nguồn có suất điện động E = 1,5V, điện trở trong r = 0,1$\Omega $, thanh MN có chiều dài 1 m có điện trở $R=2,9\Omega $. Từ trường $\overrightarrow{B}$ có phương thẳng đứng, hướng xuống và vuông góc với mặt khung như hình vẽ và B = 0,1 T. Thanh MN dài có điện trở không đáng kể. a) Ampe kế chỉ bao nhiêu khi MN đứng yên? Tính độ lớn lực từ tác dụng lên thanh MN khi đó. |
|
|
b) Ampe kế chỉ bao nhiêu khi MN di chuyển về phía phải với vận tốc v = 3 m/s sao cho 2 đầu MN luôn tiếp xúc với 2 thanh đỡ bằng kim loại? Tính độ lớn lực từ tác dụng lên thanh MN khi đó. c) Muốn Ampe kế chỉ số 0 phải để thanh MN di chuyển về phía nào với vận tốc là bao nhiêu? |
|
Lời giải chi tiết:
a) Khi thanh MN đứng yên thì trong mạch không có dòng cảm ứng nên số chỉ ampe kế là:
$I=\frac{E}{R+r}=0,5A$
Độ lớn lực từ tác dụng lên thanh MN: $F=B.I.\ell =0,05N$ .
b) Khi thanh chuyển động về phía phải thì trong mạch có dòng cảm ứng có chiều từ M đến N:
${{i}_{c}}=\frac{{{e}_{c}}}{R+r}=\frac{B\ell v}{R+r}=0,1A$ .
Trong mạch có 2 dòng điện là dòng do nguồn tạo ra và dòng cảm ứng do hiện tượng cảm ứng điện từ tạo ra. Hai dòng điện này cùng chiều nên số chỉ của ampe kế chính là tổng của 2 dòng này: ${{I}_{A}}=I+{{i}_{c}}=0,6A$
Lực từ tác dụng lên thanh MN khi này là: $F=B.{{I}_{A}}.\ell =0,06N$ .
c) Muốn ampe kế chỉ số 0 thì ${{i}_{c}}$ phải có độ lớn bằng I = 0,5A và dòng ${{i}_{c}}$ phải ngược chiều với dòng I, tức dòng ${{i}_{c}}$ có chiều từ N đến M $\to $ thanh MN phải chuyển động sang trái.
Gọi v là vận tốc của thanh MN: ${{i}_{c}}=\frac{B\ell v}{R+r}\Rightarrow v=\frac{{{i}_{c}}\left( R+r \right)}{B\ell }=15{m}/{s}\;$ .
|
Bài tập 4: Hai thanh kim loại song song, thẳng đứng có điện trở không đáng kể, một đầu nối vào điện trở $R=0,5\Omega $ . Một đoạn dây dẫn AB, độ dài $\ell =14cm$ , khối lượng m = 2g, điện trở $r=0,5\Omega $ tì vào hai thanh kim loại tự do trượt không ma sát xuống dưới và luôn luôn vuông góc với hai thanh kim loại đó. Toàn bộ hệ thống đạt trong một từ trường đều có hướng vuông góc với mặt phẳng hai thanh kim loại có cảm ứng từ B = 0,2T. Lấy $g=9,8{{{m}/{s}\;}^{2}}$ . |
|
|
a) Xác định chiều dòng điện qua R. b) Chứng minh rằng lúc đầu thanh AB chuy |
|