BÀI TẬP TÌM CHU KÌ, TẦN SỐ CON LẮC ĐƠN CÓ LỜI GIẢI CHI TIẾT
| Bài tập 1: [Trích đề thi đại học năm 2013]. Một con lắc đơn có chiều dài 121 cm dao động điều hòa tại nơi có gia tốc trọng trường g. Lấy ${{\pi }^{2}}=10$. Chu kì dao động của con lắc là
A. 0,5 s. B. 2 s. C. 1 s. D. 2,2 s. |
Lời giải chi tiết
Ta có: $T=2\pi \sqrt{\frac{\ell }{g}}=2\sqrt{10}.\sqrt{\frac{1,21}{10}}=2,2s.$ Chọn D.
| Bài tập 2: [Trích đề thi đại học năm 2009]. Tại nơi có gia tốc trọng trường g = 9,8 m/s, một con lắc đơn và một con lắc lò xo nằm ngang dao động điều hòa với cùng tần số. Biết con lắc đơn có chiều dài 49 cm và lò xo có độ cứng 10 N/m. Khối lượng vật nhỏ của con lắc lò xo là
A. 0,125 kg. B. 0,500 kg. C. 0,750 kg. D. 0,250 kg. |
Lời giải chi tiết
Ta có: ${{\omega }_{1}}=\sqrt{\frac{k}{m}};{{\omega }_{2}}=\sqrt{\frac{g}{\ell }}$. Khi đó ${{\omega }_{1}}={{\omega }_{2}}\Rightarrow \frac{k}{m}=\frac{g}{\ell }\Rightarrow m=0,5kg.$ Chọn B.
| Bài tập 3: Một con lắc đơn có chiều dài $\ell =64cm$ dao động điều hòa tại một nơi có gia tốc trọng trường là $g={{\pi }^{2}}{m}/{{{s}^{2}}}\;$. Con lắc thực hiện được bao nhiêu dao động trong thời gian là 12 phút.
A. 250. B. 400. C. 500. D. 450. |
Lời giải chi tiết
Ta có: $T=2\pi \sqrt{\frac{\ell }{g}}=2\pi \sqrt{\frac{0,64}{{{\pi }^{2}}}}=1,6s.$
Trong thời gian 3 phút vật thực hiện được số dao động là $N=\frac{\vartriangle t}{T}=\frac{12.60}{1,6}=450$ dao động. Chọn D.
| Bài tập 4: Một con lắc đơn có chiều dài $\ell $ dao động điều hòa với chu kì T tại nơi có gia tốc trọng trường là g. Con lắc đơn có chiều dài $\frac{\ell }{2}$ dao động điều hòa tại nơi có gia tốc trọng trường ${g}’=0,72g$ với chu kì ${T}’$ là
A. ${T}’=0,6T.$ B. ${T}’=\frac{5}{6}T.$ C. ${T}’=\frac{2}{3}T.$ D. ${T}’=1,2T.$ |
Lời giải chi tiết
Ta có: $T=2\pi \sqrt{\frac{\ell }{g}}$. Khi $\ell ‘=\frac{1}{2}\ell $ và ${g}’=0,72g\Rightarrow {T}’=2\pi \sqrt{\frac{\frac{1}{2}\ell }{0,72g}}=\sqrt{\frac{0,5}{0,72}}T.$
Do đó ${T}’=\frac{5T}{6}.$Chọn B.
| Bài tập 5: Một con lắc đơn có chu kì T = 0,77 s. Nếu thay đổi chiều dài một lượng là 24 cm thì chu kì của con lắc là ${T}’=1,155s$. Gia tốc trọng trường tại nơi làm thí nghiệm trên là
A. $g=9,89{m}/{{{s}^{2}}}\;.$ B. $g=9,62{m}/{{{s}^{2}}}\;.$ C. $g=9,84{m}/{{{s}^{2}}}\;.$ D. $g=9,9{m}/{{{s}^{2}}}\;.$ |
Lời giải chi tiết
Ta có: $T=2\pi \sqrt{\frac{\ell }{g}}=1,5\left( s \right).$
Khi thay đổi chiều dài con lắc ta có: ${T}’=2\pi \sqrt{\frac{\ell \pm 0,24}{g}}$
Suy ra $\frac{T}{{{T}’}}=\sqrt{\frac{l}{l\pm 0,24}}=\frac{2}{3}\Rightarrow \sqrt{\frac{\ell }{\ell +0,24}}=\frac{2}{3}\Leftrightarrow 1+\frac{0,24}{l}=\frac{9}{4}\Rightarrow \ell =0,192m.$
Do đó $g=\frac{4{{\pi }^{2}}\ell }{T}=9,84{m}/{{{s}^{2}}}\;.$Chọn C.
| Bài tập 6: Tại cùng một nơi trên mặt đất, một con lắc có chiều dài lần lượt là $\ell +10\left( cm \right)$,$\ell \left( cm \right)$ và $\ell -10\left( cm \right)$ thì con lắc dao động điều hòa với chu kì lần lượt là 3, $2\sqrt{2}$ và T. Giá trị của T là
A. T = 7,48 s. B. T = 1,63 s. C. T = 2,00 s. D. T = 2,65 s. |
Lời giải chi tiết
Ta có: $\frac{{{T}_{1}}}{{{T}_{2}}}=\sqrt{\frac{\ell +10}{\ell }}=\frac{3}{2\sqrt{2}}\Rightarrow 1+\frac{10}{\ell }=\frac{9}{8}\Rightarrow \ell =80cm.$
Lại có: $\frac{{{T}_{2}}}{{{T}_{1}}}=\sqrt{\frac{\ell }{\ell -10}}=\frac{2\sqrt{2}}{T}=\sqrt{\frac{80}{70}}\Rightarrow T=2,65s.$Chọn D.
| Bài tập 7 [Trích đề thi đại học năm 2009]: Tại một nơi trên mặt đất, một con lắc đơn dao động điều hòa. Trong khoảng thời gian $\vartriangle t$, con lắc thực hiện 60 dao động toàn phần; thay đổi chiều dài con lắc một đoạn 44 cm thì cũng trong khoảng thời gian $\vartriangle t$ ấy, nó thực hiện 50 dao động toàn phần. Chiều dài ban đầu của con lắc là
A.80 cm. B.100 cm. C. 60 cm. D. 144 cm. |
Lời giải chi tiết
Gọi chiều dài ban đầu của con lắc là $\ell $
Khi đó: $T=\frac{\vartriangle t}{60}=2\pi \sqrt{\frac{\ell }{g}}$, khi thay điỉu chiều dài con lắc ${T}’=\frac{\vartriangle t}{50}=2\pi \sqrt{\frac{\ell \pm 0,44}{g}}$
Ta có: $\frac{T}{{{T}’}}=\frac{5}{6}=\sqrt{\frac{\ell }{\ell \pm 0,44}}\Rightarrow \frac{5}{6}=\sqrt{\frac{\ell }{\ell +0,24}}\Leftrightarrow \frac{36}{25}=1+\frac{0,44}{\ell }\Rightarrow \ell =1m=100cm.$ Chọn B.
| Bài tập 8: Một con lắc đơn khi dao động trên mặt đất, chu kì dao động 2,4 s. Đem con lắc lên Mặt Trăng mà không thay đổi chiều dài thì chu kỳ dao động của nó là bao nhiêu? Biết rằng khối lượng Trái Đất gấp 81 lần khối lượng Mặt Trăng, bán kính Trái Đất bằng 3,7 lần bán kính Mặt Trăng.
A. 5,8 s. B. 4,8 s. C. 3,8 s. D. 2,8 s. |
Lời giải chi tiết
$\frac{{{T}’}}{T}=\frac{2\pi \sqrt{\frac{l}{{{g}’}}}}{2\pi \sqrt{\frac{l}{g}}}=\sqrt{\frac{g}{{{g}’}}}=\sqrt{\frac{\frac{GM}{{{R}^{2}}}}{\frac{G{M}’}{{{{{R}’}}^{2}}}}
}=\sqrt{\frac{M}{{{M}’}}}.\frac{{{R}’}}{R}=9.\frac{1}{3,7}\Leftrightarrow {T}’=5,8\left( s \right).$Chọn A.
| Bài tập 9: Một con lắc đơn có chiều dài ${{\ell }_{1}}$ dao động điều hòa với chu kì ${{T}_{1}}=2s$, con lắc đơn có chiều dài ${{\ell }_{2}}$ dao động điều hòa với chu kì ${{T}_{2}}=1,2s$. Tính chu kì dao động của con lắc có chiều dài là $\ell =3{{\ell }_{1}}+{{\ell }_{2}}.$
A. T = 3,67 s. B. T = 3,63 s. C. T = 3,25 s. D. T = 2,33 s. |
Lời giải chi tiết
Ta có: ${{T}_{1}}=2\pi \sqrt{\frac{{{\ell }_{1}}}{g}};{{T}_{2}}=2\pi \sqrt{\frac{{{\ell }_{2}}}{g}}.$
Khi đó $T=2\pi \sqrt{\frac{3{{\ell }_{1}}+{{\ell }_{2}}}{g}}\Rightarrow {{T}^{2}}=3{{T}_{1}}^{2}+{{T}_{2}}^{2}\Rightarrow T=3,666s.$Chọn A.
Bài tập 10: Trong cùng một khoảng thời gian $\vartriangle t$ con lắc có chiều dài ${{\ell }_{1}}$ thực hiện được 60 dao động, con lắc có chiều dài ${{\ell }_{2}}$ thực hiện được 75 dao động, biết hiệu chiều dài hai con lắc bằng. Tìm chiều dài ${{\ell }_{1}}$.
|
Lời giải chi tiết
Gọi chu kì con lắc có chiều dài ${{\ell }_{1}},{{\ell }_{2}}$ lần lượt là ${{T}_{1}},{{T}_{2}}.$
Khi đó ta có: ${{T}_{1}}=2\pi \sqrt{\frac{{{\ell }_{1}}}{g}};{{T}_{2}}=2\pi \sqrt{\frac{{{\ell }_{2}}}{g}}.$
Mặt khác: $\frac{\vartriangle t}{{{N}_{1}}} {} :\frac{\vartriangle t}{{{N}_{2}}}=\frac{{{T}_{1}}}{{{T}_{2}}}=\sqrt{\frac{{{\ell }_{1}}}{{{\ell }_{2}}}}\Leftrightarrow {{\left( \frac{75}{60} \right)}^{2}}=\frac{{{\ell }_{1}}}{{{\ell }_{2}}}=\frac{25}{16}.$
Lại có: ${{\ell }_{1}}-{{\ell }_{2}}=36cm\Rightarrow \frac{25}{16}{{\ell }_{2}}-{{\ell }_{2}}=36\Rightarrow \left\{ \begin{array}{} {{\ell }_{2}}=64cm \\ {} {{\ell }_{1}}=100cm \\ \end{array} \right..$ Chọn A
| Bài tập 11: Để chu kì con lắc đơn tăng thêm 5% thì phải tăng chiều dài của nó thêm
A. 2,25%. B. 5,75%. C. 10,25%. D. 25%. |
Lời giải chi tiết
Ta có:
$\begin{array}{} {T}’=T+5%T=1,05T \\ {} \Rightarrow \ell ‘=1,{{05}^{2}}.\ell =1,1025.\ell =110,25%\ell ; \\ \end{array}$
$\Rightarrow $ Chiều dài con lắc đơn cần tăng thêm 10,25%. Chọn C.
| Bài tập 12: Một con lắc đơn có độ dài 120 cm. Để chu kỳ dao động mới chỉ bằng 90% chu kỳ dao động ban đầu thì phải điều chỉnh độ dài dây treo của con lắc thành
A. 148 cm. B. 133 cm. C. 108 cm. D. 97,2 cm. |
Lời giải chi tiết
${T}’=0,9T\Rightarrow \ell ‘=0,{{9}^{2}}.\ell =0,{{9}^{2}}.120=97,2cm.$ Chọn D.
| Bài tập 13: Xét trường hợp con lắc đơn lý tưởng đang dao động điều hòa tại một vị trí xác định trong trường trọng lực. Khi dây treo có độ dài $({{\ell }_{1}}+{{\ell }_{2}})$ thì chu kỳ dao động điều hòa của con lắc bằng 4 s. Khi dây treo có độ dài $({{\ell }_{1}}-{{\ell }_{2}})$ thì chu kì dao động của con lắc bằng 2 s. Chu kỳ dao động của con lắc trong 2 trường hợp, khi dây treo có độ dài ${{\ell }_{1}}$ và khi dây treo có độ dài ${{\ell }_{2}}$ tương ứng bằng
A. $\sqrt{10}s,\sqrt{3}s.$ B. $\sqrt{5}s,2\sqrt{3}s.$ C. $\sqrt{10}s,\sqrt{6}s.$ D. $\sqrt{5}s,\sqrt{3}s.$ |
Lời giải chi tiết
${{T}^{2}}$ tỉ lệ thuận với $\ell $ do đó
Nếu $\ell ={{\ell }_{1}}+{{\ell }_{2}}\Rightarrow {{T}_{+}}^{2}={{T}_{1}}^{2}+{{T}_{2}}^{2}$
Nếu $\ell ={{\ell }_{1}}-{{\ell }_{2}}\Rightarrow {{T}_{-}}^{2}={{T}_{1}}^{2}-{{T}_{2}}^{2}.$
Thay số vào được hệ phương trình: $\left\{ \begin{array}{} {{T}_{1}}^{2}+{{T}_{2}}^{2}=4 \\ {} {{T}_{1}}^{2}-{{T}_{2}}^{2}=2 \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{} {{T}_{1}}=\sqrt{10}s \\ {} {{T}_{2}}=\sqrt{6}s \\ \end{array} \right..$ Chọn C.
| Bài tập 14: [Trích đề thi thử THPT QG chuyên Lương Văn Chánh – Phú Yên]. Một con lắc đơn có chu kỳ dao động điều hòa là T. Khi giảm chiều dài con lắc 10 cm thì chu kỳ dao động của con lắc biến thiên 0,1s. Chu kỳ dao động T ban đầu của con lắc là
A. T = 1,9 s. B. T = 1,95 s. C. T = 2,05 s. D. T = 2 s. |
Lời giải chi tiết
Ta có:
$\begin{array}{} 2\pi \sqrt{\frac{\ell }{g}}-2\pi \sqrt{\frac{\ell -0,1}{g}}=0,1\Rightarrow \sqrt{\ell }-\sqrt{\ell -0,1}=\frac{0,1}{2\pi }\sqrt{g}=0,05 \\ {} \Rightarrow \ell =1,05\Rightarrow T=2,05s. \\ \end{array}$
Chọn C.
| Bài tập 15: [Trích đề thi đại học năm 2013]. Hai con lắc đơn có chiều dài lần lượt là 82 cm và 64 cm được treo ở trần một căn phòng. Khi các vật nhỏ của hai con lắc đang ở vị trí cân bằng, đồng thời truyền cho chúng các vận tốc cùng hướng sao cho hai con lắc dao động điều hòa với cùng biên độ góc, trong hai mặt phẳng song song với nhau. Gọi $\vartriangle t$ là khoảng thời gian ngắn nhất kể từ lúc truyền vận tốc đến lúc hai dây treo song song nhau. Giá trị $\vartriangle t$ gần giá trị nào nhất sau đây?
A. 2,36 s. B. 8,12 s. C. 0,45 s. D. 7,20 s. |
Lời giải chi tiết
Phương trình dao động của 2 con lắc lần lượt là ${{x}_{1}}=A\cos \left( {{\omega }_{1}}t-\frac{\pi }{2} \right)$ và ${{x}_{2}}=A\cos \left( {{\omega }_{2}}t-\frac{\pi }{2} \right).$
Trong đó ${{\omega }_{1}}=\sqrt{\frac{g}{{{\ell }_{1}}}}=\sqrt{\frac{10}{0,81}};{{\omega }_{2}}=\sqrt{\frac{g}{{{\ell }_{2}}}}=\sqrt{\frac{10}{0,64}}.$
Hai con lắc gặp nhau khi ${{x}_{1}}={{x}_{2}}\Leftrightarrow \left[ \begin{array}{} {{\omega }_{1}}t={{\omega }_{2}}t+k2\pi \\ {} {{\omega }_{1}}t-\frac{\pi }{2}=-\left( {{\omega }_{2}}t-\frac{\pi }{2} \right)+k2\pi \\ \end{array} \right..$
$\Leftrightarrow \left[ \begin{array}{} t=\frac{k2\pi }{\left| {{\omega }_{1}}-{{\omega }_{2}} \right|} \\ {} t=\frac{\pi +k2\pi }{{{\omega }_{1}}+{{\omega }_{2}}} \\ \end{array} \right.\Rightarrow \vartriangle {{t}_{\min }}=\frac{\pi }{{{\omega }_{1}}+{{\omega }_{2}}}=0,42\left( s \right).$(chọn $k={{k}_{\min }}$).
Các em có thể hiểu tại thời điểm đầu tiên 2 con lắc có cùng li độ, chúng đi ngược chiều nhau.
Chọn C.
| Bài tập 16: [Trích đề thi chuyên Vinh lần 1 – năm 2017]. Một con lắc lò xo chiều dài tự nhiên treo ${{\ell }_{0}}$ thẳng đứng, vật treo khối lượng ${{m}_{0}}$ treo gần một con lắc đơn chiều dài dây treo $\ell $ khối lượng vật treo m. Với con lắc lò xo, tại vị trí cân bằng lò xo giãn $\vartriangle {{\ell }_{0}}$. Để hai con lắc có chu kỳ dao động điều hòa như nhau thì
A. $\ell =2\vartriangle {{\ell }_{0}}.$ B. $\ell ={{\ell }_{0}}.$ C. $\ell =\vartriangle {{\ell }_{0}}.$ D. $m={{m}_{0}}.$ |
Lời giải chi tiết
Ta có: Chu kì con lắc đơn: $T=2\pi \sqrt{\frac{\ell }{g}}$, chu kì con lắc lò xo: ${T}’=2\pi \sqrt{\frac{\vartriangle \ell }{g}}.$
Để $T={T}’$ thì $\ell =\vartriangle {{\ell }_{0}}.$ Chọn C.
Bài tập 17: Một con lắc đơn khi dao động trên mặt đất tại nơi có gia tốc trọng trường $9,819{m}/{{{s}^{2}}}\;$, chu kỳ dao động 2 (s). Đưa con lắc đơn đến nơi khác có gia tốc trọng trường $9,793{m}/{{{s}^{2}}}\;$. Muốn chu kỳ không đổi, phải thay đổi chiều dài của con lắc như thế nào?
|
Lời giải chi tiết
$\frac{{{T}’}}{T}=\frac{2\pi \sqrt{\frac{\ell ‘}{{{g}’}}}}{2\pi \sqrt{\frac{\ell }{g}}}=\sqrt{\frac{\ell ‘}{\ell }}.\sqrt{\frac{g}{{{g}’}}}\Leftrightarrow \frac{\ell ‘}{\ell }=\frac{{{g}’}}{g}=\frac{9,793}{9,819}=0,997=100%-0,3%.$ Chọn A
| Bài tập 18: Cho con lắc đơn lý tưởng gồm dây treo độ dài 40 cm treo tại vị trí có gia tốc trọng trường bằng $10{m}/{{{s}^{2}}}\;$. Kích thích để con lắc dao động điều hòa với góc quét của dây treo bằng ${{10}^{\circ }}$. Gia tốc cực đại của quả nặng trong quá trình dao động bằng
A. ${35,24cm}/{{{s}^{2}}}\;.$ B. ${53,42cm}/{{{s}^{2}}}\;.$ C. ${87,27cm}/{{{s}^{2}}}\;.$ D. ${78,72cm}/{{{s}^{2}}}\;.$ |
Lời giải chi tiết
Góc quét bằng ${{10}^{\circ }}\Rightarrow $biên độ góc ${{\alpha }_{0}}=\frac{{{10}^{\circ }}}{2}={{5}^{\circ }}=\frac{5\pi }{180}=0,0873rad;$
Biên độ dài $A={{\alpha }_{0}}\ell =0,0873.40=3,491cm.$
Tần số góc $\omega =\sqrt{\frac{g}{\ell }}=\sqrt{\frac{10}{0,4}}=5{rad}/{s}\;.$
Gia tốc cực đại ${{a}_{\max }}={{\omega }^{2}}A={{5}^{2}}.3,491=87,27{cm}/{{{s}^{2}}.}\;$ Chọn C.
| Bài tập 19: Cho con lắc đơn lý tưởng đang dao động điều hòa tại vị trí có gia tốc trọng trường bằng $10{m}/{{{s}^{2}}}\;$ với phương trình ly độ góc $\alpha =0,05.cos\left( 2\pi t+{\pi }/{3}\; \right)rad.$ Lấy gần đúng ${{\pi }^{2}}=10$. Tổng quãng đường đi được của quả nặng sau 5 s chuyển động là
A. 25 cm. B. 50 cm. C. 5 cm. D. 10 cm. |
Lời giải chi tiết
Phương trình ly độ góc $\alpha =0,05.cos\left( 2\pi t+{\pi }/{3}\; \right)rad\Rightarrow $ biên độ góc ${{\alpha }_{0}}=0,05rad;$
Tần số góc $\omega =\sqrt{\frac{g}{\ell }}\Rightarrow \ell =\frac{g}{{{\omega }^{2}}}=\frac{10}{4{{\pi }^{2}}}=0,25m=25cm.$
Biên độ dài $A=\ell .{{\alpha }_{0}}=25.0,05=1,25cm.$
Chu kì $T=\frac{2\pi }{\omega }=\frac{2\pi }{2\pi }=1s.$ Một vật T đi được quãng đường bằng 4A
$\Rightarrow $Quãng đường đi được trong $t=5s=5T$ là $S=5.4A=5.4.1,25=25cm.$ Chọn A.
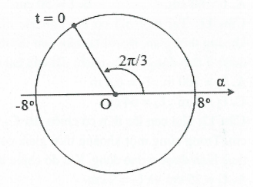
| Bài tập 20: Một con lắc đơn gồm dây treo có độ dài 25 cm và một vật nhỏ, treo tại nơi có gia tốc trọng trường bằng $10{m}/{{{s}^{2}}}\;$. Lấy gần đúng ${{\pi }^{2}}=10$. Đưa vật theo chiều dương tới vị trí dây treo lệch với phương thẳng đứng một góc bằng ${{8}^{\circ }}$ rồi buông nhẹ. Thời điểm ban đầu, t = 0 được chọn sau thời điểm vật bắt đầu chuyển động 1/3 s. Phương trình ly độ góc của chất điểm là
A. $\alpha ={{4}^{\circ }}\cos \left( 2\pi t+{2\pi }/{3}\; \right).$ B. $\alpha ={{8}^{\circ }}\cos \left( 2\pi t+{\pi }/{2}\; \right).$ C. $\alpha ={{8}^{\circ }}\cos \left( 2\pi t-{2\pi }/{3}\; \right).$ D. $\alpha ={{8}^{\circ }}\cos \left( 2\pi t+{2\pi }/{3}\; \right).$ |
Lời giải chi tiết
| Kéo con lắc ra ${{8}^{\circ }}$, rồi buông $\Rightarrow $trong quá trình dao động con lắc lệch góc lớn nhất bằng ${{8}^{\circ }}\Rightarrow {{\alpha }_{0}}={{8}^{\circ }}.$
$\omega =\sqrt{\frac{g}{\ell }}=\sqrt{\frac{10}{0,25}}=\sqrt{40}=2\pi {rad}/{s}\;.$ Ban đầu kéo ra ${{8}^{\circ }}$ theo chiều dương $\Rightarrow $ Vật ở biên dương. Sau một khoảng thời gian 1/3s, M quay được một góc ${{\vartriangle }_{\varphi }}=\omega t={2\pi }/{3,}\;$ lúc này tính thời gian dao động (t = 0) nên $\varphi ={2\pi }/{3}\;.$ $\Rightarrow $ Phương trình: $\alpha ={{8}^{\circ }}\cos \left( 2\pi t+{2\pi }/{3}\; \right).$ Chọn D.
|
 |
