LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
1. Con lắc đơn
|
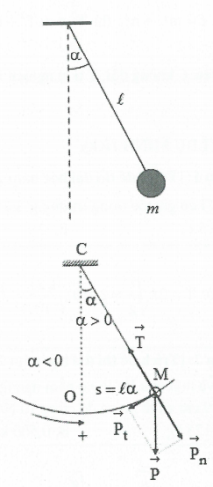
§ Cấu tạo: Con lắc đơn gồm một vật nhỏ, khối lượng m, treo ở đầu của một sợi dây không giãn, có chiều dài $\ell $ (hình bên). Vị trí cân bằng của con lắc: Là vị trí dây treo có phương thẳng đứng. Con lắc sẽ đứng yên mãi ở vị trí này nếu lúc đầu nó đứng yên. Kéo nhẹ quả cầu cho dây treo lệch khỏi vị trí cân bằng một góc $\alpha $ rồi thả ra, ta thấy con lắc dao động quanh vị trí cân bằng trong mặt phẳng thẳng đứng đi qua điểm treo và vị trí ban đầu của vật. § Phương trình động lực học: Chọn chiều dương từ trái sang phải, gốc tọa độ cong tại vị trí cân bằng O. Khi ấy vị trí của vật m được xác định bởi li độ góc $\alpha =\widehat{OCM}$ hay bởi li độ cong (dài) $s=\overset\frown{OM}=\ell \alpha $. Trong khi dao động vật chịu tác dụng của trọng lực $\overrightarrow{P}$ và lực căng $\overrightarrow{T}$. Ta phân tích trọng lực $\overrightarrow{P}$ thành 2 phần như hình vẽ: $\overrightarrow{P}=\overrightarrow{{{P}_{t}}}+\overrightarrow{{{P}_{n}}}$ Lực thành phần $\overrightarrow{{{P}_{n}}}$ theo hướng vuông góc với quỹ đạo Lực thành phần $\overrightarrow{{{P}_{t}}}$ theo hướng tiếp tuyến với quỹ đạo. +) Lực căng $\overrightarrow{T}$ và lực thành phần $\overrightarrow{{{P}_{n}}}$ vuông góc với đường đi nên không làm thay đổi tốc độ của vật. Hợp lực của chúng là lực hướng tâm giữ cho vật chuyển động trên cung tròn. |
|
+) Lực thành phần $\overrightarrow{{{P}_{t}}}$ là lực kéo về và có giá trị đại số ${{P}_{t}}=-mg\sin \alpha $.
Công thức trên cho thấy dao động của con lắc đơn nói chung không phải dao động điều hòa.
Nếu $\alpha $ nhỏ thì $\sin \alpha \approx \alpha \left( rad \right)$. Khi đó ta có: ${{P}_{t}}=-mg\alpha =-mg.\frac{s}{\ell }$.
Như vậy, khi dao động nhỏ $\left( \sin \alpha \approx \alpha \left( rad \right) \right)$(bỏ qua ma sát) thì con lắc đơn dao động điều hòa với phương trình $s={{s}_{0}}\cos \left( \omega t+\varphi \right)$ với tần số góc $\omega =\sqrt{\frac{g}{\ell }}$, biên độ dao động là ${{s}_{o}}=\ell .{{\alpha }_{o}}$.
2. Chu kì, tần số của con lắc đơn.
– Tần số góc $\omega =\sqrt{\frac{g}{\ell }}$, chu kì $T=2\pi \sqrt{\frac{\ell }{g}}$, tần số dao động $f=\frac{1}{2\pi }\sqrt{\frac{g}{\ell }}$
Có $\omega $, T, f không phụ thuộc vào khối lượng m của vật nặng, không phụ thuộc vào cách kích thích dao động.
– Thay đổi chiều dài của con lắc đơn.
Ta có: ${{T}_{1}}=2\pi \sqrt{\frac{{{\ell }_{1}}}{g}};{{T}_{2}}=2\pi \sqrt{\frac{{{\ell }_{2}}}{g}}.$
+) Nếu g không đổi, T tỉ lệ thuận với $\sqrt{\ell }$ hay ${{T}^{2}}$ tỉ lệ thuận với $\ell $.
Nếu $\ell ={{\ell }_{1}}+{{\ell }_{2}}$ thì${{T}^{2}}={{T}_{1}}^{2}+{{T}_{2}}^{2};\frac{1}{{{f}^{2}}}=\frac{1}{{{f}_{1}}^{2}}+\frac{1}{{{f}_{2}}^{2}}.$
Tổng quá: nếu $\ell ={{\ell }_{1}}+{{\ell }_{2}}+..+{{\ell }_{n}}$ thì ${{T}^{2}}={{T}_{1}}^{2}+{{T}_{2}}^{2}+{{T}_{3}}^{2}+…+{{T}_{n}}^{2}.$
Nếu $\ell =m{{\ell }_{1}}+n{{\ell }_{2}}$ thì ${{T}^{2}}=m{{T}_{1}}^{2}+n{{T}_{2}}^{2};\frac{1}{{{f}^{2}}}=m\frac{1}{{{f}_{1}}^{2}}+n\frac{1}{{{f}_{2}}^{2}}.$
+) Nếu $\ell $ không đổi, T tỉ lệ nghịch với $\sqrt{g}\Rightarrow \frac{{{T}_{1}}}{{{T}_{2}}}=\sqrt{\frac{{{g}_{2}}}{{{g}_{1}}}}=\frac{{{f}_{2}}}{{{f}_{1}}}.$