CÁCH GIẢI CÁC DẠNG TOÁN LIÊN QUAN ĐẾN LỰC VÀ THỜI GIAN DÃN NÉN
1. ĐẶT VẤN ĐỀ
Dạng toán: Bài toán liên quan đến tính thời gian lò xo nén hay dãn trong một chu kỳ khi vật treo ở dưới và $A>\Delta {{\ell }_{0}}$.
2. PHƯƠNG PHÁP GIẢI
Chuyển về bài toán quen thuộc là tìm thời gian vật đi từ li độ ${{x}_{1}}$ đến ${{x}_{1}}$.
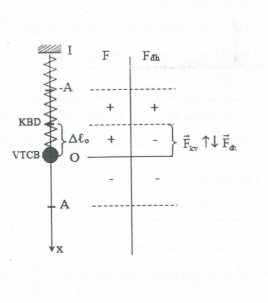
– Khoảng thời gian lò xo nén là: $\Delta t=\frac{2\alpha }{\omega }=2.\frac{1}{\omega }.\operatorname{arcos}\frac{\Delta {{\ell }_{0}}}{A}$.
– Khoảng thời gian lò xo dãn là: $T-\Delta t$.
Chú ý:
+) Lực đàn hồi có chiều luôn hướng về vị trí lò xo không biến dạng. Tại đó, lực đàn hồi đổi chiều, lò xo chuyển từ dãn sang nén hoặc ngược lại.
+) Lực kéo về ( lực phục hồi ) luôn hướng về vị trí cân bằng. Tại đó, lực kéo về đổi chiều.
Do vậy, có những khoảng trên quĩ đạo dao động, lực đàn hồi và lực phục hồi cùng hoặc ngược chiều nhau. Đoạn ngược chiều từ vị trí cân bằng đến vị trí không biến dạng theo chiều âm và theo chiều dương.
