LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
1. Vecto quay
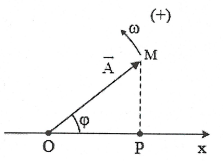
| Ta có phương trình $x=A\cos \left( \omega +\varphi \right)$ là phương trình của hình chiếu của vecto quay $\overline{OM}$ lên trục x. Dựa vào dao động điều hòa người ta đưa ra cách biểu diễn phương trình của dao động điều hòa bằng một vecto quay được vẽ tại thời điểm ban đầu. Vecto quay có đặc điểm:
+) Có gốc tại gốc tọa độ của trục Ox. +) Có độ dài bằng biên độ dao động OM = A. +) Hợp với trục Ox một góc bằng pha ban đầu (chọn chiều dương là chiều dương của đường tròn lượng giác). |
|
2. Phương pháp giản đồ Fre-nen
Giả sử ta cần tổng hợp của hai dạo động điều hòa cùng phương, cùng tần số sau:
${{x}_{1}}={{A}_{1}}\cos \left( \omega t+{{\varphi }_{1}} \right)$ và $x{{ {} }_{2}}={{A}_{2}}\cos \left( \omega t+{{\varphi }_{2}} \right)$ .
l Trong trường hợp ${{A}_{1}}={{A}_{2}}=A$ ta dùng công thức lượng giác:
$\cos a+\cos b=2\cos \frac{a+b}{2}\cos \frac{a-b}{2}$ ta được: ${{x}_{1}}+{{x}_{2}}=2A\cos \left( \omega t+\frac{{{\varphi }_{1}}+{{\varphi }_{2}}}{2} \right)\cos \left( \frac{{{\varphi }_{1}}-{{\varphi }_{2}}}{2} \right)$ .
l Trong trường hợp ${{A}_{1}}\ne {{A}_{2}}$ ta có thẻ dùng phương pháp Fre-nen như sau:
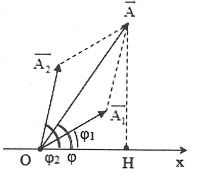
| +) Vẽ lần lượt hai vecto quay $\overrightarrow{{{A}_{1}}}$ và $\overrightarrow{{{A}_{2}}}$ biểu diễn hai li độ ${{x}_{1}}={{A}_{1}}\cos \left( \omega t+{{\varphi }_{1}} \right)$ và ${{x}_{2}}={{A}_{2}}\cos \left( \omega t+{{\varphi }_{2}} \right)$ tại thời điểm ban đầu.
+) Sau đó vẽ vecto $\overrightarrow{A}=\overrightarrow{{{A}_{1}}}+\overrightarrow{{{A}_{2}}}$ theo quy tắc hình bình hành. Khi đó vecto chéo $\overrightarrow{A}$ là vecto quay với tốc độ góc $\omega $ quanh gốc tọa độ O. Vì tổng các hình chiếu của hai vecto $\overrightarrow{{{A}_{1}}}$ và $\overrightarrow{{{A}_{2}}}$ lên trục Ox bằng hình chiếu của vecto $\overrightarrow{A}$ lên trục đó, nên vecto quay $\overrightarrow{A}$ biểu diễn phương trình dao động điều hòa tổng hợp là $x=A\cos \left( \omega t+\varphi \right)$ . |
 |
Vậy, dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số là một dao động điều hòa cùng phương, cùng tần số với hai dao động đó.
Trong trường hợp tổng quát, biên độ và pha ban đầu được tính bằng các công thức sau:
${{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \left( {{\varphi }_{1}}-{{\varphi }_{2}} \right)$ và $\tan \varphi =\frac{{{A}_{1}}\sin {{\varphi }_{1}}+{{A}_{2}}\sin {{\varphi }_{2}}}{{{A}_{1}}\cos {{\varphi }_{1}}+{{A}_{2}}\cos {{\varphi }_{2}}}$ .
Từ công thức trên ta thấy rằng biên độ dao động tổng hợp phụ thuộc vào các biên độ thành phần và độ lệch pha $\Delta \varphi ={{\varphi }_{1}}-{{\varphi }_{2}}$ .
+) Nếu hai dao động cùng pha: ${{\varphi }_{1}}-{{\varphi }_{_{2}}}=k2\pi \Rightarrow A={{A}_{\max }}={{A}_{1}}+{{A}_{2}}$ .
+) Nếu hai dao động ngược pha: ${{\varphi }_{1}}-{{\varphi }_{2}}=\pi +k2\pi \Rightarrow A={{A}_{\min }}=\left| {{A}_{1}}-{{A}_{2}} \right|$ .
+) Nếu hai dao động vuông pha: ${{\varphi }_{2}}-{{\varphi }_{1}}=\frac{\pi }{2}+k\pi \Rightarrow A=\sqrt{A_{1}^{2}+A_{2}^{2}}$ .
$\Rightarrow $ Trong mọi trường hợp giá trị của A thuộc: $\left| {{A}_{1}}-{{A}_{2}} \right|\le A\le \left| {{A}_{1}}+{{A}_{2}} \right|$ .
3. Tổng hợp nhiều dao động.
Biểu diễn mỗi dao động bằng một vecto quay trong mặt phẳng Oxy, gốc tại O.
Thiết lập phương trình tổng hợp: $x={{x}_{1}}+{{x}_{2}}+..+{{x}_{n}}.$
Khi đó $\overrightarrow{A}=\overrightarrow{{{A}_{1}}}+\overrightarrow{{{A}_{2}}}+…+\overrightarrow{{{A}_{n}}}$ . Chiếu phương trình lên các trục tọa độ Ox, Oy ta có:
$\left\{ \begin{array}{} {{A}_{x}}={{A}_{1x}}+{{A}_{2x}}+….+{{A}_{n\text{x}}} \\ {} {{A}_{y}}={{A}_{1y}}+{{A}_{1y}}+….+{{A}_{ny}} \\ \end{array} \right.$ suy ra $\left\{ \begin{array}{} {{A}_{x}}={{A}_{1}}\cos {{\varphi }_{1}}+{{A}_{2}}\cos {{\varphi }_{2}}+….+{{A}_{n}}\cos {{\varphi }_{n}} \\
{} {{A}_{y}}={{A}_{1}}\sin {{\varphi }_{1}}+{{A}_{2}}\sin {{\varphi }_{2}}+….+{{A}_{n}}\sin {{\varphi }_{n}} \\ \end{array} \right.$ .
Khi đó ta có:$\left\{ \begin{array}{} A=\sqrt{A_{x}^{2}+A_{y}^{2}} \\ {} \tan \varphi =\frac{{{A}_{y}}}{{{A}_{x}}} \\ \end{array} \right.$ .
4. Tổng hợp dao động bằng máy tính CASIO
Để tổng hợp các dao động: $~~{{x}_{1}}={{A}_{1}}\cos \left( \omega t+{{\varphi }_{1}} \right);$${{x}_{2}}={{A}_{2}}\cos \left( \omega t+{{\varphi }_{2}} \right),….,{{x}_{n}}={{A}_{n}}\cos \left( \omega t+{{\varphi }_{n}} \right)$ ta viết dưới dạng số phức ${{x}_{i}}={{A}_{i}}\cos \left( \omega t+{{\varphi }_{i}} \right)\Rightarrow {{x}_{i}}={{A}_{i}}\angle {{\varphi }_{i}}$ .
Khi đó $x={{x}_{1}}+{{x}_{2}}+..{{x}_{n}}={{A}_{1}}\angle {{\varphi }_{1}}+{{A}_{2}}\angle {{\varphi }_{2}}+..+{{A}_{n}}\angle {{\varphi }_{n}}$ .
Chú ý: nếu phương trình để ở dạng sin ta phải đưa phương trình về dạng chuẩn $x=A\cos \left( \omega t+\varphi \right)$ .
| Thao tác. | Màn hình hiển thị. |
| Bước 1: Chuyển sang chế độ radian bằng thao tác
$$ (các bạn có thể để ở chế độ độ vẫn được). |
 |
| Bước 2: Nhấn $$ để chuyển sang chế độ $$ để nhân chia cộng trừ số phức.
|
 |
| Bước 3: Cộng, trừ các dao động thành phần.
${{A}_{1}}\left( – \right){{\varphi }_{1}}+{{A}_{2}}\left( – \right){{\varphi }_{2}}+….$ Sau khi được tổng các dao động ta bấm $$ để kết quả về dạng $A\angle \varphi $ . |
 |
Bài tập: Tổng hợp 2 dao động ${{x}_{1}}=5\cos \left( \omega t+\frac{\pi }{3} \right)$ và ${{x}_{2}}=5\sqrt{3}\cos \left( \omega t-\frac{\pi }{2} \right)$ ta nhập:
$\left( – \right)\frac{\pi }{3}+\left( – \right)\frac{-\pi }{2}=$
Sau đó nhấn $$ ta được kết quả là $5\angle \frac{-\pi }{3}$ .
Như vậy $x={{x}_{1}}+{{x}_{2}}=5\cos \left( \omega t-\frac{\pi }{3} \right)$ .
5. Bài toán nghịch
Nếu biết một dao động thành phần là ${{x}_{1}}={{A}_{1}}\cos \left( \omega t+{{\varphi }_{1}} \right)$ và dao động tổng hợp có phương trình là $x=A\cos \left( \omega t+\varphi \right)$ thì dao động thành phần là ${{x}_{2}}={{A}_{2}}\cos \left( \omega t+{{\varphi }_{2}} \right)$ được xác định bởi ${{x}_{2}}=x-{{x}_{1}}$ :
${{A}_{2}}\angle {{\varphi }_{2}}=A\angle \varphi -{{A}_{1}}\angle {{\varphi }_{1}}$ hoặc $\left\{ \begin{array}{} A_{2}^{2}={{A}^{2}}+A_{1}^{2}-2A{{A}_{1}}\cos \left( \varphi -{{\varphi }_{1}} \right) \\ {} \tan {{\varphi }_{2}}=\frac{{{A}_{1}}\sin \varphi -{{A}_{1}}\sin {{\varphi }_{1}}}{A\cos \varphi -{{A}_{1}}\cos {{\varphi }_{1}}} \\ \end{array} \right.$ .
6. Bài toán khoảng cách trong dao động điều hòa
Hai chất điểm dao động trên cùng trục tọa độ, chất điểm thứ nhất có phương trình
${{x}_{1}}={{A}_{1}}\cos \left( \omega t+{{\varphi }_{1}} \right)$ chất điểm thứ hai có phương trình x ![]() , hai chất điểm không va chạm nhau thì khoảng cách giữa chúng là:
, hai chất điểm không va chạm nhau thì khoảng cách giữa chúng là:
![]()
![]() , với
, với ![]() .
.
Khi đó:
+) Khoảng cách lớn nhất giữa 2 chất điểm: ![]() .
.
+) Hai chất điểm gặp nhau: ![]() .
.
7. Một số công thức toán và chú ý:
n Định lý sin: ![]()
Sử dụng hàm sin khi bài toán cho một cặp cạnh và góc đối nhau là hằng số.
n Định lý hàm cosin: ![]()
Sử dụng hàm cosin khi bài toán đã cho 2 cạnh và góc xen giữa.
n Tỉ lệ thức: ![]() .
.
n Li độ tổng hợp bằng tổng các li độ thành phần: ![]()
n Véc-tơ tổng hợp luôn nằm giữa 2 véc-tơ thành phần, tức nó nhanh pha hơn một dao động thành phần và chậm pha hơn dao động thành phần còn lại.