LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
1. Độ lệch pha giữa 2 điểm ở cùng một thời gian
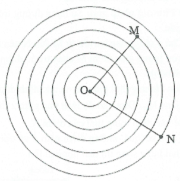
Xét 2 điểm M,N cách nguồn một khoảng ${{x}_{1}},{{x}_{2}}.$
Phương trình sóng tại M là ${{u}_{M}}=A\cos \left( \omega t-\frac{2\pi {{x}_{1}}}{\lambda } \right).$
Phương trình sóng tại N là ${{u}_{N}}=A\cos \left( \omega t-\frac{2\pi {{x}_{2}}}{\lambda } \right).$
Độ lệch pha dao động của M và N tại cùng một thời điểm là $\Delta \varphi =\frac{2\pi \left( {{x}_{2}}-{{x}_{1}} \right)}{\lambda }.$
Nếu 2 điểm M và N cùng nằm trên một phương truyền song cách nhau một khoảng d thì ta có:$d={{x}_{2}}-{{x}_{1}}$
Độ lệch pha giữa 2 dao động tại M và N là$\Delta \varphi =\frac{2\pi d}{\lambda }.$
Như vậy: Xét trên cùng một phương truyền sóng.
+) Hai điểm M và N cùng pha với nhau khi: $\Delta \varphi =\frac{2\pi d}{\lambda }=k2\pi \Leftrightarrow d=k\lambda .$
M, N gần nhau nhất khi $MN=\lambda .$
+) Hai điểm M và N ngược pha với nhau khi: $\Delta \varphi =\frac{2\pi d}{\lambda }=\left( 2k+1 \right)\pi \Leftrightarrow d=\left( k+0,5 \right)\lambda .$
M, N gần nhau nhất khi $MN=\frac{\lambda }{2}.$
+) Hai điểm M và N vuông pha với nhau khi: $\Delta \varphi =\frac{2\pi d}{\lambda }=\left( k+\frac{1}{2} \right)\pi \Leftrightarrow d=\left( 2k+1 \right)\frac{\lambda }{4}.$
M, N gần nhau nhất khi$MN=\frac{\lambda }{4}.$
2. Độ lệch pha của một điểm ở hai thời điểm khác nhau
Xét 2 điểm M cách nguồn một khoảng x.
Phương trình sóng tại M là ${{u}_{M}}=A\cos \left( \omega t-\frac{2\pi x}{\lambda } \right).$
Độ lệch pha của điểm M ở hai thời điểm ${{t}_{1}}$và ${{t}_{2}}$$\left( {{t}_{2}}>{{t}_{1}} \right)$ là $\Delta \varphi =\omega \left( {{t}_{2}}-{{t}_{1}} \right)=\omega \Delta t.$
3. Độ lệch pha của M tại thời điểm ${{\text{t}}_{\text{2}}}$so với điểm N tại thời điểm ${{t}_{1}}$
Ở cùng thời điểm ${{t}_{1}}$điểm M và N lệch pha nhau:$\frac{2\pi \left( {{x}_{2}}-{{x}_{1}} \right)}{\lambda }$
Ở thời điểm ${{t}_{2}}$điểm M $\left( {{t}_{2}} \right)$lệch pha so với điểm N$\left( {{t}_{1}} \right)$là:
$\Delta \varphi =\omega .\left( {{t}_{2}}-{{t}_{1}} \right)+\frac{2\pi \left( {{x}_{2}}-{{x}_{1}} \right)}{\lambda }.$
4. Xác định tính chất của các điểm M, N và chiều truyền sóng
a. ĐẶT VẤN ĐỀ
Bài toán: Xét 2 điểm M, N trên cùng một phương truyền sóng, sóng truyền từ M đến N,$MN=d$. Tại thời điểm ${{t}_{1}}$cho trạng thái của điểm M. Xác định tính chất của điểm N sau khoảng thời gian $\Delta t$.
b. Phương pháp giải:
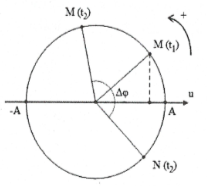
Sử dụng đường tròn lượng giác
Chú ý rằng sóng truyền từ M tới N nên trên đường tròn lượng giác điểm M chạy trước điểm N (như hình vẽ bên).
Sau khoảng thời gian$\Delta t$ta xác định đươc vị trí của điểm ${{M}_{2}}$. Dựa vào độ lệch pha giữa 2 điểm M và N để xác định trạng thái của điểm N.
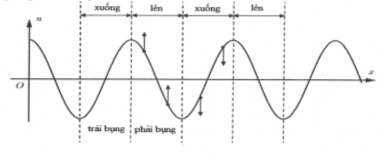
Ta có kết quả: những điểm nằm ở vế trái bụng sóng thì dao động đi xuống và những điểm nằm ở vế phải bụng sóng thì dao động đi lên.