Dạng 2: Xác định số lần vật qua một vị trí nào đó
(Xác định thời điểm vật đi qua vị trí x đã biết (hoặc v, a, Wt, Wđ, F lần thứ n).
Trong một chu kỳ T $\left( 2\pi \right)$vật đi qua li độ x = x0 hai lần nếu không kể đến chiều chuyển động, nếu kể đến chiều chuyển động (vật chuyển động theo chiều dương, hoặc vật chuyển động theo chiều âm thì sẽ đi qua một lần).
1. ĐẶT VẤN ĐỀ
Xét bài toán: Một vật dao động điều hòa trên trục Ox với phương trình $x=A\cos \left( \omega t+\varphi \right)$. Tính từ thời điểm ban đầu, vật có …… lần thứ n vào thời điểm nào.
2. PHƯƠNG PHÁP GIẢI
Bước 1:
Tìm trạng thái tại thời điểm ban đầu t = t0 dựa vào pha ban đầu ta suy ra trạng thái của vật $\left\{ \begin{array}{} {{x}_{0}}=? \\ {} \left[ \begin{array}{} {{v}_{0}}\text{ 0} \\ {} {{v}_{0}}\text{ 0} \\ \end{array} \right. \\ \end{array} \right.$.
Bước 2:
Phân tích trong một chu kỳ số lần N thỏa mãn điều kiện bài toán là bao nhiêu, sau đó ta lấy n chia cho N, khi đó ta có:$n=a.N+b$ .
Bước 3:
Thời điểm cần tìm sẽ là ${{t}_{n}}=\text{ }aT\text{ }+\text{ }{{t}_{2}}$
Thông thường khoảng thời gian t2 là những khoảng thời gian đẹp nên ta cần ghi nhớ sơ đồ các khoảng thời gian đặc biệt để làm bài toán một cách nhanh nhất.
Ta cần ghi nhớ sơ đồ cá khoảng thời gian đặc biệt trong dao động điều hòa:
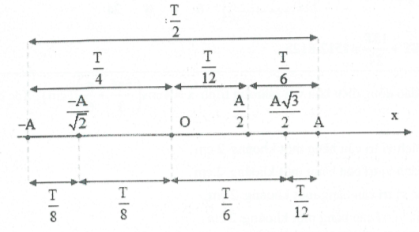
3. BÀI TẬP MINH HỌA DẠNG 2
| Bài tập 1: Một vật dao động điều hòa theo phương trình $x=10\cos \left( \frac{4\pi }{3}t+\frac{\pi }{6} \right)$cm. Kể từ$t\text{ }=\text{ }0$, vật qua vị trí $x=-5\sqrt{2}$cm
a) Lần thứ 2017 vào thời điểm là bao nhiêu b) Lần thứ 2018 vào thời điểm là bao nhiêu |
Lời giải chi tiết
a) Ta có: $T=\frac{2\pi }{\omega }=1,5\text{ (s)}$.
Trong một chu kì vật qua vị trí $x=-5\sqrt{2}$cm hai lần.
Tại ${{t}_{0}}=\text{ }0$ ta có $\left\{ \begin{array}{} x=5\sqrt{3}=\frac{A\sqrt{3}}{2} \\ {} v\text{ 0} \\ \end{array} \right.$(vật đang chuyển động theo chiều âm).
Lại có $\frac{2017}{2}=1008$ dư 1 nên${{t}_{2017}}=\text{ }1008T\text{ }+\text{ }{{t}_{1}}$, ở đây t1 là thời điểm đầu tiên vật qua tọa độ $x=-5\sqrt{2}$kể từ khi dao động. (Dư một nên t1 là thời điểm lần 1).

Dựa vào trục thời gian ta có:
${{t}_{1}}={{t}_{\left( \frac{A\sqrt{3}}{2}\to 0\to \frac{-A}{\sqrt{2}} \right)}}=\frac{T}{6}+\frac{T}{8}\Rightarrow {{t}_{2017}}=1008T+\frac{7T}{24}=1512,4375\text{s}$
b) Ở ý b ta thấy rằng $\frac{2018}{2}=1009$ nhiều bạn sẽ suy ra ${{t}_{2018}}=1009T$đây là cách làm sai.
Ta sẽ hiểu rằng $\frac{2018}{2}=1008$ dư 2 nên t2018 = 1008T + t1, ở đây t1 là thời điểm lần thứ 2 vật đi qua tọa độ $x=-5\sqrt{2}$kể từ khi dao động. (Dư 2 nên t1 là thời điểm lần thứ 2).

Dựa vào trục thời gian ta có: ${{t}_{1}}={{t}_{\left( \frac{A\sqrt{3}}{2}\to 0\to -\frac{A}{\sqrt{2}} \right)}}=\frac{T}{6}+\frac{T}{4}+\frac{T}{8}=\frac{13T}{24}$.
Suy ra ${{t}_{2018}}=1008T+\frac{13T}{24}=1512,8125$.
| Bài tập 2: Một vật dao động điều hòa theo phương trình $x=4\cos \left( \frac{5\pi t}{3}+\frac{\pi }{6} \right)$cm. Xác định thời điểm:
a) Thứ 2017 vật cách vị trí cân bằng một khoảng 2 cm. b) Thứ 2018 vật cách vị trí cân bằng một khoảng 2 cm. c) Thứ 2019 vật cách vị trí cân bằng một khoảng 2 cm. d) Thứ 2020 vật cách vị trí cân bằng một khoảng 2 cm. |
Lời giải chi tiết
a) Ta có $T=\frac{2\pi }{\omega }=1,2\left( \text{s} \right)$. Tại $t=0\Rightarrow \left\{ \begin{array}{} x=2\sqrt{3}=\frac{A\sqrt{3}}{2} \\ {} v\text{ 0} \\ \end{array} \right.$
Trong một chu kỳ vật cách VTCB một khoảng 2cm là 4 lần
Mặt khác:$\frac{2017}{4}=504$ dư 1 suy ra ${{t}_{2017}}=504T+{{t}_{1}}$ là thời điểm đầu tiên vật qua tọa độ $\left| x \right|=2$ kể từ khi dao động. (Dư một nên t1 là thời điểm lần 1)

Vẽ trục ta dễ dàng có được ${{t}_{1}}={{t}_{\left( \frac{A\sqrt{3}}{2}\to \frac{A}{2} \right)}}=\left( \frac{T}{6}-\frac{T}{12} \right)=\frac{T}{12}$
$\Rightarrow {{t}_{2017}}=504T+\frac{T}{12}=604,9s$
b) Ta có: $\frac{2018}{4}=504$ dư 2 suy ra ${{t}_{2018}}=504T+{{t}_{1}}$ với ${{t}_{1}}$ là thời điểm lần thứ hai vật qua tọa độ $\left| x \right|=2$ kể từ khi dao động.(Dư hai nên ${{t}_{2}}$ là thời điểm lần thứ 2).

Vẽ trục ta có được ${{t}_{1}}={{t}_{\left( \frac{A\sqrt{3}}{2}\to 0\to \frac{A}{2} \right)}}=\frac{T}{6}+\frac{T}{12}=\frac{T}{4}$
$\Rightarrow {{t}_{2018}}=504T+\frac{T}{4}=605,1s$
c) Ta có: Ta có: $\frac{2019}{4}=504$ dư 3 suy ra ${{t}_{2018}}=504T+{{t}_{1}}$ với ${{t}_{1}}$ là thời điểm lần thứ ba vật qua tọa độ $\left| x \right|=2$ kể từ khi dao động.(Dư ba nên ${{t}_{2}}$ là thời điểm lần thứ 3).

Vẽ trục ta có được ${{t}_{1}}={{t}_{\left( \frac{A\sqrt{3}}{2}\to 0\to \frac{-A}{2} \right)}}=\frac{T}{6}+\frac{T}{4}+\frac{T}{6}=\frac{7T}{12}$
$\Rightarrow {{t}_{2018}}=504T+\frac{7T}{12}=605,5s$
d) Ta có: Ta có: $\frac{2020}{4}=504$ dư 4 suy ra ${{t}_{2018}}=504T+{{t}_{1}}$ với ${{t}_{1}}$ là thời điểm lần thứ tư vật qua tọa độ $\left| x \right|=2$ kể từ khi dao động.(Dư bốn nên ${{t}_{2}}$ là thời điểm lần thứ 4).

Vẽ trục ta có được ${{t}_{1}}==\frac{T}{6}+\frac{T}{2}+\frac{T}{12}=\frac{3T}{4}$
$\Rightarrow {{t}_{2018}}=504T+\frac{3T}{4}=605,7s$
| Bài tập 3: Một vật dao động với phương trình $x=4\cos \left( 2\pi t+\frac{\pi }{4} \right)cm$
a) Vật qua vị trí $x\text{ }=2$cm theo chiều âm lần thứ 2017 vào thời điểm nào? b) Vật qua vị trí $x\text{ }=2$cm theo chiều dương lần thứ 2017 vào thời điểm nào? |
Lời giải chi tiết
a) Ta có: $T=\frac{2\pi }{\omega }=1s$
Trong một chu kì vật đi qua vị trí $x=2cm=\frac{A}{2}$theo chiều âm một lần
Tại thời điểm ban đầu $t=0\Rightarrow \left\{ \begin{array}{} x=2\sqrt{2} \\ {} v<0 \\ \end{array} \right.$
Ta có: $2017\text{ }=\text{ }2016\text{ }+\text{ }1$suy ra ${{t}_{2017}}=\text{ }2016\text{ }T\text{ }+\text{ }{{t}_{1}}$ với t1 là thời điểm lần thứ nhất vật đi qua vị trí $x\text{ }=\text{ }2$cm theo chiều âm
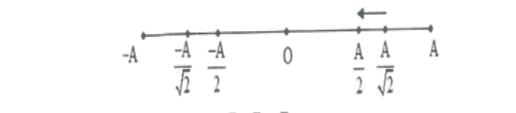
Vẽ trục ta có được ${{t}_{1}}={{t}_{\left( \frac{A\sqrt{2}}{2}\to \frac{A}{2} \right)}}=\frac{T}{8}+\frac{T}{12}=\frac{T}{24}$
Do đó: ${{t}_{2017}}=2016T+\frac{T}{24}=\frac{48385}{24}s$
b) Ta có: $2017\text{ }=\text{ }2016\text{ }+\text{ }1$ suy ra ${{t}_{2017}}=\text{ }2016\text{ }T\text{ }+\text{ }{{t}_{1}}$ với t1 là thời điểm lần thứ nhất vật đi qua vị trí $x\text{ }=\text{ }2$cm theo chiều dương
Vẽ trục thời gian ta có ${{t}_{1}}={{t}_{\left( \frac{A\sqrt{2}}{2}\to A\to \frac{A}{2} \right)}}=\frac{T}{8}+\frac{T}{2}+\frac{T}{12}=\frac{17T}{24}$
Vậy thời gian cần tìm là $t={{t}_{1}}+2016T=\frac{17T}{24}+2016T=\frac{48401}{21}s$
| Bài tập 4: Một vật dao động điều hòa với phương trình $x=6\cos \left( 4\pi t-\frac{\pi }{3} \right)cm$. Thời điểm thứ 2017 vật đi qua vị trí $x=-3\sqrt{2}cm$ là
A. $\frac{24205}{48}s$ B. $\frac{24199}{48}s$ C. $\frac{24172}{12}s$ D. $\frac{24205}{24}s$ |
Lời giải chi tiết
Ta có $T=\frac{2\pi }{\omega }=0,5(s)$ Trong một chu kì vật đi qua vị trí $x=-3\sqrt{2}cm$ hai lần
Tại: ${{t}_{0}}=0\Rightarrow \left\{ \begin{array}{} x=3=\frac{A}{2} \\ {} v>0 \\ \end{array} \right.$.(vật đang chuyển động theo chiều dương)
Lại có: $\frac{2017}{2}=1008$ dư 1 suy ra ${{t}_{7}}=1008T+{{t}_{1}}$ với ${{t}_{1}}$ là thời điểm đầu tiên vật qua tọa độ $x=-3\sqrt{2}cm$ kể từ khi dao động.(Dư một nên t1 là thời điểm lần thứ 1).

Dựa vào trục thời gian ta có: ${{t}_{1}}={{t}_{\left( \frac{A}{2}\to 0\to \frac{-A}{2} \right)}}=\frac{T}{6}+\frac{T}{4}+\frac{T}{8}\Rightarrow {{t}_{2017}}=1008T+\frac{13T}{24}=\frac{24205}{48}s$ Chọn A
| Bài tập 5: Một vật dao động điều hòa với phương trình $x=10\cos \left( \pi t-\frac{\pi }{4} \right)cm$. Thời điểm thứ 2018 vật đi qua vị trí có tốc độ bằng $5\pi $m/s là
A. $\frac{12107}{12}s$ B. $\frac{12101}{12}s$ C. $\frac{12099}{12}s$ D. $\frac{12113}{12}s$ |
Tại: ${{t}_{0}}=0\Rightarrow \left\{ \begin{array}{} x=\frac{A\sqrt{2}}{2} \\ {} v>0 \\ \end{array} \right.$. Ta có $\left| v \right|=5\pi =\frac{{{v}_{\max }}}{2}\Rightarrow \left| x \right|=\frac{A\sqrt{3}}{2}$
Trong một chu kì vật đi qua vị trí có $\left| x \right|=\frac{A\sqrt{3}}{2}$ bốn lần
Mặt khác Ta có: $\frac{2018}{4}=504$ dư 2 suy ra ${{t}_{2018}}=504T+{{t}_{1}}$ với ${{t}_{1}}$ là thời điểm lần thứ hai vật qua tọa độ $\left| x \right|=\frac{A\sqrt{3}}{2}$ kể từ khi dao động.(Dư hai nên t1 là thời điểm lần thứ 2).

Vẽ trục ta có được ${{t}_{1}}={{t}_{\left( \frac{A\sqrt{2}}{2}\to A\to \frac{A\sqrt{2}}{2} \right)}}=\frac{T}{8}+\frac{T}{12}=\frac{5T}{24}$
$$$\Rightarrow {{t}_{2018}}=504T+\frac{5T}{24}=\frac{12101}{24}s$. Chọn B
| Bài tập 6: [ Trích đề thi THPT QG năm 2017] Một chất điểm dao động điều hòa với phương trình $x=5\cos \left( 5\pi t-\frac{\pi }{3} \right)cm$(t tính bằng s). Kể từ khi t =0 , thời điểm đi qua vị trí có li độ x = -2,5 cm lần thứ 2017 là
A. 401,6 B. 403,4 C. 401,3 D. 403,5 |
Lời giải chi tiết
Ta có $T=\frac{2\pi }{\omega }=0,4(s)$ Trong một chu kì vật đi qua vị trí $x=-2,5cm$ 2 lần
Tại: $t=0\Rightarrow \left\{ \begin{array}{} x=2,5cm=\frac{A}{2} \\ {} v>0 \\ \end{array} \right.$.
Lại có: $\frac{2017}{2}=1008$ dư 1 suy ra ${{t}_{2017}}=1008T+{{t}_{1}}$ với ${{t}_{1}}$ là thời điểm đầu tiên vật qua tọa độ $x=-2,5$ kể từ khi dao động.(Dư một nên t1 là thời điểm lần thứ 1).

Dựa vào trục thời gian ta có:
${{t}_{1}}={{t}_{\left( \frac{A}{2}\to A\to \frac{-A}{2} \right)}}=\frac{T}{6}+\frac{T}{4}+\frac{T}{12}\Rightarrow {{t}_{2017}}=1008T+\frac{T}{2}=403,4s$ Chọn B
| Bài tập 7:[Trích đề thi đại học năm 2011]. Một vật dao động điều hòa với phương trình $x=4\cos \left( \frac{2\pi }{3}t \right)$(x tính bằng cm; t tính bằng s). Kể từ khi t = 0 , chất điểm đi qua vị trí có li độ x = -2 cm lần thứ 2011 tại thời điểm
A. 3016 s. B. 3015 s. C. 6030 s. D. 6031 s. |
Lời giải chi tiết
Tại thời điểm ban đầu $x\text{ }=\text{ }4\text{ }=\text{ }A$ , $T=\frac{2\pi }{\omega }=3(s)$
Lại có: $\frac{2011}{2}=1005$ dư 1 suy ra ${{t}_{2011}}=1005T+{{t}_{1}}$ với t1 là thời điểm đầu tiên vật qua tọa độ $x=-2$ kể từ khi dao động.(Dư một nên t1 là thời điểm lần thứ 1).
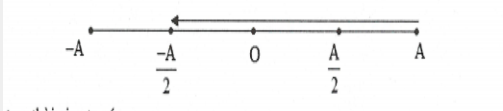
Dựa vào trục thời gian ta có:
${{t}_{1}}={{t}_{\left( A\to \frac{-A}{2} \right)}}=\frac{T}{4}+\frac{T}{12}\Rightarrow {{t}_{2011}}=1005T+\frac{T}{3}=3016s$ Chọn A
| Bài tập 8: Một chất điểm dao động điều hòa với phương trình $x=4\cos \left( 5\pi t-\frac{\pi }{6} \right)cm$( x tính bằng cm ; t tính bằng s). Thời điểm thứ 2018 vật đi qua vị trí có tốc độ bằng $v=10\pi $cm/s là
A. 401,6 B. 403,4. C. 401,3. D. 403,5. |
Lời giải chi tiết
Ta có $T=\frac{2\pi }{\omega }=0,4(s)$. Tại thời điểm $t=0\Rightarrow \left\{ \begin{array}{} x=2\sqrt{3} \\ {} v>0 \\ \end{array} \right.$
Tại: $v=-10\pi cm/s\Rightarrow \left[ \begin{matrix}\left\{ \begin{array}{} x=2\sqrt{3}cm \\ {} v=-10\pi cm/s \\ \end{array} \right. \\\left\{ \begin{array}{} x=-2\sqrt{3}cm \\ {} v=-10\pi cm/s \\ \end{array} \right. \\\end{matrix} \right.$.
Lại có: $\frac{2018}{4}=1008$ dư 2 suy ra ${{t}_{2018}}=1008T+{{t}_{1}}$ với t1 là thời điểm lần thứ 2 vật qua điểm có vận tốc $v=-10\pi \text{ }cm/s$.(Dư 2 nên t1 là thời điểm lần thứ 2).
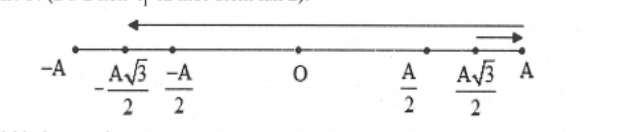
Dựa vào trục thời gian ta có:
${{t}_{1}}={{t}_{\left( \frac{A\sqrt{3}}{2}\to A\to \frac{-A\sqrt{3}}{2} \right)}}=\frac{T}{2}\Rightarrow {{t}_{2018}}=1008T+\frac{T}{2}=403,4s$ Chọn B.
$$$$
| Bài tập 9: Một chất điểm dao động điều hòa với phương trình $x=8\cos \left( \frac{5\pi t}{3}+\frac{\pi }{6} \right)$( x tính bằng cm ; t tính bằng s). Thời điểm vật đi qua vị trí có tốc độ bằng $v=4cm$lần thứ 2017 là
A. 3024,375s B. 3024,75s C. 3024,5s D. 3024,25s |
Lời giải chi tiết
Ta có $T=\frac{2\pi }{\omega }=3(s)$. Tại thời điểm ban đầu $\left\{ \begin{array}{} x=4\sqrt{3} \\ {} v<0 \\ \end{array} \right.$
Lại có: $\frac{2017}{2}=1008$ dư 1 suy ra ${{t}_{2017}}=1008T+{{t}_{1}}$, ở đây t1 là thời điểm đầu tiên vật qua tọa độ$x\text{ }=\text{ }4\text{ }cm~$kể từ khi dao động. (Dư một nên t1 là thời điểm lần thứ 1).

Dựa vào trục thời gian ta có ${{t}_{1}}={{t}_{\left( \frac{A\sqrt{3}}{2}\to \frac{A}{2} \right)}}=\frac{T}{6}-\frac{T}{12}\Rightarrow {{t}_{2017}}=1008T+\frac{T}{12}=3024,25s$ Chọn D
| Bài tập 10: Một chất điểm dao động điều hòa với phương trình $x=5\cos \left( 5\pi t+\frac{\pi }{6} \right)$( x tính bằng cm ; t tính bằng s). Thời điểm vật đi qua vị trí có tốc độ bằng $x\text{ }=-2,5cm~$ lần thứ 2017 là
A. 806,8 s. B. 806,7. C. 403,43. D. 806,633. |
Lời giải chi tiết
Ta có $T=\frac{2\pi }{\omega }=0,4(s)$. Tại thời điểm ban đầu $\left\{ \begin{array}{} x=2,5\sqrt{3} \\ {} v<0 \\ \end{array} \right.$
Lại có 2017 = 2016 + 1 nên${{t}_{2017}}=2016T\text{ }+\text{ }{{t}_{1}}$, ở đây t1 là thời điểm đầu tiên vật qua tọa độ $x\text{ }=\text{ }-2,5\text{ }cm~$theo chiều dương kể từ khi dao động.
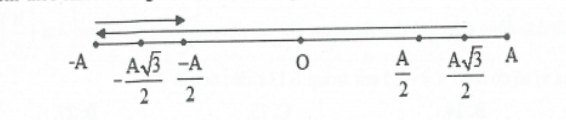
Dựa vào trục thời gian ta có:
${{t}_{1}}={{t}_{\left( \frac{A\sqrt{3}}{2}\to A\to \frac{A}{2} \right)}}=\frac{T}{6}+\frac{T}{4}+\frac{T}{6}\Rightarrow {{t}_{2017}}=2016T+\frac{7T}{12}=806,633s$ Chọn D
| Bài tập 11: [ Trích đề thi thử CHuyên ĐH Vinh 2017] Một vật dao động điều hòa với phương trình $x=A\cos \left( 2\pi t-\frac{\pi }{6} \right)cm$( t tính bằng s). Tính từ thời điểm ban đầu t = 0, khoảng thời gian vật đi qua vị trí cân bằng lần thứ 2017. Theo chiều âm là
A. $\frac{6049}{3}s$ B. $\frac{6052}{3}s$ C. $2016s$ D. $2017s$ |
Lời giải chi tiết
Ta có $T=\frac{2\pi }{\omega }=1(s)$. Tại thời điểm ban đầu $\left\{ \begin{array}{} x=\frac{A\sqrt{3}}{2} \\ {} v>0 \\ \end{array} \right.$
Lại có $2017\text{ }=\text{ }2016\text{ }+\text{ }1$ nên ${{t}_{2017\text{ }}}=2016T\text{ }+\text{ }{{t}_{1}}$ , ở đây t1 là thời điểm đầu tiên vật qua vị trí cân bằng theo chiều âm.
Dựa vào trục thời gian ta có ${{t}_{1}}=\frac{T}{12}+\frac{T}{4}$
Suy ra$T=2016T+\frac{T}{12}+\frac{T}{4}=\frac{6049}{3}s$ Chọn A
