VẤN ĐỀ 1. ĐIỆN TÍCH, LỰC ĐIỆN TRƯỜNG, THUYẾT ELECTRON
LÝ THUYẾT TRỌNG TÂM
– Vật nhiễm điện (vật mang điện, điện tích) là vật có khả năng hút được các vật nhẹ. Có 3 hiện tượng nhiễm điện: nhiễm điện do cọ xát, nhiễm điện do tiếp xúc và nhiễm điện do hưởng ứng.
– Điện tích điểm: là vật tích điện có kích thước rất nhỏ so với khoảng cách tới điểm ta xét.
– Hai loại điện tích: Điện tích dưong và điện tích âm (cùng dấu thì đẩy nhau, trái dấu thì hút nhau).
– Định luật Cu-Lông: Lực hút hay đẩy giữa 2 điện tích điểm có phương trùng với đường thẳng nối 2 điện tích điểm đó, có độ lớn tỉ lệ thuận với tích độ lớn của hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng: ${{F}_{0}}=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}$
(với ${{q}_{1}},{{q}_{2}}$ là điện tích; $k={{9.10}^{9}}$ là hằng số điện; r (m) là khoảng cách giữa 2 điện tích điểm).
– Hằng số điện môi (e) đặc trưng cho tính cách điện của chất cách điện. Lực tương tác giữa hai điện tích trong điện môi giảm đi e lần so với khi đặt nó trong chân không $F=\frac{{{F}_{0}}}{\varepsilon }=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{\varepsilon {{r}^{2}}};\,\,\,\varepsilon $ luôn $\ge 1$ (e của không khí » chân không = 1).
– Thuyết electron: (giải thích các hiện tượng nhiễm điện)
+) Electron rất linh động, có thể bút ra khỏi nguyên tử, di chuyển từ nguyên tử này sang nguyên tử khác, di chuyến từ vật này sang vật khác và làm cho các vật nhiễm điện.
+) Nguyên tử mất (e) trở thành ion dương (+), nguyên tử nhận (e) trở thành ion âm (-).
+) Sự cư trú và di chuyển của các electron tạo nên các hiện tượng về điện và tính chất điện.
– Vật dẫn điện là vật chứa nhiều điện tích tự do, vật cách điện chứa ít hoặc rất ít điện tích tự do.
– Định luật bảo toàn điện tích: Trong một hệ cô lập về điện (hệ không trao đổi điện tích với các hệ khác), tổng đại số của các điện tích là không đổi ${{q}_{1}}+{{q}_{2}}=q_{1}^{‘}+q_{2}^{‘}$
CÁC DẠNG BÀI TẬP
DẠNG 1: LỰC TƯƠNG TÁC GIỮA HAI ĐIỆN TÍCH ĐIỂM
PHƯƠNG PHÁP GIẢI
Lực tương tác giữa 2 điện tích điểm là lực Culông: $F={{9.10}^{9}}\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{\varepsilon {{r}^{2}}}$
Bài toán cho tích độ lớn 2 điện tích và tổng độ lớn 2 điện tích thì AD hệ thức Vi-ét:
$\left\{ \begin{array}{} {{q}_{1}}+{{q}_{2}}=S \\ {} {{q}_{1}}{{q}_{2}}=P \\ \end{array} \right.$ thì ${{q}_{1}};{{q}_{2}}$ là nghiệm của phương trình bậc 2: ${{X}^{2}}-S.X+P=0$
Chú ý: Cho 2 vật tích điện ${{q}_{1}}$ và ${{q}_{2}}$ tiếp xúc với nhau rồi tách ra thì điện tích chúng sẽ bằng nhau:
$q_{1}^{‘}=q_{2}^{‘}=\frac{{{q}_{1}}+{{q}_{2}}}{2}$
BÀI TẬP LUYỆN TẬP DẠNG 1
| Bài tập 1: Hai điện tích điểm ${{q}_{1}}={{2.10}^{-8}}C,{{q}_{2}}=-{{10}^{-8}}C$ đặt cách nhau 20cm trong không khí. Xác định lực tương tác giữa chúng? |
Lời giải chi tiết
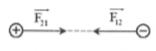
Lực tương tác giữa hai điện tích điểm ${{q}_{1}},{{q}_{2}}$ là $\overrightarrow{{{F}_{12}}},\overrightarrow{{{F}_{21}}}$ có:
Phương là đường thẳng nối hai điện tích điểm.
![]() ${{q}_{1}}.{{q}_{2}}<0\Rightarrow $ chiều là lực hút
${{q}_{1}}.{{q}_{2}}<0\Rightarrow $ chiều là lực hút
Độ lớn ${{F}_{12}}={{F}_{21}}=k\frac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}={{9.10}^{9}}.\frac{{{2.10}^{-8}}{{.10}^{-8}}}{0,{{2}^{2}}}=4,{{5.10}^{-5}}N$
| Bài tập 2: Hai điện tích đặt cách nhau một khoảng r trong không khí thì lực tương tác giữa chúng là ${{2.10}^{-3}}N$. Nếu khoảng cách đó mà đặt trong môi trường điện môi thì lực tương tác giữa chúng là ${{10}^{-3}}N$
a) Xác định hằng số điện môi. b) Để lực tương tác giữa hai điện tích đó khi đặt trong điện môi bằng lực tương tác giữa hai điện tích khi đặt trong không khí thì khoảng cách giữa hai điện tích là bao nhiêu? Biết khoảng cách giữa hai điện tích này trong không khí là 20 cm. |
Lời giải chi tiết
a) Biểu thức lực tương tác giữa hai điện tích trong không khí và trong điện môi được xác định bởi:
$\left\{ \begin{array}{} {{F}_{0}}=k\frac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}} \\ {} F=k\frac{{{q}_{1}}{{q}_{2}}}{\varepsilon {{r}^{2}}} \\ \end{array} \right.\Rightarrow \varepsilon =\frac{{{F}_{0}}}{F}=2$
b) Để lực tương tác giữa hai điện tích khi đặt trong điện môi bằng lực tương tác giữa hai điện tích khi ta đặt trong không khí thì khoảng cách giữa hai điện tích bây giờ là r’:
$\left\{ \begin{array}{} {{F}_{0}}=k\frac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}} \\ {} F=k\frac{{{q}_{1}}{{q}_{2}}}{\varepsilon r{{‘}^{2}}} \\ \end{array} \right.\Rightarrow {{F}_{0}}=F’\Rightarrow r’=\frac{r}{\sqrt{\varepsilon }}=10\sqrt{2}cm$
| Bài tập 3: Cho hai điện tích điểm ${{q}_{1}}={{10}^{-8}}C,{{q}_{2}}=-{{2.10}^{-8}}C$ đặt tại hai điểm A và B cách nhau 10 cm trong không khí.
a) Tìm lực tương tác tĩnh điện giữa hai điện tích. b) Muốn lực hút giữa chúng là $7,{{2.10}^{-4}}N$ . Thì khoảng cách giữa chúng bây giờ là bao nhiêu? c) Thay ${{q}_{2}}$ bởi điện tích điểm ${{q}_{3}}$ cũng đặt tại B như câu b) thì lực lực đẩy giữa chúng bây giờ là $3,{{6.10}^{-4}}N$. Tìm ${{q}_{3}}$ ? d) Tính lực tương tác tĩnh điện giữa q1 và q3 như trong câu c (chúng đặt cách nhau 10 cm) trong chất parafin có hằng số điện môi e = 2 |
Lời giải chi tiết
a) Lực tương tác giữa hai điện tích là: $F=k\frac{\left| {{q}_{1}}.{{q}_{2}} \right|}{{{r}^{2}}}={{9.10}^{9}}.\frac{\left| {{10}^{-8}}.-{{2.10}^{-8}} \right|}{0,{{1}^{2}}}=1,{{8.10}^{-4}}N$
b) Vì lực F tỉ lệ nghịch với bình phương khoảng cách nên khi $F’=7,{{2.10}^{-4}}N=4F$ (tăng lên 4 lần) thì khoảng cách r giảm 2 lần: $r’=\frac{r}{2}=\frac{0,1}{2}=0,05\left( m \right)=5\left( cm \right)$
c) $F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}\Rightarrow \left| {{q}_{3}} \right|=\frac{F.{{r}^{2}}}{k.\left| {{q}_{1}} \right|}=\frac{3,{{6.10}^{-4}}.0,{{1}^{2}}}{{{9.10}^{9}}{{.10}^{-8}}}={{4.10}^{-8}}C$ . Vì lực đẩy nên ${{q}_{3}}$ cùng dấu ${{q}_{1}}$
d) Ta có: lực F tỉ lệ nghịch với e nên $F’=\frac{F}{\varepsilon }=\frac{3,{{6.10}^{-4}}}{2}=1,{{8.10}^{-4}}N$
| Bài tập 4: Trong nguyên tử Hidro, electron chuyển động tròn đều quanh hạt nhân theo quỹ đạo tròn có bán kính ${{5.10}^{-9}}cm$
a ) Xác định lực hút tĩnh điện giữa electron và hạt nhân. b) Xác định tần số chuyển động của electron. Biết khối lượng của electron là $9,{{1.10}^{-31}}kg$ |
Lời giải chi tiết
a) Lực hút tĩnh điện giữa electron và hạt nhân:
$F=k\frac{{{e}^{2}}}{{{r}^{2}}}={{9.10}^{9}}{{\left( \frac{1,{{6.10}^{-19}}}{{{5.10}^{-11}}} \right)}^{2}}=9,{{2.10}^{-8}}N$
b) Electron chuyển động tròn quanh hạt nhân, nên lực tĩnh điện đóng vai trò là lực hướng tâm:
$F=k\frac{{{e}^{2}}}{{{r}^{2}}}=m{{\omega }^{2}}r\Rightarrow \omega =\sqrt{\frac{F}{mr}}=\sqrt{\frac{9,{{2.10}^{-4}}}{9,{{1.10}^{-31}}{{.5.10}^{-11}}}}=4,{{5.10}^{16}}rad/s$
Tần số chuyển động của electron là: $f=\frac{\omega }{2\pi }=0,{{72.10}^{26}}Hz$
| Bài tập 5: Hai vật nhỏ giống nhau (có thể coi là chất điểm), mỗi vật thừa một electron. Tìm khối lượng của mỗi vật để lực tĩnh điện bằng lực hấp dẫn. Cho hằng số hấp dẫn $G=6,{{67.10}^{-11}}N.{{m}^{2}}/k{{g}^{2}}$ |
Lời giải chi tiết
Lực tĩnh điện : $F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}=k\frac{{{q}^{2}}}{{{r}^{2}}}$ ; lực hấp dẫn $F’=G.\frac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}=G.\frac{{{m}^{2}}}{{{r}^{2}}}$
Để F = F’ thì $k\frac{{{q}^{2}}}{{{r}^{2}}}=G\frac{{{m}^{2}}}{{{r}^{2}}}\Rightarrow m=\left| q \right|\sqrt{\frac{k}{G}}=1,{{6.10}^{-19}}\sqrt{\frac{{{9.10}^{9}}}{6,{{67.10}^{-11}}}}=1,{{86.10}^{-9}}\left( kg \right)$
| Bài tập 6: Hai điện tích q1 và q2 đặt cách nhau 20 cm trong không khí, chúng đẩy nhau một lực F = 1,8 N. Biết ${{q}_{1}}+{{q}_{2}}=-{{6.10}^{-6}}C$ và $\left| {{q}_{2}} \right|>\left| {{q}_{1}} \right|$ . Xác định dấu của điện tích ${{q}_{1}},{{q}_{2}}$ . Vẽ các vecto lực điện tác dụng lên các điện tích. Tính ${{q}_{1}},{{q}_{2}}$ |
Lời giải chi tiết
![]()
Hai điện tích đẩy nhau nên chúng cùng dấu, mặt khác tổng hai điện tích này là số âm do đó có hai điện tích đều âm:
$F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}\Rightarrow \left| {{q}_{1}}{{q}_{2}} \right|=\frac{F{{r}^{2}}}{k}={{8.10}^{-12}}$
Kết hợp với giả thuyết ${{q}_{1}}+{{q}_{2}}=-{{6.10}^{-6}}C$, ta có hệ phương trình $\left\{ \begin{array}{} {{q}_{1}}+{{q}_{2}}=-{{6.10}^{-6}} \\ {} {{q}_{1}}{{q}_{2}}={{8.10}^{-12}} \\ \end{array} \right.$
Áp dụng hệ thức Viét Þ ${{q}_{1}},{{q}_{2}}$ là hai nghiệm của phương trình ${{X}^{2}}-\left( -{{6.10}^{-6}} \right)X+{{8.10}^{-12}}=0$
$\Rightarrow \left[ \begin{array}{} \left\{ \begin{array}{} {{q}_{1}}=-{{2.10}^{-6}}C \\ {} {{q}_{2}}=-{{4.10}^{-6}}C \\ \end{array} \right. \\ {} \left\{ \begin{array}{} {{q}_{1}}=-{{4.10}^{-6}}C \\ {} {{q}_{2}}=-{{2.10}^{-6}}C \\ \end{array} \right. \\
\end{array} \right.$ vì $\left| {{q}_{2}} \right|>\left| {{q}_{1}} \right|\Rightarrow \left\{ \begin{array}{} {{q}_{1}}=-{{4.10}^{-6}}C \\ {} {{q}_{2}}=-{{2.10}^{-6}}C \\ \end{array} \right.$
| Bài tập 7: Cho hai quả cầu kim loại nhỏ, giống nhau, tích điện và cách nhau 20 cm thì chúng hút nhau một lực bằng 1,2 N. Cho chúng tiếp xúc với nhau rồi tách chúng ra đến khoảng cách như cũ thì chúng đẩy nhau một lực bằng lực hút. Tính điện tích lúc đầu của mỗi quả cầu. |
Lời giải chi tiết
Hai quả cầu ban đầu hút nhau nên chúng mang điện trái dấu.
Từ giả thuyết bài toán, ta có $\left\{ \begin{array}{} \left| {{q}_{1}}{{q}_{2}} \right|=-{{q}_{1}}{{q}_{2}}=\frac{F{{r}^{2}}}{k}=\frac{16}{3}{{10}^{-12}} \\ {} {{\left( \frac{{{q}_{1}}+{{q}_{2}}}{2} \right)}^{2}}=\frac{F{{r}^{2}}}{k}\Rightarrow {{q}_{1}}+{{q}_{2}}=\pm \frac{\sqrt{192}}{3}{{10}^{-6}}. \\ \end{array} \right.$
Áp dụng hệ thức Viét $\Rightarrow {{q}_{1}},{{q}_{2}}$ là nghiệm của phương trình: ${{X}^{2}}\pm \frac{\sqrt{192}}{3}{{10}^{-6}}.X+\frac{16}{3}{{.10}^{-12}}=0$
$\Rightarrow \left\{ \begin{array}{} {{q}_{1}}=0,{{96.10}^{-6}}C \\ {} {{q}_{2}}=-5,{{58.10}^{-6}}C \\ \end{array} \right.$ hoặc $\Rightarrow \left\{ \begin{array}{} {{q}_{1}}=-5,{{58.10}^{-6}}C \\ {} {{q}_{2}}=0,{{96.10}^{-6}}C \\ \end{array} \right.$
DẠNG 2: LỰC ĐIỆN TỔNG HỢP TÁC DỤNG LÊN MỘT ĐIỆN TÍCH
PHƯƠNG PHÁP GIẢI
– Khi một điện tích điểm q chịu tác dụng của nhiều lực tác dụng $\overrightarrow{{{F}_{1}}},\overrightarrow{{{F}_{2}}},…$ do các điện tích điểm ${{q}_{1}},{{q}_{2}},…$ gây ra thì hợp lực tác dụng lên q là: $\overrightarrow{F}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}+\overrightarrow{{{F}_{3}}}+…+\overrightarrow{{{F}_{n}}}$
– Các bước tìm hợp lực $\overrightarrow{F}$ do các điện tích${{q}_{1}};{{q}_{2}}$… tác dụng lên điện tích ${{q}_{0}}$:
Bước 1: Xác định vị trí điểm đặt các điện tích (vẽ hình).
Bước 2: Tính độ lớn các lực ${{F}_{1}};{{F}_{2}}$ lần lượt do ${{q}_{1}};{{q}_{2}}$ tác dụng lên ${{q}_{0}}$.
Bước 3: Vẽ hình các vectơ lực $\overrightarrow{{{F}_{1}}},\overrightarrow{{{F}_{2}}}$
Bước 4: Từ hình vẽ xác định phương, chiều, độ lớn của hợp lực $\overrightarrow{F}$.
– Các trường hợp đặc biệt:
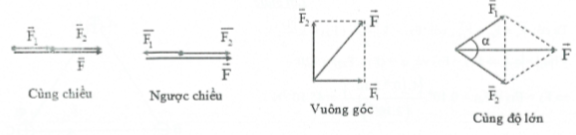
$\overrightarrow{{{F}_{1}}};\overrightarrow{{{F}_{2}}}$ cùng chiều thì $F={{F}_{1}}+{{F}_{2}}\left( \alpha =0;cos\alpha =1 \right)$
$\overrightarrow{{{F}_{1}}};\overrightarrow{{{F}_{2}}}$ ngược chiều thì $F=\left| {{F}_{1}}-{{F}_{2}} \right|\left( \alpha =\pi ;cos\alpha =-1 \right)$
$\overrightarrow{{{F}_{1}}};\overrightarrow{{{F}_{2}}}$ vuông góc thì $F=\sqrt{F_{1}^{2}+F_{2}^{2}}\left( \alpha =90{}^\circ ;cos\alpha =0 \right)$
$\overrightarrow{{{F}_{1}}};\overrightarrow{{{F}_{2}}}$ cùng độ lớn $\left( {{F}_{1}}={{F}_{2}} \right)$ thì $F=2{{F}_{1}}\cos \frac{\alpha }{2}$
Tổng quát ${{F}^{2}}=F_{1}^{2}+F_{2}^{2}+2{{F}_{1}}{{F}_{2}}\cos \alpha $ (a là góc hợp bởi $\overrightarrow{{{F}_{1}}};\overrightarrow{{{F}_{2}}}$)
BÀI TẬP LUYỆN TẬP DẠNG 2
| Bài tập 8: Hai điện tích ${{q}_{1}}={{8.10}^{-8}}C;{{q}_{2}}=-{{8.10}^{-8}}C$ đặt tại A, B trong không khí (AB = 6cm). Xác định lực tác dụng lên ${{q}_{3}}={{8.10}^{-8}}C$, nếu
a) CA = 4 cm, CB = 2 cm. b) CA = 4 cm, CB = 10 cm. c) CA = CB = 5 cm. |
Lời giải chi tiết
Lực tổng hợp tác dụng lên ${{q}_{3}}$ là: $\overrightarrow{F}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}$
a) Vì AC + CB = AB nên C nằm trong đoạn AB.
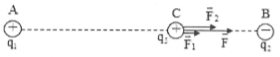
${{q}_{1}},{{q}_{3}}$ cùng dấu nên $\overrightarrow{{{F}_{1}}}$ là lực đẩy
${{q}_{2}},{{q}_{3}}$ cùng dấu nên $\overrightarrow{{{F}_{2}}}$ là lực hút
Do $\overrightarrow{{{F}_{1}}}$và $\overrightarrow{{{F}_{2}}}$cùng chiều Þ $\overrightarrow{F}$cùng chiều $\overrightarrow{{{F}_{1}}}$,$\overrightarrow{{{F}_{2}}}$
$F={{F}_{1}}+{{F}_{2}}=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{A{{C}^{2}}}+k\frac{\left| {{q}_{2}}{{q}_{3}} \right|}{B{{C}^{2}}}={{9.10}^{9}}.\left( \frac{\left| {{8.10}^{-8}}{{.8.10}^{-8}} \right|}{{{\left( {{4.10}^{-2}} \right)}^{2}}}+\frac{\left| {{8.10}^{-8}}{{.8.10}^{-8}} \right|}{{{\left( {{2.10}^{-2}} \right)}^{2}}} \right)=0,18N$
b) Vì CB – CA = AB nên C nằm trên đường AB, ngoài khoảng AB, về phía A.

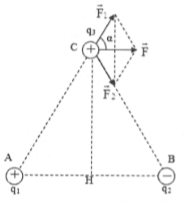
${{F}_{1}}={{9.10}^{9}}\frac{{{8.10}^{-8}}{{.8.10}^{-8}}}{{{\left( {{4.10}^{-2}} \right)}^{2}}}={{36.10}^{-3}}N;\,\,\,\,{{F}_{2}}={{9.10}^{9}}\frac{{{8.10}^{-8}}{{.8.10}^{-8}}}{{{\left( {{10.10}^{-2}} \right)}^{2}}}=5,{{76.10}^{-3}}N$ Do $\overrightarrow{{{F}_{1}}}$ và $\overrightarrow{{{F}_{2}}}$ ngược chiều, $\overrightarrow{{{F}_{1}}}>\overrightarrow{{{F}_{2}}}$
$\Rightarrow \overrightarrow{F}$ cùng chiều $\overrightarrow{{{F}_{1}}}$và $F={{F}_{1}}-{{F}_{2}}=30,{{24.10}^{-3}}N$
c) Vì C cách đều A, B nên c nằm trên đường trung trực của đoạn AB
${{F}_{1}}=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{A{{C}^{2}}}=23,{{04.10}^{-3}}N;\,\,\,\,\,{{F}_{2}}=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{C{{B}^{2}}}=23,{{04.10}^{-3}}N$
Vì ${{F}_{1}}={{F}_{2}}$ nên $\overrightarrow{F}$ nằm trên phân giác góc $\left( \overrightarrow{{{F}_{1}}};\overrightarrow{{{F}_{2}}} \right)$
$\Rightarrow \overrightarrow{F}\bot CH$(phân giác của 2 góc kề bù) $\Rightarrow \overrightarrow{F}//AB$
$\Rightarrow \alpha =\left( \overrightarrow{{{F}_{1}}};\overrightarrow{{{F}_{2}}} \right)=CAB$
$F=2{{F}_{1}}\cos \alpha =2{{F}_{1}}\frac{AH}{AC}=2.23,{{04.10}^{-5}}.\frac{3}{5}=27,{{65.10}^{-3}}N$
| Bài tập 9: Ba điện tích điểm ${{q}_{1}}={{4.10}^{-8}}C;{{q}_{2}}=-{{4.10}^{-8}}C;{{q}_{3}}={{5.10}^{-8}}C$ đặt trong không khí tại 3 đỉnh ABC của 1 tam giác đều, cạnh a = 2cm. Xác định vector lực tác dụng lên ${{q}_{3}}$. |
Lời giải chi tiết
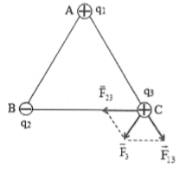
Ta có: $\overrightarrow{{{F}_{3}}}=\overrightarrow{{{F}_{13}}}+\overrightarrow{{{F}_{23}}}$ với ${{F}_{13}}=k\frac{\left| {{q}_{1}}{{q}_{3}} \right|}{{{a}^{2}}};{{F}_{23}}=k\frac{\left| {{q}_{2}}{{q}_{3}} \right|}{{{a}^{2}}}$
Vì $\left| {{q}_{1}} \right|=\left| {{q}_{2}} \right|\Rightarrow {{F}_{13}}={{F}_{23}}$ và $\alpha =\left( {{F}_{13}},{{F}_{23}} \right)=120{}^\circ $
$\Rightarrow {{F}_{3}}={{F}_{13}}={{F}_{23}}={{9.10}^{9}}.\frac{\left| {{4.10}^{-8}}{{.5.10}^{-8}} \right|}{{{\left( {{2.10}^{-2}} \right)}^{2}}}={{45.10}^{-3}}N$
| Bài tập 10: Người ta đặt 3 điện tích ${{q}_{1}}={{8.10}^{-9}}C,{{q}_{2}}={{q}_{3}}=-{{8.10}^{-9}}C$tại ba đỉnh của tam giác đều ABC cạnh
a = 6cm trong không khí. Xác định lực tác dụng lên ${{q}_{0}}={{6.10}^{-9}}C$đặt tại tâm O của tam giác. |
Lời giải chi tiết
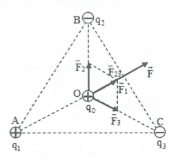
Ta có ${{r}_{1}}={{r}_{2}}={{r}_{3}}=\frac{2}{3}OA=2\sqrt{3}cm$
${{F}_{1}}=k\frac{\left| {{q}_{1}}{{q}_{0}} \right|}{A{{O}^{2}}}=3,{{6.10}^{-4}}(N);{{F}_{2}}=k\frac{\left| {{q}_{0}}{{q}_{2}} \right|}{B{{O}^{2}}}=3,{{6.10}^{-4}}(N)$
${{F}_{3}}=k\frac{\left| {{q}_{3}}{{q}_{0}} \right|}{C{{O}^{2}}}=3,{{6.10}^{-4}}(N)$
Lực tác dụng lên ${{q}_{0}}:\overrightarrow{F}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}+\overrightarrow{{{F}_{3}}}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{23}}}$
Ta có: ${{F}_{23}}=\sqrt{F_{2}^{2}+F_{3}^{2}+2{{F}_{2}}{{F}_{3}}\cos 120{}^\circ }=3,{{6.10}^{-4}}N$
Vì DABC đều nên $\overrightarrow{{{F}_{23}}}\uparrow \uparrow \overrightarrow{{{F}_{1}}}\Rightarrow F={{F}_{1}}+{{F}_{23}}=7,{{2.10}^{-4}}N$
| Bài tập 11: Hai điện tích điểm ${{q}_{1}}={{3.10}^{-8}}C,{{q}_{2}}={{2.10}^{-8}}C$tại 2 điểm A và B trong chân không, AB = 5cm. Điện tích ${{q}_{0}}=-{{2.10}^{-8}}C$ đặt tại M, MA = 4cm, MB = 3 cm. Xác định lực điện tổng hợp tác dụng lên ${{q}_{0}}$ |
Lời giải chi tiết
Nhận thấy $A{{B}^{2}}=A{{M}^{2}}+M{{B}^{2}}\Rightarrow $ tam giác AMB vuông tại M.
Gọi $\overrightarrow{{{F}_{1}}},\overrightarrow{{{F}_{2}}}$ lần lượt là lực do điện tích ${{q}_{1}},{{q}_{2}}$ tác dụng lên ${{q}_{0}}$
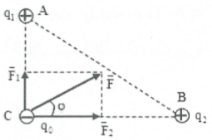
$\left\{ \begin{array}{} {{F}_{1}}=k\frac{\left| {{q}_{1}}{{q}_{0}} \right|}{A{{M}^{2}}}={{9.10}^{9}}.\frac{\left| {{3.10}^{-8}}{{.2.10}^{-8}} \right|}{0,{{04}^{2}}}=3,{{375.10}^{-3}}N \\ {} {{F}_{2}}=k\frac{\left| {{q}_{2}}{{q}_{0}} \right|}{B{{M}^{2}}}={{9.10}^{9}}.\frac{\left| {{2.10}^{-8}}{{.2.10}^{-8}} \right|}{0,{{03}^{2}}}={{4.10}^{-3}}N \\ \end{array} \right.$
$\overrightarrow{F}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}\Rightarrow F=\sqrt{F_{1}^{2}+F_{2}^{2}}=5,{{234.10}^{-3}}N$
Ta có: $\tan \varphi =\frac{{{F}_{1}}}{{{F}_{2}}}=\frac{27}{32}\Rightarrow \varphi \approx 40{}^\circ $
Vậy lực tổng hợp tác dụng lên ${{q}_{0}}$ có điểm đặt tại C, phương tạo với $\overrightarrow{{{F}_{2}}}$ một góc $\varphi \approx 40{}^\circ $ và độ lớn bằng $5,{{234.10}^{-3}}N$
DẠNG 3: SỰ CÂN BẰNG CỦA MỘT ĐIỆN TÍCH
PHƯƠNG PHÁP GIẢI
– Khi một điện tích q đứng yên thì họp lực tác dụng lên q sẽ bằng $\overrightarrow{0}$:
$\overrightarrow{F}=\overrightarrow{{{F}_{10}}}+\overrightarrow{{{F}_{20}}}=0\Rightarrow \overrightarrow{{{F}_{10}}}=-\overrightarrow{{{F}_{20}}}\Rightarrow \left\{ \begin{array}{} \overrightarrow{{{F}_{10}}}\uparrow \downarrow \overrightarrow{{{F}_{20}}} \\ {} {{F}_{10}}={{F}_{20}} \\ \end{array} \right.$
– Dạng này có 2 loại:
+) Loại bài chỉ có lực điện.
+) Loại bài có thêm các lực cơ học: Trọng lực: p = mg (luôn hướng xuống), Lực căng dây T, lực đàn hồi của lò xo: $F=k.\Delta l=k\left( \ell -{{\ell }_{o}} \right);…$
BÀI TẬP LUYỆN TẬP DẠNG 3
| Bài tập 12: Hai điện tích điểm ${{q}_{1}}={{10}^{-8}}C,{{q}_{2}}={{4.10}^{-8}}C$ đặt tại A và B cách nhau 9cm trong chân không. Phải đặt điện tích ${{q}_{3}}={{2.10}^{-6}}C$ tại đâu để điện tích ${{q}_{3}}$ nằm cân bằng? |
Lời giải chi tiết
Điều kiện cân bằng của ${{q}_{3}}$ : $\overrightarrow{{{F}_{13}}}+\overrightarrow{{{F}_{23}}}=0\Rightarrow \overrightarrow{{{F}_{13}}}=-\overrightarrow{{{F}_{23}}}\Rightarrow $ điểm C phải thuộc AB
Vì ${{q}_{1}},{{q}_{2}}$ cùng dấu nên C phải nằm trong AB
${{F}_{13}}={{F}_{23}}\Leftrightarrow k\frac{\left| {{q}_{1}}{{q}_{3}} \right|}{C{{A}^{2}}}=k\frac{\left| {{q}_{2}}{{q}_{3}} \right|}{C{{B}^{2}}}\Rightarrow \frac{\left| {{q}_{1}} \right|}{C{{A}^{2}}}=\frac{\left| {{q}_{2}} \right|}{C{{B}^{2}}}\Rightarrow \frac{CB}{CA}=2\Rightarrow CB=2CA\left( 1 \right)\Rightarrow $ C gần A hơn.

Mặt khác: CA + CB = 9 (2)
Từ (1) và (2) $\Rightarrow CA=3cm,CB=6cm$
| Bài tập 13: Tại ba đỉnh của một tam giác đều trong không khí, đặt ba điện tích giống nhau ${{q}_{1}}={{q}_{2}}={{q}_{3}}=q={{6.10}^{-7}}C$ . Hỏi phải đặt điện tích ${{q}_{0}}$ tại đâu, có giá trị bao nhiêu để hệ điện tích cân bằng? |
Lời giải chi tiết
Xét điều kiện cân bằng của ${{q}_{3}}:\overrightarrow{{{F}_{13}}}+\overrightarrow{{{F}_{23}}}+\overrightarrow{{{F}_{03}}}=\overrightarrow{{{F}_{3}}}+\overrightarrow{{{F}_{03}}}=\overrightarrow{0}$
Với ${{F}_{13}}={{F}_{23}}=k\frac{{{q}^{2}}}{{{a}^{2}}}$ và $\left( \overrightarrow{{{F}_{13}}};\overrightarrow{{{F}_{23}}} \right)=60{}^\circ \Rightarrow {{F}_{3}}=2{{F}_{13}}\cos 30{}^\circ ={{F}_{13}}\sqrt{3}=\sqrt{3}k.\frac{{{q}^{2}}}{{{a}^{2}}}$
${{F}_{3}}$ có phương là đường phân giác góc C, lại có $\overrightarrow{{{F}_{03}}}\uparrow \downarrow \overrightarrow{{{F}_{3}}}$ nên ${{q}_{0}}$ nằm trên phân giác góc C.
Tương tự, ${{q}_{0}}$ cũng thuộc phân giác các góc A và B. Vậy ${{q}_{0}}$ tại trọng tâm G của ABC.
Vì $\overrightarrow{{{F}_{03}}}\uparrow \downarrow \overrightarrow{{{F}_{3}}}$ nên $\overrightarrow{{{F}_{03}}}$ hướng về phía G, hay là lực hút nên ${{q}_{0}}<0$
${{F}_{03}}={{F}_{3}}\Rightarrow k\frac{\left| {{q}_{0}}q \right|}{{{\left( \frac{2}{3}a\frac{\sqrt{3}}{2} \right)}^{2}}}=\sqrt{3}k\frac{{{q}^{2}}}{{{a}^{2}}}\Rightarrow {{q}_{0}}=-\frac{\sqrt{3}}{3}q\approx 3,{{46.10}^{-7}}C$
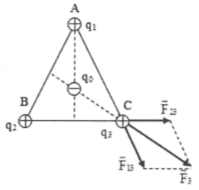
| Bài tập 14: Hai điện tích ${{q}_{1}}={{2.10}^{-8}}C,{{q}_{2}}=-{{8.10}^{-8}}C$ đặt tại A và B trong không khí. AB = 8cm. Một điện tích ${{q}_{3}}$ đặt tại C
a) C ở đâu để ${{q}_{3}}$ cân bằng b) Dấu và độ lớn của ${{q}_{3}}$ để ${{q}_{1}};{{q}_{2}}$ cũng cân bằng (Hệ điện tích cân bằng) |
Lời giải chi tiết
a) Để ${{q}_{3}}$cân bằng: $\overrightarrow{{{F}_{3}}}=\overrightarrow{{{F}_{13}}}+\overrightarrow{{{F}_{23}}}=\overrightarrow{0}\Rightarrow \overrightarrow{{{F}_{13}}}=-\overrightarrow{{{F}_{23}}}\Rightarrow $ điểm C phải thuộc AB
Vì ${{q}_{1}}>0,{{q}_{2}}<0$nên C nằm ngoài AB và gần phía A
Độ lớn ${{F}_{13}}={{F}_{23}}\Leftrightarrow k.\frac{\left| {{q}_{1}}{{q}_{3}} \right|}{C{{A}^{2}}}=k.\frac{\left| {{q}_{2}}{{q}_{3}} \right|}{C{{B}^{2}}}\Rightarrow \frac{CA}{CB}=\sqrt{\left| \frac{{{q}_{1}}}{{{q}_{2}}} \right|}=\frac{1}{2}\Rightarrow CB=2CA\left( 1 \right)$
Lại có: $CB-CA=AB=8cm\left( 2 \right)$
Từ (1) và (2) $\Rightarrow \left\{ \begin{array}{} CA=8cm \\ {} CB=16cm \\ \end{array} \right.;$ dấu và độ lớn của ${{q}_{3}}$ tùy ý
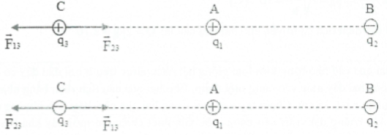
b) Để ${{q}_{1}}$cân bằng: $\overrightarrow{{{F}_{1}}}=\overrightarrow{{{F}_{21}}}+\overrightarrow{{{F}_{31}}}=\overrightarrow{0}\Rightarrow \overrightarrow{{{F}_{21}}}=-\overrightarrow{{{F}_{31}}}\Rightarrow \overrightarrow{{{F}_{21}}}\uparrow \downarrow \overrightarrow{{{F}_{31}}}\left( 3 \right)$
Vì ${{q}_{1}}>0,{{q}_{2}}<0$ nên $\overrightarrow{{{F}_{21}}}\uparrow \uparrow \overrightarrow{AB}\left( 4 \right)$
Lại có: $\overrightarrow{AC}\uparrow \downarrow \overrightarrow{AB}\left( 5 \right)$
Từ (3), (4), (5) suy ra $\Rightarrow \overrightarrow{{{F}_{31}}}\uparrow \uparrow \overrightarrow{AC}\Rightarrow {{q}_{1}}{{q}_{3}}<0\Rightarrow {{q}_{3}}<0$
Độ lớn: ${{F}_{31}}={{F}_{21}}\Leftrightarrow k\frac{\left| {{q}_{1}}{{q}_{3}} \right|}{A{{C}^{2}}}=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{A{{B}^{2}}}\Rightarrow \left| {{q}_{3}} \right|=\frac{A{{C}^{2}}}{A{{B}^{2}}}\left| {{q}_{2}} \right|\Rightarrow {{q}_{3}}=-{{8.10}^{-8}}C$
Vì $\left\{ \begin{array}{} \overrightarrow{{{F}_{13}}}+\overrightarrow{{{F}_{23}}}=\overrightarrow{0} \\ {} \overrightarrow{{{F}_{21}}}+\overrightarrow{{{F}_{31}}}=\overrightarrow{0} \\ \end{array} \right.\Rightarrow \overrightarrow{{{F}_{13}}}+\overrightarrow{{{F}_{23}}}+\overrightarrow{{{F}_{21}}}+\overrightarrow{{{F}_{31}}}=\overrightarrow{0}$
$\Rightarrow \overrightarrow{{{F}_{32}}}+\overrightarrow{{{F}_{12}}}=\overrightarrow{0}\Rightarrow $ điện tích ${{q}_{2}}$ cũng cân bằng

Chú ý: Nếu hệ gồm n điện tích có (n – 1) điện tích cân bằng thì hệ đó cân bằng
|
Bài tập 15: Hai qua cầu nhỏ giống nhau bằng kim loại có khối lượng m = 5 g. được treo vào cùng một điểm O bằng 2 sợi dây không dãn, dài 30 cm. Cho hai quả cầu tiếp xúc với nhau rồi tích điện cho mỗi quả cầu thì thấy chúng đẩy nhau cho đến khi 2 dây treo hợp với nhau 1 góc 90°. Tính điện tích mà ta đã truyền cho quả cầu. Lấy $g=10m/{{s}^{2}}$ |
Lời giải
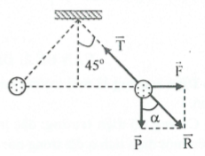
Các lực tác dụng lên quả câu gồm: trọng lực $\overrightarrow{P}$, lực căng dây $\overrightarrow{T}$ , lực tương tác tĩnh điện (lực tĩnh điện) $\overrightarrow{F}$ giữa hai quả cầu
Khi quả cầu cân bằng ta có: $\overrightarrow{T}+\overrightarrow{P}+\overrightarrow{F}=0\Leftrightarrow \overrightarrow{T}+\overrightarrow{R}=0$
$\Rightarrow \overrightarrow{R}$cùng phương, ngược chiều với $\overrightarrow{T}\Rightarrow \alpha =45{}^\circ $
Ta có: $\tan 45{}^\circ =\frac{F}{P}\Rightarrow F=P=mg=0,05N$
Mà $\left\{ \begin{array}{} F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}} \\ {} \left| {{q}_{1}} \right|=\left| {{q}_{2}} \right|=\left| q \right| \\ \end{array} \right.\Rightarrow F=k\frac{{{q}^{2}}}{{{r}^{2}}}$
Từ hình có: $r=2\left( \ell \sin 45{}^\circ \right)=\ell \sqrt{2}$
Do đó: $F=k\frac{{{q}^{2}}}{2{{\ell }^{2}}}\Rightarrow \left| q \right|=\ell \sqrt{\frac{2F}{k}}={{10}^{-6}}C$
Vậy tổng độ lớn điện tích đã truyền cho hai quả cầu là $Q=2\left| q \right|={{2.10}^{-6}}C$
|
Bài tập 16: Hai quả cầu nhỏ bằng kim loại giống hệt nhau được treo ở hai đầu dây có cùng chiều dài. Hai đầu kia của hai dây móc vào cùng một điểm. Cho hai quả cầu tích điện bằng nhau, lúc cân bằng chúng cách nhau r = 6,35 cm. Chạm tay vào một trong hai quả cầu, hãy tính khoảng cách r’ giữa hai quả cầu sau khi chúng đạt vị trí cân bằng mới. Giả thiết chiều dài mỗi dây khá lớn so với khoảng cách hai quả cầu lúc cân bằng. Lấy $\sqrt[3]{4}=1,5785$ |
Lời giải
Các lực tác dụng lên mỗi quả cầu gồm: trọng lực $\overrightarrow{P}$, lực tương tác tĩnh điện $\overrightarrow{F}$ và lực căng của dây treo $\overrightarrow{T}$
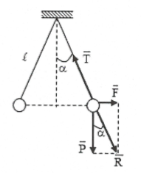
Khi quả cầu cân bằng thì: $\underbrace{\left( \overrightarrow{{{F}_{d}}}+\overrightarrow{P} \right)}_{\overrightarrow{R}}+\overrightarrow{T}=0\Leftrightarrow \overrightarrow{R}+\overrightarrow{T}=0$
$\Rightarrow \overrightarrow{R}$ có phương sợi dây $\Rightarrow \tan \alpha =\frac{F}{P}$
$\Rightarrow F=P\tan \alpha =P\frac{\frac{r}{2}}{\sqrt{{{\ell }^{2}}-{{\left( \frac{r}{2} \right)}^{2}}}}$
Nhận thấy: ${{\ell }^{2}}>>{{\left( \frac{r}{2} \right)}^{2}}\Rightarrow {{\ell }^{2}}-{{\left( \frac{r}{2} \right)}^{2}}\approx {{\ell }^{2}}\Rightarrow \sqrt{{{\ell }^{2}}-{{\left( \frac{r}{2} \right)}^{2}}}\approx \ell \Rightarrow F=\frac{\Pr }{2\ell }$
Lúc đầu: ${{F}_{1}}=k\frac{{{q}^{2}}}{{{r}^{2}}}=\frac{\Pr }{2\ell }\Rightarrow k\frac{{{q}^{2}}}{{{r}^{3}}}=\frac{P}{2\ell }\left( 1 \right)$
Giả sử ta chạm tay vào quả 1, kết quả sau đó quả cầu 1 sẽ mất điện tích, lúc đó giữa hai quả cầu không còn lực tương tác nên chúng sẽ trở về vị trị dây treo thẳng đứng. Khi chúng vừa chạm nhau thì điện tích của quả 2 sẽ truyền sang quả 1 và lúc này điện tích mỗi quả sẽ là:
$q_{1}^{‘}=q_{2}^{‘}=\frac{{{q}_{2}}}{2}=\frac{q}{2}\Rightarrow {{F}_{2}}=k\frac{{{q}^{2}}}{3{{\left( {{r}^{‘}} \right)}^{2}}}=\frac{\Pr ‘}{2\ell }\Rightarrow k\frac{{{q}^{2}}}{4{{\left( {{r}^{‘}} \right)}^{3}}}=\frac{P}{2\ell }\left( 2 \right)$
Từ (1) (2) ta có: $4{{\left( r’ \right)}^{3}}={{r}^{3}}\Rightarrow {{r}^{‘}}=\frac{r}{\sqrt[3]{4}}=4\left( cm \right)$
