VẤN ĐỀ 3: CÔNG CỦA LỰC ĐIỆN. THẾ NĂNG, ĐIỆN THẾ, HIỆU ĐIỆN THẾ
LÝ THUYẾT TRỌNG TÂM
– Công của lực điện: ${{A}_{MN}}=q.E.d\left( J \right)$ với $d=s.\cos \alpha $
+) A > 0: công phát động; A < 0: công cản
+) Công của lực điện tác dụng lên một điện tích không phụ thuộc vào dạng đường đi mà chỉ phụ thuộc vào vị trí điểm đầu và cuối của đường đi trong điện trường
– Thế năng: đặc trưng cho khả năng sinh công của điện trường
+) Trong điện trường đều: ${{W}_{M}}={{A}_{M}}=qE{{d}_{M}}$ với dM là khoảng cách từ M đến bản âm
+) Đối với điện trường của điện tích điểm: ${{W}_{M}}=q\left( k\frac{Q}{\varepsilon {{r}_{M}}} \right)\left( J \right)$
– Điện thế: ${{V}_{M}}=\frac{{{W}_{M}}}{q}=\frac{{{A}_{M\infty }}}{q}\left( V \right)$
+) Điện thế ${{V}_{M}}$ là một đại lượng đại số có thể âm, dương hoặc bằng 0.
+) Điện thế gây ra tại M bởi một điện tích điểm Q cách M khoảng r: ${{V}_{M}}=k\frac{Q}{\varepsilon {{r}_{M}}}\left( {{V}_{\infty }}=0 \right)$
– Hiệu điện thế: ${{U}_{MN}}={{V}_{M}}-{{V}_{N}}=\frac{{{W}_{M}}-{{W}_{N}}}{q}=\frac{{{A}_{MN}}}{q}\left( V \right)$
– Xét với điện trường đều: ${{U}_{MN}}=E.d$
– Liên hệ giữa công của lực điện và hiệu điện năng của điện tích:
${{A}_{MN}}={{W}_{M}}-{{W}_{N}}=q{{V}_{M}}-q{{V}_{N}}=q\left( {{V}_{M}}-{{V}_{N}} \right)=q.{{U}_{MN}}$
CÁC DẠNG BÀI TẬP
DẠNG 1: CÔNG LỰC ĐIỆN. THẾ NĂNG
BÀI TẬP LUYỆN TẬP DẠNG 1
|
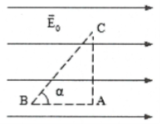
Bài tập 1: Một điện tích $q={{4.10}^{-8}}C$ di chuyển trong một điện trường đều có cường độ $E=100V/m$ theo một đường gấp khúc ABC, đoạn AB = 20cm và vecto độ dời $\overrightarrow{AB}$ làm với đường sức điện một góc $30{}^\circ .$ Đoạn BC dài 40cm và vecto độ dời $\overrightarrow{BC}$ làm với đường sức điện một góc $120{}^\circ $. Công của lực điện là: A. $-1,{{07.10}^{-7}}J$ B. $-1,{{51.10}^{-7}}J$ C. $1,{{07.10}^{-7}}J$ D. $-1,{{51.10}^{-7}}J$ |
Lời giải chi tiết
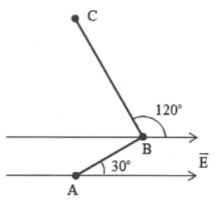
Từ hình ta có:
${{d}_{AB}}=AB\cos 30{}^\circ =20.\frac{\sqrt{3}}{2}=10\sqrt{3}cm$
${{d}_{BC}}=BC\cos 120{}^\circ =40.\frac{-1}{2}=-20cm$
Công của lực điện khi làm điện tích q di chuyển theo đường gấp khúc ABC là:
$A={{A}_{AB}}+{{A}_{BC}}=qE\left( {{d}_{AB}}+{{d}_{BC}} \right)$
$={{4.10}^{-8}}.100.\left[ 0,1\sqrt{3}+(-0,2) \right]=-1,{{07.10}^{-7}}\,\,J.$ Chọn A.
|
Bài tập 2: Người ta dịch chuyể điện tích $q={{4.10}^{-8}}C$ dọc theo các cạnh của tam giác ABC vuông tại A có cạnh AB = 6cm, AC = 8cm trong điện trường đều có cường độ E = 5000 V/m. Biết $\overrightarrow{E}//\overrightarrow{AC}$ . Tính công của lực điện trường dùng để dịch chuyển q dọc theo các cạnh AB, CB, AC. |
Lời giải chi tiết
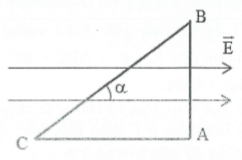
Công của lực điện trường di chuyển q:
${{A}_{AC}}=q.E.AC.\cos 180{}^\circ ={{4.10}^{-8}}.5000.0,08.\left( -1 \right)=-1,{{6.10}^{-5}}J$
${{A}_{AB}}=q.E.AB.\cos 90{}^\circ =0_{{}}^{{}}$
Điện tích di chuyển vuông góc với đường sức từ thì lực điện không thực hiện công.
$\begin{array}{} BC=\sqrt{{{6}^{2}}+{{8}^{2}}}=10cm=0,1m \\ {} \tan \alpha =\frac{6}{8}\Rightarrow \alpha \approx 37{}^\circ \\ {} {{A}_{BC}}=q.E.CB.cos37{}^\circ ={{4.10}^{-8}}.5000.0,1.0,8=1,{{6.10}^{-5}}J \\ \end{array}$
|
Bài tập 3: Một electron di chuyển một đoạn 6 cm, từ điểm M đến điểm N dọc theo một đường sức điện của điện trường đều thì lực sinh công $9,{{6.10}^{-18}}J$ . Tính công mà lực điện sinh ra khi electron di chuyển tiếp 4cm từ điểm N đến điểm P theo phương và chiều nói trên A. $9,{{6.10}^{-18}}J$ B. $6,{{4.10}^{-18}}J$ C. $12,{{8.10}^{-18}}J$ D. $8,{{6.10}^{-18}}J$ |
Lời giải chi tiết
Công của electron sinh ra khi electron di chuyển từ M đến N: ${{A}_{MN}}=qE{{d}_{MN}}$
Vì $A>0,E>0,q<0\Rightarrow {{d}_{MN}}<0\Rightarrow {{d}_{MN}}=-0,06m$
Þ electron đang di chuyển ngược chiều $\overrightarrow{E}\Rightarrow E=\frac{{{A}_{MN}}}{q{{d}_{MN}}}=\frac{9,{{6.10}^{-18}}}{\left( -1,{{6.10}^{-19}} \right)\left( -0,06 \right)}=1000V/m$
Þ Công mà electron di chuyển tiếp 4cm là
.
${{A}_{NP}}=qE{{d}_{NP}}=\left( -1,{{6.10}^{-19}} \right).1000.0,04.cos180{}^\circ =6,{{4.10}^{-18}}J$ . Chọn B.
|
Bài tập 4: Khi một điện tích q di chuyển trong một điện trường từ một điểm A có thế năng tĩnh điện 2,5J đến một điểm B thì lực điện sinh công 2,5J. Tính thế năng tĩnh điện của q tại B sẽ là A. -2,5 J B. -5 J C. 5 J D. 0 J |
Lời giải chi tiết
Công của lực điện ${{A}_{AB}}={{W}_{tA}}-{{W}_{tB}}\Leftrightarrow 2,5-{{W}_{tB}}=2,5J\Rightarrow {{W}_{tB}}=0J$ . Chọn D
|
Bài tập 5: Một electron bay ra từ bản âm sang bản dương của tụ điện phẳng. Điện trường giữa hai bản tụ có cường độ ${{9.10}^{4}}V/m$ . Khoảng cách giữa hai bản là d = 7,2cm. Khối lượng của e là $9,{{1.10}^{-31}}kg$ . Vận tốc đầu của electron là không. Vận tốc của electron khi tới bản dương của tụ điện là A. $4,{{77.10}^{7}}m/s$ B. $3,{{65.10}^{7}}m/s$ C. $4,{{01.10}^{6}}m/s$ D. $3,{{92.10}^{7}}m/s$ |
Lời giải chi tiết
Lực điện tác dụng lên điện tích $F=\left| e \right|E=1,{{6.10}^{-19}}{{.9.10}^{4}}=1,{{44.10}^{-14}}N$
Định luật II Niu-tơn có $F=ma\Rightarrow a=\frac{F}{m}=1,{{58.10}^{16}}m/{{s}^{2}}$
Áp dụng công thức độc lập thời gian ${{v}^{2}}-v_{0}^{2}=2as$
$\Rightarrow v=\sqrt{2as}=\sqrt{2.1,{{58.10}^{16}}.0,072}=4,{{77.10}^{7}}m/s$ .
Chọn A.
DẠNG 2: ĐIỆN THẾ. HIỆU ĐIỆN THẾ
BÀI TẬP LUYỆN TẬP DẠNG 2
|
Bài tập 6: Tam giác ABC vuông tại A được đặt trong điện trường đều $\overrightarrow{{{E}_{0}}};\alpha =ABC=60{}^\circ ,AB//\overrightarrow{{{E}_{0}}}.$ Biết BC = 6cm, ${{U}_{BC}}=120V$ . a) Tìm ${{U}_{AC}},{{U}_{BA}}$ và cường độ điện trường ${{E}_{0}}$ b) Đặt thêm ở C điện tích điểm $q={{9.10}^{-10}}C.$ Tìm cường độ điện trường ở A. |
Lời giải chi tiết
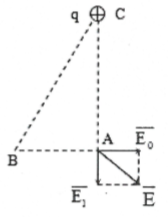
a) Hiệu điện thế giữa 2 điểm A, C: ${{U}_{AC}}={{E}_{0}}.AC.\cos 90{}^\circ =0$
(hình chiếu của AC lên đường sức bằng 0)
Hiệu điện thế giữa 2 điểm A, B:
${{U}_{BC}}={{E}_{0}}.BC.\cos 60{}^\circ ={{E}_{0}}.BA={{U}_{BA}}=120V$
Cường độ điện trường ${{E}_{0}}:$
${{E}_{0}}=\frac{{{U}_{BC}}}{BC.\cos 60{}^\circ }=\frac{120}{0,06.\cos 60{}^\circ }=4000V/m$
b) Điện trường tại A là tổng hợp điện trường đều $\overrightarrow{{{E}_{0}}}$ và điện trường gây ra bởi điện tích điểm q đặt tại C.
${{E}_{q}}=\frac{kq}{A{{C}^{2}}}=\frac{kq}{{{\left( BC\sin \alpha \right)}^{2}}}\Leftrightarrow {{E}_{q}}=\frac{{{9.10}^{9}}{{.9.10}^{-10}}}{{{\left( 0,06.\sin 60{}^\circ \right)}^{2}}}=3000V/m$
Cường độ điện trường tổng hợp tại A: $\overrightarrow{E}=\overrightarrow{{{E}_{0}}}+\overrightarrow{{{E}_{q}}}$
Vì $\overrightarrow{{{E}_{q}}}\bot \overrightarrow{{{E}_{0}}}\Rightarrow E=\sqrt{E_{0}^{2}+E_{q}^{2}}=\sqrt{{{3000}^{2}}+{{4000}^{2}}}=5000V/m$
|
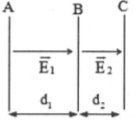
Bài tập 7: Có ba bản kim loại phẳng A, B, C đặt song song như hình vẽ. Cho ${{d}_{1}}=5cm,{{d}_{2}}=4cm$ , bản C nối đất, bản A, B được tích điện có điện thế lần lượt là -100V, +50V. Điện trường giữa các bản là điện trường đều. Xác định các vecto cường độ điện trường $\overrightarrow{{{E}_{1}}},\overrightarrow{{{E}_{2}}}$ |
Lời giải chi tiết
Chọn bản C làm gốc ${{V}_{C}}=0$
${{E}_{2}}=\frac{{{U}_{BC}}}{{{d}_{2}}}=\frac{{{V}_{B}}-{{V}_{C}}}{{{d}_{2}}}=\frac{{{V}_{B}}}{{{d}_{2}}}=\frac{50}{0,04}=1250V/m$
$\overrightarrow{{{E}_{2}}}$ hướng từ bản B sang bản C
${{E}_{1}}=\frac{{{U}_{BA}}}{{{d}_{1}}}=\frac{{{V}_{B}}-{{V}_{A}}}{{{d}_{1}}}=\frac{50-\left( -100 \right)}{0,05}=3000V/m$
|
Bài tập 8: Tìm hiệu điện thế giữa hai vị trí M, N trong không khí. Biết rằng điện tích điểm $q={{3.10}^{-9}}C$ dịch chuyển từ M đến N thu được năng lượng $W={{6.10}^{-7}}J$ |
Lời giải chi tiết
Năng lượng W bằng công của lực điện trường: $W={{A}_{MN}}=q{{U}_{MN}}\Rightarrow {{U}_{MN}}=\frac{W}{q}=200V$
|
Bài tập 9: Điện tích $Q={{5.10}^{-9}}C$ đặt ở O trong không khí. a) Cần thực hiện một công ${{A}_{1}}$ bao nhiêu để đưa điện tích $q={{4.10}^{-8}}C$ từ M (cách Q đoạn ${{r}_{1}}=40cm$) đến N (cách Q đoạn ${{r}_{2}}=25cm$) b) Cần thực hiện một công ${{A}_{2}}$ bao nhiêu để đưa q từ M chuyển động chậm dần ra xa vô cùng. |
Lời giải chi tiết
a) Điện thế tại M do Q gây ra là: ${{V}_{M}}=\frac{kQ}{{{r}_{M}}}=\frac{{{9.10}^{9}}{{.5.10}^{-9}}}{0,4}=112,5V$
Điện thế tại N do Q gây ra là: ${{V}_{N}}=\frac{kQ}{{{r}_{N}}}=\frac{{{9.10}^{9}}{{.5.10}^{-9}}}{0,25}=180V$
Khi di chuyển q từ M đến N, lực điện (do điện trường của điện tích Q gây ra) đã thực hiện một công:
$A=q\left( {{V}_{M}}-{{V}_{N}} \right)={{4.10}^{-8}}.\left( 112,5-180 \right)=-2,{{7.10}^{-6}}J$
Công cần thiết để di chuyển q từ M đến N là: ${{A}_{1}}=-A=2,{{7.10}^{-6}}J$
b) Điện thế tại M do Q gây ra là: ${{V}_{M}}=\frac{kQ}{{{r}_{M}}}=\frac{{{9.10}^{9}}{{.5.10}^{-9}}}{0,4}=112,5V$
Điện thế tại vô cùng bằng 0
Khi di chuyển q từ M ra vô cùng, lực điện (do điện trường của điện tích Q gây ra) đã thực hiện một công:
$A=q\left( {{V}_{M}}-{{V}_{\infty }} \right)={{4.10}^{-8}}\left( 112,5-0 \right)={{45.10}^{-7}}J$
Để di chuyển q từ M ra vô cùng chậm dần thì phải có ngoại lực ngược chiều lực điện do đó công cần thiết để di chuyển từ M ra vô cùng là: ${{A}_{2}}=-A=-{{45.10}^{-7}}J$
|
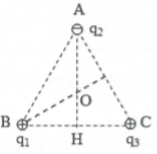
Bài tập 10: Có 3 điện tích điểm ${{q}_{1}}={{15.10}^{-9}}C,{{q}_{2}}=-{{12.10}^{-9}}C,{{q}_{3}}={{7.10}^{-9}}C,$ đặt tại ba đỉnh của tam giác đều ABC, cạnh 10cm (hình vẽ) a) Tính điện thế tại trong tâm O của tam giác b) H là trung điểm của BC. Tính hiệu điện thế ${{U}_{OH}}$ c) Tính công cần thiết để electron chuyển động từ O đến H |
Lời giải chi tiết
Ta có: $HB=HC=5cm=0,05m$
$AH=\sqrt{{{10}^{2}}-{{5}^{2}}}=5\sqrt{3}cm=0,05\sqrt{3}m$
Vì tam giác ABC đều $\Rightarrow OA=OB=OC=\frac{2}{3}AH=\frac{2}{3}.\sqrt{{{10}^{2}}-{{5}^{2}}}=\frac{10}{\sqrt{3}}cm=\frac{0,1}{\sqrt{3}}m$
a) Điện thế tại O là ${{V}_{O}}={{V}_{1O}}+{{V}_{2O}}+{{V}_{3O}}=\frac{k{{q}_{1}}}{OA}+\frac{k{{q}_{2}}}{OB}+\frac{k{{q}_{3}}}{OC}$
$\Rightarrow {{V}_{O}}={{9.10}^{9}}.\frac{\sqrt{3}}{0,1}.\left( {{15.10}^{-9}}-{{12.10}^{-9}}+{{7.10}^{-9}} \right)=1558,8V$
b) Điện thế tại H là ${{V}_{H}}={{V}_{1H}}+{{V}_{2H}}+{{V}_{3H}}=\frac{k{{q}_{1}}}{BH}+\frac{k{{q}_{2}}}{AH}+\frac{k{{q}_{3}}}{CH}$
$\Rightarrow {{V}_{H}}={{9.10}^{9}}.\left( \frac{{{15.10}^{-9}}}{0,05}-\frac{{{12.10}^{-9}}}{0,05\sqrt{3}}+\frac{{{7.10}^{-9}}}{0,05} \right)=658,8V$
$\Rightarrow {{U}_{OH}}={{V}_{O}}-{{V}_{H}}=1558,8-658,8=900V$
c) Công cần thiết để electron chuyển động từ O đến H là:
${{A}_{OH}}=e.{{U}_{OH}}=-1,{{6.10}^{-19}}.900=-1,{{44.10}^{-16}}J$
|
Bài tập 11: Hai điện tích điểm ${{q}_{1}}={{10}^{-9}},{{q}_{2}}={{4.10}^{-9}}C$ đặt cách nhau a = 9cm trong chân không. Tính điện thế tại điểm mà tại đó cường độ điện trường tổng hợp bằng 0 |
Lời giải chi tiết
Gọi $\overrightarrow{{{E}_{1}}},\overrightarrow{{{E}_{2}}}$ là vecto cường độ điện trường do điện tích ${{q}_{1}},{{q}_{2}}$ gây ra
Theo nguyên lí chồng chất điện trường: $\overrightarrow{{{E}_{C}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}$
Tại điểm C có $\overrightarrow{{{E}_{C}}}=0$ nên $\overrightarrow{{{E}_{1}}}=-\overrightarrow{{{E}_{2}}}$ Þ Điểm C phải nằm trong đoạn nối hai điện tích
Gọi khoảng cách từ C tới hai điện tích ${{q}_{1}},{{q}_{2}}$ lần lượt là ${{r}_{1}},{{r}_{2}}$
$\Rightarrow \frac{k{{q}_{1}}}{r_{1}^{2}}=\frac{k{{q}_{2}}}{r_{2}^{2}}\Rightarrow \frac{r_{2}^{2}}{r_{1}^{2}}=\frac{{{q}_{2}}}{{{q}_{1}}}=4\Rightarrow {{r}_{2}}=2{{r}_{1}}\left( 1 \right)$
Mà ${{r}_{2}}+{{r}_{1}}=9\left( 2 \right)$
Từ (1) và (2) $\Rightarrow {{r}_{1}}=3cm,{{r}_{2}}=6cm$
Þ Điện thế tại C là ${{V}_{C}}=k\left( \frac{{{q}_{1}}}{{{r}_{1}}}+\frac{{{q}_{2}}}{{{r}_{2}}} \right)={{9.10}^{9}}.\left( \frac{-{{10}^{-9}}}{0,03}+\frac{{{4.10}^{-9}}}{0,06} \right)=900V$
|
Bài tập 12: Hai quả cầu kim loại bán kính R1, R2 lần lượt được tích các điện tích ${{q}_{1}},{{q}_{2}}$ và đặt ở hai nơi xa nhau trong không khí. Điện thế của mỗi quả cầu là V1, V2. Hỏi khi nối hai quả cầu bằng dây dẫn, electron sẽ chuyển động từ quả cầu nào sang quả cầu nào? Xét các trường hợp: a) ${{R}_{1}}>{{R}_{2}};{{q}_{1}}={{q}_{2}}>0$ b) ${{R}_{1}}>{{R}_{2}};{{V}_{1}}={{V}_{2}}$ . So sánh ${{q}_{1}},{{q}_{2}}$ c) ${{q}_{1}}>0,{{q}_{2}}<0$ |
Lời giải chi tiết
Quả cầu cô lập là 1 vật đẳng thế, điện tích sẽ nằm ở bề mặt quả cầu. Điện thế của quả cầu là $V=k\frac{q}{R}$
Khi nối hai quả cầu bằng dây dẫn, các điện tích sẽ di chuyển từ quả cầu này sang quả cầu kia nếu điện thế 2 quả cầu khác nhau. Electron mang điện tích âm sẽ di chuyển từ quả cầu có điện thế thấp đến quả cầu có điện thế cao.
a) Trường hợp 1: ${{R}_{1}}>{{R}_{2}};{{q}_{1}}={{q}_{2}}>0$
Điện thế: ${{V}_{1}}=k\frac{{{q}_{1}}}{{{R}_{1}}}<{{V}_{2}}=k\frac{{{q}_{2}}}{{{R}_{2}}}$: Electron sẽ di chuyển từ quả cầu (I) sang quả cầu (II)
b) Trường hợp 2: ${{R}_{1}}>{{R}_{2}};{{V}_{1}}={{V}_{2}}$
Điện thế: ${{V}_{1}}={{V}_{2}}\Leftrightarrow k\frac{{{q}_{1}}}{{{R}_{1}}}=k\frac{{{q}_{2}}}{{{R}_{2}}}:$ Các electron không di chuyển
Điện tích ${{q}_{1}};{{q}_{2}}$ cùng dấu và $\left| {{q}_{1}} \right|>\left| {{q}_{2}} \right|$
c) Trường hợp 3: ${{q}_{1}}>0,{{q}_{2}}<0$
Điện thế quả cầu I: ${{V}_{1}}=k\frac{{{q}_{1}}}{{{R}_{1}}}>0$
Điện thế quả cầu II: ${{V}_{2}}=k\frac{{{q}_{2}}}{{{R}_{2}}}<0$
Vì ${{V}_{1}}>{{V}_{2}}$ nên electron di chuyển từ quả cầu (II) sang quả cầu (I)
Chú ý: Các electron sẽ di chuyển cho đến khi nào điện thế 2 quả cầu bằng nhau thì ngừng, không di chuyển nữa.