Ứng dụng tích phân tính diện tích mặt phẳng– Công thức Các dạng bài tập và lý thuyết
1) Công thức tính diện tích của hình phẳng giới hạn bởi hai đồ thị hàm số
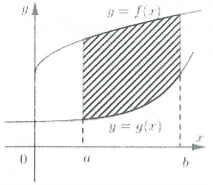
Cho hai đồ thị của hai hàm số $y=f\left( x \right),y=g\left( x \right)$ liên tục trên đoạn $\left[ a;b \right]$ và hai đường thẳng $x=a;x=b\left( a<b \right)$. Khi đó hình phẳng giới hạn bởi bốn đường $y=f\left( x \right),y=g\left( x \right)$ và hai đường thẳng $x=a;x=b$ có diện tích S được tính theo công thức: $S=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|d\text{x}}$.
Đặc biệt: Trong trường hợp $g\left( x \right)$ là trục hoành ($g\left( x \right)=0$) ta được công thức tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số $y=f\left( x \right)$, trục hoành và hai đường thẳng $x=a,x=b$ là:
$S=\int\limits_{a}^{b}{\left| f(x) \right|d\text{x}}$ (1).
Để tính diện tích S ta phải tính tích phân (1), muốn vậy ta phải phá dấu giá trị tuyệt đối:
Nếu $f\left( x \right)\ge 0,\forall x\in \left[ a;b \right]$ thì $S=\int\limits_{a}^{b}{\left| f\left( x \right) \right|d\text{x}}=\int\limits_{a}^{b}{f\left( x \right)d\text{x}}$.
Nếu $f\left( x \right)\le 0,\forall x\in \left[ a;b \right]$ thì $S=\int\limits_{a}^{b}{\left| f\left( x \right) \right|d\text{x}}=\int\limits_{a}^{b}{\left( -f\left( x \right) \right)d\text{x}}$.
Muốn xét dấu của biểu thức $f\left( x \right)$ ta thường có một số cách làm như sau:
@ Cách 1: Sử dụng bảng xét dấu cho $f\left( x \right)$ với ghi nhớ qua nghiệm bội lẻ $f\left( x \right)$ đổi dấu, qua nghiệm bội chẵn $f\left( x \right)$ không đổi dấu.
@ Cách 2: Dựa vào đồ thị của hàm số $y=f\left( x \right)$ trên đoạn $\left[ a;b \right]$ để suy ra dấu của $f\left( x \right)$ trên đoạn đó:
– Nếu trên đoạn $\left[ a;b \right]$ đồ thị hàm số $y=f\left( x \right)$ nằm phía trên trục hoành thì $f\left( x \right)\ge 0,\forall x\in \left[ a;b \right]$.
– Nếu trên đoạn $\left[ a;b \right]$ đồ thị hàm số $y=f\left( x \right)$ nằm phía dưới trục hoành thì $f\left( x \right)\le 0,\forall x\in \left[ a;b \right]$.
@ Cách 3: Nếu $f\left( x \right)$ không đổi dấu trên $\left[ a;b \right]$ thì ta có: $S=\int\limits_{a}^{b}{\left| f\left( x \right) \right|d\text{x}}=\left| \int\limits_{a}^{b}{f\left( x \right)dx} \right|$.
@ Cách 4: Sử dụng máy tính CASIO, tuy nhiên xu hướng ra đề thi THPT Quốc gia sẽ hạn chế CASIO nên cần chú ý cách giải tổng quát và hiểu rõ bản chất!
Chú ý:
– Khi tính diện tích của hình phẳng giới hạn bởi hai đồ thị hàm số ta có:
$S=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|d\text{x}}=\int\limits_{a}^{b}{\left| h\left( x \right) \right|d\text{x}}$ ta làm hoàn toàn tương tự như trên.
– Nếu đề bài không cho các đường thẳng giới hạn $x=a;x=b$ ta giải phương trình $f\left( x \right)=g\left( x \right)$ (hoặc $f\left( x \right)=0$ trong trường hợp $g\left( x \right)$ là trục hoành) để tìm cận của tích phân.
2) Ứng dụng tính diện tích hình tròn và hình Elip
a) Tính diện tích hình tròn
Trong hệ tọa độ Oxy cho đường tròn có phương trình: ${{x}^{2}}+{{y}^{2}}={{r}^{2}}\left( r>0 \right)$. Khi đó hình tròn đó có diện tích là: $S=\pi {{r}^{2}}$.
Ta có ${{x}^{2}}+{{y}^{2}}={{r}^{2}}\Leftrightarrow y=\pm \sqrt{{{r}^{2}}-{{x}^{2}}}$
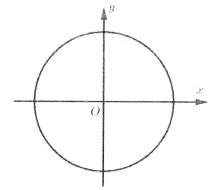
Với $y\ge 0$, ta có: $y=\sqrt{{{r}^{2}}-{{x}^{2}}}$ có đồ thị là nửa đường tròn phía trên trục hoành.
Bằng cách đặt $x=r\sin t$ ta có diện tích ${{S}_{1}}=\int\limits_{-r}^{r}{\sqrt{{{r}^{2}}-{{x}^{2}}}dx}=2\int\limits_{0}^{r}{\sqrt{{{r}^{2}}-{{x}^{2}}}dx}=\frac{\pi {{r}^{2}}}{2}$.
Do đó $S=2{{\text{S}}_{1}}=\pi {{r}^{2}}$.
b) Tính diện tích hình Elip
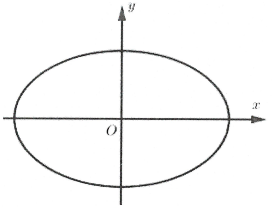
Trong hệ tọa độ Oxy cho elip có phương trình: $\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1,0<b<a$.
Chứng minh tương tự ta có diện tích của elip là: $S=\pi ab$ (đvdt).