Sự tương giao của đồ thị hàm số bậc 4 trùng phương – Cách giải bài tập có đáp án
Phương pháp giải bài toán tương giao của hàm bậc 4 trùng phương.
Xét sự tương giao đồ thị $\left( C \right):y=a{{x}^{4}}+b{{x}^{2}}+c\left( a\ne 0 \right)$ và trục hoành có phương trình $y=0$
Phương trình hoành độ giao điểm $\left( C \right)$ và trục hoành là $a{{x}^{4}}+b{{x}^{2}}+c=0\left( 1 \right)$
Bài toán liên quan đến số giao điểm
Số giao điểm của đồ thị $\left( C \right)$ và trục hoành chính là số nghiệm của phương trình (1).
Đặt $t={{x}^{2}}\ge 0$ thì (1) thành $a{{t}^{2}}+bt+c=0(2)$
+) $\left( C \right)$ cắt trục hoành tại 4 điểm phân biệt $\Leftrightarrow (2)$ có 2 nghiệm dương phân biệt
$\Leftrightarrow \left\{ \begin{array} {} \Delta ={{b}^{2}}-4ac>0 \\ {} {{t}_{1}}+{{t}_{2}}=-\frac{b}{a}>0 \\ {} {{t}_{1}}.{{t}_{2}}=\frac{c}{a}>0 \\ \end{array} \right.$
+) $\left( C \right)$ cắt trục hoành tại đúng 3 điểm phân biệt $\Leftrightarrow (2)$ có 1 nghiệm dương và 1 nghiệm bằng 0.
$\left( C \right)$ cắt trục hoành tại đúng 2 điểm phân biệt $\Leftrightarrow (2)$có nghiệm kép dương hoặc (2) có hai nghiệm trái dấu.
+) $\left( C \right)$ cắt trục hoành tại điểm duy nhất $\Leftrightarrow (2)$có nghiệm kép bằng 0 hoặc (2) có một nghiệm bằng 0 hoặc một nghiệm âm.
+) $\left( C \right)$ không cắt trục hoành $\Leftrightarrow (2)$ vô nghiệm, có nghiệm kép âm hoặc có 2 nghiệm phân biệt đều âm
Một số bài toán có thể thay trục hoành thành $d:y=m$ hoặc $(P):y=m{{x}^{2}}+n$ , phương pháp giải hoàn toàn tương tự như trên.
Bài toán liên quan đến tính chất giao điểm
Tìm điều kiện để $(C):y=a{{x}^{4}}+b{{x}^{2}}+c\left( a\ne 0 \right)$ cắt trục hoành tại bốn điểm phân biệt A, B, C, D thỏa mãn điều kiện cho trước.
Bước 1: Tìm điều kiện để (1) có 4 nghiệm phân biệt
$\Leftrightarrow (2)$ có 2 nghiệm dương phân biệt ${{t}_{1}}$ và ${{t}_{2}}$ $\Leftrightarrow \left\{ \begin{array} {} \Delta ={{b}^{2}}-4ac>0 \\ {} {{t}_{1}}+{{t}_{2}}=-\frac{b}{a}>0 \\ {} {{t}_{1}}.{{t}_{2}}=\frac{c}{a}>0 \\ \end{array} \right.$ (*)
Bước 2: Giả sử ${{t}_{1}}>{{t}_{2}}>0$ khi đó các nghiệm của (1) sắp xếp theo thứ tự tăng dần là $-\sqrt{{{t}_{1}}};-\sqrt{{{t}_{2}}};\sqrt{{{t}_{2}}};\sqrt{{{t}_{1}}}$, xử lý điều kiện và tìm giá trị của tham số.
Đặc biệt: Khi hoành độ 4 điểm A, B, C, D lập thành cấp số cộng hoặc $AB=BC=CD$ khi: $\sqrt{{{t}_{1}}}-\sqrt{{{t}_{2}}}=2\sqrt{{{t}_{2}}}\Leftrightarrow \sqrt{{{t}_{1}}}=3\sqrt{{{t}_{2}}}\Leftrightarrow {{t}_{1}}=9{{t}_{2}}$
Bài tập trắc nghiệm tương giao của hàm bậc 4, hàm trùng phương có đáp án chi tiết
| Bài tập 1: Số giá trị nguyên của tham số m để đồ thị hàm số $y={{x}^{4}}-8{{x}^{2}}+5-2m$ cắt trục hoành tại 4 điểm phân biệt là:
A. 9 B. 6 C. 7 D. 8 |
Lời giải chi tiết
Phương trình hoành độ giao điểm là ${{x}^{4}}-8{{x}^{2}}+5-2m=0$
Đặt $t={{x}^{2}},t\ge 0\Rightarrow PT\Leftrightarrow {{t}^{2}}-8t+5-2m=0\left( * \right)$
Phương trình ban đầu có 4 nghiệm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt thỏa mãn ${{t}_{1}}>{{t}_{2}}>0$
Khi đó $\left\{ \begin{array} {} {\Delta }'(*)>0 \\ {} {{t}_{1}}+{{t}_{2}}>0 \\ {} {{t}_{1}}.{{t}_{2}}>0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} 16-(5-2m)>0 \\ {} 8>0 \\ {} 5-2m>0 \\ \end{array} \right.\Leftrightarrow -\frac{11}{2}<m<\frac{5}{2}$
Kết hợp $m\in \mathbb{Z}\Rightarrow $ Có 8 giá trị của m. Chọn D.
| Bài tập 2: Cho hàm số $y={{x}^{4}}+2\left( m-2 \right){{x}^{2}}+4$ có đồ thị $\left( {{C}_{m}} \right)$ , với m là tham số thực. Tìm tập hợp T gồm tất cả các giá trị của tham số m để $\left( {{C}_{m}} \right)$ cắt Ox tại bốn điểm phân biệt
A. $T=\left( 0;2 \right)$ B. $T=\left( 4;+\infty \right)$ C. $T=\left( -\infty ;0 \right)\cup \left( 4;+\infty \right)$ D. $T=\left( -\infty ;0 \right)$ |
Lời giải chi tiết
Phương trình hoành độ giao điểm là ${{x}^{4}}+2\left( m-2 \right){{x}^{2}}+4=0\xrightarrow{t={{x}^{2}}}{{t}^{2}}+2\left( m-2 \right)t+4=0(*)$
Đồ thị hàm số và trục hoành có 4 giao điểm khi và chỉ khi PT hoành độ giáo điểm có 4 nghiệm phân biệt
$\Leftrightarrow (*)$ có hai nghiệm phân biệt $t>0\Rightarrow \left\{ \begin{array} {} {\Delta }'(*)>0 \\ {} {{t}_{1}}+{{t}_{2}}>0 \\ {} {{t}_{1}}.{{t}_{2}}>0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} {{\left( m-2 \right)}^{2}}-4>0 \\ {} -2(m-2)>0 \\ {} 4>0 \\ \end{array} \right.$
$\Rightarrow m<0\Rightarrow T=\left( -\infty ;0 \right)$ . Chọn D.
| Bài tập 3: Cho hàm số $y={{x}^{4}}-2m{{x}^{2}}+m+1\left( C \right)$. Gọi S là tập hợp các giá trị của m để $\left( C \right)$ cắt trục Ox tại 4 điểm phân biệt có hoành độ ${{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}$ thỏa mãn $x_{1}^{4}+x_{2}^{4}+x_{3}^{4}+x_{4}^{4}=20$. Tổng các phần tử của tập hợp (S) là:
A. 1 B. – 1 C. 2 D. – 3 |
Lời giải chi tiết
Phương trình hoành độ giao điểm của $\left( C \right)$ và Ox là ${{x}^{4}}-2m{{x}^{2}}+m+1=0\left( 1 \right)$
Đặt $t={{x}^{2}}:\left( 1 \right)\Rightarrow {{t}^{2}}-2mt+m+1=0\left( 2 \right)$
Để $\left( C \right)$ cắt trục Ox tại 4 điểm phân biệt $\Leftrightarrow (2)$ có 2 nghiệm phân biệt ${{t}_{1}}>{{t}_{2}}>0$
$\Leftrightarrow \left\{ \begin{array} {} {\Delta }’={{m}^{2}}-m-1>0 \\ {} S=2m>0 \\ {} P=m+1>0 \\ \end{array} \right.\left( * \right)$ . Theo Viet: $\left\{ \begin{array} {} {{t}_{1}}+{{t}_{2}}=2m \\ {} {{t}_{1}}.{{t}_{2}}=m+1 \\ \end{array} \right.$
Khi đó phương trình (1) có 4 nghiệm $-\sqrt{{{t}_{1}}};-\sqrt{{{t}_{2}}};\sqrt{{{t}_{2}}};\sqrt{{{t}_{1}}}$
Ta có: giả thiết bài toán $\Leftrightarrow t_{1}^{2}+t_{2}^{2}+t_{2}^{2}+t_{1}^{2}=20\Leftrightarrow t_{1}^{2}+t_{2}^{2}=10\Leftrightarrow {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-2{{t}_{1}}{{t}_{2}}=10$
$\Leftrightarrow 4{{m}^{2}}-2m-2=10\Leftrightarrow 2{{m}^{2}}-m-6=0\Leftrightarrow \left[ \begin{array} {} m=2 \\ {} m=-3 \\ \end{array} \right.$
Kết hợp (*) $\Rightarrow m=2$ là giá trị cần tìm. Chọn C.
| Bài tập 4: Cho hàm số $y={{x}^{4}}-(2m+1){{x}^{2}}+2\left( C \right)$. Gọi S là tập hợp các giá trị của m để $\left( C \right)$ cắt trục Ox tại 4 điểm phân biệt có hoành độ ${{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}$ thỏa mãn $\frac{1}{x_{1}^{4}}+\frac{1}{x_{2}^{4}}+\frac{1}{x_{3}^{4}}+\frac{1}{x_{4}^{4}}=\frac{5}{2}$
Số phần tử của tập hợp S là: A. 0 B. 1 C. 2 D. 3 |
Lời giải chi tiết
Phương trình hoành độ giao điểm của $\left( C \right)$ và Ox là ${{x}^{4}}-(2m+1){{x}^{2}}+2=0\left( 1 \right)$
Đặt $t={{x}^{2}}:\left( 1 \right)\Rightarrow {{t}^{2}}-(2m+1)t+2=0\left( 2 \right)$
Để $\left( C \right)$ cắt trục Ox tại 4 điểm phân biệt $\Leftrightarrow (2)$ có 2 nghiệm phân biệt ${{t}_{1}}>{{t}_{2}}>0$
$\Leftrightarrow \left\{ \begin{array} {} \Delta ={{\left( 2m+1 \right)}^{2}}-8>0 \\ {} S=2m+1>0 \\ {} P=2>0 \\ \end{array} \right.\left( * \right)$ . Theo Viet: $\left\{ \begin{array} {} {{t}_{1}}+{{t}_{2}}=2m+1 \\ {} {{t}_{1}}.{{t}_{2}}=2 \\ \end{array} \right.$
+) Khi đó phương trình (1) có 4 nghiệm $-\sqrt{{{t}_{1}}};-\sqrt{{{t}_{2}}};\sqrt{{{t}_{2}}};\sqrt{{{t}_{1}}}$ ta có: $\frac{1}{t_{1}^{2}}+\frac{1}{t_{2}^{2}}+\frac{1}{t_{3}^{2}}+\frac{1}{t_{4}^{2}}=\frac{5}{2}$
$\Leftrightarrow \frac{2}{t_{1}^{2}}+\frac{2}{t_{2}^{2}}=\frac{5}{2}\Leftrightarrow \frac{2\left( t_{1}^{2}+t_{2}^{2} \right)}{t_{1}^{2}.t_{2}^{2}}=\frac{5}{2}\Leftrightarrow t_{1}^{2}+t_{2}^{2}=5\Leftrightarrow {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-2{{t}_{1}}{{t}_{2}}=5\Leftrightarrow {{\left( 2m+1 \right)}^{2}}=9\Leftrightarrow \left[ \begin{array} {} m=1 \\ {} m=-2 \\ \end{array} \right.$
Kết hợp (*) $\Rightarrow m=1$ là giá trị cần tìm. Chọn B.
| Bài tập 5: Cho hàm số: $y={{x}^{4}}-2m{{x}^{2}}+m+4\left( C \right)$. Gọi S là tập hợp các giá trị của m để $\left( C \right)$ cắt Ox tại 4 điểm phân biệt có hoành độ ${{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}$ thỏa mãn: $\left| {{x}_{1}} \right|+\left| {{x}_{2}} \right|+\left| {{x}_{3}} \right|+\left| {{x}_{4}} \right|=8$ . Tổng các phần tử của tập hợp S là:
A. 5 B. 12 C. 17 D. – 17 |
Lời giải chi tiết
Phương trình hoành độ giao điểm của $\left( C \right)$ và Ox là ${{x}^{4}}-2m{{x}^{2}}+m+4=0\left( 1 \right)$
Đặt $t={{x}^{2}}:\left( 1 \right)\Rightarrow {{t}^{2}}-2mt+m+4=0\left( 2 \right)$
Để $\left( C \right)$ cắt trục Ox tại 4 điểm phân biệt $\Leftrightarrow (2)$ có 2 nghiệm phân biệt ${{t}_{1}}>{{t}_{2}}>0$
$\Leftrightarrow \left\{ \begin{array} {} {\Delta }’={{m}^{2}}-m-4>0 \\ {} S=2m>0 \\ {} P=m+4>0 \\ \end{array} \right.\left( * \right)$ . Theo Viet: $\left\{ \begin{array} {} {{t}_{1}}+{{t}_{2}}=2m \\ {} {{t}_{1}}.{{t}_{2}}=m+4 \\ \end{array} \right.$
+) Khi đó phương trình (1) có 4 nghiệm $-\sqrt{{{t}_{1}}};-\sqrt{{{t}_{2}}};\sqrt{{{t}_{2}}};\sqrt{{{t}_{1}}}$
Ta có: giả thiết $\Leftrightarrow \left| -\sqrt{{{t}_{1}}} \right|+\left| -\sqrt{{{t}_{2}}} \right|+\left| \sqrt{{{t}_{2}}} \right|+\left| \sqrt{{{t}_{1}}} \right|=8\Leftrightarrow 2\left( \sqrt{{{t}_{1}}}+\sqrt{{{t}_{2}}} \right)=8\Leftrightarrow \sqrt{{{t}_{1}}}+\sqrt{{{t}_{2}}}=4$
$\Leftrightarrow {{t}_{1}}+{{t}_{2}}+2\sqrt{{{t}_{1}}{{t}_{2}}}=16\Leftrightarrow 2\sqrt{m+4}=16-2m\Leftrightarrow \sqrt{m+4}=8-m\Leftrightarrow \left\{ \begin{array} {} m\le 8 \\ {} {{m}^{2}}-17m+60=0 \\ \end{array} \right.\Leftrightarrow m=5$
Vậy m = 5 là giá trị cần tìm. Chọn A.
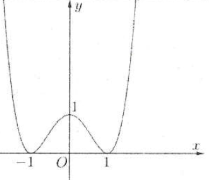
| Bài tập 6: Cho hàm số $y=f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c$ có đồ thị như hình vẽ. Tập hợp các giá trị thực của m để đường thẳng $d:y=-m+2$ cắt đồ thị hàm số $y=f\left( x \right)$ tại bốn điểm phân biệt cách đều nhau là
A. $\left\{ \frac{34}{25};\frac{7}{4} \right\}$ B. $\left\{ \frac{34}{25} \right\}$ C. $\left\{ \frac{7}{4} \right\}$ D. $\left\{ 1;2 \right\}$ |
Lời giải chi tiết
Dựa vào đồ thị hàm số, suy ra $y=f\left( x \right)={{x}^{4}}-2{{x}^{2}}+1$
PT hoành độ giao điểm hai đồ thị là ${{x}^{4}}-2{{x}^{2}}+1=-m+2\xrightarrow{t={{x}^{2}}}{{t}^{2}}-2t+m-1=0\left( * \right)$
Hai đồ thị có 4 giao điểm khi và chỉ khi PT (*) có hai nghiệm dương phân biệt
Suy ra $\Leftrightarrow \left\{ \begin{array} {} {\Delta }'(*)>0 \\ {} {{t}_{1}}+{{t}_{2}}>0 \\ {} {{t}_{1}}.{{t}_{2}}>0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} 1-m+1>0 \\ {} 2>0 \\ {} m-1>0 \\ \end{array} \right.\Leftrightarrow 1<m{{t}_{2}}$, 4 nghiệm của PT ban đầu theo thứ tự từ bé đến lớn sẽ là $-\sqrt{{{t}_{1}}};-\sqrt{{{t}_{2}}};\sqrt{{{t}_{2}}};\sqrt{{{t}_{1}}}$
Theo đề bài ta có $-\sqrt{{{t}_{1}}}+\sqrt{{{t}_{2}}}=-2\sqrt{{{t}_{2}}}\Rightarrow \sqrt{{{t}_{1}}}=3\sqrt{{{t}_{2}}}\Leftrightarrow {{t}_{1}}=9{{t}_{2}}\Rightarrow \left\{ \begin{array} {} {{t}_{1}}+{{t}_{2}}=2 \\ {} {{t}_{1}}.{{t}_{2}}=m-1 \\ {} {{t}_{1}}=9{{t}_{2}} \\ \end{array} \right.\Rightarrow \left\{ \begin{array} {} {{t}_{1}}=\frac{9}{5};{{t}_{2}}=\frac{1}{5} \\ {} {{t}_{1}}.{{t}_{2}}=m-1 \\ \end{array} \right.$
$\Rightarrow m-1=\frac{9}{25}\Leftrightarrow m=\frac{34}{25}$ . Chọn B.
| Bài tập 7: Cho hàm số $y={{x}^{4}}-2(2m+1){{x}^{2}}+4{{m}^{2}}\left( C \right)$. Các giá trị của tham số thực m để đồ thị $\left( C \right)$ cắt trục hoành tại 4 điểm phân biệt có hoành độ ${{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}$thỏa mãn $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}=6$là
A. $m\ge -\frac{1}{4}$ B. $m=-\frac{1}{4}$ C. $m=1$ D. $m=\frac{1}{4}$ |
Lời giải chi tiết
PT hoành độ giao điểm hai đồ thị là ${{x}^{4}}-2(2m+1){{x}^{2}}+4{{m}^{2}}=0\xrightarrow{t={{x}^{2}}}{{t}^{2}}-2(2m+1)t+4{{m}^{2}}=0\left( * \right)$
Đồ thị cắt trục hoành tại 4 điểm $\Leftrightarrow (*)$ có 2 nghiệm dương phân biệt $\left\{ \begin{array} {} {\Delta }’>0 \\ {} {{t}_{1}}+{{t}_{2}}>0 \\ {} {{t}_{1}}.{{t}_{2}}>0 \\ \end{array} \right.$
$\Leftrightarrow \left\{ \begin{array} {} {{(2m+1)}^{2}}-4{{m}^{2}}>0 \\ {} 2(2m+1)>0 \\ {} 4{{m}^{2}}>0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} m>-\frac{1}{4} \\ {} m\ne 0 \\ \end{array} \right.\Rightarrow \left\{ \begin{array} {} {{t}_{1}}=x_{1}^{2}=x_{2}^{2} \\ {} {{t}_{1}}=x_{3}^{2}=x_{4}^{2} \\ \end{array} \right.$
Khi đó $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}=2({{t}_{1}}+{{t}_{2}})=4\left( 2m+1 \right)=6\Leftrightarrow m=\frac{1}{4}$ thỏa mãn $\left\{ \begin{array} {} m>-\frac{1}{4} \\ {} m\ne 0 \\ \end{array} \right.$ . Chọn D.
| Bài tập 8: Cho hàm số $y={{x}^{4}}-(4m+2){{x}^{2}}+2{{m}^{2}}+1\left( C \right)$. Có bao nhiêu giá trị của m để $\left( C \right)$ chia trục hoành thành 4 đoạn phân biệt có độ dài bằng nhau.
A. 0 B. 1 C. 2 D. 3 |
Lời giải chi tiết
Phương trình hoành độ giao điểm của $\left( C \right)$ và Ox là ${{x}^{4}}-(4m+2){{x}^{2}}+2{{m}^{2}}+1=0\left( 1 \right)$
Đặt $t={{x}^{2}}:\left( 1 \right)\Rightarrow {{t}^{2}}-(4m+2)t+2{{m}^{2}}+1=0\left( 2 \right)$
Để $\left( C \right)$ cắt trục Ox tại 4 điểm phân biệt $\Leftrightarrow (2)$ có 2 nghiệm phân biệt ${{t}_{1}}>{{t}_{2}}>0$
$\Leftrightarrow \left\{ \begin{array} {} {\Delta }’={{\left( 2m+1 \right)}^{2}}-2{{m}^{2}}-1>0 \\ {} S=\left( 4m+2 \right)>0 \\ {} P=2{{m}^{2}}+1>0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} 2{{m}^{2}}+4m>0 \\ {} 2m+1>0 \\ \end{array} \right.\left( * \right)$ .
Theo định lý Viet ta có: $\left\{ \begin{array} {} {{t}_{1}}+{{t}_{2}}=4m+2 \\ {} {{t}_{1}}.{{t}_{2}}=2{{m}^{2}}+1 \\ \end{array} \right.$
Khi đó PT (1) có 4 điểm A, B, C, D theo thứ tự hoành độ tăng dần là: $-\sqrt{{{t}_{1}}};-\sqrt{{{t}_{2}}};\sqrt{{{t}_{2}}};\sqrt{{{t}_{1}}}$
Ta có: $AB=CD=\sqrt{{{t}_{1}}}-\sqrt{{{t}_{2}}};BC=2\sqrt{{{t}_{2}}}\Rightarrow AB=BC=CD\Leftrightarrow \sqrt{{{t}_{1}}}=3\sqrt{{{t}_{2}}}\Leftrightarrow {{t}_{1}}=9{{t}_{2}}$
Giải hệ: $\left\{ \begin{array} {} {{t}_{1}}+{{t}_{2}}=4m+2 \\ {} {{t}_{1}}=9{{t}_{2}} \\ {} {{t}_{1}}.{{t}_{2}}=2{{m}^{2}}+1 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} {{t}_{1}}=9.\frac{2m+1}{5},{{t}_{2}}=\frac{2m+1}{5} \\ {} {{t}_{1}}.{{t}_{2}}=2{{m}^{2}}+1 \\ \end{array} \right.\Rightarrow 9{{\left( 2m+1 \right)}^{2}}=25\left( 2{{m}^{2}}+1 \right)$
$\Leftrightarrow 7{{m}^{2}}-18m+8=0\Leftrightarrow \left[ \begin{array} {} m=2 \\ {} m=\frac{4}{7} \\ \end{array} \right.\left( t/m(*) \right)$ . Vậy $m=2,m=\frac{4}{7}$ là giá trị cần tìm. Chọn C.