Bài toán cực trị liên quan đến góc trong không gian oxyz
Phương pháp đại số
- Gọi véc tơ pháp tuyến hoặc véc tơ chỉ phương của mặt phẳng (hoặc đường thẳng) cần lập là $\left( a;b;c \right)$ trong đó ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}>0$.
- Thiết lập một phương trình quy ẩn (a theo b,c hoặc ngược lại) từ một dữ kiện về mặt phẳng chứa đường, song song hoặc vuông góc. Giả sử phương trình thu gọn ẩn là $a=f\left( b;c \right).$
- Thiết lập phương trình về góc, thay $a=f\left( b;c \right).$ vào ta được một phương trình hai ẩn b,c.
Chú ý:
- Góc giữa hai đường thẳng $\cos \left( {{d}_{1}};{{d}_{2}} \right)=\left| \cos \left( \overrightarrow{{{u}_{1}}};\overrightarrow{{{u}_{2}}} \right) \right|=\frac{\left| \overrightarrow{{{u}_{1}}}.\overrightarrow{{{u}_{2}}} \right|}{\left| \overrightarrow{{{u}_{1}}} \right|.\left| \overrightarrow{{{u}_{2}}} \right|}$
- Góc giữa hai mặt phẳng $\cos \left( {{\left( P \right)}_{1}};\left( {{P}_{2}} \right) \right)=\left| \cos \left( \overrightarrow{{{n}_{1}}};\overrightarrow{{{n}_{2}}} \right) \right|=\frac{\left| \overrightarrow{{{n}_{1}}}.\overrightarrow{{{n}_{2}}} \right|}{\left| \overrightarrow{{{n}_{1}}} \right|.\left| \overrightarrow{{{n}_{2}}} \right|}$
- Góc giữa đường thẳng và mặt phẳng $sin\left( d;\left( P \right) \right)=\left| \cos \left( \overrightarrow{{{n}_{P}}};\overrightarrow{{{u}_{d}}} \right) \right|=\frac{\left| \overrightarrow{{{n}_{P}}}.\overrightarrow{{{u}_{d}}} \right|}{\left| \overrightarrow{{{n}_{P}}} \right|.\left| \overrightarrow{{{u}_{d}}} \right|}$
- Ta biết rằng hàm $\sin \varphi $đồng biến khi $0<\varphi <90{}^\circ $, ngược lại hàm $\cos \varphi $ nghịch biến .
Vậy khi hàm xét max, min là hàm sin thì góc lớn ứng với hàm max,, góc nhỏ ứng với hàm nhỏ. Còn khi hàm xét max, min là hàm cosin thì ngược lại, đề bài yêu cầu tìm góc lớn thì hàm phải đạt min, góc nhỏ thì hàm đạt max.
Phương pháp hình học
Bài toán 1: Lập phương trình mặt phẳng $\left( Q \right)$ chứa $\Delta $ sao cho mặt phẳng $\left( Q \right)$ tạo với mặt phẳng $\left( P \right)$cho trước một góc nhỏ nhất (hoặc tạo với đường thẳng d cho trước một góc lớn nhất)
Phương pháp giải:
– TH1: ${{\left( \widehat{\left( P \right);\left( Q \right)} \right)}_{\min }}$
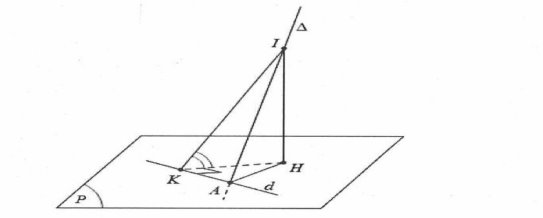
Gọi $A=\Delta \cap \left( P \right);d=\left( P \right)\cap \left( Q \right)$với $\left( Q \right)$là mặt phẳng $\left( IAK \right)$ trong hình vẽ.
Lấy $I\in \Delta \Rightarrow A;I$cố định, dựng $IH\bot d\Rightarrow \left( \widehat{\left( P \right);\left( Q \right)} \right)=\widehat{IKH}=\varphi .$
Do $IA\ge IK\Rightarrow \sin \varphi =\frac{IH}{IK}\ge \frac{IH}{IA}\Rightarrow {{\varphi }_{\min }}$khi $K\equiv A$tức là $\Delta \bot d\Leftrightarrow \Delta \bot \left( P \right)\Rightarrow \overrightarrow{{{n}_{Q}}}=\left[ \overrightarrow{{{u}_{\Delta }}};\overrightarrow{{{u}_{d}}} \right]$
Mặt khác $\left\{ \begin{array} {} IA\bot d \\ {} d\subset \left( P \right) \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} \Delta \bot d \\ {} d\subset \left( P \right) \\ \end{array} \right.\Rightarrow \overrightarrow{{{u}_{d}}}=\left[ \overrightarrow{{{u}_{\Delta }}};\overrightarrow{{{n}_{\left( P \right)}}} \right]$
Suy ra $\left( \widehat{\left( P \right);\left( Q \right)} \right)$nhỏ nhất $\Leftrightarrow \Delta \bot $giao tuyến d của $\left( P \right)$và $\left( Q \right)$$\Leftrightarrow \overrightarrow{{{n}_{\left( Q \right)}}}=\left[ \overrightarrow{{{u}_{\Delta }}};\left[ \overrightarrow{{{u}_{\Delta }}};\overrightarrow{{{n}_{\left( P \right)}}} \right] \right]$
-TH2: ${{\left( \widehat{\left( Q \right);d} \right)}_{\max }}\Leftrightarrow $$\overrightarrow{{{n}_{\left( Q \right)}}}=\left[ \overrightarrow{{{u}_{\Delta }}};\left[ \overrightarrow{{{u}_{\Delta }}};\overrightarrow{{{u}_{d}}} \right] \right]$
| Tổng kết: $\left\{ \begin{array} {} {{\left( \widehat{\left( P \right);\left( Q \right)} \right)}_{\min }}\Leftrightarrow \overrightarrow{{{n}_{\left( Q \right)}}}=\left[ \overrightarrow{{{u}_{\Delta }}};\left[ \overrightarrow{{{u}_{\Delta }}};\overrightarrow{{{n}_{\left( P \right)}}} \right] \right] \\ {} {{\left( \widehat{\left( Q \right);d} \right)}_{\max }}\Leftrightarrow \overrightarrow{{{n}_{\left( Q \right)}}}=\left[ \overrightarrow{{{u}_{\Delta }}};\left[ \overrightarrow{{{u}_{\Delta }}};\overrightarrow{{{u}_{d}}} \right] \right] \\ \end{array} \right.$ |
| Bài tập 1: Cho $d:\frac{x+2}{1}=\frac{y+2}{2}=\frac{z}{-1};{d}’:\frac{x+2}{2}=\frac{y-1}{-1}=\frac{z}{2};\left( Q \right):x+2y+2z-3=0$
Lập chứa d sao cho a) Góc giữa $\left( P \right)$và $\left( Q \right)$ nhỏ nhất. b) Góc giữa $\left( P \right)$và ${d}’$lớn nhất. |
Lời giải chi tiết:
a) Ta có: $\overrightarrow{{{u}_{d}}}=\left( 1;2;-1 \right)$và $\overrightarrow{{{n}_{\left( Q \right)}}}=\left( 1;2;2 \right)$. Đường thẳng d đi qua $M\left( 1;-2;0 \right).$
${{\left( \widehat{\left( P \right);\left( Q \right)} \right)}_{\min }}\Leftrightarrow \overrightarrow{{{n}_{\left( P \right)}}}=\left[ \overrightarrow{{{u}_{d}}};\left[ \overrightarrow{{{u}_{d}}};\overrightarrow{{{n}_{\left( Q \right)}}} \right] \right]=\left( -3;-6;-15 \right)=-3\left( 1;2;5 \right)$
Mặt phẳng $\left( P \right)$đi qua điểm M và có véc tơ pháp tuyến $\overrightarrow{n}=\left( 1;2;5 \right)$có phương trình là:
$\left( P \right):x+2y+5z+3=0$.
b) Ta có: $\overrightarrow{{{u}_{{{d}’}}}}=\left( 2;-1;2 \right).$
Để ${{\left( \widehat{\left( P \right);{d}’} \right)}_{\max }}\Leftrightarrow \overrightarrow{{{n}_{\left( P \right)}}}=\left[ \overrightarrow{{{u}_{d}}};\left[ \overrightarrow{{{u}_{d}}};\overrightarrow{{{u}_{{{d}’}}}} \right] \right]=\left( -14;2;-10 \right)=-2\left( 7;-1;5 \right)$
Mặt phẳng $\left( P \right)$đi qua điểm M và có véc tơ pháp tuyến $\overrightarrow{n}=\left( 7;-1;5 \right)$
Phương trình mặt phẳng $\left( P \right):7x-y+5z-9=0$.
| Bài tập 2: Trong không gian với hệ tọa độ $Oxyz$cho mặt phẳng $(P):2x-y-2z-2=0$ và đường thẳng $\Delta :\frac{x}{-1}=\frac{y+1}{2}=\frac{z-2}{1}$ . Gọi $\left( Q \right)$ là mặt phẳng chứa $\Delta $và tạo với $\left( P \right)$ một góc nhỏ nhất. Khoảng cách từ gốc tọa độ O đến mặt phẳng $\left( Q \right)$bằng
A.$\sqrt{3}.$ B.$\frac{\sqrt{2}}{3}.$ C.$\sqrt{5}.$ D. 1. |
Lời giải chi tiết:
Ta có: $\overrightarrow{{{n}_{\left( P \right)}}}=\left( 2;-1;-2 \right);\overrightarrow{{{u}_{\Delta }}}\left( -1;2;1 \right)$ và đường thẳng $\Delta $ đi qua $A\left( 0;-1;2 \right).$
$\left( \widehat{\left( P \right);\left( Q \right)} \right)$ nhỏ nhất $\Leftrightarrow \overrightarrow{{{n}_{\left( Q \right)}}}=\left[ \overrightarrow{{{u}_{\Delta }}};\left[ \overrightarrow{{{u}_{\Delta }}};\overrightarrow{{{n}_{\left( P \right)}}} \right] \right]$
Ta có: $\overrightarrow{{{u}_{d}}}=\left[ \overrightarrow{{{u}_{\Delta }}};\overrightarrow{{{n}_{\left( P \right)}}} \right]=-3\left( 1;0;1 \right)$suy ra $\overrightarrow{{{n}_{\left( Q \right)}}}=\left[ \overrightarrow{{{u}_{d}}};\overrightarrow{{{u}_{\Delta }}} \right]=-2\left( 1;1;-1 \right)$
Khi đó $\left( Q \right)$đi qua $A\left( 0;-1;2 \right)$và $\overrightarrow{n}=\left( 1;1;-1 \right)$ $\left( Q \right):x+y-z+3=0\Rightarrow d\left( O;\left( Q \right) \right)=\sqrt{3}.$ Chọn A.
Bài tập 3: Trong không gian với hệ tọa độ $Oxyz$cho mặt phẳng $(P):2x-2y-z+1=0$ và đường thẳng $\Delta :\frac{x-1}{1}=\frac{y}{-1}=\frac{z}{-2}$ . Gọi $\left( Q \right)$ là mặt phẳng chứa $\Delta $và tạo với $\left( P \right)$ một góc nhỏ nhất. Tính cosin góc $\varphi $giữa 2 mặt phẳng $\left( P \right)$và $\left( Q \right)$khi đó:
| A. $\cos \varphi =\frac{1}{3}.$ | B. $\cos \varphi =\frac{\sqrt{3}}{3}.$ | C. $\cos \varphi =\frac{\sqrt{2}}{2}.$ | D. $\cos \varphi =\frac{1}{2}.$ |
Lời giải chi tiết:
Ta có: $\overrightarrow{{{u}_{\Delta }}}=\left( 1;-1;-2 \right);\overrightarrow{{{n}_{\left( P \right)}}}\left( 2;-2;-1 \right)$ và đường thẳng $\Delta $ đi qua $M\left( 1;0;0 \right).$
Để ${{\left( \widehat{\left( P \right);\left( Q \right)} \right)}_{\min }}\Leftrightarrow \overrightarrow{{{n}_{\left( Q \right)}}}=\left[ \overrightarrow{{{u}_{\Delta }}};\left[ \overrightarrow{{{u}_{\Delta }}};\overrightarrow{{{n}_{\left( P \right)}}} \right] \right]=\left( -6;6;-6 \right)=-6\left( 1;-1;1 \right).$
Suy ra $cos\varphi =\frac{\left| 2.1+2-1 \right|}{\sqrt{4+4+1}.\sqrt{3}}=\frac{\sqrt{3}}{3}$. Chọn B.
Bài tập 4: Trong không gian với hệ tọa độ $Oxyz$cho mặt phẳng $(P):x+2y-z+3=0$ và đường thẳng $d:\frac{x+1}{2}=\frac{y+1}{1}=\frac{z-3}{1}$ . Mặt phẳng $\left( Q \right)$ chứa đường thẳng d và tạo với mặt phẳng $\left( P \right)$ một góc nhỏ nhất. Khoảng cách từ O đến $\left( Q \right)$bằng:
| A. $4\sqrt{2}.$ | B. $\sqrt{2}.$ | C. $2.$ | D. $2\sqrt{2}.$ |
Lời giải chi tiết:
Ta có: $\overrightarrow{{{u}_{d}}}=\left( 2;1;1 \right);\overrightarrow{{{n}_{\left( P \right)}}}\left( 1;2;-1 \right)$ và đường thẳng $\Delta $ đi qua $M\left( -1;-1;3 \right).$
${{\left( \widehat{\left( P \right);\left( Q \right)} \right)}_{\min }}\Leftrightarrow \overrightarrow{{{n}_{\left( Q \right)}}}=\left[ \overrightarrow{{{u}_{d}}};\left[ \overrightarrow{{{u}_{d}}};\overrightarrow{{{n}_{\left( P \right)}}} \right] \right]=\left( 0;-9;9 \right)=-9\left( 0;1;-1 \right).$
Phương trình mặt phẳng $\left( P \right)$cần tìm đi qua điểm $M\left( -1;-1;3 \right).$và có véc tơ pháp tuyến ${{\overrightarrow{n}}_{\left( Q \right)}}=\left( 0;1;-1 \right)$
Suy ra $\left( P \right):y-z+4=0\Rightarrow d\left( O;Q \right)=\frac{4}{\sqrt{2}}=2\sqrt{2}.$ Chọn D.
Bài tập 5: Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $d:\frac{x-1}{-1}=\frac{z+2}{1}=\frac{z}{2}$ . Gọi $\left( P \right)$ là mặt phẳng chứa d và tạo với trục Oy một góc lớn nhất. Mặt phẳng $\left( P \right)$đi qua điểm nào trong các điểm sau:
| A. $A\left( 6;-3;0 \right).$ | B. $B\left( 2;-3;0 \right).$ | C. $C\left( 2;1;-1 \right).$ | D. $D\left( 2;1;1 \right).$ |
Lời giải chi tiết:
Ta có: $\overrightarrow{{{u}_{d}}}=\left( -1;1;2 \right);\overrightarrow{{{u}_{Oy}}}\left( 0;1;0 \right)$ và đường thẳng d đi qua $M\left( 1;-2;0 \right).$
Để ${{\left( \widehat{\left( P \right);Oy} \right)}_{\max }}\Leftrightarrow \overrightarrow{{{n}_{\left( P \right)}}}=\left[ \overrightarrow{{{u}_{d}}};\left[ \overrightarrow{{{u}_{d}}};\overrightarrow{{{u}_{Oy}}} \right] \right]=\left( -1;-5;2 \right)=-1\left( 1;5;-2 \right).$
Mặt phẳng $\left( P \right)$đi qua điểm M và có véc tơ pháp tuyến $\overrightarrow{n}=\left( 1;5;-2 \right)$
Phương trình mặt phẳng $\left( P \right):x+5y-2z+9=0$.
Do đó $\left( P \right)$đi qua điểm $A\left( 6;-3;0 \right).$ Chọn A.
Bài tập 6: Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A\left( 1;2;-1 \right);B\left( -1;1;2 \right)$. Gọi $\left( Q \right)$ là phương trình mặt phẳng đi qua 2 điểm A, B sao cho $\left( Q \right)$tạo với mặt phẳng$\left( Oxy \right)$ một góc nhỏ nhất. Khoảng cách từ gốc O đến mặt phẳng $\left( Q \right)$bằng:
| A. $d=\frac{7}{\sqrt{35}}.$ | B. $d=\frac{\sqrt{70}}{10}.$ | C. $d=\frac{\sqrt{70}}{70}.$ | D. $d=\frac{\sqrt{70}}{35}.$ |
Lời giải chi tiết:
Ta có: $\overrightarrow{AB}=\left( -2;-1;3 \right);\overrightarrow{{{n}_{\left( Oxy \right)}}}\left( 0;0;1 \right).$
Để ${{\left( \widehat{\left( P \right);Oxy} \right)}_{\min }}\Leftrightarrow \overrightarrow{{{n}_{Q}}}=\left[ \overrightarrow{AB};\left[ \overrightarrow{AB};\overrightarrow{{{n}_{\left( Oxy \right)}}} \right] \right]=\left( -6;-3;-5 \right)=-\left( 6;3;5 \right).$
Phương trình mặt phẳng $\left( Q \right)$là: $6x+3y+5z-7=0\Rightarrow d\left( O;\left( Q \right) \right)=\frac{7}{\sqrt{{{6}^{2}}+{{3}^{2}}+{{5}^{2}}}}=\frac{\sqrt{70}}{10}.$Chọn B.
Bài toán 2: Viết phương trình đường thẳng ${d}’$ qua A nằm trong$\left( P \right)$sao cho góc giữa 2 đường thẳng d và ${d}’$nhỏ nhất (hoặc tạo với mặt phẳng $\left( Q \right)$ cho trước một góc lớn nhất)
Phương pháp giải:
– TH1: ${{\left( \widehat{d;{d}’} \right)}_{\min }}$
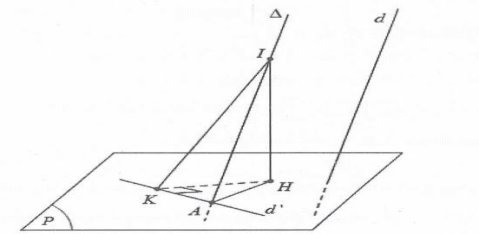
Qua A dựng đường thẳng $\Delta \parallel d$ , trên $\Delta $lấy điểm I, hạ $IH\bot \left( P \right)\Rightarrow A,I,H$ cố định, điểm K thay đổi
$\left( \widehat{d;{d}’} \right)=\left( \widehat{\Delta ;{d}’} \right)=\widehat{IAK}=\alpha $
Mà $sin\alpha =\frac{IK}{IA}\ge \frac{IH}{IA}$ (Do $IK\ge IH$) suy ra ${{\alpha }_{\operatorname{mi}}}_{n}\Leftrightarrow H\equiv K$hay ${d}’$qua A và H.
Khi đó ${d}’$là hình chiếu vuông góc của $\Delta $ trên $\left( P \right)$.
Ta có: ${{\left( \widehat{d;{d}’} \right)}_{\min }}\Leftrightarrow \overrightarrow{{{u}_{{{d}’}}}}=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{{{n}_{AIH}}} \right]=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{{{u}_{d}}} \right] \right].$
– TH2: ${{\left( \widehat{d;\left( Q \right)} \right)}_{\max }}\Leftrightarrow \overrightarrow{{{u}_{{{d}’}}}}=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{{{n}_{Q}}} \right] \right].$
| Tổng kết: $\left\{ \begin{array} {} {{\left( \widehat{d;{d}’} \right)}_{\min }}\Leftrightarrow \overrightarrow{{{u}_{{{d}’}}}}=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{{{u}_{d}}} \right] \right] \\ {} {{\left( \widehat{d;\left( Q \right)} \right)}_{\max }}\Leftrightarrow \overrightarrow{{{u}_{{{d}’}}}}=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{{{n}_{\left( Q \right)}}} \right] \right]. \\ \end{array} \right.$ |
| Bài tập 1: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A\left( 1;-1;2 \right)$ và mặt phẳng $\left( P \right):2x-y-z+3=0$. Lập phương trình đường thẳng d đi qua A; song song với $\left( P \right)$đồng thời tạo với đường $\Delta :\frac{x+1}{1}=\frac{y-1}{-2}=\frac{z}{2}$ một góc nhỏ nhất. |
Lời giải chi tiết:
Gọi $\left( \alpha \right)$là mặt phẳng chứa A và song song với $\left( P \right)\Rightarrow \overrightarrow{{{n}_{\left( \alpha \right)}}}=\left( 2;-1;-1 \right).$
Khi đó d nằm trong $\left( \alpha \right)$ sao cho góc giữa d và $\Delta $ nhỏ nhất.
Ta có: ${{\left( \widehat{d;\Delta } \right)}_{\min }}\Leftrightarrow \overrightarrow{{{u}_{d}}}=\left[ \overrightarrow{{{n}_{\left( \alpha \right)}}};\left[ \overrightarrow{{{u}_{\Delta }}};\overrightarrow{{{n}_{\left( \alpha \right)}}} \right] \right]=-2\left( 1;-5;7 \right)$
Phương trình đường thẳng d là: $d:\frac{x-1}{1}=\frac{y+1}{-5}=\frac{z-2}{7}.$
| Bài tập 2: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A\left( 1;-1;2 \right)$ và hai đường $d:\frac{x-1}{2}=\frac{y-2}{1}=\frac{z+2}{-1};{d}’:\frac{x-3}{-1}=\frac{y-2}{2}=\frac{z+3}{2}$. Lập phương trình đường thẳng $\Delta $ đi qua A đồng thời cắt đường d sao cho góc giữa $\Delta $và ${d}’$nhỏ nhất? |
Lời giải chi tiết:
Gọi $\left( P \right)$ là mặt phẳng chứa A và d.
Đường thẳng d đi qua điểm $A\left( 1;2;-2 \right)$và có VTCP là $\overrightarrow{{{u}_{d}}}=\left( 2;1;-1 \right).$
Khi đó $\overrightarrow{{{n}_{\left( P \right)}}}=\left[ \overrightarrow{AM};\overrightarrow{{{u}_{d}}} \right]=-\left( 1;0;2 \right)$. Đường thẳng $\Delta \subset \left( P \right)$.
Ta có: ${{\left( \widehat{\Delta ;{d}’} \right)}_{\min }}\Leftrightarrow \overrightarrow{{{u}_{\Delta }}}=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{{{u}_{{{d}’}}}} \right] \right]=\left( 8;-10;-4 \right)=2\left( 4;-5;-2 \right).$
Phương trình đường thẳng là: $d:\frac{x+1}{4}=\frac{y}{-5}=\frac{z+1}{-2}.$
| Bài tập 3: Trong không gian với hệ tọa độ $Oxyz$, lập phương trình đường thẳng d đi qua $A\left( 1;0;-2 \right)$ và cắt $\Delta :\frac{x-1}{3}=\frac{y+1}{2}=\frac{z-2}{-2}$ sao cho góc giữa d và mặt phẳng $\left( P \right):2x-y+2z-1=0$ lớn nhất?. |
Lời giải chi tiết:
Đường thẳng d nằm trong mặt phẳng $\left( Q \right)$ chứa A và $\Delta $ .
Đường thẳng $\Delta $ đi qua điểm $M\left( 1;-1;2 \right)$và có VTCP là $\overrightarrow{{{u}_{\Delta }}}=\left( 3;2;-2 \right),\overrightarrow{AM}\left( 0;-1;4 \right)$
Ta có: $\overrightarrow{{{n}_{\left( Q \right)}}}=\left[ \overrightarrow{AM};\overrightarrow{{{u}_{\Delta }}} \right]=-\left( -6;12;3 \right)\Rightarrow \overrightarrow{{{n}_{\left( Q \right)}}}=\left( -2;4;1 \right)$.
Để ${{\left( \widehat{d;\left( P \right)} \right)}_{\max }}\Leftrightarrow \overrightarrow{{{u}_{d}}}=\left[ \overrightarrow{{{n}_{\left( Q \right)}}};\left[ \overrightarrow{{{n}_{\left( Q \right)}}};\overrightarrow{{{n}_{\left( P \right)}}} \right] \right]=\left( -30;-3;-48 \right)=-3\left( 10;1;16 \right).$
Khi đó phương trình đường thẳng $d:\frac{x-1}{10}=\frac{y}{1}=\frac{z+2}{16}.$
Bài tập 4: Trong không gian với hệ tọa độ $Oxyz$, đường thẳng $\Delta $ đi qua $A\left( 1;0;1 \right)$, nằm trong mặt phẳng $\left( P \right):2x+y-z-1=0$ và tạo với đường thẳng $d:\frac{x}{2}=\frac{y-1}{-1}=\frac{z+1}{2}$ một góc nhỏ nhất. Biết $\overrightarrow{u}=\left( 5;b;c \right)$ là một véc tơ chỉ phương của đường thẳng $\Delta $ . Tìm b + c.
|
Lời giải chi tiết:
Ta có: $\overrightarrow{{{n}_{\left( P \right)}}}=\left( 2;1;-1 \right);\overrightarrow{{{u}_{d}}}=\left( 2;-1;2 \right).$
Để ${{\left( \widehat{d;\Delta } \right)}_{\min }}\Leftrightarrow \overrightarrow{{{u}_{\Delta }}}=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{{{u}_{d}}} \right] \right]=\left( -10;7;-13 \right)=-2\left( \frac{5}{2};-\frac{7}{2};\frac{13}{2} \right).$
Do đó: $b=-\frac{7}{2};c=\frac{13}{2}\Rightarrow b+c=3.$Chọn D.
| Bài tập 5: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A\left( 3;-1;1 \right)$, đường thẳng $\Delta :\frac{x}{1}=\frac{y-2}{2}=\frac{z}{2}$, mặt phẳng $\left( P \right):x-y+z-5=0$. Gọi d là đường thẳng đi điểm qua A nằm trong $\left( P \right)$ và tạo với $\Delta $ một góc bé nhất là $\alpha $. Tính $sin\alpha $.
A. $\frac{\sqrt{78}}{9}.$ B. $\frac{\sqrt{3}}{9}.$ C. $\frac{\sqrt{6}}{9}.$ D. $\frac{\sqrt{75}}{9}.$ |
Lời giải chi tiết:
Ta có: $\overrightarrow{{{n}_{\left( P \right)}}}=\left( 1;-1;1 \right);\overrightarrow{{{u}_{\Delta }}}=\left( 1;2;2 \right).$
Để ${{\left( \widehat{d;\Delta } \right)}_{\min }}\Leftrightarrow \overrightarrow{{{u}_{d}}}=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{{{u}_{\Delta }}} \right] \right]=\left( -2;-7;-5 \right)=-\left( 2;7;5 \right).$
Phương trình đường thẳng d là: $d:\frac{x-3}{2}=\frac{y+1}{7}=\frac{z-1}{5}.$
Khi đó $cos\alpha =\left| \cos \left( \overrightarrow{{{u}_{\Delta }}};\overrightarrow{{{u}_{d}}} \right) \right|=\frac{\left| 2+14+10 \right|}{3.\sqrt{{{2}^{2}}+{{7}^{2}}+{{5}^{2}}}}=\frac{\sqrt{78}}{9}.\Rightarrow sin\alpha =\sqrt{1-{{\cos }^{2}}\alpha }=\frac{\sqrt{3}}{9}.$Chọn B.
| Bài tập 6: Trong không gian với hệ tọa độ $Oxyz$, gọi d là đường thẳng song song với $\left( P \right):x-2y+2z-5=0$ , đồng thời tạo với mặt phẳng $\left( Oyz \right)$một góc lớn nhất là $\varphi $. Tính $P=\sin \varphi $.
A.$P=1.$ B. $P=\frac{2\sqrt{2}}{3}.$ C. $P=\frac{1}{3}.$ D. $P=\frac{1}{2}.$ |
Lời giải chi tiết:
Gọi $Q\equiv \left( Oyz \right)\Rightarrow \overrightarrow{{{n}_{\left( Q \right)}}}=\left( 1;0;0 \right);\overrightarrow{{{n}_{\left( P \right)}}}=\left( 1;-2;2 \right).$
Ta có $\varphi ={{\left( \widehat{d;\left( Q \right)} \right)}_{\max }}\Leftrightarrow \overrightarrow{{{u}_{d}}}=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{{{n}_{\left( Q \right)}}} \right] \right]=\left( -8;-2;2 \right)=-2\left( 4;1;-1 \right).$
Suy ra $\sin \varphi =\left| \cos \left( \overrightarrow{{{u}_{d}}};\overrightarrow{{{n}_{\left( Q \right)}}} \right) \right|=\frac{4}{\sqrt{18}}=\frac{2\sqrt{2}}{3}$. Chọn B.
| Bài tập 7: Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $\left( P \right):2x-y+z-1=0$, điểm $A\left( 2;3;0 \right)$ thuộc mặt phẳng $\left( P \right)$và đường thẳng $d:\frac{x+1}{1}=\frac{y}{-1}=\frac{z-1}{1}$. Đường thẳng ${d}’$qua A nằm trong $\left( P \right)$sao cho góc giữa 2 đường thẳng d và ${d}’$ nhỏ nhất đi qua điểm nào trong các điểm sau:
A. $\left( 0;0;1 \right)$. B. $\left( 2;4;1 \right).$ C. $\left( 1;1;0 \right)$. D. $\left( 1;2;1 \right).$ |
Lời giải chi tiết:
Ta có: $\overrightarrow{{{n}_{\left( P \right)}}}=\left( 2;-1;1 \right);\overrightarrow{{{u}_{d}}}=\left( 1;-1;1 \right).$
Do đó ${{\left( \widehat{d;{d}’} \right)}_{\min }}\Leftrightarrow \overrightarrow{{{u}_{{{d}’}}}}=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{{{u}_{d}}} \right] \right]=\left( 2;2;-2 \right)=2\left( 1;1;-1 \right)\Rightarrow {d}’:\frac{x-2}{1}=\frac{y-3}{1}=\frac{z}{-1}.$
Vậy ${d}’$ đi qua hai điểm $\left( 1;2;1 \right).$ Chọn D.
| Ví dụ 8: Cho mặt phẳng $\left( P \right):x-y+z-2=0$ điểm $A\left( 2;1;1 \right)$ thuộc mặt phẳng $\left( P \right)$và đường thẳng $d:\frac{x-1}{-1}=\frac{y}{2}=\frac{z+1}{2}$. Đường thẳng ${d}’$qua A nằm trong $\left( P \right)$sao cho góc giữa 2 đường thẳng d và ${d}’$ nhỏ nhất cắt mặt phẳng $\left( Oyz \right)$tại điểm E. Tính $P=OE$.
A. $P=14.$ B. $P=2\sqrt{6}.$ C. $P=10.$ D. $P=\sqrt{14}.$ |
Lời giải:
Ta có: $\overrightarrow{{{n}_{\left( P \right)}}}=\left( 1;-1;1 \right);\overrightarrow{{{u}_{d}}}=\left( -1;2;2 \right)\Rightarrow \left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{{{u}_{d}}} \right]=\left( 4;3;-1 \right)$
Ta có: ${{\left( \widehat{d;{d}’} \right)}_{\min }}\Leftrightarrow \overrightarrow{{{u}_{{{d}’}}}}=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{{{u}_{d}}} \right] \right]=-\left( 2;-5;-7 \right)\Rightarrow {d}’:\frac{x-2}{2}=\frac{y-1}{-5}=\frac{z-1}{-7}.$
Vậy ${d}’$ cắt mặt phẳng $x=0$ tại điểm $E\left( 0;6;8 \right)\Rightarrow OE=10.$ Chọn C…
