CÁCH NHẬN DẠNG ĐỒ THỊ HÀM SỐ BẬC 3: $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$ $\left( a\ne 0 \right)$
1. Giới hạn, đạo hàm và cực trị
Giới hạn:
– Với $a>0$ thì $\underset{x\to +\infty }{\mathop{\lim }}\,y=+\infty $ và $\underset{x\to -\infty }{\mathop{\lim }}\,y=-\infty $.
– Với $a<0$ thì $\underset{x\to +\infty }{\mathop{\lim }}\,y=-\infty $ và $\underset{x\to -\infty }{\mathop{\lim }}\,y=+\infty $.
Đạo hàm và cực trị: ${y}’=3a{{x}^{2}}+2bx+c$. Khi đó:
– Hàm số có hai điểm cực trị khi ${y}’=0$ có hai nghiệm phân biệt $\Leftrightarrow {{{\Delta }’}_{{{y}’}}}>0$.
Gọi $A\left( {{x}_{1}};{{y}_{1}} \right)$ và $B\left( {{x}_{2}};{{y}_{2}} \right)$ là hai tọa độ điểm cực trị thì theo định lý Viet ta có: $\left\{ \begin{array} {} {{x}_{1}}+{{x}_{2}}=\frac{-2b}{3a} \\ {} {{x}_{1}}{{x}_{2}}=\frac{c}{3a} \\ \end{array} \right.$
– Hàm số không có cực trị khi ${y}’=0$ vô nghiệm hoặc có nghiệm kép $\Leftrightarrow {{{\Delta }’}_{{{y}’}}}\le 0$
Chú ý: Đối với hàm số bậc ba ta luôn có ${{y}_{C\tilde{N}}}>{{y}_{CT}}$ và:
– Nếu $a>0$ thì ${{x}_{CÐ}}<{{x}_{CT}}$.
– Nếu $a{{x}_{CT}}$.
2. Bảng biến thiên
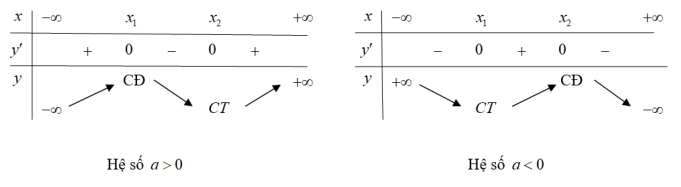
TH1: Hàm số có hai điểm cực trị  .
.
TH2: Hàm số không có điểm cực trị

3. Đồ thị hàm số
4. Phương pháp giải toán
Để nhận diện đồ thị hàm số bậc ba: $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$ $\left( a\ne 0 \right)$ ta làm như sau:
Ta có ${y}’=3a{{x}^{2}}+2bx+c$
Dựa vào $\underset{x\to +\infty }{\mathop{\lim }}\,y$ để xác định hệ số $a$:
– Nếu $a>0$ thì nhánh cuối của đồ thị đi lên $x;y$ tiến về vô cùng.
– Nếu $a<0$ thì nhánh cuối của đồ thị đi xuống $x\to +\infty $ và $y\to -\infty $.
Dựa vào giao điểm với trục tung $\left( 0;d \right)$ suy ra tính chất của hệ số $d$
Dựa vào số điểm cực trị của đồ thị hàm số suy ra số nghiệm của phương trình ${y}’=0$
Dựa vào vị trí của các điểm cực trị, tọa độ các điểm cực trị và các điểm mà đề bài đã cho thuộc đồ thị hàm số.
Trong trường hợp đồ thị hàm số có 2 điểm cực trị ${{x}_{1}};{{x}_{2}}$ ta có: $\left\{ \begin{array} {} {{x}_{1}}+{{x}_{2}}=\frac{-2b}{3a} \\ {} {{x}_{1}}{{x}_{2}}=\frac{c}{3a} \\ \end{array} \right.$ (định lý Viet)
Khi đó dựa vào ${{x}_{1}}+{{x}_{2}}=\frac{-2b}{3a}$ suy ra tính chất của b; dựa vào ${{x}_{1}}{{x}_{2}}=\frac{c}{3a}$ suy ra tính chất của c.
