Khảo sát chiều biến thiên của hàm số $y=f\left( x \right)$ dựa vào bảng xét dấu ${y}’$.
Phương pháp giải bài tìm khoảng đồng biến ngịch biến của hàm số
■ Bước 1. Tìm tập xác định D của hàm số. Tính đạo hàm ${y}’={f}’\left( x \right)$.
■ Bước 2. Tìm các điểm tại đó ${f}’\left( x \right)=0$ hoặc${f}’\left( x \right)$ không xác định.
■ Bước 3. Sắp xếp các điểm theo thứ tự tăng dần và lập bảng xét dấu của ${y}’$.
Dựa vào quy tắc xét dấu đã nêu để xét dấu cho ${y}’$.
■ Bước 4. Kết luận về các khoảng đồng biến và nghịch biến dựa vào bảng xét dấu của ${y}’$.
Bài tập tìm khoảng đồng biến nghịch biến có đáp án
| Bài tập 1: Tìm các khoảng đồng biến và nghịch biến của các hàm số sau
a) $y={{x}^{3}}-3{{x}^{2}}+2$ b) $y={{x}^{4}}-2{{x}^{2}}$ |
Lời giải chi tiết
a) TXĐ: $D=\mathbb{R}$
Ta có: ${y}’=3{{x}^{2}}-6x\Leftrightarrow \left\{ \begin{array} {} x=0 \\ {} x=2 \\ \end{array} \right.$
Bảng biến thiên (xét dấu ${y}’$):
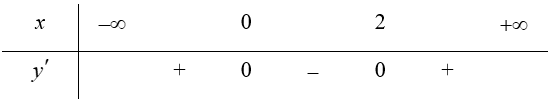
Vậy hàm số đồng biến trên các khoảng $\left( -\infty ;0 \right)$ và $\left( 2;+\infty \right)$, nghịch biến trên khoảng $\left( 0;2 \right)$.
b) TXĐ: $D=\mathbb{R}$
Ta có: ${y}’=4{{x}^{3}}-4x\Leftrightarrow \left\{ \begin{array} {} x=0 \\ {} x=\pm 1 \\ \end{array} \right.$
Bảng biến thiên (xét dấu ${y}’$):
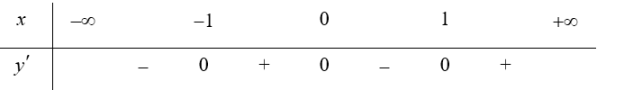
Vậy hàm số đồng biến trên các khoảng $\left( -1;0 \right)$ và $\left( 1;+\infty \right)$, nghịch biến trên khoảng $\left( -\infty ;-1 \right)$ và $\left( 0;1 \right)$
| Bài tập 2: Tìm các khoảng đồng biến và nghịch biến của các hàm số sau
a) $y=-{{x}^{3}}+3x-2$ b) $y={{x}^{4}}-4{{x}^{3}}+2$ |
Lời giải chi tiết
a) TXĐ: $D=\mathbb{R}$
Ta có: ${y}’=-3{{x}^{2}}+3=0\Leftrightarrow \left\{ \begin{array} {} x=-1 \\ {} x=1 \\ \end{array} \right.$
Bảng biến thiên (xét dấu ${y}’$):
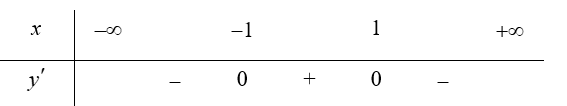
Vậy hàm số đồng biến trên các khoảng $\left( -1;1 \right)$ và nghịch biến trên khoảng $\left( -\infty ;-1 \right)$ và $\left( 1;+\infty \right)$.
b) TXĐ: $D=\mathbb{R}$
Ta có: ${y}’=4{{x}^{3}}-12{{x}^{2}}=4{{x}^{2}}\left( x-3 \right)$
Bảng biến thiên (xét dấu ${y}’$):
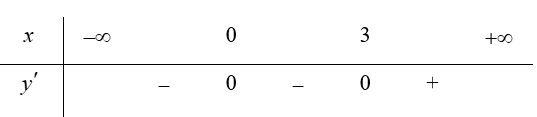
Vậy hàm số đồng biến trên các khoảng $\left( 3;+\infty \right)$, nghịch biến trên khoảng $\left( -\infty ;3 \right)$.
| Bài tập 3: Tìm các khoảng đồng biến và nghịch biến của các hàm số sau
a) $y=\frac{x+3}{x-1}$. b) $y=\frac{3x+1}{x+1}$. |
Lời giải chi tiết
a) TXĐ: $D=\mathbb{R}\backslash \left\{ 1 \right\}$
Ta có: ${y}’=\frac{-4}{{{\left( x-1 \right)}^{2}}}<0\left( \forall x\in D \right)$
Bảng biến thiên (xét dấu ${y}’$):

Vậy hàm số nghịch biến trên khoảng $\left( -\infty ;1 \right)$ và $\left( 1;+\infty \right)$.
b) TXĐ: $D=\mathbb{R}\backslash \left\{ -1 \right\}$
Ta có: ${y}’=\frac{2}{{{\left( x+1 \right)}^{2}}}>0\text{ }\left( \forall x\in D \right)$
Bảng biến thiên (xét dấu ${y}’$):
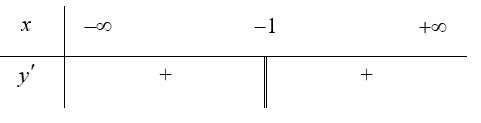
Vậy hàm số đồng biến trên các khoảng $\left( -\infty ;-1 \right)$ và $\left( -1;+\infty \right)$.
| Bài tập 4: Tìm các khoảng đồng biến và nghịch biến của các hàm số sau
a) $y=x+\frac{4}{x}$. b) $y=\frac{{{x}^{2}}-x+9}{x-1}$. |
Lời giải chi tiết
a) TXĐ: $D=\mathbb{R}\backslash \left\{ 0 \right\}$. Ta có: ${y}’=1-\frac{4}{{{x}^{2}}}=0\Leftrightarrow \left\{ \begin{array} {} x=2 \\ {} x=-2 \\ \end{array} \right.$
Bảng biến thiên (xét dấu ${y}’$):
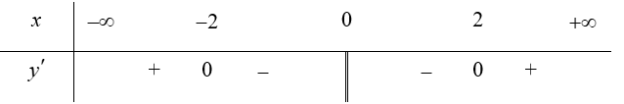
Vậy hàm số đồng biến trên các khoảng $\left( -\infty ;-2 \right)$ và $\left( 2;+\infty \right)$, hàm số nghịch biến trên khoảng $\left( -2;0 \right)$ và $\left( 0;2 \right)$.
b) TXĐ: $D=\mathbb{R}\backslash \left\{ 1 \right\}$
Ta có: ${y}’=\frac{\left( 2x-1 \right)\left( x-1 \right)-\left( {{x}^{2}}-x+9 \right)}{{{\left( x-1 \right)}^{2}}}=\frac{{{x}^{2}}-2x-8}{{{\left( x-1 \right)}^{2}}}=0\text{ }\Leftrightarrow \left\{ \begin{array} {} x=-2 \\ {} x=4 \\ \end{array} \right.$.
Bảng biến thiên (xét dấu ${y}’$):

Vậy hàm số đồng biến trên các khoảng $\left( -\infty ;-2 \right)$ và $\left( 4;+\infty \right)$, hàm số nghịch biến trên các khoảng $\left( -2;1 \right)$ và $\left( 1;4 \right)$.
| Bài tập 5: Tìm các khoảng đồng biến và nghịch biến của các hàm số sau
a) $y=\sqrt{16-{{x}^{2}}}$ b) $y=\sqrt{6x-{{x}^{2}}}$ |
Lời giải chi tiết
a) TXĐ: $D=\left[ -4;4 \right]$. Ta có: ${y}’=\frac{-2x}{2\sqrt{16-{{x}^{2}}}}=0\Leftrightarrow x=0$
Bảng biến thiên (xét dấu ${y}’$):
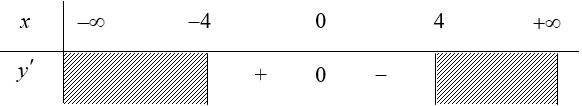
Vậy hàm số đồng biến trên khoảng $\left( -4;0 \right)$ và hàm số nghịch biến trên khoảng $\left( 0;4 \right)$.
b) TXĐ: $D=\left[ 0;6 \right]$
Ta có: ${y}’=\frac{6-2x}{2\sqrt{6x-{{x}^{2}}}}=0\text{ }\Leftrightarrow x=3$.
Bảng biến thiên (xét dấu ${y}’$):
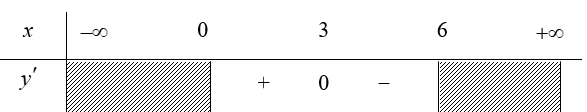
Vậy hàm số đồng biến trên khoảng $\left( 0;3 \right)$, hàm số nghịch biến trên khoảng $\left( 3;6 \right)$.
| Bài tập 6: Tìm các khoảng đồng biến và nghịch biến của các hàm số sau
a) $y=\sqrt{{{x}^{2}}-4x}$ b) $y=\sqrt{{{x}^{2}}-8x+12}$ |
Lời giải chi tiết
a) TXĐ: $D=\left( -\infty ;0 \right]\cup \left[ 4;+\infty \right)$. Ta có: ${y}’=\frac{2x-4}{2\sqrt{{{x}^{2}}-4x}}=0\Leftrightarrow x=2$
Bảng biến thiên (xét dấu ${y}’$):

Vậy hàm số đồng biến trên khoảng $\left( 4;+\infty \right)$, hàm số nghịch biến trên khoảng $\left( -\infty ;0 \right)$.
b) TXĐ: $D=\left( -\infty ;2 \right]\cup \left[ 6;+\infty \right)$
Ta có: ${y}’=\frac{2x-8}{2\sqrt{{{x}^{2}}-8x+12}}=0\text{ }\Leftrightarrow x=4$.
Bảng biến thiên (xét dấu ${y}’$):

Vậy hàm số đồng biến trên khoảng $\left( 6;+\infty \right)$, hàm số nghịch biến trên khoảng $\left( -\infty ;2 \right)$.
| Bài tập 7: Tìm các khoảng đồng biến và nghịch biến của các hàm số sau
a) $y=x+1-2\sqrt{{{x}^{2}}+3x+3}$ b) $y=2x+1-\sqrt{2{{x}^{2}}-8}$ |
Lời giải chi tiết
a) TXĐ: $D=\mathbb{R}$
Ta có: ${y}’=1-\frac{2\left( 2x+3 \right)}{2\sqrt{{{x}^{2}}+2x+3}}=\frac{\sqrt{{{x}^{2}}+2x+3}-\left( 2x+3 \right)}{\sqrt{{{x}^{2}}+2x+3}}=0\Leftrightarrow \sqrt{{{x}^{2}}+2x+3}=2x+3$
$\Leftrightarrow \left\{ \begin{array} {} 2x+3\ge 0 \\ {} {{x}^{2}}+2x+3=4{{x}^{2}}+12x+9 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} 2x\ge -3 \\ {} \left[ \begin{array} {} x=-1 \\ {} x=-2 \\ \end{array} \right. \\ \end{array} \right.\Leftrightarrow x=-1$
Bảng biến thiên (xét dấu ![]() ):
):
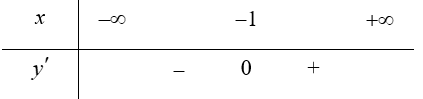
Vậy hàm số đồng biến trên khoảng $\left( -1;+\infty \right)$ và nghịch biến trên khoảng $\left( -\infty ;-1 \right)$.
b) TXĐ: $D=\left( -\infty ;-2 \right]\cup \left[ 2;+\infty \right)$
Ta có: ${y}’=2-\frac{4x}{2\sqrt{2{{x}^{2}}-8}}=\frac{2\sqrt{2{{x}^{2}}-8}-2x}{\sqrt{2{{x}^{2}}-8}}=0\Leftrightarrow \sqrt{2{{x}^{2}}-8}=2x\Leftrightarrow \left\{ \begin{array} {} x\ge 0 \\ {} 2{{x}^{2}}-8=4{{x}^{2}} \\ \end{array} \right.$ (vô nghiệm).
Bảng biến thiên (xét dấu ![]() ):
):

Vậy hàm số đồng biến trên các khoảng $\left( -\infty ;-2 \right)$ và $\left( 2;+\infty \right)$.
| Bài tập 8: Tìm các khoảng đồng biến và nghịch biến của các hàm số sau
a) $y=f\left( x \right)$ biết ${f}’\left( x \right)=x{{\left( x-1 \right)}^{2}}{{\left( x+3 \right)}^{3}},\text{ }\forall x\in \mathbb{R}$. b) $y=g\left( x \right)$ biết ${g}’\left( x \right)=\left( {{x}^{2}}-1 \right)\left( x-2 \right){{\left( x+3 \right)}^{2018}},\text{ }\forall x\in \mathbb{R}$. |
Lời giải chi tiết
a) Bảng biến thiên (xét dấu ${y}’$):
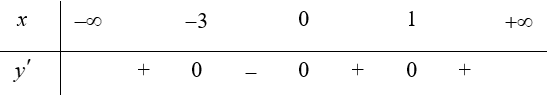
Hàm số đồng biến trên các khoảng $\left( -\infty ;-3 \right)$ và $\left( 0;+\infty \right)$, hàm số nghịch biến trên khoảng $\left( -3;0 \right)$.
b) Ta có: ${g}’\left( x \right)=\left( {{x}^{2}}-1 \right)\left( x-2 \right){{\left( x+3 \right)}^{2018}}={{\left( x+3 \right)}^{2018}}\left( x+2 \right)\left( x+1 \right)\left( x-1 \right)$
Bảng biến thiên (xét dấu ${y}’$):
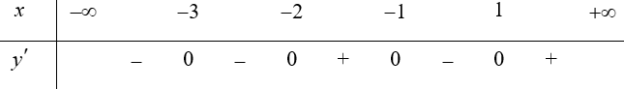
Hàm số đồng biến trên các khoảng $\left( -2;-1 \right)$ và $\left( 1;+\infty \right)$, hàm số nghịch biến trên khoảng$\left( -\infty ;-2 \right)$ và $\left( -1;1 \right)$.
| Bài tập 9: Cho hàm số $y=f\left( x \right)$ có bảng xét dấu đạo hàm sau:
Mệnh đề nào dưới đây đúng? A. Hàm số đồng biến trên khoảng $\left( -2;0 \right)$. B. Hàm số đồng biến trên khoảng $\left( -\infty ;0 \right)$. C. Hàm số nghịch biến trên khoảng $\left( 0;2 \right)$. D. Hàm số nghịch biến trên khoảng $\left( -\infty ;-2 \right)$. |
Lời giải chi tiết
Hàm số nghịch biến trên các khoảng $\left( -2;0 \right)$; $\left( 0;2 \right)$.
Và đồng biến trên các khoảng $\left( -\infty ;-2 \right)$ và $\left( 2;+\infty \right)$. Chọn C.
| Bài tập 10: Tìm tất cả các khoảng đồng biến của hàm số $y=\frac{-{{x}^{2}}+2x-1}{x+2}$.
A. $\left( -5;-2 \right)$ và $\left( -2;1 \right)$ B. $\left( -5;-2 \right)$ và $\left( 1;+\infty \right)$ C. $\left( -\infty ;-2 \right)$ và $\left( -2;1 \right)$ D. $\left( -\infty ;-2 \right)$ và $\left( 1;+\infty \right)$ |
Lời giải chi tiết
Ta có: ${y}’=\frac{\left( -2x+2 \right)\left( x+2 \right)-\left( -{{x}^{2}}+2x-1 \right)}{{{\left( x+2 \right)}^{2}}}=\frac{-{{x}^{2}}-4x+5}{{{\left( x+2 \right)}^{2}}}=0\Leftrightarrow \left\{ \begin{array} {} x=1 \\ {} x=-5 \\ \end{array} \right.$.
Bảng biến thiên (xét dấu ![]() ):
):

Do đó, hàm số đồng biến trên các khoảng $\left( -5;-2 \right)$ và $\left( -2;1 \right)$. Chọn A.
| Bài tập 11: Tìm tất cả các khoảng nghịch biến của hàm số $y=-{{x}^{3}}-3{{x}^{2}}+24x+1$.
A. $\left( -4;2 \right)$ B. $\left( -4;0 \right)$ và $\left( 2;+\infty \right)$ C. $\left( -\infty ;-4 \right)$ và $\left( 0;2 \right)$ D. $\left( -\infty ;-4 \right)$ và $\left( 2;+\infty \right)$ |
Lời giải chi tiết
Ta có: ${y}’=-3{{x}^{2}}-6x+24=0\Leftrightarrow \left\{ \begin{array} {} x=-4 \\ {} x=2 \\ \end{array} \right.$.
Bảng biến thiên (xét dấu ${y}’$):
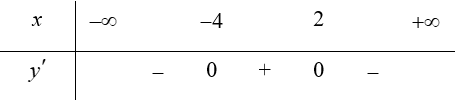
Do đó, hàm số nghịch biến trên các khoảng $\left( -\infty ;-4 \right)$ và $\left( 2;+\infty \right)$. Chọn D.
| Bài tập 12: Hàm số $y=\sqrt{{{x}^{2}}-2x}$
A. Đồng biến trên $\left( 2;+\infty \right)$ và nghịch biến trên $\left( -\infty ;0 \right)$. B. Đồng biến trên $\left( -\infty ;0 \right)$ và nghịch biến trên $\left( 2;+\infty \right)$. C. Đồng biến trên $\left( 1;+\infty \right)$ và nghịch biến trên $\left( -\infty ;1 \right)$. D. Đồng biến trên $\left( 1;2 \right)$ và nghịch biến trên $\left( 0;1 \right)$. |
Lời giải chi tiết
TXĐ: $D=\left( -\infty ;0 \right]\cup \left[ 2;+\infty \right)$. Ta có: ${y}’=\frac{2x-2}{2\sqrt{{{x}^{2}}-2x}}=0\Leftrightarrow x=2$
Bảng biến thiên (xét dấu ${y}’$):

Do vậy hàm số đồng biến trên $\left( 2;+\infty \right)$ và nghịch biến trên $\left( -\infty ;0 \right)$. Chọn A.
| Bài tập 13: Hàm số $y=x\sqrt{1-{{x}^{2}}}$
A. Đồng biến trên các khoảng $\left( -1;\frac{\sqrt{2}}{2} \right)$ và $\left( \frac{\sqrt{2}}{2};1 \right)$ và nghịch biến trên $\left( \frac{-\sqrt{2}}{2};\frac{\sqrt{2}}{2} \right)$. B. Đồng biến trên $\left( \frac{-\sqrt{2}}{2};\frac{\sqrt{2}}{2} \right)$ và nghịch biến trên các khoảng $\left( -1;\frac{\sqrt{2}}{2} \right)$ và $\left( \frac{\sqrt{2}}{2};1 \right)$. C. Đồng biến trên $\left( \frac{-\sqrt{2}}{2};\frac{\sqrt{2}}{2} \right)$ và nghịch biến trên các khoảng $\left( -\infty ;-\frac{\sqrt{2}}{2} \right)$ và $\left( \frac{\sqrt{2}}{2};+\infty \right)$. D. Đồng biến trên $\left( \frac{-\sqrt{2}}{2};\frac{\sqrt{2}}{2} \right)$ và nghịch biến trên các khoảng $\left( -\infty ;-1 \right)$ và $\left( 1;+\infty \right)$. |
Lời giải chi tiết
TXĐ: $D=\left[ -1;1 \right]$.
Ta có: ${y}’=\sqrt{1-{{x}^{2}}}-\frac{{{x}^{2}}}{\sqrt{1-{{x}^{2}}}}=\frac{1-2{{x}^{2}}}{\sqrt{1-{{x}^{2}}}}$.
Lập bảng xét dấu ${y}’$:
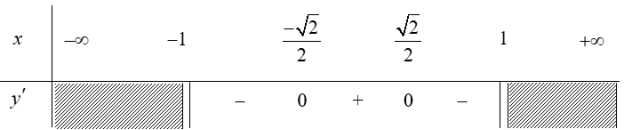
Do đó hàm số đồng biến trên $\left( \frac{-\sqrt{2}}{2};\frac{\sqrt{2}}{2} \right)$ và nghịch biến trên các khoảng $\left( -1;\frac{\sqrt{2}}{2} \right)$ và $\left( \frac{\sqrt{2}}{2};1 \right)$.
Chọn B.
| Bài tập 14: Hàm số $y=\frac{x-2}{{{x}^{2}}+x+1}$ đồng biến trên:
A. $\mathbb{R}$. B. $\left( -\infty ;2-\sqrt{7} \right)$ và $\left( 2+\sqrt{7};+\infty \right)$ C. $\left( 2-\sqrt{7};2+\sqrt{7} \right)$ D. Hàm số đã cho luôn nghịch biến trên $\mathbb{R}$. |
Lời giải chi tiết
TXĐ: $D=\mathbb{R}$.
Ta có: ${y}’=\frac{-{{x}^{2}}+4x+3}{{{\left( {{x}^{2}}+x+1 \right)}^{2}}}>0\Leftrightarrow {{x}^{2}}-4x-3<0\Leftrightarrow 2-\sqrt{7}<x<2+\sqrt{7}$. Chọn C.
| Bài tập 15: Cho hàm số $y=\frac{2x-1}{{{\left( x-1 \right)}^{2}}}$. Hàm số đã cho:
A. Đồng biến trên các khoảng $\left( -\infty ;0 \right)$ và $\left( 1;+\infty \right)$ và nghịch biến trên khoảng $\left( 0;1 \right)$. B. Đồng biến trên khoảng $\left( 0;1 \right)$ và nghịch biến trên các khoảng $\left( -\infty ;0 \right)$ và $\left( 1;+\infty \right)$. C. Đồng biến trên khoảng $\left( -\infty ;0 \right)$ và nghịch biến trên khoảng $\left( 1;+\infty \right)$. D. Đồng biến trên khoảng $\left( 1;+\infty \right)$ và nghịch biến trên khoảng $\left( -\infty ;0 \right)$. |
Lời giải chi tiết
TXĐ: $D=\mathbb{R}\backslash \left\{ 1 \right\}$.
Ta có: ${y}’=\frac{2{{\left( x-1 \right)}^{2}}-2\left( x-1 \right)\left( 2x-1 \right)}{{{\left( x-1 \right)}^{4}}}=\frac{2\left( x-1 \right)-2\left( 2x-1 \right)}{{{\left( x-1 \right)}^{3}}}=\frac{-2x}{{{\left( x-1 \right)}^{3}}}$.
Lập bảng xét dấu của${y}’$:
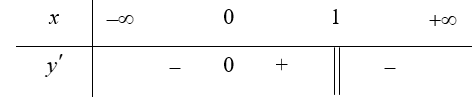
Do vậy hàm số đồng biến trên khoảng $\left( 0;1 \right)$ và nghịch biến trên các khoảng $\left( -\infty ;0 \right)$ và $\left( 1;+\infty \right)$. Chọn B.
| Bài tập 16: Cho hàm số $y=\frac{3x-2}{{{\left( x-2 \right)}^{2}}}$. Hàm số đã cho:
A. Đồng biến trên các khoảng $\left( -\infty ;\frac{-2}{3} \right)$ và $\left( 2;+\infty \right)$ và nghịch biến trên khoảng $\left( \frac{-2}{3};2 \right)$. B. Đồng biến trên khoảng $\left( \frac{-2}{3};2 \right)$ và nghịch biến trên các khoảng $\left( -\infty ;-\frac{2}{3} \right)$ và $\left( 2;+\infty \right)$. C. Đồng biến trên khoảng $\left( -\infty ;-\frac{2}{3} \right)$ và nghịch biến trên khoảng $\left( 2;+\infty \right)$. D. Đồng biến trên khoảng $\left( 2;+\infty \right)$ và nghịch biến trên khoảng $\left( -\infty ;\frac{-2}{3} \right)$. |
Lời giải chi tiết
TXĐ: $D=\mathbb{R}\backslash \left\{ 2 \right\}$.
Ta có: ${y}’=\frac{3{{\left( x-2 \right)}^{2}}-2\left( x-2 \right)\left( 3x-2 \right)}{{{\left( x-2 \right)}^{4}}}=\frac{3\left( x-2 \right)-2\left( 3x-2 \right)}{{{\left( x-2 \right)}^{3}}}=\frac{-3x-2}{{{\left( x-2 \right)}^{3}}}$.
Lập bảng xét dấu ${y}’$:
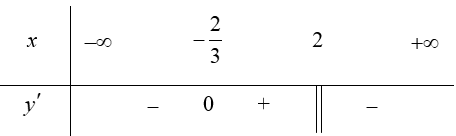
Do đó hàm số đồng biến trên khoảng $\left( \frac{-2}{3};2 \right)$ và nghịch biến trên các khoảng $\left( -\infty ;-\frac{2}{3} \right)$ và $\left( 2;+\infty \right)$.
Chọn B.
| Bài tập 17: Cho hàm số $y=x\sqrt{3-x}$ nghịch biến trên khoảng:
A. $\left( -\infty ;3 \right)$. B. $\left( -\infty ;2 \right)$. C. $\left( 2;3 \right)$. D. $\left( 2;+\infty \right)$. |
Lời giải chi tiết
TXĐ: $D=\left( -\infty ;3 \right]$.
Ta có: ${y}’=\sqrt{3-x}+x.\frac{-1}{2\sqrt{3-x}}=\frac{6-2x-x}{2\sqrt{3-x}}=\frac{6-3x}{2\sqrt{3-x}}=0\Leftrightarrow x=2$.
Lập bảng xét dấu ${y}’$:
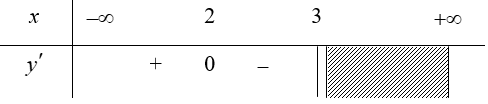
Do đó hàm số nghịch biến trên khoảng $\left( 2;3 \right)$. Chọn C.

