CÔNG THỨC CỰC TRỊ CỦA HÀM BẬC 4 TRÙNG PHƯƠNG GIẢI NHANH
Một số công thức tính cực đại cực tiểu hàm trùng phương
R Xét hàm số trùng phương $y=a{{x}^{4}}+b{{x}^{2}}+c$ với hệ số $a\ne 0$.
Ta có: $y’=4a{{x}^{3}}+2bx=0\Leftrightarrow \left[ \begin{matrix} x=0\text{ } \\ {{x}^{2}}=\frac{-b}{2a} \\\end{matrix}. \right.$ Khi đó:
Hàm số có một cực trị $\Leftrightarrow \frac{-b}{2a}\ge 0\Leftrightarrow ab\ge 0.$
Hàm số có ba cực trị $\Leftrightarrow \frac{-b}{2a}<0\Leftrightarrow ab<0.$
Hàm số có một cực trị và cực trị là cực tiểu $\Leftrightarrow \left\{ \begin{matrix} a>0 \\ b\ge 0 \\\end{matrix} \right..$
Hàm số có một cực trị và cực trị là cực đại $\Leftrightarrow \left\{ \begin{matrix} a>0 \\ b\le 0 \\\end{matrix} \right..$
Hàm số có hai cực tiểu và một cực đại $\Leftrightarrow \left\{ \begin{matrix} a>0 \\ b<0 \\\end{matrix} \right..$
Hàm số có hai cực đại và một cực tiểu $\Leftrightarrow \left\{ \begin{matrix} a>0 \\ b>0 \\\end{matrix} \right..$
R Bài toán hàm trùng phương có ba cực trị tạo tam giác ABC (rất hay gặp)
Tìm điều kiện tồn tại ba điểm cực trị: $\frac{-b}{2a}>0\left( * \right)$
Với điều kiện (*) ta có \(y’=0\Leftrightarrow \left[ \begin{matrix} x=0={{x}_{A}}\xrightarrow{{}}{{y}_{A}}\text{ } \\ {{x}_{2}}=\sqrt{\frac{-b}{2a}}={{x}_{B}}\xrightarrow{{}}{{y}_{B}} \\ {{x}_{3}}=-\sqrt{\frac{-b}{2a}}={{x}_{C}}\xrightarrow{{}}{{y}_{C}} \\\end{matrix} \right.,\) từ đó
\(A\left( 0;{{y}_{A}} \right);B\left( \sqrt{\frac{-b}{2a}};{{y}_{B}} \right);C\left( -\sqrt{\frac{-b}{2a}};{{y}_{C}} \right)\)
Do hàm chẵn với x nên các điểm B, C có ${{y}_{B}}={{y}_{C}}.$
Nhận xét: $A\in Oy,B;C$ đối xứng nhau qua Oy nên tam giác ABC luôn là tam giác cân tại A.
Ta xét một số tính chất cơ bản thường gặp của hàm số:
Tính chất 1: 3 điểm cực trị tạo thành một tam giác vuông cân.
Tính chất 2: 3 điểm cực trị tạo thành một tam giác đều.
Do tam giác ABC đã cân tại A nên chỉ có thể vuông cân tại đỉnh A. Khi đó ta có điều kiện $\overrightarrow{AB}.\overrightarrow{AC}=0,(1)$ với $\overrightarrow{AB}=\left( \sqrt{\frac{-b}{2a}};{{y}_{B}}-{{y}_{A}} \right);\overrightarrow{AC}=\left( -\sqrt{\frac{-b}{2a}};{{y}_{C}}-{{y}_{A}} \right)$
Từ đó (1)$\Leftrightarrow \overrightarrow{AB}.\overrightarrow{AC}=0\Leftrightarrow \frac{b}{2a}+{{\left( {{y}_{B}}-{{y}_{A}} \right)}^{2}}=0$
Giá trị m tìm được kết hợp với điều kiện tồn tại ở (*) cho ta kết quả cuối cùng của bài toán.
Ngoài ra ta cũng có thể dùng điều kiện Pitago cho tam giác cân ABC: $A{{B}^{2}}+A{{C}^{2}}=B{{C}^{2}}\Leftrightarrow 2A{{B}^{2}}=B{{C}^{2}}$
Tính chất 3: 3 điểm cực trị tạo thành một tam giác có một góc bằng ${{120}^{0}}.$
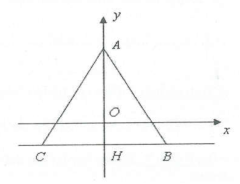
Tam giác ABC cân tại A nên $\overset\frown{BAC}={{120}^{0}}.$ Gọi H là trung điểm của $BC\Rightarrow H\left( 0;{{y}_{B}} \right).$
Ta có $\cos \overset\frown{HAB}=\frac{AH}{AB}\Leftrightarrow \cos {{60}^{0}}=\frac{AH}{AB}\Leftrightarrow AB=2AH\Leftrightarrow A{{B}^{2}}=4A{{H}^{2}},(3)$
với $\overrightarrow{AB}=\left( \sqrt{\frac{-b}{2a}};{{y}_{B}}-{{y}_{A}} \right);\overrightarrow{AH}=\left( 0;{{y}_{B}}-{{y}_{A}} \right)$, từ đó (3) $\Leftrightarrow \frac{-b}{2a}+{{\left( {{y}_{B}}-{{y}_{A}} \right)}^{2}}=4{{\left( {{y}_{B}}-{{y}_{A}} \right)}^{2}}$
Giá trị m tìm được kết hợp với điều kiện tồn tại ở (*) cho ta kết quả cuối cùng của bài toán.
Tính chất 4: 3 điểm cực trị tạo thành một tam giác có diện tích $S={{S}_{o}}$ cho trước.
Gọi H là trung điểm của $BC\Rightarrow H\left( 0;{{y}_{B}} \right).$ Khi đó
${{S}_{\Delta ABC}}=\frac{1}{2}AH.BC\Leftrightarrow 2{{S}_{o}}=AH.BC\Leftrightarrow 4S_{o}^{2}=A{{H}^{2}}.B{{C}^{2}},(4)$
với $\overrightarrow{BC}=\left( -2\sqrt{\frac{-b}{2a}};0 \right);\overrightarrow{AH}=\left( 0;{{y}_{B}}-{{y}_{A}} \right)$, từ đó (4) $\Leftrightarrow 4S_{o}^{2}={{\left( {{y}_{B}}-{{y}_{A}} \right)}^{2}}.4\left( \frac{-b}{2a} \right)$
Giá trị m tìm được kết hợp với điều kiện tồn tại ở (*) cho ta kết quả cuối cùng của bài toán.
Tính chất 5: 3 điểm cực trị tạo thành một tam giác có bán kính đường tròn ngoại tiếp R cho trước.
Sử dụng công thức diện tích tam giác $S=\frac{abc}{4R}\Rightarrow R=\frac{abc}{4S}\Leftrightarrow R=\frac{AB.AC.BC}{4.\frac{1}{2}.AH.BC}\Leftrightarrow R=\frac{A{{B}^{2}}}{2AH}$
Giải phương trình trên ta được giá trị của m, đối chiếu với (*) cho ta kết luận cuối cùng.
Tính chất 6: 3 điểm cực trị tạo thành một tam giác có trọng tâm $G\left( 0;\alpha \right)$ cho trước.
Ta có điều kiện trong trường hợp này là $\alpha =\frac{{{y}_{A}}+{{y}_{B}}+{{y}_{C}}}{3}\Leftrightarrow {{y}_{A}}+2{{y}_{B}}=3\alpha $
Tính chất 7: 3 điểm cực trị tạo thành một tam giác có bán kính đường tròn nội tiếp r cho trước.
Sử dụng công thức diện tích tam giác $S=p.r\Rightarrow r=\frac{S}{p}=\frac{\frac{1}{2}AH.BC}{\frac{AB+AC+BC}{2}}=\frac{AH.BC}{2AB+BC}$
Giải phương trình trên ta được giá trị của m, đối chiếu với (*) cho ta kết luận cuối cùng.
R Một số công thức tính nhanh liên quan đến cực trị của hàm trùng phương (tham khảo)
Xét hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$ với $a\ne 0$ và hàm số có ba điểm cực trị.
Khi đó gọi $A\left( 0;c \right);B\left( \sqrt{\frac{-b}{2a}};-\frac{\Delta }{4a} \right);C\left( -\sqrt{\frac{-b}{2a}};-\frac{\Delta }{4a} \right)$ lần lượt là ba điểm cực trị của đồ thị hàm số $\Rightarrow AB=AC=\sqrt{\frac{{{b}^{4}}}{16{{a}^{2}}}-\frac{b}{2a}};BC=2\sqrt{-\frac{b}{2a}}$ với $\Delta ={{b}^{2}}-4ac$.
Xét $\Delta ABC$ cân, đặt $\overset\frown{BAC}=\alpha $ ta có ${{\tan }^{2}}\frac{\alpha }{2}=-\frac{8a}{{{b}^{3}}}.$
Và diện tích $S=\frac{1}{4}.\frac{{{b}^{2}}}{\left| a \right|}.\sqrt{\frac{-b}{2a}}\Rightarrow {{S}^{2}}=\frac{-{{b}^{5}}}{32{{a}^{3}}},$ phương trình đường tròn đi qua ba điểm A, B, C là
${{x}^{2}}+{{y}^{2}}-\left( c+n \right)x+c.n=0$ với $n=\frac{2}{b}-\frac{\Delta }{4a}$.
Đồ thị hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\text{ }\left( ab<0 \right)$ có ba điểm cực trị $A\in Oy,B,C$ tạo thành
Bảng công tính nhanh tính đơn điệu của hàm số
|
DỮ KIỆN GIẢ THIẾT |
CÔNG THỨC TÍNH NHANH |
|
Tam giác ABC vuông cân tại A |
$\alpha ={{90}^{0}}$ |
|
Tam giác ABC đều |
$\alpha ={{60}^{0}}$ |
|
$\overset\frown{BAC}=\alpha $ |
${{\tan }^{2}}\frac{\alpha }{2}=-\frac{8a}{{{b}^{3}}}$ |
|
${{S}_{\Delta ABC}}={{S}_{o}}$ |
${{\left( {{S}_{o}} \right)}^{2}}=\frac{-{{b}^{5}}}{32{{a}^{3}}}$ |
|
${{r}_{\Delta ABC}}={{r}_{o}}$ (bán kính đường tròn nội tiếp) |
${{r}_{o}}=\frac{{{b}^{2}}}{\left| a \right|\left( 1+\sqrt{1-\frac{{{b}^{2}}}{a}} \right)}$ |
|
$BC={{m}_{0}}$ |
$a.m_{0}^{2}+2b=0$ |
|
$Ab=AC={{n}_{0}}$ |
$16{{a}^{2}}.n_{0}^{2}-{{b}^{4}}+8b=0$ |
|
$B,C\in Ox$ (ba điểm cực trị nằm trên cùng một trục tọa độ) |
${{b}^{2}}-4ac=0$ |
|
Tam giác có trọng tâm $O\left( 0;0 \right)$ (gốc tọa độ) |
${{b}^{2}}-6ac=0$ |
|
Tam giác có trực tâm $O\left( 0;0 \right)$ (gốc tọa độ) |
${{b}^{3}}+8a-4ac=0$ |
|
${{R}_{\Delta ABC}}={{R}_{0}}$ (bán kính đường tròn ngoại tiếp) |
\({{R}_{0}}=\frac{{{b}^{3}}-8a}{8\left| a \right|b}\) |
