Tìm các khoảng đồng biến, nghịch biến của hàm số dựa vào đồ thị và bảng biến thiên
Phương pháp giải đồng biến nghịch biến – đơn điệu hàm số
Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải, nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.
Chú ý tập xác định của hàm số.
Bài tập xét tính đồng biên nghịch biến
|
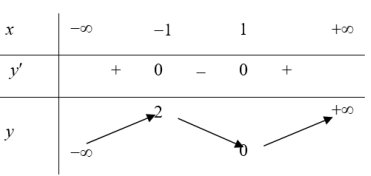
Ví dụ 1: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ Khẳng định nào sau đây là đúng. A. Hàm số đồng biến trên khoảng $\left( -\infty ;2 \right)$. B. Hàm số nghịch biến trên khoảng $\left( -1;0 \right)$. C. Hàm số nghịch biến trên khoảng $\left( 0;2 \right)$. D. Hàm số đồng biến trên $\mathbb{R}$. |
Lời giải chi tiết
Dựa vào bảng biến thiên ta thấy: Hàm số nghịch biến trên khoảng $\left( -1;1 \right)$ và đồng biến trên các khoảng $\left( -\infty ;-1 \right)$ và $\left( 1;+\infty \right)$ Þ Hàm số nghịch biến trên khoảng $\left( -1;0 \right)$. Chọn B.
|
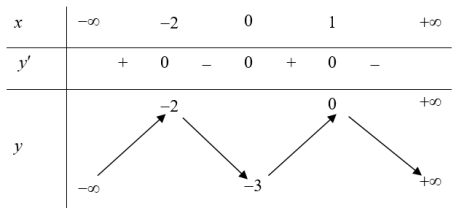
Ví dụ 2: Cho hàm số Khẳng định nào sau đây là đúng. A. Hàm số đồng biến trên khoảng $\left( -\infty ;-2 \right)$và$\left( -3;0 \right)$. B. Hàm số nghịch biến trên khoảng $\left( -3;-2 \right)$. C. Hàm số đồng biến trên khoảng $\left( 0;1 \right)$. D. Hàm số nghịch biến trên khoảng $\left( 0;+\infty \right)$. |
Lời giải chi tiết
Dựa vào bảng biến thiên ta thấy: Hàm số đồng biến trên các khoảng $\left( -\infty ;2 \right)$và $\left( 0;1 \right)$.
Hàm số nghịch biến trên các khoảng $\left( -2;0 \right)$ và $\left( 1;+\infty \right)$. Chọn B.
|
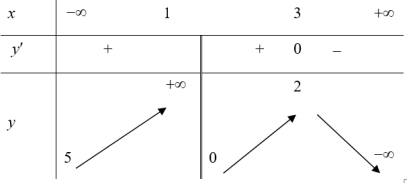
Ví dụ 3: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng. A. Hàm số đồng biến trên khoảng $\left( -\infty ;3 \right)$. B. Hàm số nghịch biến trên khoảng $\left( 2;+\infty \right)$. C. Hàm số đồng biến trên $\left( -\infty ;1 \right)\cup \left( 1;3 \right)$. D. Hàm số đồng biến trên $\left( -\infty ;1 \right)$ và $\left( 1;3 \right)$. |
Lời giải chi tiết
Hàm số xác định trên tập $\mathbb{R}\backslash \left\{ 1 \right\}$.
Dựa vào bảng biến thiên suy ra hàm số đồng biến trên các khoảng $\left( -\infty ;1 \right)$ và $\left( 1;3 \right)$. Hàm số nghịch biến trên khoảng $\left( 3;+\infty \right)$. Chọn D.
|
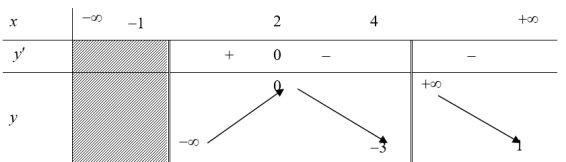
Ví dụ 4: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ Khẳng định nào sau đây đúng. A. Hàm số đồng biến trên khoảng $\left( -\infty ;2 \right)$. B. Hàm số nghịch biến trên khoảng $\left( 2;+\infty \right)$. C. Hàm số nghịch biến trên mỗi khoảng $\left( 2;4 \right)$ và $\left( 4;+\infty \right)$. D. Hàm số đồng biến trên khoảng $\left( -\infty ;0 \right)$. |
Lời giải chi tiết
Tập xác định của hàm số là: $\left( -1;+\infty \right)\backslash \left\{ 4 \right\}$.
Dựa vào bảng biến thiên suy ra hàm số đồng biến trên khoảng $\left( -1;2 \right)$ và nghịch biến trên mỗi khoảng $\left( 2;4 \right)$ và $\left( 4;+\infty \right)$. Chọn C.
|
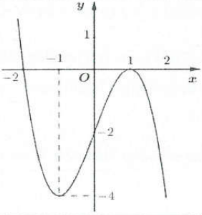
Ví dụ 5: Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng. A. $\left( -1;1 \right)$ B. $\left( -\infty ;-2 \right)$ C. $\left( 1;+\infty \right)$ D. $\left( -2;1 \right)$ |
Lời giải chi tiết
Dựa vào đồ thị hàm số suy ra hàm số đồng biến trên khoảng $\left( -1;1 \right)$ và nghịch biến trên các khoảng $\left( -\infty ;-1 \right)$ và $\left( 1;+\infty \right)$. Chọn A.
|
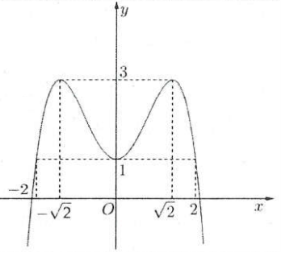
Ví dụ 6: Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng. A. $\left( -\sqrt{2};\sqrt{2} \right)$. B. $\left( -2;2 \right)$. C. $\left( 1;3 \right)$. D. $\left( 0;\sqrt{2} \right)$. |
Lời giải chi tiết
Dựa vào đồ thị hàm số suy ra hàm số đồng biến trên khoảng $\left( -\infty ;-\sqrt{2} \right),\left( 0;\sqrt{2} \right)$ và nghịch biến trên các khoảng $\left( -\sqrt{2};0 \right)$ và $\left( \sqrt{2};+\infty \right)$. Chọn D.