Bài tập Tìm tiệm cận của đồ thị hàm số dựa vào đồ thị hàm số có đáp án
Phương pháp giải cho đồ thị tìm tiệm cận đứng tiệm cận ngang
▪ Dựa vào đồ thị hàm số để xác định nghiệm của mẫu số và tử số từ đó suy ra các đường tiệm cận đứng của đồ thị hàm số.
▪ Tìm các giới hạn $\underset{x\to \pm \infty }{\mathop{\lim }}\,y$ để tìm các đường tiệm cận ngang của đồ thị hàm số.
Bài tập trắc nghiệm về tiệm cận có đáp án
|
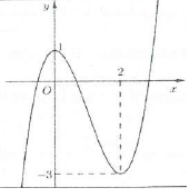
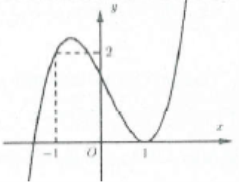
Bài tập 1: Cho đồ thị hàm số $y=f\left( x \right)$ như hình vẽ bên. Số đường tiệm cận đứng của đồ thị hàm số $y=\frac{x-2}{f\left( x \right)+3}$ là: A. 1. B. 2. C. 3. D. 4. |
Lời giải chi tiết
Dựa vào đồ thị hàm số ta thấy phương trình $f\left( x \right)+3=0\Leftrightarrow f\left( x \right)=-3$ có nghiệm kép $x=2$ và một nghiệm $x=a<0$ .
Do đó $y=\frac{x-2}{f\left( x \right)+3}=\frac{x-2}{k\left( x-a \right).{{\left( x-2 \right)}^{2}}}\Rightarrow $ Đồ thị hàm số $y=\frac{x-2}{f\left( x \right)+3}$ có 2 đường tiệm cận đứng là $x=a$ và $x=2$. Chọn B.
|
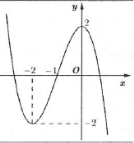
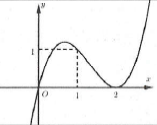
Bài tập 2: Cho đồ thị hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$ như hình vẽ bên. Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số $y=\frac{{{x}^{2}}+2x}{f\left( x \right)+2}$ là A. 1. B. 2. C. 3. D. 4. |
Lời giải chi tiết
Dựa vào đồ thị dễ thấy hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có $a\ne 0$.
Ta có: $\underset{x\to \infty }{\mathop{\lim }}\,\frac{{{x}^{2}}-4}{f\left( x \right)+2}=0\Rightarrow y=0$ là tiệm cận ngang của đồ thị hàm số
Phương trình $f\left( x \right)=-2$ có nghiệm kép $x=-2$ và một nghiệm $x>0$
Phương trình ${{x}^{2}}+2x=0\Leftrightarrow \left[ \begin{array} {} x=-2 \\ {} x=0 \\ \end{array} \right.$ do đó đồ thị hàm số $y=\frac{{{x}^{2}}+2x}{f\left( x \right)+2}$ có 2 đường tiệm cận đứng.
Vậy đồ thị hàm số có 3 đường tiệm cận. Chọn C.
|
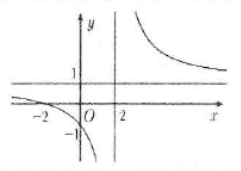
Bài tập 3: Cho hàm số $y=\frac{ax+2}{cx+b}$ có đồ thị (C) như hình vẽ bên. Tính tổng $T=a+2b+3c$. A. $T=0.$ B. $T=-1.$ C. $T=3.$ D. $T=2.$ |
Lời giải chi tiết
Từ hình vẽ, ta có nhận xét sau:
Đường thẳng $x=2$ là tiệm cận đứng của đồ thị $\left( C \right)\Rightarrow x=-\frac{b}{c}=2\Leftrightarrow b=-2c.$
Đường thẳng $y=1$ là tiệm cận ngang của đồ thị $\left( C \right)\Rightarrow x=\frac{a}{c}=1\Leftrightarrow a=c$.
Điểm $M\left( 0;-1 \right)\in \left( C \right)$ suy ra $y\left( 0 \right)=-1\Leftrightarrow \frac{2}{b}=-1\Leftrightarrow b=-2$.
Suy ra $\left\{ \begin{array} {} b=-2 \\ {} b=-2c=-2\text{a} \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} a=1 \\ {} b=-2 \\ {} c=1 \\ \end{array} \right.\Rightarrow T=a+2b+3c=1+2.\left( -2 \right)+3=0$. Chọn A.
|
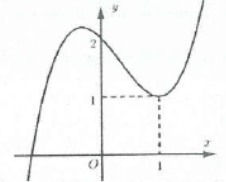
Bài tập 4: Cho hàm số bậc 3 có đồ thị như hình vẽ bên. Số tiệm cận đứng của đồ thị hàm số $y=\frac{{{x}^{2}}-x}{{{f}^{2}}\left( x \right)-3f\left( x \right)+2}$ là: A. 3. B. 4. C. 5. D. 6. |
Lời giải chi tiết
Điều kiện: $\left\{ \begin{array} {} f\left( x \right)-1\ne 0 \\ {} f\left( x \right)-2\ne 0 \\ \end{array} \right..$ Ta có: $y=\frac{x\left( x-1 \right)}{\left[ f\left( x \right)-1 \right]\left[ f\left( x \right)-2 \right]}$
Phương trình $f\left( x \right)-1=0$ có nghiệm kép $x=1$ và $x={{x}_{1}}<0\Rightarrow $ Đồ thị hàm số có tiệm cận đứng $x=1,\,\,x={{x}_{1}}$.
Phương trình $f\left( x \right)-2=0$ có nghiệm $x=0$ và $x={{x}_{2}}1$ suy ra đồ thị hàm số có tiệm cận đứng $x={{x}_{2}}$ và $x={{x}_{3}}$.
Do đó đồ thị hàm số có 4 đường tiệm cận đứng. Chọn B.
|
Bài tập 5: Cho hàm số bậc 3 có đồ thị như hình vẽ bên. Số tiệm cận đứng của đồ thị hàm số $y=\frac{\left( {{x}^{2}}-1 \right)\sqrt{{{x}^{2}}+x}}{x\left[ {{f}^{2}}\left( x \right)-2f\left( x \right) \right]}$ là: A. 3. B. 4. C. 5. D. 6. |
Lời giải chi tiết
Điều kiện: $\left\{ \begin{array} {} x\ge -1 \\ {} x<0 \\ {} {{f}^{2}}\left( x \right)-2f\left( x \right)\ne 0 \\ \end{array} \right..$
Ta có: $y=\frac{\left( {{x}^{2}}-1 \right)\sqrt{{{x}^{2}}+x}}{x\left[ {{f}^{2}}\left( x \right)-2f\left( x \right) \right]}=\sqrt{\frac{x+1}{x}}.\frac{\left( x-1 \right)\left( x+1 \right)}{f\left( x \right)\left[ f\left( x \right)-2 \right]}$
Đồ thị hàm số có tiệm cận đứng $x=0$.
Phương trình $f\left( x \right)=0$ có nghiệm kép $x=1$ và $x={{x}_{1}}<-1$ suy ra đồ thị hàm số có tiệm cận đứng $x=1$ và $x={{x}_{1}}$.
Phương trình $f\left( x \right)-2=0$ có 3 nghiệm phân biệt trong đó $\left[ \begin{array} {} {{x}_{2}}=-1 \\ {} {{x}_{3}}\in \left( -1;0 \right) \\ {} {{x}_{4}}>1 \\ \end{array} \right.$ do đó đồ thị hàm số có tiệm cận đứng $x={{x}_{4}}$.
Vậy đồ thị hàm số có 4 đường tiệm cận đứng. Chọn B.
|
Bài tập 6: Cho hàm số bậc 3 có đồ thị như hình vẽ bên. Số tiệm cận đứng của đồ thị hàm số $y=\frac{\left( {{x}^{2}}-3\text{x}+2 \right)\sqrt{{{x}^{2}}-x}}{{{f}^{2}}\left( x \right)-f\left( x \right)}$ là: A. 3. B. 4. C. 5. D. 6. |
Lời giải chi tiết
Điều kiện: $\left\{ \begin{array} {} x\ge 1 \\ {} x\le 0 \\ {} {{f}^{2}}\left( x \right)-f\left( x \right)\ne 0 \\ \end{array} \right.$ và $y=\frac{\left( x-1 \right)\left( x-2 \right)\sqrt{x\left( x-1 \right)}}{f\left( x \right)\left[ f\left( x \right)-1 \right]}$
Phương trình $f\left( x \right)=0$ có nghiệm $x=0$ và nghiệm kép $x=2$ nên đồ thị hàm số có tiệm cận đứng $x=0,\,\,x=2$.
Phương trình $f\left( x \right)-1=0$ có 3 nghiệm đơn $\left[ \begin{array} {} x={{x}_{1}}\in \left( 0;1 \right) \\ {} x=1 \\ {} x={{x}_{2}}>2 \\ \end{array} \right.$ suy ra đồ thị hàm số có tiệm cận đứng $x={{x}_{2}}$. Vậy đồ thị hàm số có 3 đường tiệm cận đứng. Chọn A.