Số phức là gì? Các phép toán của số phức, biểu diễn hình học modun số phức
1) Các khái niệm cơ bản: Số phức là gì?
· Định nghĩa: Số phức là số có dạng a + bi, trong đó a và b là những số thực và số i thỏa mãn ${{i}^{2}}=-1$. Kí hiệu số phức đó là z và viết $z=a+bi$.
Trong đó i được gọi là đơn vị ảo, a được gọi là phần thực và b được gọi là phần ảo của số phức $z=a+bi$.
Tập hợp các số phức được kí hiệu là $\mathbb{C}$.
Chú ý:
– Số phức $z=a=a+0.i$ có phần ảo bằng 0 được coi là số thực và viết là $a+0.i=a\in \mathbb{R}$.
– Số phức có phần thực bằng 0 được gọi là số ảo (còn gọi là số thuần ảo): $z=0+bi=bi\left( b\in \mathbb{R} \right)$.
Ví dụ $z=5i$ là số thuần ảo.
– Số $0=0+0.i$ vừa là số thực, vừa là số ảo.
Bài tập: Số phức $z=5+\sqrt{3}i$ có phần thực bằng 5, phần ảo bằng $\sqrt{3}$.
Số phức $z=-4i$ có phần thực bằng 0, phần ảo bằng $-4$; đó là một số thuần ảo.
· Hai số phức $z=a+bi;{z}’={a}’+{b}’i\text{ }\left( a;{a}’;b;{b}’\in \mathbb{R} \right)$ gọi là bằng nhau nếu $\left\{ \begin{array} {} a={a}’ \\ {} b={b}’ \\ \end{array} \right.$.
Khi đó ta viết $z={z}’$.
2) Biểu diễn hình học của số phức
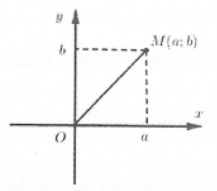Xét mặt phẳng tọa độ Oxy. Mỗi số phức $a+bi\text{ }\left( a;b\in \mathbb{R} \right)$được biểu diễn bởi điểm $M\left( a;b \right)$. Ngược lại, mỗi điểm $M\left( a;b \right)$ biểu diễn một số phức $z=a+bi$. Ta còn viết $M\left( a+bi \right)$ hay đơn giản là $M\left( z \right)$.
Mặt phẳng tọa độ biểu diễn số phức được gọi là mặt phẳng phức. Gốc tọa độ O biểu diễn số 0.
Các điểm trên trục hoành Ox biểu diễn các số thực, do đó trục Ox còn được gọi là trục thực. Các điểm trên trục tung Oy biểu diễn các số ảo, do đó trục Oy còn được gọi là trục ảo.
3) Phép cộng và phép trừ số phức
a) Phép cộng hai số phức
Tổng của hai số phức $z=a+bi;{z}’={a}’+{b}’i\text{ }\left( a;{a}’;b;{b}’\in \mathbb{R} \right)$ là số phức $z+{z}’=a+{a}’+\left( b+{b}’ \right)i$.
Bài tập: $4+i+5-2i=\left( 4+5 \right)+\left( i-2i \right)=9-i$.
$\sqrt{3}+i-2\sqrt{3}-4i=-2\sqrt{3}-3i$.
Một số tính chất của phép cộng số phức
þ Tính chất kết hợp: $\left( {{z}_{1}}+{{z}_{2}} \right)+{{z}_{3}}={{z}_{1}}+\left( {{z}_{2}}+{{z}_{3}} \right),\forall {{z}_{1}};{{z}_{2}};{{z}_{3}}\in \mathbb{C}$.
þ Tính chất giao hoán: $z+z’=z’+z,\forall z’,z\in \mathbb{C}$
þ Cộng với 0: $z+0=0+z=z,\forall z\in \mathbb{C}$.
þ Với mỗi số phức $z=a+bi\text{ }\left( a;b\in \mathbb{R} \right)$ nếu kí hiệu số phức $-a-bi$là $-z$ thì ta có:
$z+\left( -z \right)=\left( -z \right)+z=0$
Số $-z$ được gọi là số đối của số phức $z$.
b) Phép trừ hai số phức
Hiệu của hai số phức $z$ và ${z}’$ là tổng của $z$ và $-z’$, tức là $z-{z}’=z+\left( -{z}’ \right)$
Nếu $z=a+bi;\text{ }{z}’={a}’+{b}’i$ thì $z-{z}’=a-{a}’+\left( b-{b}’ \right)i$.
Bài tập: $\left( 4+5i \right)-\left( 1+2i \right)=\left( 4-1 \right)+\left( 5-2 \right)i=3+3i$.
c) Phép nhân hai số phức
Tích của hai số phức $z=a+bi$ và ${z}’={a}’+{b}’i\text{ }\left( a;{a}’;b;{b}’\in \mathbb{R} \right)$ là số phức:
$z{z}’=\left( a+bi \right)\left( {a}’+{b}’i \right)=a{a}’+\left( a{b}’+{b}’a \right)i+b{b}'{{i}^{2}}=\left( a{a}’-b{b}’ \right)+\left( a{b}’+{a}’b \right)i$.
Biến đổi tương tự như trên ta có:
· ${{z}^{2}}={{\left( a+bi \right)}^{2}}={{a}^{2}}+2abi+{{\left( bi \right)}^{2}}={{a}^{2}}-{{b}^{2}}+2abi$
· ${{z}^{3}}={{\left( a+bi \right)}^{3}}={{a}^{3}}+3{{a}^{2}}bi+3a{{\left( bi \right)}^{2}}+{{\left( bi \right)}^{3}}={{a}^{3}}-3a{{b}^{2}}+\left( 3{{a}^{2}}b-{{b}^{3}} \right)i$.
· ${{\left( 1+i \right)}^{2}}=2i;\text{ }{{\left( 1-i \right)}^{2}}=-2i$.
Bài tập: $\left( 3-i \right)\left( 1+2i \right)=3+2-i+6i=5+5i$.
Một số tính chất của phép nhân hai số phức:
þ Tính chất giao hoán: $z{z}’={z}’z,\forall z;{z}’\in \mathbb{C}$.
þ Tính chất kết hợp: $\left( {{z}_{1}}{{z}_{2}} \right){{z}_{3}}={{z}_{1}}\left( {{z}_{2}}{{z}_{3}} \right),\forall {{z}_{1}};{{z}_{2}};z{{ {} }_{3}}\in \mathbb{C}$.
þ Nhân với 1: $1.z=z.1,\forall z\in \mathbb{C}$.
þ Tính chất phân phối của phép nhân đối với phép cộng: $z\left( {{z}_{1}}+{{z}_{2}} \right)=z{{z}_{1}}+z{{z}_{2}},\forall z;{{z}_{1}};{{z}_{2}}\in \mathbb{C}$.
4) Số phức liên hợp và môđun của số phức
a) Số phức liên hợp
· Số phức liên hợp của $z=a+bi\text{ }\left( a;b\in \mathbb{R} \right)$ là $a-bi$ và được kí hiệu là $\overline{z}$.
Như vậy $\overline{z}=\overline{a+bi}=a-bi$.
Bài tập: $\overline{2+5i}=2-5i$.
$\overline{4-\sqrt{3}i}=4+\sqrt{3}i$.
$\overline{i}=-i$.
$\overline{-2i}=2i$.
$\overline{5}=5$.
· Chú ý: Vì $\overline{\overline{z}}=z$ nên $\overline{\overline{z}}$ và $\overline{z}$ là hai số phức liên hợp với nhau.
· Tính chất: Với mọi số phức $z;{z}’$ ta có: $\overline{z+{z}’}=\overline{z}+\overline{{{z}’}}$ và $\overline{z{z}’}=\overline{z}.\overline{{{z}’}}$
b) Mô-đun của số phức
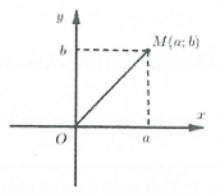Mô-đun của số phức $z=a+bi\text{ }\left( a;b\in \mathbb{R} \right)$ là số thực không âm $\sqrt{{{a}^{2}}+{{b}^{2}}}$ và được kí hiệu là $\left| z \right|$.
Trong mặt phẳng tọa độ Oxy điểm $M\left( a;b \right)$ biểu diễn số phức z.
Khi đó $OM=\sqrt{{{a}^{2}}+{{b}^{2}}}=\left| z \right|$.
Như vậy, nếu $z=a+bi\text{ }\left( a;b\in \mathbb{R} \right)$ thì $\left| z \right|=\sqrt{z.\overline{z}}=\sqrt{{{a}^{2}}+{{b}^{2}}}$.
Bài tập: $\left| -5i \right|=5;\left| 4+3i \right|=\sqrt{{{4}^{2}}+{{3}^{2}}}=5$.
5) Phép chia cho số phức khác 0
Định nghĩa: Số nghịch đảo của số phức z khác 0 là số ${{z}^{-1}}=\frac{1}{z}=\frac{\overline{z}}{z.\overline{z}}=\frac{\overline{z}}{{{\left| z \right|}^{2}}}$
Thương $\frac{{{z}’}}{z}$ của phép chia số phức ${z}’$ cho số phức z khác 0 là tích của ${z}’$ với số nghịch đảo của số phức z, tức là $\frac{{{z}’}}{z}={z}’.{{z}^{-1}}$. Như vậy, nếu $z\ne 0$ thì $\frac{{{z}’}}{z}=\frac{{z}’.\overline{z}}{{{\left| z \right|}^{2}}}$.
Bài tập: $\frac{4+i}{2-3i}=\frac{\left( 4+i \right)\left( 2+3i \right)}{\left( 2-3i \right)\left( 2+3i \right)}=\frac{5+14i}{13}$.
6) Một số các kết quả quan trọng
Cho ${{z}_{1}}={{a}_{1}}+{{b}_{1}}i;\text{ }{{z}_{2}}={{a}_{2}}+{{b}_{2}}i$ ta có:
a) $\left| {{z}_{1}}{{z}_{2}} \right|=\left| {{z}_{1}} \right|\left| {{z}_{2}} \right|$.
b)$\left| \frac{{{z}_{1}}}{{{z}_{2}}} \right|=\frac{\left| {{z}_{1}} \right|}{\left| {{z}_{2}} \right|}\,\,\left( {{z}_{2}}\ne 0 \right)$.
Chứng minh: Ta có: ${{z}_{1}}{{z}_{2}}=\left( {{a}_{1}}{{a}_{2}}-{{b}_{1}}{{b}_{2}} \right)+\left( {{a}_{1}}{{b}_{2}}+{{a}_{2}}{{b}_{1}} \right)i$
Khi đó $\left| {{z}_{1}}{{z}_{2}} \right|=\sqrt{{{\left( {{a}_{1}}{{a}_{2}}-{{b}_{1}}{{b}_{2}} \right)}^{2}}+{{\left( {{a}_{1}}{{b}_{2}}+{{a}_{2}}{{b}_{1}} \right)}^{2}}}=\sqrt{{{\left( {{a}_{1}}{{a}_{2}} \right)}^{2}}+{{\left( {{b}_{1}}{{b}_{2}} \right)}^{2}}+{{\left( {{a}_{1}}{{b}_{2}} \right)}^{2}}+{{\left( {{a}_{2}}{{b}_{1}} \right)}^{2}}}$
$=\sqrt{\left( a_{1}^{2}+b_{1}^{2} \right)\left( a_{2}^{2}+b_{2}^{2} \right)}=\left| {{z}_{1}} \right|\left| {{z}_{2}} \right|$ (đpcm)
Tổng quát: $\left| {{z}_{1}}{{z}_{2}}………{{z}_{n}} \right|=\left| {{z}_{1}} \right|\left| {{z}_{2}} \right|………\left| {{z}_{n}} \right|$
Hoàn toàn tương tự ta có thể chứng minh $\left| \frac{{{z}_{1}}}{{{z}_{2}}} \right|=\frac{\left| {{z}_{1}} \right|}{\left| {{z}_{2}} \right|}\left( {{z}_{2}}\ne 0 \right)$.
