So sánh các giá trị của hàm số – Bài toán ứng dụng của tích phân
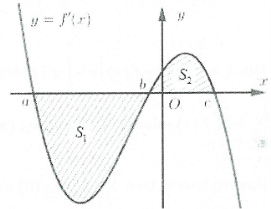
| Ví dụ 1: Cho hàm số $y=f\left( x \right)$ có đồ thị hàm số $y={f}’\left( x \right)$ cắt trục $Ox$ tại ba điểm có hoành độ $a,\,\,b,\,\,c$ thỏa mãn $a<b<c$ như hình vẽ. Mệnh đề nào sau đây đúng?
A. $f\left( a \right)>f\left( b \right)>f\left( c \right).$ B. $f\left( a \right)>f\left( c \right)>f\left( b \right).$ C. $f\left( c \right)>f\left( b \right)>f\left( a \right).$ D. $f\left( c \right)>f\left( a \right)>f\left( b \right).$ |
Lời giải:
Dựa vào đồ thị hàm số $y={f}’\left( x \right)$ ta có BBT của hàm số $y=f\left( x \right)$ như sau:
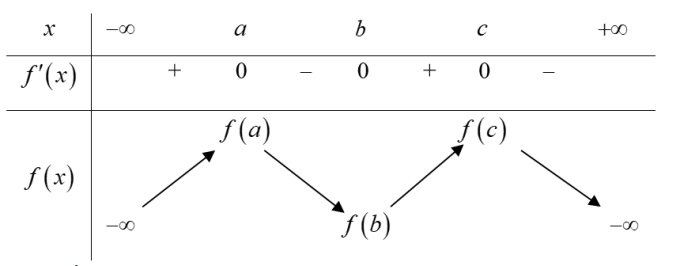 Lại có: ${{S}_{1}}=\int\limits_{a}^{b}{\left| f’\left( x \right) \right|dx=\int\limits_{a}^{b}{-f’\left( x \right)dx}}=f\left( a \right)-f\left( b \right);$ tương tự ${{S}_{2}}=f\left( c \right)-f\left( b \right)$
Lại có: ${{S}_{1}}=\int\limits_{a}^{b}{\left| f’\left( x \right) \right|dx=\int\limits_{a}^{b}{-f’\left( x \right)dx}}=f\left( a \right)-f\left( b \right);$ tương tự ${{S}_{2}}=f\left( c \right)-f\left( b \right)$
Dựa vào hình vẽ ta thấy ${{S}_{1}}>{{S}_{2}}\Rightarrow f\left( a \right)-f\left( b \right)>f\left( c \right)-f\left( b \right)\Leftrightarrow f\left( a \right)>f\left( c \right).$ Chọn B.
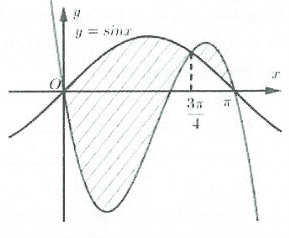
| Ví dụ 2: Cho $y=f\left( x \right)$ có đồ thị $y={f}’\left( x \right)$ như hình. Đặt $g\left( x \right)=f\left( x \right)+\cos x.$ Mệnh đề nào đúng?
A. $g\left( 0 \right)<g\left( \pi \right)<g\left( \frac{3\pi }{4} \right).$ B. $g\left( \frac{3\pi }{4} \right)<g\left( 0 \right)<g\left( \pi \right).$ C. $g\left( \pi \right)<g\left( 0 \right)<g\left( \frac{3\pi }{3} \right).$ D. $g\left( \frac{3\pi }{4} \right)<g\left( \pi \right)<g\left( 0 \right).$ |
Lời giải:
Ta có $g’\left( x \right)=f’\left( x \right)-\sin x\Rightarrow \int{g’\left( x \right)dx=\int{\left[ f’\left( x \right)-\sin x \right]dx}}$
Bảng biến thiên của hàm số $y=g\left( x \right)$
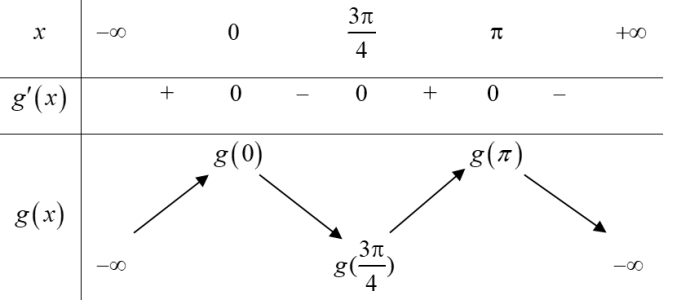 Đặt ${{S}_{1}}=\int\limits_{0}^{\frac{3\pi }{4}}{\left[ \sin x-f\left( x \right) \right]=-\int\limits_{0}^{\frac{3\pi }{4}}{g’\left( x \right)dx}}=g\left( 0 \right)-g\left( \frac{3\pi }{4} \right)$
Đặt ${{S}_{1}}=\int\limits_{0}^{\frac{3\pi }{4}}{\left[ \sin x-f\left( x \right) \right]=-\int\limits_{0}^{\frac{3\pi }{4}}{g’\left( x \right)dx}}=g\left( 0 \right)-g\left( \frac{3\pi }{4} \right)$
${{S}_{2}}=\int\limits_{\frac{3\pi }{4}}^{\pi }{\left[ f\left( x \right)-\sin x \right]=\int\limits_{\frac{3\pi }{4}}^{\pi }{g’\left( x \right)dx=g\left( \pi \right)-g\left( \frac{3\pi }{4} \right)}}$
Dựa vào hình vẽ ta có ${{S}_{1}}>{{S}_{2}}\Rightarrow g\left( 0 \right)>g\left( \pi \right).$ Do đó $g\left( \frac{3\pi }{4} \right)<g\left( \pi \right)<g\left( 0 \right).$ Chọn D.
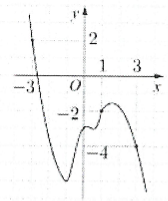
| Ví dụ 3: Cho hàm số $y=f\left( x \right)$. Đồ thị của hàm số $y={f}’\left( x \right)$ như hình bên. Đặt $g\left( x \right)=2f\left( x \right)+{{\left( x+1 \right)}^{2}}.$ Mệnh đề nào dưới đây đúng?
A. $g\left( 1 \right)<g\left( 3 \right)<g\left( -3 \right).$ B. $g\left( 1 \right)<g\left( -3 \right)<g\left( 3 \right).$ C. $g\left( 3 \right)<g\left( -3 \right)<g\left( 1 \right).$ D. $g\left( 3 \right)<g\left( -3 \right)<g\left( 1 \right).$ |
Lời giải:
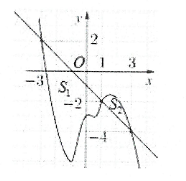
Ta có $g’\left( x \right)=2\left[ f’\left( x \right)+x+1 \right]=2\left[ f’\left( x \right)-\left( -x-1 \right) \right]$
$\Rightarrow \int{\frac{g’\left( x \right)}{2}dx=\int{\left[ f’\left( x \right)-\left( -x-1 \right) \right]dx}}$
Đường thẳng $d:y=-x-1$ đi qua các điểm $\left( -3;2 \right);\left( 1;-2 \right)$ và $\left( 3;-4 \right)$
Với $x>3$ ta có: $-x-1>f’\left( x \right)\Rightarrow g’\left( x \right)<0$
Ta có BBT của hàm số $g\left( x \right)$
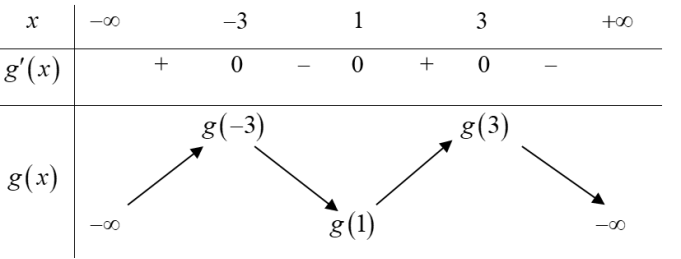
Đặt ${{S}_{1}}=\int\limits_{-3}^{1}{\left[ \left( -x-1 \right)-f’\left( x \right) \right]\text{d}}x;\,\,{{S}_{2}}=\int\limits_{1}^{3}{\left[ f’\left( x \right)-\left( -x-1 \right) \right]\text{d}x}$
Dựa vào hình vẽ ta có ${{S}_{1}}>{{S}_{2}}\Rightarrow -\int\limits_{-3}^{1}{\frac{g’\left( x \right)}{2}\text{d}x}>\int\limits_{1}^{3}{\frac{g’\left( x \right)}{2}\text{d}x}$
Do đó $g\left( -3 \right)-g\left( 1 \right)>g\left( 3 \right)-g\left( 1 \right)\Rightarrow g\left( -3 \right)>g\left( 3 \right).$ Chọn A.
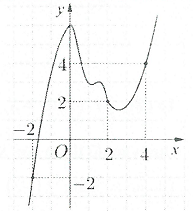
| Ví dụ 4: Cho hàm số $f\left( x \right).$ Đồ thị của hàm số $y={f}’\left( x \right)$ như hình bên. Đặt $h\left( x \right)=2f\left( x \right)-{{x}^{2}}.$ Mệnh đề nào dưới đây đúng?
A. $h\left( 4 \right)=h\left( -2 \right)>h\left( 2 \right).$ B. $h\left( 4 \right)=h\left( -2 \right)<h\left( 2 \right).$ C. $h\left( 2 \right)>h\left( -2 \right)>h\left( 4 \right).$ D. $h\left( 2 \right)>h\left( 4 \right)>h\left( -2 \right).$ |
Lời giải:
Ta có: $h’\left( x \right)=2\left[ f’\left( x \right)-x \right]\Rightarrow \int{\frac{h’\left( x \right)}{2}\text{d}x}=\int{\left[ f’\left( x \right)-x \right]\text{d}x}$
Đường thẳng \(y=x\) đi qua các điểm $\left( -2;-2 \right);\left( 2;2 \right);\left( 4;4 \right)$ trên hình vẽ
Với $x<-2$ ta có: $h’\left( x \right)<x$ suy ra hàm số nghịch biến trên khoảng $\left( -\infty ;-2 \right)$
Ta có bảng biến thiên của hàm số $h\left( x \right)$ như sau:
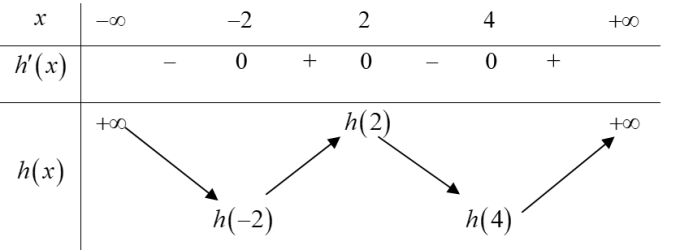
Đặt ${{S}_{1}}=\int\limits_{-2}^{2}{\left[ f’\left( x \right)-x \right]\text{d}}x;\,\,{{S}_{2}}=\int\limits_{2}^{4}{\left[ x-f’\left( x \right) \right]\text{d}x}$
Dựa vào hình vẽ ta có: ${{S}_{1}}>{{S}_{2}}\Rightarrow \int\limits_{-2}^{2}{\frac{h\left( x \right)}{2}\text{d}x}>\int\limits_{2}^{4}{\frac{-h\left( x \right)}{2}\text{d}x}$
$\Rightarrow h\left( 2 \right)-h\left( -2 \right)>h\left( 2 \right)-h\left( 4 \right)\Leftrightarrow h\left( 4 \right)>h\left( -2 \right).$ Chọn D.
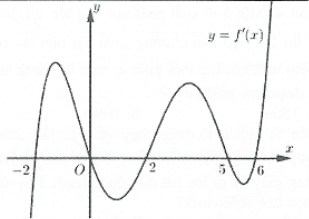
| Ví dụ 5: Cho hàm số $y=f\left( x \right).$ Đồ thị hàm số $y={f}’\left( x \right)$ như hình vẽ bên. Đặt $M=\underset{\left[ -2;6 \right]}{\mathop{\max }}\,f\left( x \right),$ $m=\underset{\left[ -2;6 \right]}{\mathop{\min }}\,f\left( x \right),$ $T=M+m.$ Mệnh đề nào dưới đây đúng?
A. $T=f\left( 0 \right)+f\left( -2 \right).$ B. $T=f\left( 5 \right)+f\left( -2 \right).$ C. $T=f\left( 5 \right)+f\left( 6 \right).$ D. $T=f\left( 0 \right)+f\left( 2 \right).$ |
Lời giải:
Dựa vào đồ thị hàm số $y=f’\left( x \right)$ ta lập được bảng biến thiên của hàm số $y=f\left( x \right)$
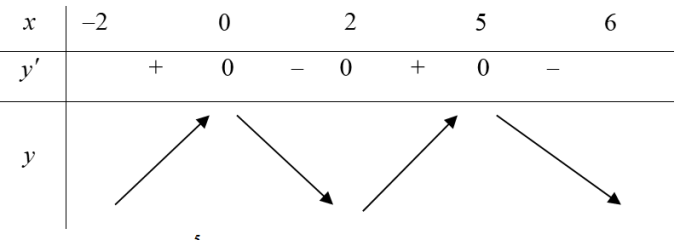
Ta đặt: $\int\limits_{2}^{0}{f’\left( x \right)\text{d}}x={{S}_{1}}=f\left( 0 \right)-f\left( 2 \right);\,\,\int\limits_{2}^{5}{f’\left( x \right)\text{d}x}={{S}_{2}}=f\left( 5 \right)-f\left( 2 \right)$
Dựa vào đồ thị ta có: ${{S}_{2}}>{{S}_{1}}\Rightarrow f\left( 5 \right)>f\left( 0 \right)\Rightarrow M=f\left( 5 \right)$ (loại A và D).
Ta cần so sánh $f\left( -2 \right)$ và $f\left( 6 \right)$
Tương tự ta có: $\int\limits_{-2}^{0}{f’\left( x \right)\text{d}}x=f\left( 0 \right)-f\left( -2 \right)={{S}_{3}};\,\,\int\limits_{6}^{5}{f’\left( x \right)\text{d}x}=f\left( 5 \right)-f\left( 6 \right)={{S}_{4}}$
Quan sát đồ thị suy ra ${{S}_{3}}>{{S}_{4}}\Rightarrow f\left( 0 \right)-f\left( -2 \right)>f\left( 5 \right)-f\left( 6 \right)\Rightarrow f\left( 6 \right)-f\left( -2 \right)=f\left( 5 \right)-f\left( 0 \right)>0$
Do đó $f\left( -2 \right)<f\left( 6 \right)\Rightarrow m=f\left( -2 \right).$ Chọn B.