Bài tập số phức bấm máy casio – Tính toán cơ bản với số phức có đáp án và cách giải
Phương pháp giải tính toán cơ bản với số phức
Phương pháp CASIO: Ngoài cách thực hiện tính toán thông thường, ta còn có thể sử dụng máy tính CASIO để hỗ trợ việc tính toán các phép tính số phức.
Bước 1: Nhấn Mode 2 để chuyển sang màn hình tính toán số phức (màn hình CMPLX).
![]()
Bước 2: Nhập biểu thức cần tính toán với số i ta bấm: ![]()
Chú ý:
1. (Tổ hợp phím SHIFT – 2 – 2 – Anpha X): Conjg là số phức liên hợp của X.
![]()
2. (Tổ hợp phím SHIFT – Abs – Anpha – X): $\left| X \right|$ là modun của số phức X

Bài tập trắc nghiệm số phức có Lời giải chi tiết
|
Bài tập 1: Tìm phần thực và phần ảo của số phức $z={{\left( 1+i \right)}^{2}}-\left( 3+i \right)$ A. Phần thực bằng 3 và phần ảo bằng i. B. Phần thực bằng -3 và phần ảo bằng 1. C. Phần thực bằng -3 và phần ảo bằng i. D. Phần thực bằng -3 và phần ảo bằng -1. |
Lời giải chi tiết
Ta có: $z={{\left( 1+i \right)}^{2}}-\left( 3+i \right)=\left( 1+2i+{{i}^{2}} \right)-3-i=2i-3-i=-3+i$.
Phần thực bằng -3 và phần ảo bằng 1. Chọn B.
|
Bài tập 2: Cho hai số phức ${{z}_{1}}=2+3i$ và ${{z}_{2}}=3-i$. Tính môđun của số phức $z={{z}_{1}}+{{z}_{2}}$ A. $\left| z \right|=3\sqrt{3}$. B. $\left| z \right|=\sqrt{30}$. C. $\left| z \right|=\sqrt{29}$. D. $\left| z \right|=5\sqrt{2}$. |
Lời giải chi tiết
Ta có: $z={{z}_{1}}+{{z}_{2}}=5+2i\Rightarrow \left| z \right|=\sqrt{29}$. Chọn C.
|
Bài tập 3: Tìm các số thực x; y biết $x-\left( y+1 \right)i=2+3i$ A. $x=2;y=2$. B. $x=2;y=-2$. C. $x=2;y=-4$. D. $x=3;y=-4$. |
Lời giải chi tiết
Do $x-\left( y+1 \right)i=2+3i\Leftrightarrow \left\{ \begin{array} {} x=2 \\ {} -\left( y+1 \right)=3 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} x=2 \\ {} y=-4 \\ \end{array} \right.$. Chọn C.
|
Bài tập 4: Cho số phức $z=2m-1+3mi\left( m\in \mathbb{R} \right)$. Tìm m biết $\left| z \right|=\sqrt{10}$ A. $m=\left\{ 1;\frac{9}{13} \right\}$. B. $m=\left\{ -1;\frac{9}{13} \right\}$. C. $m=\left\{ -1;-\frac{9}{13} \right\}$. D. $m=\left\{ 1;-\frac{9}{13} \right\}$. |
Lời giải chi tiết
Ta có: $\left| z \right|=\sqrt{10}\Leftrightarrow {{\left( 2m-1 \right)}^{2}}+{{\left( 3m \right)}^{2}}=10\Leftrightarrow 13{{m}^{2}}-4m-9=0\Leftrightarrow \left[ \begin{array} {} m=1 \\ {} m=\frac{-9}{13} \\ \end{array} \right.$. Chọn D.
|
Bài tập 5: Cho số phức z thỏa mãn: $\overline{z}={{\left( 1+\sqrt{3}i \right)}^{2}}+{{\left( 1-\sqrt{3}i \right)}^{2}}$. Tính môđun của số phức $w=iz+3$. A. $\left| w \right|=5$. B. $\left| w \right|=7$. C. $\left| w \right|=9$. D. $\left| w \right|=1$. |
Lời giải chi tiết
Ta có: $\overline{z}={{\left( 1+\sqrt{3}i \right)}^{2}}+{{\left( 1-\sqrt{3}i \right)}^{2}}=1+2i\sqrt{3}-3+1-2i\sqrt{3}-3=-4\Rightarrow z=-4$
Do đó $w=-4i+3\Rightarrow \left| w \right|=5$. Chọn A
|
A. $w=-3+2i$. B. $w=-3-2i$. C. $w=2-3i$. D. $w=2+3i$. |
Lời giải chi tiết
Điểm $M\left( -3;2 \right)\Rightarrow z=-3+2i\Rightarrow w=\overline{z}=-3-2i$. Chọn B.
|
Bài tập 7: Cho số phức z thỏa mãn $\left| z \right|=\sqrt{5}$. Tính mô-đun của số phức $w=\left( 3+4i \right)z$. A. $\left| \text{w} \right|=5\sqrt{2}$. B. $\left| \text{w} \right|=5\sqrt{5}$. C. $\left| \text{w} \right|=5$. D. $\left| \text{w} \right|=10$. |
Lời giải chi tiết
Ta có: $w=\left( 3+4i \right)z=\left| 3+4i \right|.\left| z \right|=5.\left| z \right|=5\sqrt{5}$. Chọn C.
|
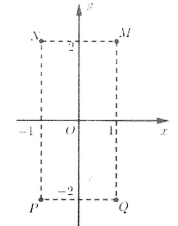
Bài tập 8: Cho số phức z thỏa mãn $\left( 1+i \right)z=3-i$. Hỏi điểm biểu diễn z là điểm nào trong các điểm M, N, P Q ở hình bên. A. Điểm P. B. Điểm Q. C. Điểm M. D. Điểm N. |
Lời giải chi tiết
Ta có: $z=\frac{3-i}{1+i}=1-2i$ Þ Điểm biểu diễn số phức z là điểm $Q\left( 1;-2 \right)$. Chọn B.
|
Bài tập 9: Cho số phức $\overline{z}=\frac{{{\left( 1-i\sqrt{3} \right)}^{3}}}{1-i}$. Tìm mô-đun của số phức $w=\overline{z}+iz$ A. $\left| w \right|=0$. B. $\left| w \right|=8\sqrt{2}$. C. $\left| w \right|=8$. D. $\left| w \right|=4\sqrt{2}$. |
Lời giải chi tiết
Ta có: $\overline{z}=\frac{{{\left( 1-i\sqrt{3} \right)}^{3}}}{1-i}=\frac{1-3i\sqrt{3}+3{{\left( i\sqrt{3} \right)}^{2}}-3{{i}^{3}}\sqrt{3}}{1-i}=\frac{-8}{1-i}=-4-4i\Rightarrow z=-4+4i$
Do đó $w=\overline{z}+iz=-4-4i+i\left( -4+4i \right)=-8-8i\Rightarrow \left| w \right|=8\sqrt{2}$. Chọn B.
|
Bài tập 10: Cho số phức z thỏa mãn điều kiện $\left( 1+i \right)\left( z-i \right)+2z=2i$. Mô-đun của số phức $w=z+1$ là A. $2\sqrt{2}$. B. 1. C. $\sqrt{2}$. D. 2. |
Lời giải chi tiết
$\text{PT}\Leftrightarrow \left( 1+i \right)z-\left( 1+i \right)i+2z=2i\Leftrightarrow z\left( 3+i \right)=3i-1\Leftrightarrow z=\frac{3i-1}{3+i}=i\Rightarrow \left| z+1 \right|=\sqrt{2}$. Chọn C.
|
Bài tập 11: Tìm phần ảo của số phức z thỏa mãn ${{\left( 1+i \right)}^{2}}\left( 2-i \right)z=8+i+\left( 1+2i \right)z$ A. 2. B. 2i. C. -3. D. -3i. |
Lời giải chi tiết
Sử dụng CASIO ta có: ${{\left( 1+i \right)}^{2}}\left( 2-i \right)=2+4i\Rightarrow \left( 2+4i \right)z-\left( 1+2i \right)z=8+i$
$\Leftrightarrow \left( 1+2i \right)z=8+i\Leftrightarrow z=\frac{8+i}{1+2i}=2-3i$
Do đó phần ảo của số phức z là -3. Chọn C.

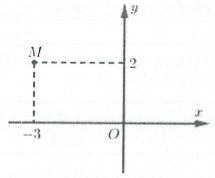 Bài tập 6: Điểm M trên hình vẽ biểu diễn số phức z. Số phức liên hợp của số phức z là:
Bài tập 6: Điểm M trên hình vẽ biểu diễn số phức z. Số phức liên hợp của số phức z là: