LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
1. Khảo sát về sự truyền tải điện năng
Giả sử ta cần truyền đi công suất điện P từ nhà máy đến nơi tiêu thụ
Ta có: $P=UI\cos \varphi .$ ($\cos \varphi $ toàn mạch)
Trong đó: U là hiệu điện thế tại nhà máy.
I là cường độ dòng điện chạy trên dây dẫn.
Khi đó: $I=\frac{P}{U\cos \varphi }.$
Dây dẫn có điện trở r, do đó công suất hao phí do tỏa nhiệt là $\Delta P={{I}^{2}}r=r\cdot \frac{{{P}^{2}}}{{{\left( U\cos \varphi \right)}^{2}}}.$
Khi đó công suất có ích là: ${P}’=P-\Delta P\Rightarrow {P}’=P-\frac{r{{P}^{2}}}{{{\left( U\cos \varphi \right)}^{2}}}.$
Hiệu suất của quá trình truyền tải điện năng: $H=\frac{{{P}’}}{P}=\frac{P-\Delta P}{P}=1-\frac{\Delta P}{P}=1-\frac{rP}{{{\left( U\cos \varphi \right)}^{2}}}.$
Độ giảm điện áp (Độ giảm thế trên đường dây):$\Delta U=I.r.$
Điện trở của dây dẫn: $r=\rho \frac{\ell }{S}$ trong đó $\rho $ là điện trở suất (đơn vị $\Omega .m$).
$\ell $ (m) là độ dài dây dẫn và là $S\left( {{m}^{2}} \right)$ tiết diện của dây dẫn.
(Chú ý: dẫn điện bằng 2 dây).
2. Cách giảm hao phí.
Ta có: $\Delta P={{I}^{2}}r=I\Delta U=r\cdot \frac{{{P}^{2}}}{{{\left( U\cos \varphi \right)}^{2}}}.$
Do P, $\cos \varphi $ xác định do đó muốn giảm hao phí ta giảm r hoặc tăng U.
Biện pháp giảm r có những hạn chế (chẳng hạn muốn giảm r phải thay dây đồng bằng dây bac, hoặc siêu dẫn… quá tốn kém). Nếu không phải tăng tiết diện dây đồng, nghĩa là tăng khối lượng dây điện nên phải tăng số lượng cột điện vì dây nặng hơn.
Do đó người ta lựa chọn phương án tăng U để giảm hao phí trên dây. 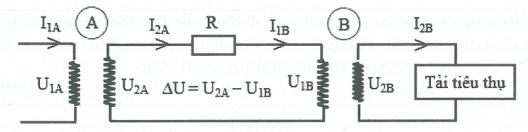
3. Sơ đồ truyền tải điện năng có sử dụng máy biến áp
– Tải tiêu thụ: ${{P}_{ta\hat{u}i}}={{U}_{ta\hat{u}i}}.{{I}_{ta\hat{u}i}}={{U}_{2B}}.{{I}_{2B}}\,\left( {{U}_{2B}}={{U}_{ta\hat{u}i}};\,{{I}_{2B}}={{I}_{ta\hat{u}i}} \right)$
– Máy hạ áp B: ${{k}_{B}}=\frac{{{U}_{1B}}}{{{U}_{2B}}}=\frac{{{N}_{1B}}}{{{N}_{2B}}}=\frac{{{I}_{1B}}}{{{I}_{2B}}}>1\Rightarrow {{U}_{1B}}\,va\,{{I}_{1B}}?$
– Trên dây:${{I}_{1B}}={{I}_{2A}};\,\Delta U={{I}_{1B}}.R={{I}_{2A}}.R={{U}_{2A}}-{{U}_{1B}}\Rightarrow {{U}_{2A}}\,va\,{{I}_{2A}}?$
– Máy tăng áp A: ${{k}_{A}}=\frac{{{U}_{1A}}}{{{U}_{2A}}}=\frac{{{I}_{1A}}}{{{I}_{2A}}}\Rightarrow {{U}_{1A}}\,va\,{{I}_{1A}}?$
