I. Phương trình lượng giác cơ bản
a) Phương trình \(\sin x = m\).
+) Nếu \(\left| m \right| > 1\) thì phương trình vô nghiệm.
+) Nếu \(\left| m \right| \le 1\) thì phương trình \( \Leftrightarrow \left[ \begin{array}{l}x = \arcsin m + k2\pi \\x = \pi – \arcsin m + k2\pi \end{array} \right.\)
Đặc biệt: \(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi – \alpha + k2\pi \end{array} \right.\left( {k \in Z} \right)\)
b) Phương trình \(\cos x = m\).
+) Nếu \(\left| m \right| > 1\) thì phương trình vô nghiệm.
+) Nếu \(\left| m \right| \le 1\) thì phương trình \( \Leftrightarrow \left[ \begin{array}{l}x = \arccos m + k2\pi \\x = – \arccos m + k2\pi \end{array} \right.\)
Đặc biệt: \(\cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = – \alpha + k2\pi \end{array} \right.\left( {k \in Z} \right)\)
c) Phương trình \(\tan x = m\).
Phương trình luôn có nghiệm \(x = \arctan m + k\pi \).
Đặc biệt: \(\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in Z} \right)\)
d) Phương trình \(\cot x = m\).
Phương trình luôn có nghiệm \(x = {\mathop{\rm arccot}\nolimits} m + k\pi \).
Đặc biệt: \(\cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in Z} \right)\)
e) Các trường hợp đặc biệt
\( + )\sin x = 0 \Leftrightarrow x = k\pi ;\) \(\cos x = 0 \Leftrightarrow x = \dfrac{\pi }{2} + k\pi \)
\( + )\sin x = – 1 \Leftrightarrow x = – \dfrac{\pi }{2} + k2\pi ;\) \(\cos x = – 1 \Leftrightarrow x = \pi + k2\pi \)
\( + )\sin x = 1 \Leftrightarrow x = \dfrac{\pi }{2} + k2\pi ;\) \(\cos x = 1 \Leftrightarrow x = k2\pi \)
II. Phương trình bậc nhất đối với một hàm số lượng giác
– Phương trình \(at + b = 0\left( {a,b \in R,a \ne 0} \right)\) với \(t = \sin x\left( {\cos x,\tan x,\cot x} \right)\) là phương trình bậc nhất đối với một hàm số lượng giác \(\sin ,\cos ,\tan ,\cot \).
– Cách giải: Biến đổi \(at + b = 0 \Leftrightarrow t = – \dfrac{b}{a}\) và giải phương trình lượng giác cơ bản.
III. Kĩ năng tổng hợp và loại nghiệm bằng đường tròn lượng giác
1. Lý thuyết
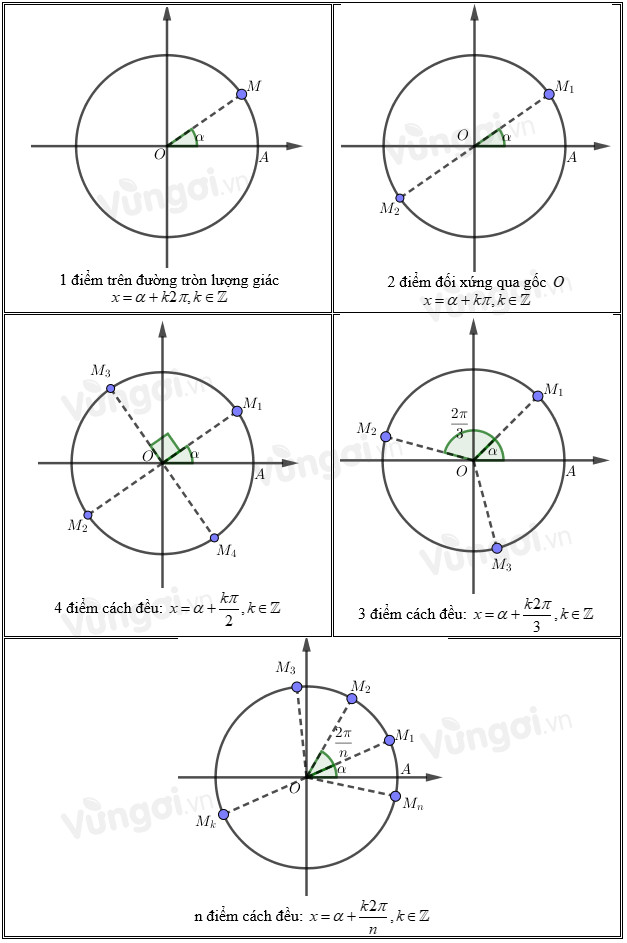
2. Ví dụ
Tìm và biểu diễn các nghiệm của phương trình sau trên đường tròn lượng giác:
a) \(\sin \left( {2x + \dfrac{\pi }{3}} \right) = \dfrac{1}{2}\)\( \Leftrightarrow \left[ \begin{array}{l}2x + \dfrac{\pi }{3} = \dfrac{\pi }{6} + k2\pi \\2x + \dfrac{\pi }{3} = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = – \dfrac{\pi }{{12}} + k\pi \\x = \dfrac{\pi }{4} + k\pi \end{array} \right.,k \in \mathbb{Z}\).
Biểu diễn nghiệm trên đường tròn đơn vị:
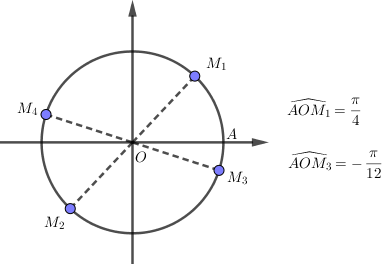
Ở đó, hai điểm \({M_1},{M_2}\) biểu diễn góc \(x = \dfrac{\pi }{4} + k\pi \) và hai điểm \({M_3},{M_4}\) biểu diễn góc \(x = – \dfrac{\pi }{{12}} + k\pi \).
b) \(\dfrac{{2\cos 2x}}{{1 – \sin 2x}} = 0\)
Điều kiện: \(1 – \sin 2x \ne 0 \Leftrightarrow \sin 2x \ne 1\) \( \Leftrightarrow 2x \ne \dfrac{\pi }{2} + k2\pi \Leftrightarrow x \ne \dfrac{\pi }{4} + k\pi \).
Phương trình \( \Leftrightarrow \cos 2x = 0 \Leftrightarrow 2x = \dfrac{\pi }{2} + k\pi \) \( \Leftrightarrow x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\).
Biểu diễn trên đường tròn đơn vị:
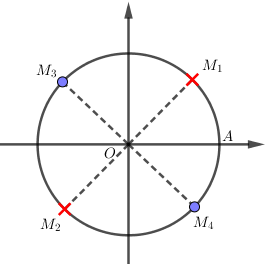
Các điểm biểu diễn \(x = \dfrac{\pi }{4} + k\pi \) là \({M_1},{M_2}\) nhưng điều kiện là \(x \ne \dfrac{\pi }{4} + k\pi \) nên hai điểm này không lấy.
Các điểm biểu diễn \(x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\) là \({M_1},{M_2},{M_3},{M_4}\) nhưng do không lấy hai điểm \({M_1},{M_2}\) nên các điểm biểu diễn nghiệm chỉ còn \({M_3},{M_4}\).
Dễ thấy hai điểm này đối xứng nhau qua \(O\) và \(\widehat {AO{M_4}} = – \dfrac{\pi }{4}\) nên nghiệm của phương trình là \(x = – \dfrac{\pi }{4} + k\pi ,k \in \mathbb{Z}\).
c) \(\dfrac{{\sqrt 3 \cot 2x – 1}}{{2\cos x + 1}} = 0\)
Điều kiện: \(2\cos x + 1 \ne 0 \Leftrightarrow \cos x \ne – \dfrac{1}{2}\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{{2\pi }}{3} + k2\pi \\x \ne – \dfrac{{2\pi }}{3} + k2\pi \end{array} \right.,k \in \mathbb{Z}\).
Khi đó phương trình \( \Leftrightarrow \sqrt 3 \cot 2x – 1 = 0 \Leftrightarrow \cot 2x = \dfrac{1}{{\sqrt 3 }}\) \( \Leftrightarrow \cot 2x = \cot \dfrac{\pi }{3} \Leftrightarrow 2x = \dfrac{\pi }{3} + k\pi \) \( \Leftrightarrow x = \dfrac{\pi }{6} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}\).
Biểu diễn trên đường tròn đơn vị:
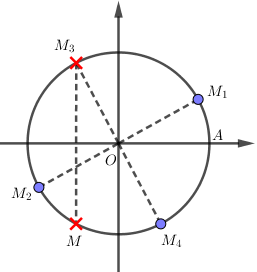
Ở đó, điểm \(M\) biểu diễn góc \(x = \dfrac{{2\pi }}{3} + k2\pi \) và điểm \({M_3}\) biểu diễn góc \(x = – \dfrac{{2\pi }}{3} + k2\pi \), ta đánh dấu đỏ thể hiện không lấy hai điểm đó (do điều kiện xác định).
Các điểm \({M_1},{M_2},{M_3},{M_4}\) là các điểm biểu diễn nghiệm \(x = \dfrac{\pi }{6} + \dfrac{{k\pi }}{2}\), trong đó không lấy điểm \({M_3}\) do điều kiện xác định.
Do đó, chỉ còn lại hai điểm \({M_1},{M_2}\) (với \(\widehat {AO{M_1}} = \dfrac{\pi }{6}\)) biểu diễn góc \(x = \dfrac{\pi }{6} + k\pi \) và điểm \({M_4}\) biểu diễn góc \(x = – \dfrac{\pi }{3} + k2\pi \) (với \(\widehat {AO{M_4}} = – \dfrac{\pi }{3}\)).
Vậy phương trình có nghiệm \(x = \dfrac{\pi }{6} + k\pi \) hoặc \(x = – \dfrac{\pi }{3} + k2\pi \) với \(k \in \mathbb{Z}\).
