I. Công thức tính diện tích hình phẳng
– Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục \(Ox\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\):
\(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
– Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\):
\(S = \int\limits_a^b {\left| {f\left( x \right) – g\left( x \right)} \right|dx} \)
II. Tính diện tích hình phẳng khi biết hai đường giới hạn
Phương pháp:
– Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục \(Ox\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\):
Công thức:
\(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
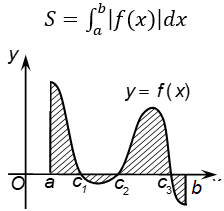
Các bước thực hiện:
+ Bước 1: Gọi \(S\) là diện tích cần xác định, ta có: \(S=\int_{a}^{b}|f(x)| d x\).
+ Bước 2: Xét dấu biểu thức \(f(x)\) trên \([a ; b]\). Từ đó phân được đoạn \([a ; b]\) thành các đoạn nhỏ, giả sử: \([a ; b]=\left[a ; c_{1}\right] \cup\left[c_{1} ; c_{2}\right] \cup \ldots \cup\left[c_{k} ; b\right]\) mà trên mỗi đoạn \(f(x)\) chỉ có một dấu.
+Bước 3: \(S=\int_{a}^{c_{1}}|f(x)| d x+\int_{c_{1}}^{c_{2}}|f(x)| d x+\ldots+\int_{c_{k}}^{b}|f(x)| d x\).
Chú ý: Nếu bài toán phát biểu dưới dạng: “Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(x=f(y)\) (liên tục trên đoạn \([a ; b]\) ) hai đường thẳng \(y=a, y=b\) và trục \(O y\)”, khi đó công thức tính diện tích là: \(S=\int_{a}^{b}|f(y)| dy \).
– Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\):
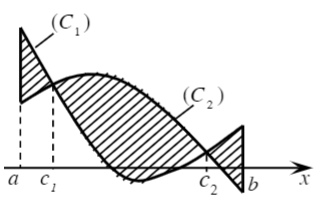
Công thức:
\(S = \int\limits_a^b {\left| {f\left( x \right) – g\left( x \right)} \right|dx} \)
Ví dụ: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = \dfrac{{x + 1}}{{x – 2}}$ và các trục tọa độ. Chọn kết quả đúng nhất.
A. $3\ln 6$
B. \(3\ln \dfrac{3}{2}\)
C. \(3\ln \dfrac{3}{2} – 2\)
D.\(3\ln \dfrac{3}{2} – 1\)
Giải:
Đồ thị hàm số cắt $Ox$ tại $\left( {-1;0} \right)$, cắt $Oy$ tại $\left( {0; – \dfrac{1}{2}} \right)$.
Hàm số $y = \dfrac{{x + 1}}{{x – 2}}$ có \(y’ = \dfrac{{ – 3}}{{{{\left( {x – 2} \right)}^2}}} < 0,\forall x \in \left( { – 1;0} \right)\) nên hàm số $y = \dfrac{{x + 1}}{{x – 2}}$ nghịch biến trên $\left( {-1;0} \right)$.
Do đó \(y < 0,\forall x \in \left( { – 1;0} \right)\)
Do đó $S = \int\limits_{ – 1}^0 {\left| {\dfrac{{x + 1}}{{x – 2}}} \right|} dx = \int\limits_{ – 1}^0 {\left( { – \dfrac{{x + 1}}{{x – 2}}} \right)} dx = – \int\limits_{ – 1}^0 {\left( {1 + \dfrac{3}{{x – 2}}} \right)} dx $
$= – \left( {x + 3\ln \left| {x – 2} \right|\mathop |\nolimits_{ – 1}^0 } \right) = – 3\ln 2 – 1 + 3\ln 3 = 3\ln \dfrac{3}{2} – 1$
Chọn D.
III. Tính diện tích hình phẳng nếu chưa biết hai đường giới hạn
Phương pháp:
– Bước 1: Giải phương trình \(f\left( x \right) = g\left( x \right)\) tìm nghiệm.
– Bước 2: Phá dấu giá trị tuyệt đối của biểu thức \(\left| {f\left( x \right) – g\left( x \right)} \right|\)
– Bước 3: Tính diện tích hình phẳng theo công thức tích phân:
\(S = \int\limits_a^b {\left| {f\left( x \right) – g\left( x \right)} \right|dx} \)
