LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
1. Các đặc điểm của sóng dừng
+) Sóng truyền trên sợi dây trong trường hợp xuất hiện các nút và các bụng gọi là sóng dừng.
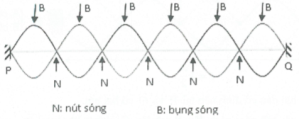
+) Sóng dừng là trường hợp đặc biệt của giao thoa sóng: đó là sự giao thoa của hai sóng kết hợp truyền ngược chiều nhau trên cùng một phương truyền sóng.
+) Bụng sóng là những điểm dao động với biên độ cực đại. Nút sóng là những điểm dao động với biên độ bằng 0 (đứng yên).
+) Mọi điểm nằm giữa 2 nút liên tiếp của sóng dừng đều dao động cùng pha và có biên độ không đổi khác nhau.
+) Mọi điểm nằm hai bên của 1 nút của sóng dừng đều dao động ngược pha.
+) Sóng dừng không có sự lan truyền năng lượng và không có sự lan truyền trạng thái dao động.
+) Khoảng cách giữa 2 nút sóng hay giữa 2 bụng sóng bất kì: ${{d}_{B\to B}}={{d}_{N\to N}}=k\frac{\lambda }{2},k=0,1,2,3,…$
+) Khoảng cách giữa 1 nút sóng với 1 bụng bất kì: ${{d}_{N\to B}}=\left( 2k+1 \right)\frac{\lambda }{4};k=0,1,2,3,…$
+) Thời gian hai lần dây duỗi thẳng liên tiếp: $\Delta t=\frac{T}{2}$
+) Bề rộng một bụng sóng là 4a.
2. Phương trình sóng tại một điểm M bất kì cách điểm phản xạ cố định O một đoạn d
Ta dễ có: ${{u}_{M}}=2a.\sin \frac{2\pi d}{\lambda }.\cos \left( \omega t-\frac{2\pi l}{\lambda } \right)$
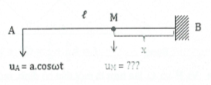
Suy ra biên độ dao động tại M: ${{A}_{M}}=2a\left| \sin \frac{2\pi d}{\lambda } \right|$
$\begin{array}{} +){{A}_{{{M}_{\max }}}}=2a\Leftrightarrow d=\left( 2k+1 \right)\frac{\lambda }{4};k\in \mathbb{Z} \\ {} +){{A}_{{{M}_{\min }}}}=0\Leftrightarrow d=k\frac{\lambda }{2};k\in \mathbb{Z} \\ \end{array}$
3. Điều kiện để có sóng dừng trên dây
a) Trường hợp sóng dừng trên một sợi dây có hai đầu cố định
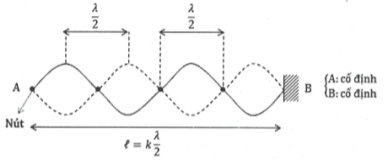
Vì P và Q là hai đầu cố định nên tại P và Q có hai nút.
Vị trí các nút: các nút nằm cách đầu P và đầu Q những khoảng bằng một số nguyên lần nửa bước sóng. Hai nút liên tiếp nằm cách nhau một khoảng bằng $\frac{\lambda }{2}$
Vị trí các bụng: xen giữa hai nút là một bụng, nằm cách đều hai nút đó. Vậy các bụng nằm cách hai đầu cố định những khoảng bằng một số lẻ lần $\frac{\lambda }{4}$ . Hai bụng liên tiếp cách nhau $\frac{\lambda }{2}$
Dây cố định hai đầu: $l=k\frac{\lambda }{2}$ với số bụng là k, số nút là k + 1
${{\lambda }_{\max }}=2l\Rightarrow {{f}_{k}}=k\frac{v}{2l}\Rightarrow {{f}_{\min }}=\frac{v}{2l}\Rightarrow {{f}_{k}}=k{{f}_{\min }}\Rightarrow {{f}_{\min }}={{f}_{k+1}}-{{f}_{k}}$
Số bó sóng k tỉ lệ với tần số f: $l=k\frac{\lambda }{2}=k\frac{v}{2f}\Rightarrow \frac{{{k}_{1}}}{{{k}_{2}}}=\frac{{{f}_{1}}}{{{f}_{2}}}$
Bước sóng dài nhất ${{\lambda }_{\max }}=2l\,khi\,k=1$ (chỉ có 1 bó sóng)
b) Trường hợp sóng dừng trên một sợi dây có một đầu cố định, một đầu tự do
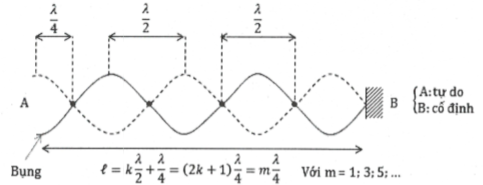
Vì P và Q lần lượt là một đầu cố định, một đầu tự do nên tại P là nút, Q là bụng.
Khoảng cách giữa hai nút liên tiếp vẫn bằng $\frac{\lambda }{2}$ . Xen giữa hai nút là một bụng. Khoảng cách giữa hai bụng liên tiếp $\frac{\lambda }{2}$
Dãy cố định hai đầu $l=\left( 2k+1 \right)\frac{\lambda }{4}$ với số bụng là k + 1, số nút là k + 1
Hoặc $l=\left( 2k-1 \right)\frac{\lambda }{4}$ với số bụng = số nút = k
${{\lambda }_{\max }}=4l\Rightarrow {{f}_{k}}=\left( 2k+1 \right)\frac{v}{2l}\Rightarrow {{f}_{\min }}=\frac{v}{2l}\Rightarrow {{f}_{k}}=\left( 2k+1 \right){{f}_{\min }}$
