BÀI TẬP SÓNG DỪNG CÓ ĐÁP ÁN CHI TIẾT
Dạng 1: Điều kiện có sóng dừng
|
Bài tập 1: Trên một sợi dây dài 2 m đang có sóng dừng với tần số 100 Hz, người ta thấy ngoài 2 đầu dây cố định còn có 3 điểm khác luôn đứng yên. Tốc độ truyền sóng trên dây là A. 100 m/s. B. 40 m/s. C. 80 m/s. D. 60 m/s. |
Lời giải chi tiết
Điều kiện sóng dừng trên dây với hai đầu cố định là $l=k\frac{\lambda }{2}$ với $sb=k,sn=k+1$
Các điểm đứng yên là các điểm nút nên tổng số nút trên dây là sn = 2 + 3 = 5 = k + l Þ k = 4
Suy ra $2=4.\frac{\lambda }{2}\Rightarrow \lambda =1m$ . Vậy tốc độ truyền sóng trên dây là $v=\lambda f=1.100=100m/s$ . Chọn A
|
Bài tập 2: Một sóng dừng có tần số 10 Hz trên sợi dây đàn hồi. Xét từ một nút thì khoảng cách từ nút đó đến bụng thứ 11 là 26,25 cm. Tốc độ truyền sóng trên dây là A. 0,5 m/s. B. 50 m/s. C. 0,4 m/s. D. 40 m/s. |
Lời giải chi tiết
Khoảng cách từ một nút đến bụng thứ n là $x=\left( 2n-1 \right)\frac{\lambda }{4}$
Với n = 11 và x = 26,25cm suy ra $26,25=\left( 2.11-1 \right)\frac{\lambda }{4}\Rightarrow \lambda =5cm$
Tốc độ truyền sóng trên dây là $v=\lambda f=5.10=50cm/s=0,5m/s.$ Chọn A
Chú ý: Khoảng cách từ nút 1 đến bụng thứ n là $x=\left( n-1 \right)\frac{\lambda }{2}$
|
Bài tập 3: Một sợi dây đàn hồi căng ngang, hai đầu cố định. Trên dây có sóng dừng, tốc độ truyền sóng không đổi. Khi tần số sóng trên dây là 42 Hz thì trên dây có 4 điểm bụng. Nếu trên dây có 6 điểm bụng thì tần số trên dây là A. 252 Hz. B. 126Hz C. 28Hz D. 63Hz |
Lời giải chi tiết
Điều kiện sóng dừng trên dây có 2 đầu cố định là $l=k.\frac{\lambda }{2}=k\frac{v}{2f}$ ,với sb = k
Với ${{f}_{1}}=42Hz\to sb=4\Rightarrow k=4$ suy ra $l=4.\frac{v}{2.42}=\frac{v}{21}\left( 1 \right)$
Với ${{f}_{1}}=mHz\to sb=6\Rightarrow k=6$ suy ra $l=6.\frac{v}{2.m}=\frac{3v}{m}\left( 2 \right)$
Lấy (1) : (2) ta được $\frac{l}{l}=\frac{v}{21}:\frac{3v}{m}\Leftrightarrow 1=\frac{m}{63}\Rightarrow m=63\Rightarrow f=63Hz.$ Chọn D
|
Bài tập 4: Một sợi dây đàn hồi dài 90 cm có một đầu cố định và một đầu tự do đang có sóng dừng. Kể cả đầu dây cố định, trên dây có 8 nút. Biết rằng khoảng thời gian giữa 6 lần liên tiếp sợi dây duỗi thẳng là 0,25 s. Tốc độ truyền sóng trên dây là A. 1,2 m/s. B. 2,9 m/s. C. 2,4 m/s. D. 2,6 m/s. |
Lời giải chi tiết
Điều kiện xảy ra sóng dừng trên dây $\Rightarrow 1=\left( 2k+1 \right)\frac{\lambda }{4}$ với số bụng = số nút = k + 1
Trên dây có 8 nút Þ k = 7 suy ra $90=\left( 2.7+1 \right)\frac{\lambda }{4}\Rightarrow \lambda =24cm$
Thời gian hai lần dây duỗi thẳng liên tiếp là $\frac{T}{2}$ suy ra $5.\frac{T}{2}=0,25\Leftrightarrow T=0,1s$
Vậy tốc độ truyền sóng là $v=\frac{\lambda }{T}=\frac{24}{0,1}=240cm/s=2,4m/s.$ Chọn C
|
Bài tập 5: Sợi dây AB dài 90 cm đầu A gắn với nguồn dao động (xem A là nút) và đầu B tự do. Quan sát thấy trên dây có 8 nút sóng dừng và khoảng thời gian 6 lần liên tiếp sợi dây duỗi thẳng là 0,25 s. Tính tốc độ truyền sóng trên dây và khoảng cách từ A đến nút thứ 7. A. 10 m/s và 0,72 m B. 2,4 m/s và 0,72 m C. 0,72 m/s và 2,4 m D. 2,4 m/s và 10 cm |
Lời giải chi tiết
Thời gian hai lần sợi dây duỗi thẳng liên tiếp là $\frac{T}{2}$ suy ra khoảng thời gian n lần tiếp sợi dây duỗi thẳng là $\Delta t=\left( n-1 \right)\frac{T}{2}$ . Với n = 6 $\to 0,25=5.\frac{T}{2}\Rightarrow T=0,1s$
Điều kiện sóng dừng trên dây với A cố định, B tự do là $l=\left( 2k-1 \right)\frac{\lambda }{4}$ với $sb=sn=k$
Với số nút bằng 8 suy ra k = 8 $\Rightarrow 90=\left( 2.8-1 \right)\frac{\lambda }{4}\Rightarrow \lambda =24cm\to v=\frac{\lambda }{T}=240cm/s$
Khoảng cách từ A ( nút thứ 1) đến nút thứ 7 là $x=\left( n-1 \right)\frac{\lambda }{2}=\left( 7-1 \right).\frac{24}{2}=72cm$ . Chọn B
|
Bài tập 6: Một thanh mảnh đàn hồi OA có đầu A tự do, đầu O được kích thích dao động theo phương vuông góc với thanh thì trên thanh có 8 bụng sóng dừng với O là nút, A là bụng. Tốc độ truyền sóng trên thanh 4 m/s và khoảng thời gian hai lần liên tiếp tốc độ dao động của A cực đại là 0,005 s. Chiều dài đoạn thẳng OA là A. 14 cm. B. 15 cm. C. 7,5 cm. D. 30 cm. |
Lời giải chi tiết
Khoảng thời gian liên tiếp tốc độ dao động của điểm A cực đại là $\frac{T}{2}\Rightarrow \frac{T}{2}=0,005\Rightarrow T=0,01s$
Điều kiện sóng dừng với O cố định, A tự do là $OA=l=\left( 2k-1 \right)\frac{\lambda }{4}$ , với sb = sn = k
Suy ra độ dài đoạn thẳng $OA=\left( 2k-1 \right)\frac{\lambda }{4}=\left( 2k-1 \right)\frac{v.T}{4}=\left( 2.8-1 \right)\frac{4.0,01}{4}=0,15m$ . Chọn B
|
Bài tập 7: Một sợi dây có chiều dài 1,5 m một đầu cố định, một đầu tự do. Kích thích cho sợi dây dao động với tần số 100 Hz thì trên dây xuất hiện sóng dừng. Tốc độ truyền sóng trên dây nằm trong khoảng từ 150 m/s đến 400 m/s. Tính bước sóng. A. 14 m. B. 2 m. C. 6 m. D. 1 cm. |
Lời giải chi tiết
Điều kiện sóng dừng một đầu cố định, một đầu tự do là $l=\left( 2k-1 \right)\frac{\lambda }{4}$ với sb = sn = k
Ta có $\lambda =\frac{v}{f}$ suy ra $l=\left( 2k-1 \right)\frac{v}{4f}\Leftrightarrow v=\frac{4l.f}{2k-1}=\frac{600}{2k-1}\in \left[ 150;400 \right]$
$\Leftrightarrow 150\le \frac{600}{2k-1}\le 400\Leftrightarrow \left\{ \begin{array}{} 2k-1\le \frac{600}{150}=4 \\ {} 2k-1\ge \frac{600}{400}=\frac{3}{2} \\ \end{array} \right.\Leftrightarrow k\in \left[ \frac{5}{4};\frac{5}{2} \right]\xrightarrow{k\in \mathbb{Z}}k=2$
Vậy bước sóng cần tính là $\lambda =\frac{4l}{2k-1}=\frac{4.1,5}{2.2-1}=2m.$ Chọn B
|
Bài tập 8: Một sợi dây AB dài 18 m có đầu dưới A dự do, đầu trên B bắn với một cần rung với tần số f có thể thay đổi được. Ban đầu trên dây có sóng dừng với đầu A bụng, B nút. Khi tần số f tăng thêm 3 Hz thì số nút trên dây tăng thêm 18 nút và A vẫn là bụng, B vẫn là nút. Tính tốc độ truyền sóng trên sợi dây. A. 1,5 m/s. B. 1,0 m/s. C. 6,0 m/s. D. 3,0 m/s. |
Lời giải chi tiết
Điều kiện sóng dừng trên dây là $l=\left( 2k-1 \right)\frac{\lambda }{4}=\left( 2k-1 \right)\frac{v}{4f}\Leftrightarrow f=\frac{\left( 2k-1 \right)v}{4l}$
Ban đầu, tần số ${{f}_{1}}=\frac{\left( 2{{k}_{1}}-1 \right)v}{4l}$ với sb = sn = k1
Khi tăng tần số f thêm 3Hz, ta được tần số ${{f}_{2}}={{f}_{1}}+3=\frac{\left( 2{{k}_{2}}-1 \right)v}{4l}$ với ${{k}_{2}}={{k}_{1}}+18$
Do đó $\frac{\left( 2{{k}_{1}}-1 \right)v}{4l}+3=\frac{\left[ 2\left( {{k}_{1}}+18 \right)-1 \right]v}{4l}\Leftrightarrow \frac{36v}{4l}=3\Leftrightarrow v=\frac{12l}{36}=6m/s.$ Chọn C
|
Bài tập 9: Một sợi dây AB dài 1 m, đầu A cố định, đầu B gắn với cần rung với tần số thay đổi được, B được coi là nút sóng. Ban đầu trên dây có sóng dừng. Khi tần số tăng thêm 20 Hz thì số nút trên dây tăng thêm 10 nút. Sau khoảng thời gian bao nhiêu sóng phản xạ từ A truyền hết một lần chiều dài sợi dây? A. 0,25 s. B. 0,5 s. C. 1,2 s. D. 1 s. |
Lời giải chi tiết
Điều kiện sóng dừng trên dây với 2 đầu cố định là $l=k\frac{\lambda }{2}$ , với sb = k; sn = k + 1
Với $\lambda =\frac{v}{f}$ suy ra $l=k.\frac{v}{2f}\Leftrightarrow f=k.\frac{v}{2l}\left( * \right)$
Vì v, l không đổi nên lấy vi phân hai vế của (*), ta được $\Delta f=\Delta k.\frac{v}{2l}\Rightarrow v=\frac{\Delta f.2l}{\Delta k}=4m/s$
Vậy thời gian sóng truyền từ A ® B là $t=\frac{AB}{v}=\frac{1}{4}=0,25s.$ Chọn A
|
Bài tập 10: Một sợi dây AB dài 100 cm căng ngang, đầu B cố định, đầu A gắn với một nhánh của âm thoa dao động điều hòa với tần số 40 Hz. Trên dây AB có một sóng dừng ổn định, A được coi là nút sóng. Tốc độ truyền sóng trên dây là 20 m/s. Kể cả A và B , trên dây có A. 3 nút và 2 bụng B. 7 nút và 6 bụng C. 9 nút và 8 bụng D. 5 nút và 4 bụng. |
Lời giải chi tiết
Chú ý: Sử dụng công thức giải nhanh với mỗi điều kiện xảy ra sóng dừng
Với A, B là 2 nút suy ra $sb=\frac{AB}{0,5\lambda }$ và $sn=sb+1$
Với A, B là 2 bụng suy ra $sn=\frac{AB}{0,5\lambda }$ và $sb=sn+1$
Với A là nút, B là bụng suy ra $sb=sn=\frac{AB}{0,5\lambda }+0,5$
Ta có $\lambda =\frac{v}{f}=\frac{20}{40}=0,5m$ . Bài toán cho A, B là 2 đầu cố định ứng với A, B là 2 nút
Suy ra số bụng $=\frac{AB}{0,5\lambda }=\frac{1}{0,5.0,5}=4\to $ số nút = số bụng + 1 = 5. Chọn D
|
Bài tập 11: Trên 1 sợi dây đàn hồi dài 20cm hai đầu A, B cố định có sóng dừng. Các điểm trên dây dao động với phương trình $u=0,5\sin \left( 0,5\pi x \right)\cos \left( 20t+\frac{\pi }{2} \right)cm$ (x đo bằng cm, t đo bằng s). Số nút sóng và bụng sóng trên đoạn dây AB (Kể cả A và B) là A. 8 bụng, 9 nút B. 9 bụng, 10 nút C. 10 bụng, 11 nút D. 8 bụng, 8 nút |
Lời giải chi tiết
Để tìm số bụng, số nút ta cần tìm được bước sóng l. Tuy nhiên bài chưa cho tần số, vận tốc mà chỉ cho phương trình sóng nên dựa vào phương trình sóng tổng quát ta tìm được l.
Phương trình dao động tổng quát là $u=a\sin \frac{2\pi x}{\lambda }\cos \left( \frac{2\pi }{T}t+\frac{\pi }{2} \right)$ suy ra $\frac{2\pi x}{\lambda }=0,5\pi x\Leftrightarrow \lambda =4cm$
Với 2 đầu A, B cố định với 2 nút suy ra $\left\{ \begin{array}{} sb=\frac{AB}{0,5\lambda } \\ {} sn=sb+1 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} sb=10 \\ {} sn=10+1=11 \\ \end{array} \right..$ Chọn C
|
Bài tập 12: Sóng dừng với hai đầu cố định, f thay đổi và l, v không đổi. Khi có tần số f trên dây có 3 bụng. Tăng tần số thêm 20 Hz thì trên dây có 5 bụng. Để trên dây có 6 bụng thì tăng f tiếp thêm một lượng bao nhiêu Hz ? A. 5 Hz. B. 15 Hz. C. 10 Hz. D. 20 Hz. |
Lời giải chi tiết
Điều kiện xảy ra sóng dừng với hai đầu cố định là $l=k\frac{\lambda }{2}=k\frac{v}{2f}$, với sb = k
Khi có tần số f, trên dây có 3 bụng $\Rightarrow k=3\Rightarrow l=\frac{3v}{2f}\left( 1 \right)$
Khi tăng tần số thêm 20 Hz, trên dây có 5 bụng Þ k = 5 Þ $l=\frac{5v}{2\left( f+20 \right)}\left( 2 \right)$
Khi tăng tần số thêm Df, trên dây có 6 bụng $\Rightarrow k=6\Rightarrow l=\frac{6v}{2\left( f+20+\Delta f \right)}\left( 3 \right)$
Từ (1) (2) (3) suy ra $\frac{3v}{2f}=\frac{5v}{2\left( f+20 \right)}=\frac{6v}{2\left( f+\Delta f+20 \right)}\Leftrightarrow \left\{ \begin{array}{} 10f=6f+120 \\ {} 6f=3f+3\Delta f+60 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} f=30 \\ {} \Delta f=10 \\ \end{array} \right.$
Vậy phải tăng tần số thêm một lượng 10 Hz để trên dây có 6 bụng sóng. Chọn C
|
Bài tập 13: Một sợi dây đàn hồi, đầu A gắn với nguồn dao động và đầu B tự do. Khi dây rung với tần số f = 12 Hz thì trên dây xuất hiện sóng dừng ổn định có 8 điểm nút trên dây với A là nút, B là bụng. Nếu đầu B được giữ cố định và tốc độ truyền sóng trên dây không đổi thì phải thay đổi tần số rung của dây một lượng nhỏ nhất bằng bao nhiêu để trên dây tiếp tục xảy ra hiện tượng sóng dừng? A. 0,5 Hz. B. 1,25 Hz. C. 0,8 Hz D. 1,6 Hz. |
Lời giải chi tiết
Khi đầu A cố định, đầu B tự do: Điều kiện xảy ra sóng dừng là $l=\left( 2k-1 \right)\frac{\lambda }{4}$ , với sn = sb = k
Vì trên dây có 8 điểm nút suy ra k = 8 và $l=\left( 2k-1 \right)\frac{v}{4f}\Leftrightarrow v=\frac{4fl}{2k-1}\left( 1 \right)$
Khi 2 đầu A, B cố định: điều kiện xảy ra sóng dừng trên dây là $l=k’\frac{\lambda ‘}{2}=k’\frac{v}{2f’}\left( 2 \right)$
Thay (1) vào (2) ta được $l=k’.\frac{\frac{4fl}{2k-1}}{2f’}\to f’=k’.\frac{2f}{2k-1}\Rightarrow f_{\min }^{‘}=\frac{2f}{2k-1}$
Và $\Delta f=\left| f’-f \right|=\left| k’.\frac{2f}{2k-1}-f \right|=f\left| \frac{2\left( k’-k \right)+1}{2k-1} \right|\to \Delta {{f}_{\min }}=\frac{f}{2k-1}=\frac{12}{2.8-1}=0,8Hz.$ Chọn C
|
Bài tập 14: Người ta tạo sóng dừng trên một sợi dây căng ngang giữa hai điểm cổ định. Sóng dừng được tạo ra trên dây lần lượt với hai tấn số gần nhau nhất 200 Hz và 300 Hz. Tần số kích thích nhỏ nhất mà vẫn tạo ra sóng dừng trên dây là A. 150 Hz. B. 100 Hz. C. 50 Hz. D. 200 Hz. |
Lời giải chi tiết
Theo điều kiện, để có sóng dừng cho 2 đầu là nút: $l=k\frac{\lambda }{2}=k.\frac{v}{2f}\Rightarrow l=\frac{k}{f}.\frac{v}{2}$
Do l, f không đổi nên buộc $\frac{n}{f}=const=$ hằng số
Khi số bó sóng k ít nhất (tức kmin = 1) thì tần số f lúc đó sẽ nhỏ nhất. Vậy ${{f}_{\min }}=\frac{v}{2l}\left( 1 \right)$
Theo bài ra, ta có 2 tần số gần giống nhau nhất là 200Hz và 300Hz, sẽ ứng với số bó sóng liên tiếp là
n và n + 1 nên ta có $\left\{ \begin{array}{} l=n.\frac{v}{2.200} \\ {} l=\left( n+1 \right).\frac{v}{2.300} \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} \frac{l}{v}=\frac{n}{400} \\ {} \frac{l}{v}=\frac{n+1}{600} \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{} \frac{n}{400}=\frac{n+1}{600} \\ {} \frac{l}{v}=\frac{n}{400} \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} n=2 \\ {} l=\frac{v}{200} \\ \end{array} \right.\left( 2 \right)$
Từ (1) và (2) ta được fmin = 100Hz. Chọn B
Chú ý: Đây là dạng bài toán đặc biệt, có 2 tần số liên tiếp mà tỉ số tần số của chúng là 2 số nguyên liên tiếp $\frac{{{f}_{1}}}{{{f}_{2}}}=\frac{200}{300}=\frac{2}{3}$ thì tần số nhỏ nhất vẫn tạo ra sóng dừng trên dây là ${{f}_{\min }}=\left| {{f}_{1}}-{{f}_{2}} \right|=100Hz$
Tương tự, nếu 2 tần số gần nhau nhất là f1, f2 có thương số $\frac{{{f}_{2}}}{{{f}_{1}}}=\frac{a}{b}$ với a, b là 2 số lẻ liên tiếp thì tần số nhỏ nhất vẫn tạo ra sóng dừng trên dây là ${{f}_{\min }}=\frac{\left| {{f}_{1}}-{{f}_{2}} \right|}{2}$
|
Bài tập 15: Một sợi dây đàn hồi một đầu cố định, một đầu tự do. Tần số dao động bé nhất để đợi dây có sóng dừng là f0. Nếu tăng chiều dài sợi dây thêm 1 m thì tần số dao động nhỏ nhất để sợi dây có sóng dừng là 5 Hz. Nếu giảm chiều dài sợi dây thêm 1 m thì tần số dao động nhỏ nhất để sợi dây có sóng dừng là 20 Hz. Giá trị của f0 là A. 14 Hz. B. 7 Hz. C. 16 Hz. D. 8 Hz |
Lời giải chi tiết
Điều kiện xảy ra sóng dừng với một đầu tự do, một đầu cố định là ${{f}_{\min }}=\frac{v}{4l}$
Khi tăng chiều dài sợi dây thêm 1m suy ra ${{f}_{1\min }}=5=\frac{v}{4\left( l+1 \right)}\left( 1 \right)$
Khi giảm chiều dài sợi dây đi thêm 1m suy ra ${{f}_{2\min }}=20=\frac{v}{4\left( l-1 \right)}\left( 2 \right)$
Từ (1) (2) suy ra $\left\{ \begin{array}{} v=20\left( l+1 \right) \\ {} v=80\left( l-1 \right) \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} v-20l=20 \\ {} v-80l=-80 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} v=\frac{160}{3} \\ {} l=\frac{5}{3} \\ \end{array} \right.\Rightarrow \frac{v}{4l}=8Hz.$ Chọn D
|
Bài tập 16: Một sợi dây thép mảnh treo thẳng đứng, đầu trên cố định, đầu dưới tự do. Dùng một nam châm điện có tần sổ 25 Hz để kích thích dao động của dây thì thấy trên dây có 9 bụng sóng, cắt dây bớt một đoạn 21 cm thì trên dây chỉ còn 6 bụng sóng. Tốc độ truyền sóng trên dây bằng A. 3,50 m/s. B. 7 m/s C. 1,75 m/s D. 10,50 m/s. |
Lời giải chi tiết
Nam châm điện có tần số 25 Hz nên tần số trên sợi dây là $f=2.25=50Hz$
Điều kiện xảy ra sóng dừng với một đầu cố định, một đầu tự do $l=\left( 2k-1 \right)\frac{\lambda }{4}$ , với sb = sn = k
+) Với chiều dài l, trên dây có 9 bụng sóng $\Rightarrow l=\left( 2.9-1 \right)\frac{\lambda }{4}=\frac{17\lambda }{4}\left( 1 \right)$
+) Khi cắt bớt dây đi 1 đoạn 21cm, trên dây có 6 bụng sóng $\Rightarrow l-21=\left( 2.6-1 \right)\frac{\lambda }{4}=\frac{11\lambda }{4}\left( 2 \right)$
Từ (1) (2) suy ra $\left\{ \begin{array}{} 4l=17\lambda \\ {} 4\left( l-21 \right)=11\lambda \\ \end{array} \right.\Rightarrow \lambda =14cm$
Vậy $v=\lambda .f=50.14=700cm/s=7m/s.$ Chọn B
Dạng 2: Bài toán về biên độ sóng dừng
|
Bài tập 1: Một sợi dây hai đầu cố định, người ta kích thích để trên dây có sóng dừng. Vận tốc truyền sóng trên dây v = 40 cm/s. Biết rằng trên dây có 8 điểm liên tiếp cách đều nhau dao động với biên độ bằng $4\sqrt{2}cm$(nhưng không phải là bụng sóng); ngoài ra hai điểm ngoài cùng của chúng cách nhau 1,4 m. Vận tốc cực đại của phần tử dao động trên dây bằng A. $10\pi cm/s$ B. $6\pi cm/s$ C. $8\pi cm/s$ D. $4\pi cm/s$ |
Lời giải chi tiết
+) Các điểm liên tiếp cách đều nhau dao động cùng biên độ thì hoặc là điểm bụng hoặc là điểm cách nút đoạn $\frac{\lambda }{8}$ suy ra $4\sqrt{2}=\frac{A\sqrt{2}}{2}\Rightarrow A=8cm$ (A là biên độ của bụng)
+) Khoảng cách giữa 2 điểm liên tiếp có biên độ $\frac{A\sqrt{2}}{2}$ là $\frac{\lambda }{4}$ , do đó 8 điểm liên tiếp sẽ có $7.\frac{\lambda }{4}$ nên
$7.\frac{\lambda }{4}=1,4\Rightarrow \lambda =80cm\Rightarrow f=0,5Hz\Rightarrow \omega =\pi rad/s\Rightarrow {{v}_{\max }}=\omega A=8\pi cm/s.$Chọn C
|
Bài tập 2: Một sóng dừng trên sợi dây căng ngang với hai đầu cố định, bụng sóng dao động với biên độ 2a. Người ta quan sát thấy những điểm có cùng biên độ ở gần nhau cách đều nhau 12 cm. Bước sóng và biên độ dao động của những điểm cùng biên độ nói trên là A. $48cm;a\sqrt{2}$ B. $24cm;a\sqrt{3}$ C. $24cm;a$ D. $48cm,a\sqrt{3}$ |
Lời giải chi tiết
Các điểm P, Q, H, K có cùng biên độ dao động và các đều nhau PQ = QH = HK = 12 cm
Mặt khác, theo tính chất của sóng dừng trên dây, ta có $PH=\frac{\lambda }{2}\Rightarrow \lambda =2PH=48cm$
Từ công thức tính biên độ sóng dừng $A=2a\left| \cos \left( 2\pi \frac{d}{\lambda }+\frac{\pi }{2} \right) \right|$
+) Tại nút thì biên độ bằng 0 suy ra $d=k\frac{\lambda }{2}$
+) Điểm H’ cách nút N một khoảng $NH’=\frac{QH}{2}=\frac{\lambda }{8}$
Vậy tại H’ có $d=k\frac{\lambda }{2}+\frac{\lambda }{8},$ thay giá trị này vào biểu thức tính biên độ ta được
$A=2a\left| \cos \left( 2\pi \left[ \left( k\frac{\lambda }{2}+\frac{\lambda }{8} \right):\lambda \right]+\frac{\pi }{2} \right) \right|=2a\left| \cos \left( k\pi +\frac{3\pi }{4} \right) \right|=2a.\frac{\sqrt{2}}{2}=a\sqrt{2}.$ Chọn A
|
Bài tập 3: M, N, P là ba điểm liên tiếp trên một sợi dây mang sóng dừng có cùng biên độ 4 cm, dao động tại N cùng pha với dao động tại M. Biết MN = 2NP = 20 cm và tần số góc của sóng là 10 rad/s. Tính tốc độ dao động tại điểm bụng khi sợi dây có dạng một đoạn thẳng. A. 40 m/s. B. 60 m/s. C. 80 cm/s. D. 120 m/s. |
Lời giải chi tiết
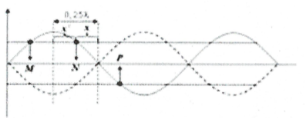
Nhận xét: Điểm bụng là điểm dao động với tốc độ cực đại nên để tìm tốc độ dao động của bụng ta tìm biên độ bụng. Cụ thể:
• Gọi x là khoảng cách từ N đến nút gần nhất và
x’ là khoảng cách từ đến điểm bụng gần nhất.
• Ta có $x+x’=0,25\lambda \Leftrightarrow \frac{MN}{2}+\frac{NP}{2}=0,25\lambda =15\Leftrightarrow \lambda =60cm$
• Biên độ dao động của điểm bụng là ${{A}_{N}}={{A}_{\max }}\left| \sin \left( \frac{2\pi x}{\lambda } \right) \right|\Rightarrow 4={{A}_{\max }}\sin \frac{2\pi .5}{60}\Rightarrow {{A}_{\max }}=8$
Vậy tốc độ của điểm bụng là ${{v}_{\max }}=\omega {{A}_{\max }}=80cm/s.$ Chọn C
Lưu ý: Có thể tính biên độ của điểm bụng bằng cách chọn x’ với ${{A}_{N}}={{A}_{\max }}\left| \cos \left( \frac{2\pi x’}{\lambda } \right) \right|$
|
Bài tập 4: Trên một sợi dây đàn hồi dài 25 cm đang có sóng dừng, người ta thấy có 6 điểm nút kể cả hai đầu A và B. Hỏi có bao nhiêu điểm trên dây dao động cùng biên độ, cùng pha với M và cách A 1 cm? A. 10 điểm. B. 9 điểm. C. 6 điểm. D. 5 điểm. |
Lời giải chi tiết
Điều kiện xảy ra sóng dừng là $l=k\frac{\lambda }{2}\to 25=5.\frac{\lambda }{2}\Leftrightarrow \lambda =
