LÝ THUYẾT TRỌNG TÂM
1. Khái niệm.
Phóng xạ là hiện tượng hạt nhân không bền tự động phóng ra các tia phóng xạ (các hạt + sóng điện từ) và biến thành hạt nhân khác. Bài tập: ${}_{92}^{235}U\to \alpha +_{90}^{231}Th$
Người ta quy ước, gọi hạt nhân phóng xạ là hạt nhân mẹ và hạt nhân sản phẩm phân rã là hạt nhân con.
2. Đặc điểm.
+) Phóng xạ có bản chất là một phản ứng hạt nhân.
+) Quá trình phân rã phóng xạ chỉ do các nguyên nhân bên trong gây ra và hoàn toàn không chịu tác động của các yếu tố thuộc môi trường ngoài như nhiệt độ áp suất,…
+) Là quá trình tự phát, ngẫu nhiên và không điều khiển được.
3. Các tia phóng xạ.
Có 3 loại tia phóng xạ: $\alpha ,\beta ,\gamma $ không nhìn thấy được nhưng có những đặc điểm mà giúp ta có thể phát hiện ra, như kích thích một số phản ứng hóa học, ion hóa không khí, làm đen kính ảnh,…
a) Tia anpha (α).
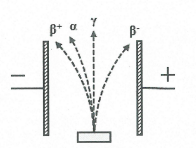
– Tia $\alpha $có bản chất là chùm hạt nhân ${}_{2}^{4}He$ mang điện tích dương nên bị lệch về phía bản tụ âm khi bay vào điện trường giữa hai bản của tụ điện.
Phương trình phóng xạ: ${}_{Z}^{A}X\xrightarrow{{}}\,{}_{Z-2}^{A-4}\,Y+{}_{2}^{4}\,\alpha $
So với hạt nhân mẹ, hạt nhân con lùi 2 ô trong bảng HTTH và có số khối nhỏ hơn 4 đơn vị.
– Các tính chất tia $\alpha $:
+) Phóng ra với vận tốc khoảng ${{2.10}^{7}}{m}/{s}\;,$ làm ion hóa môi trường và mất dần năng lượng.
+) Khả năng đâm xuyên yếu, đi được chừng vài cm trong không khí, không xuyên qua được tấm thủy tinh mỏng.
b) Tia bêta (β).
– Tia $\beta $ gồm 2 loại:
+) Tia ${{\beta }^{-}}$ có bản chất là chùm êlectrôn $\left( _{-1}^{0}e \right)$ mang điện tích âm nên lệch về phía bản tụ dương khi bay trong điện trường giữa hai bản tụ.
Phương trình phóng xạ ${{\beta }^{-}}:\,\,_{Z}^{A}X\to _{Z+1}^{A}Y+_{-1}^{0}e+_{0}^{0}\overline{v}$
$\overline{v}$ là phản nơtrinô, không mang điện, có số khối A = 0, chuyển động với vận tốc ánh sáng.
So với hạt nhân mẹ X, hạt nhân con Y tiến 1 ô trong bảng HTTH và có cùng số khối.
+) Tia ${{\beta }^{+}}$có bản chất là chùm hạt có khối lượng như electrôn nhưng mang điện tích (+e), gọi là các pôzitrôn $\left( _{1}^{0}e \right)$ và lệch về phía bản tụ âm khi bay vào trong điện trường giữa hai bản tụ điện.
Phương trình phóng xạ ${{\beta }^{+}}:\,\,_{Z}^{A}X\to _{Z-1}^{A}Y+_{1}^{0}e+_{0}^{0}\overline{v}$
So với hạt nhân mẹ X, hạt nhân con Y lùi 1 ô trong bảng HTTH và có cùng số khối.
– Các tính chất của tia $\beta $:
+) Phóng ra với vận tốc gần bằng vận tốc ánh sáng.
+) Làm ion hóa môi trường nhưng yếu hơn tia $\alpha $.
+) Khả năng đâm xuyên mạnh hơn tia $\alpha $, đi được vài mét trong không khí và vài mm trong kim loại.
c) Tia gamma (γ).
– Tia $\gamma $ có bản chất sóng điện từ có bước sóng rất ngắn.
Phóng xạ $\gamma $ không có sự biến đổi hạt nhân, chỉ có sự chuyển trạng thái và phát bức xạ: $hf={{E}_{2}}-{{E}_{1}}.$
– Các tính chất của tia $\gamma :$
+) Mang năng lượng lớn.
+) Có khả năng đâm xuyên rất mạnh, có thể đi qua lớp chì hàng chục cm, gây nguy hiểm đối với cơ thể con người.
+) Bức xạ $\gamma $ luôn đi kèm theo sau sự phóng xạ $\alpha $ hoặc $\beta .$
4. Định luật phóng xạ.
a) Chu kỳ bán rã (T).
Mỗi mẫu chất phóng xạ được đặc trưng bởi một thời gian T gọi là chu kỳ bán rã, là khoảng thời gian mà một nửa lượng chất phóng xạ bị phân rã thành hạt nhân nguyên tử khác.
b) Định luật phóng xạ.
– Xét một mẫu phóng xạ.
+) ${{N}_{o}}$ là số hạt nhân ban đầu của mẫu.
+) N là số hạt nhân còn lại sau thời gian t là: $N={{N}_{o}}{{.2}^{\frac{-t}{T}}}={{N}_{o}}.{{e}^{-\lambda t}}.$
Với $\lambda =\frac{\ln 2}{T}\left( {{s}^{-1}} \right)$ gọi là hằng số phóng xạ, đặc trưng cho từng chất phóng xạ.
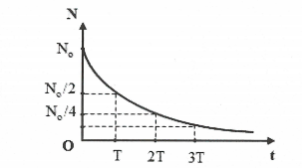
Số hạt nhân phóng xạ giảm theo quy luật hàm số mũ
c) Hoạt độ phóng xạ (H).
– Là đại lượng đặc trưng cho tính phóng xạ mạnh hay yếu của một lượng chất phóng xạ, được đo bằng số phân rã trong 1 giây. Kí hiệu: H, đơn vị Becơren (Bq) hoặc Curi (Ci)
1 giây rã/giây = 1 Bq; $1Ci=3,{{7.10}^{10}}Bq.$
– Độ phóng xạ H giảm theo thời gian với quy luật: ${{H}_{\left( t \right)}}=-\frac{\Delta N}{\Delta t}=\lambda .{{N}_{o}}.{{e}^{-\lambda t}}=\lambda {{N}_{\left( t \right)}}$
$\Rightarrow \left\{ \begin{array}{} {{H}_{o}}=\lambda {{N}_{o}} \\ {} {{H}_{\left( t \right)}}=\lambda {{N}_{\left( t \right)}} \\ \end{array} \right.$$\Rightarrow {{H}_{\left( t \right)}}={{H}_{o}}{{.2}^{-\frac{t}{T}}}={{H}_{o}}.{{e}^{-\lambda t}},$ với ${{H}_{o}}$ là độ phóng xạ ban đầu.
