LÝ THUYẾT TRỌNG TÂM, PHƯƠNG PHÁP GIẢI VÀ BÀI TẬP MÁY PHÁT ĐIỆN XOAY CHIỀU 1 PHA
Vấn đề 1. Nguyên tắc tạo ra dòng điện xoay chiều
Tổng quát
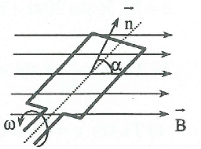
Ta cho một cuộn dây dẫn dẹt hình tròn, giả sử hai đầu dây khép kín, quay xung quanh một trục cố định nằm trong cùng mặt phẳng với cuộn dây đặt trong một từ trường đều $\overrightarrow{\operatorname{B}}$ có phương vuông góc với trục quay. Khi đó trong cuộn dây sẽ xuất hiện một dòng điện xoay chiều. Trên hình bên $\alpha $là góc giữa vecto pháp tuyến $\overrightarrow{n}$ của mặt phẳng chứa cuộn dây và vecto cảm ứng từ $\overrightarrow{\operatorname{B}}$. Giả sử lúc $\operatorname{t}=0,\text{ }\alpha =0$ đến lúc $\operatorname{t}>0,\text{ }\alpha =\omega \operatorname{t}$ với $\omega $là tốc độ góc của cuộn dây quay xung quanh trục $\Delta .$
Lúc t, từ thông qua cuộn dây là: $\Phi =\operatorname{NBS}\cos \alpha =\operatorname{NBS}\cos \omega \operatorname{t}.$
Với N là số vòng dây và S là diện tích mỗi vòng.
Vì từ thông $\Phi $qua cuộn dây biến thiên theo t nên trong cuộn dây xuất hiện suất điện động cảm ứng được tính theo định luật Fa-ra-đây: $\operatorname{e}=\frac{-d\Phi }{dt}=\operatorname{NBS}\omega \sin \omega \operatorname{t}$
Nếu cuộn dây khép tín có điện trở R thì cường độ dòng điện cảm ứng là: $\operatorname{i}=\frac{NBS\omega }{R}\sin \omega \operatorname{t}$
Đây là dòng điện xoay chiều với tần số góc $\omega $ và biên độ là ${{\operatorname{I}}_{0}}=\frac{NBS\omega }{R}.$
Chiều dương của i liên hệ với chiều pháp tuyến của $\overrightarrow{n}$ theo quy tắc nắm tay phải.
Phương pháp giải
Ghi nhớ: $\Phi =\operatorname{NBS}\cos \left( \omega \operatorname{t}+\varphi \right)={{\Phi }_{0}}\cos \left( \omega \operatorname{t}+\varphi \right)\left( \operatorname{Wb} \right)$
Từ thông cực địa của N vòng dây ${{\Phi }_{0}}=\operatorname{NBS}$
Suất điện động cảm ứng xuất hiện trong khung dây: $\operatorname{e}=\frac{-\operatorname{d}\Phi }{\operatorname{dt}}=\operatorname{NBS}\sin \left( \omega \operatorname{t}+\varphi \right)$
$=\operatorname{NBS}\cos \left( \omega \operatorname{t}+\varphi -\frac{\pi }{2} \right).$
Suy ra suất điện động cực đại ${{\text{E}}_{0}}=\text{NBS}\omega ={{\Phi }_{0}}\omega \Rightarrow $suất điện động hiệu dụng $\text{E}=\frac{{{\text{E}}_{0}}}{\sqrt{2}}.$
þ Chú ý: $\sin x=\cos \left( \frac{\pi }{2}-x \right)=\cos \left( x-\frac{\pi }{2} \right);\cos x=\sin \left( \frac{\pi }{2}-x \right)=\sin \left( x+\frac{\pi }{2} \right).$
þ Bài tập minh họa: Khung dây gồm $N=250$ vòng quay đều trong từ trường đều có cảm ứng từ $B={{2.10}^{-2}}\text{T}.$ Vectơ cảm ứng từ $\overrightarrow{\operatorname{B}}$vuông góc với trục quay của khung. Diện tích của mỗi vòng dây là $\operatorname{S}=400\text{ c}{{\text{m}}^{2}}.$ Biên độ của suất điện động cảm ứng trong khung là ${{\operatorname{E}}_{0}}=4\pi \left( \operatorname{V} \right)\approx 12,56\left( \operatorname{V} \right).$ Chọn gốc thời gian $\left( t=0 \right)$lúc pháp tuyến của khung song song và cùng chiều với $\overrightarrow{\operatorname{B}}$.
a) Viết biểu thức của suất điện động cảm ứng e theo t.
b) Xác định giá trị của suất điện động cảm ứng ở thời điểm $t=\frac{1}{40}\operatorname{s}.$
c) Xác định thời điểm suất điện động cảm ứng có giá trị $\operatorname{e}=\frac{{{\operatorname{E}}_{0}}}{2}=6,28\text{ V}\text{.}$
Giải
a) Tần số góc $\omega \text{=}\frac{{{\text{E}}_{0}}}{\operatorname{NBS}}=\frac{4\pi }{{{250.2.10}^{-2}}{{.400.10}^{-4}}}=20\pi \left( rad/s \right).$
Biểu thức của suất điện động cảm ứng tức thời:
$e=12,56sin20\pi t\text{ }\left( V \right)$ hay $\text{e}=12,56\sin \left( 20\pi \operatorname{t}-\frac{\pi }{2} \right)\left( \operatorname{V} \right).$
b) Tại $t=\frac{1}{40}\operatorname{s}$ thì $\operatorname{e}=12,56\sin \left( 20\pi .\frac{1}{40} \right)=12,56\operatorname{V}.$
c) Ta có: $e=\frac{{{\operatorname{E}}_{0}}}{2}=6,28\operatorname{V}\Rightarrow 6,28=12,56\sin 20\pi t\Leftrightarrow sin20\pi t=0,5=\sin \frac{\pi }{6}$
$\Leftrightarrow 20\pi \operatorname{t}=\left[ \begin{array}{} \frac{\pi }{6}+\operatorname{k}2\pi \\ {} \frac{5\pi }{6}+\operatorname{k}2\pi \\ \end{array} \right.\Rightarrow \operatorname{t}=\left[ \begin{array}{} \frac{1}{120}+\frac{\operatorname{k}}{10}\left( \operatorname{s} \right) \\ {} \frac{1}{24}+\frac{\operatorname{k}}{10}\left( \operatorname{s} \right) \\ \end{array} \right.$
VÍ DỤ MINH HỌA.
Bài tập 1: [Trích đề thi THPT QG 2017] Khi từ thông qua một khung dây dẫn có biểu thức $\Phi ={{\Phi }_{0}}\cos \left( \omega t+\frac{\pi }{2} \right)$ thì trong khung dây xuất hiện một suất điện động cảm ứng có biểu thức $\operatorname{e}={{E}_{0}}\cos \left( \omega \operatorname{t}+\varphi \right)$. Biết ${{\Phi }_{0}},\text{ }{{\text{E}}_{0}}$ và $\omega $ là các hằng số dương. Giá trị của $\varphi $là:
A.$\frac{-\pi }{2}\operatorname{rad}.$ B. $0\operatorname{rad}.$ C.$\frac{\pi }{2}\operatorname{rad}.$ D.$\pi \operatorname{rad}.$
HD giải: Ta có :$\operatorname{e}=\frac{-\operatorname{d}{{\Phi }_{0}}}{\operatorname{d}t}={{\Phi }_{0}}\omega \sin \left( \omega \operatorname{t}+\frac{\pi }{2} \right)={{\operatorname{E}}_{0}}\cos \left( \frac{\pi }{2}-\omega \operatorname{t}-\frac{\pi }{2} \right)={{\operatorname{E}}_{0}}\cos \left( \omega \operatorname{t} \right)$. Chọn B.
Bài tập 2: [Trích đề thi THPT QG 2017]. Một khung dây dẫn, phẳng, dẹt có 200 vòng, mỗi vòng có diện tích $600{{\operatorname{cm}}^{2}}.$ Khung dây quay đều quanh trục nằm trong mặt phẳng khung, trong một từ trường đều có vecto cảm ứng từ vuông góc với trục quay và có độ lớn $4,{{5.10}^{-2}}\operatorname{T}.$ Suất điện động e trong khung dây có tần số $50Hz.$ Chọn gốc thời gian lúc pháp tuyến của mặt phẳng khu cùng hướng với vecto cảm ứng từ. Biểu thức của e là:
A. $e=119,9cos100\pi t\left( \operatorname{V} \right).$ B. $e=169,6cos\left( 100\pi t-\frac{\pi }{2} \right)\left( \operatorname{V} \right).~$
C. $e=169,6cos100\pi t\left( \operatorname{V} \right).$ D. $\operatorname{e}=119,9cos\left( 100\pi t-\frac{\pi }{2} \right)\left( \operatorname{V} \right).$
HD giải: Ta có $e=\operatorname{NBS}\omega \sin \left( \omega \operatorname{t}+\varphi \right).$
Trong đó $NBS=200.4,{{5.10}^{-2}}{{.600.10}^{-4}}.100\pi =169,6,\text{ }\varphi =0.$
Do đó $e=169,6sin~100\pi t\left( \operatorname{V} \right)=169,6\cos \left( 100\pi t-\frac{\pi }{2} \right)\left( \operatorname{V} \right).$ Chọn B.
Bài tập 3: [Trích đề thi đại học năm 2008] Một khung dây dẫn hình chữ nhật có 100 vòng, diện tích mỗi vòng $600{{\operatorname{cm}}^{2}},$quay đều quanh trục đối xứng của khung với vận tốc góc 120 vòng/ phút trong một từ trường đều có cảm ứng từ bằng $0.2\operatorname{T}.$ Trục quay vuông góc với các đường cảm ứng từ. Chọn gốc thời gian lúc vectơ pháp tuyến của mặt phẳng khung dây ngược hướng với vectơ cảm ứng từ.
Biểu thức suất điện động cảm ứng trong khung là:
A. $e=48\pi sin\left( 40\pi \operatorname{t}-\frac{\pi }{2} \right)\left( \operatorname{V} \right).$ B. $e=4,8\pi sin\left( 4\pi \operatorname{t}+\pi \right)\left( \operatorname{V} \right).$
C. $e=48\pi sin\left( 40\pi \operatorname{t}+\pi \right)\left( \operatorname{V} \right).$ D. $e=48\pi sin\left( 40\pi \operatorname{t}-\frac{\pi }{2} \right)\left( \operatorname{V} \right).$
HD giải:
Tại thời điểm $t=0\Rightarrow \alpha =\pi $. Mặt khác $\omega =2$ vòng/s $=2.2\pi =4\pi \text{ rad/s}\text{.}$
Ta có: $\Phi \text{=NBScos}\left( 4\pi \text{t}+\pi \right)=100.0,2.0,06\cos \left( 4\pi \text{t}+\pi \right)=1,2\cos \left( 4\pi \operatorname{t}+\pi \right).$
Suy ra $e=\frac{-\text{d}\Phi }{\text{dt}}=4,8\sin \left( 4\pi \text{t}+\pi \right)\left( \text{V} \right).$ Chọn B.
Bài tập 4: [Trích đề thi cao đẳng năm 2008] Một khung dây dẫn phẳng dẹt hình chữ nhât có 500 vòng dây, diện tích mỗi vòng $54\text{c}{{\text{m}}^{\text{2}}}$. Khung dây quay đều quanh một trục đối xứng (thuộc mặt phẳng của khung), trong từ trường đều có vectơ cảm ứng từ vuông góc với trục quay và có độ lớn $0.2\operatorname{T}.$ Từ thông cực đại qua khung dây là:
A. $0,27\text{Wb}.$ B. $\text{1,08Wb}.$ C. $\text{0,81Wb}.$ D. $\text{0,54Wb}.$
HD giải: Từ thông cực đại qua khung dây là: ${{\Phi }_{0}}=\text{NBS}=500.0,{{2.54.10}^{-4}}=0,54\text{Wb}\text{.}$ Chọn D.
Bài tập 5: [Trích đề thi cao đẳng năm 2009] Từ thông qua một vòng dây dẫn là $\Phi ={{\Phi }_{0}}=\frac{{{2.10}^{-2}}}{\pi }\cos \left( 100\pi \text{t}+\frac{\pi }{4} \right)\left( \text{Wb} \right).$ Biểu thức của suất điện động cảm ứng xuất hiện trong vòng dây này là:
A. $e=-2\sin \left( 100\pi \text{t}+\frac{\pi }{4} \right)\left( V \right).$ B. $e=2\sin \left( 100\pi \text{t}+\frac{\pi }{4} \right)\left( V \right).$
C. $e=-2\sin \left( 100\pi \text{t} \right)\left( V \right).$ D. $e=2\pi \sin \left( 100\pi \text{t} \right)\left( V \right).$
HD giải: Suất điện động cảm ứng xuất hiện trong vòng dây là:
$\text{e}=\frac{-\text{d}\Phi }{\text{dt}}=100\pi .\frac{{{2.10}^{-2}}}{\pi }\sin \left( 100\pi \text{t}+\frac{\pi }{4} \right)=2\sin \left( 100\pi \text{t}+\frac{\pi }{4} \right)\left( V \right).$ Chọn B.
Bài tập 6: [Trích đề thi cao đẳng năm 2010] Một khung dây dẫn phẳng dẹt hình chữ nhật có 500 vòng dây, diện tích mỗi vòng là $220c{{\text{m}}^{\text{2}}}.$ Khung quay đều với tốc độ 50 vòng/giây quanh một trục đối xứng nằm trong mặt phẳng của khung dây, trong một từ trường đều có véctơ cảm ứng từ $\overrightarrow{\text{B}}$ vuông góc với trục quay và có độ lớn $\frac{\sqrt{2}}{5\pi }\text{T}.$ Suất điện động cực đại trong khung dây bằng:
A. $110\sqrt{2}\text{ V}\text{.}$ B. $220\sqrt{2}\text{ V}\text{.}$ C. $110\text{ V}\text{.}$ D. $\text{220 V}\text{.}$
HD giải: Ta có $\omega =$50 vòng/giây $=100\pi \text{ rad/s}\text{.}$ (một vòng ứng với $\text{2}\pi \text{ rad}$).
Suất điện động cực đại trong khung dây là${{\text{E}}_{0}}=\omega \text{NBS}=100\pi .500.\frac{\sqrt{2}}{5\pi }{{.220.10}^{-4}}=220\sqrt{2}\text{V}\text{.}$
Chọn B.
Bài tập 7: [Trích đề thi đại học năm 2011] Một khung dây dẫn phẳng quay đều với tốc độ góc $\omega $ quanh một trục cố định nằm trong mặt phẳng khung dây, trong một từ trường đều có vecto cảm ứng từ vuông góc với trục quay của khung. Suất điện động cảm ứng trong khung có biểu thức $\text{e}={{\text{E}}_{0}}\cos \left( \omega \text{t}+\frac{\pi }{2} \right)$. Tại thời điểm $\text{t}=0$, vectơ pháp tuyến của mặt phẳng khung dây hợp với vectơ cảm ứng từ một góc bằng:
A. $45{}^\circ .$ B. $180{}^\circ .$ C. $150{}^\circ .$ D. $90{}^\circ .$
HD giải: Ta có $\text{e}={{\text{E}}_{0}}\cos \left( \omega \text{t}+\frac{\pi }{2} \right)={{\text{E}}_{0}}\sin \left( \frac{\pi }{2}-\omega \text{t}-\frac{\pi }{2} \right)=-{{\text{E}}_{0}}\sin \omega \text{t=}{{\text{E}}_{0}}\sin \left( \omega \text{t+}\pi \right).$
Do đó tại thời điểm $\text{t}=0$, vectơ pháp tuyến của mặt phẳng khung dây hợp với vectơ cảm ứng từ một góc bằng $180{}^\circ .$ Chọn B.
Bài tập 8: [Trích đề thi đại học năm 2011] Một máy phát điện xoay chiều một pha có phần ứng gồm bốn cuộn dây giống nhau mắc nối tiếp. Suất điện động xoay chiều do máy phát sinh ra có tần số$50\text{Hz}$và giá trị hiệu dụng$100\sqrt{2}\text{ V}$.Từ thông cực đại qua mỗi vòng dây của phần ứng là $\frac{5}{\pi }\text{mWb}$. Số vòng dây trong mỗi cuộn dây của phần ứng là:
A.400 vòng B.100 vòng C. 71 vòng D. 200 vòng
HD giải: Ta có : ${{E}_{0}}={{\Phi }_{0}}.\omega .N\Rightarrow 200=\frac{{{5.10}^{-3}}}{\pi }.100\pi .N\Rightarrow \text{N}=400.$
Do có cuộn dây giống nhau nên mỗi cuộn có 100 vòng. Chọn B.
Bài tập 9: Một khung dây dẫn dẹt, quay đều quanh trục $\Delta $ nằm trong mặt phẳng khung dây, trong một từ trường đều có vec tơ cảm ứng từ vuông góc với trục quay $\Delta $. Từ thông cực đại qua diện tích dây bằng$\frac{11\sqrt{2}}{6\pi }\left( \text{Wb} \right).$ Tại thời điểm t, từ thông qua diện tích khung dây và suất điện động cảm ứng xuất hiện trong khung dây có độ lớn lần lượt là: $\Phi =\frac{11\sqrt{6}}{12\pi }\left( \text{Wb} \right)$ và $\text{e}=110\sqrt{2}\text{ V}\text{.}$ Tần số của suất điện động cảm ứng xuất hiện trong khung dây là:
A.60 Hz. B.100 Hz. C.50 Hz. D.120 Hz.
HD giải: T có: $\Phi \bot \text{e}$ nên ${{\left( \frac{\Phi }{{{\Phi }_{0}}} \right)}^{2}}+{{\left( \frac{\text{e}}{{{\text{E}}_{\text{0}}}} \right)}^{2}}=1.$
Trong đó ${{\text{E}}_{0}}={{\Phi }_{0}}\omega $ suy ra ${{\left( \frac{\Phi }{{{\Phi }_{0}}} \right)}^{2}}+{{\left( \frac{\text{e}}{{{\text{E}}_{\text{0}}}} \right)}^{2}}=1\Leftrightarrow {{\left( \frac{\sqrt{3}}{2} \right)}^{2}}+{{\left( \frac{\text{e}}{{{\text{E}}_{0}}} \right)}^{2}}=1.$
$\Rightarrow {{\text{E}}_{0}}=220\sqrt{2}\text{ V}\Rightarrow \omega \text{=}\frac{{{\text{E}}_{0}}}{{{\Phi }_{0}}}120\pi \Rightarrow \text{f}=\frac{\omega }{2\pi }=60\text{ Hz}\text{.}$ Chọn A.
Bài tập 10: [Trích đề thi đại học năm 2013] Một khung dây dẫn phẳng, dẹt, hình chữ nhật có diện tích $60\text{ c}{{\text{m}}^{2}}$ quay đều quanh một trục đối xứng (thuộc mặt phẳng của khung) trong từ trường đều có vec tơ cảm ứng từ vuông góc với trục quay và có độ lớn $0,4\text{ T}\text{.}$ Từ thông cực đại qua khung dây là:
A. $\text{2,4}\text{.1}{{\text{0}}^{-3}}\text{Wb}.$ B. $\text{1,2}\text{.1}{{\text{0}}^{-3}}\text{Wb}.$ C. $\text{4,8}\text{.1}{{\text{0}}^{-3}}\text{Wb}.$ D.$\text{0,6}\text{.1}{{\text{0}}^{-3}}\text{Wb}.$
HD giải: Từ thông cực đại qua khung dây là ${{\Phi }_{0}}=\text{NBS}=1.0,{{4.60.10}^{-4}}=2,{{4.10}^{-3}}\text{ Wb}.$ Chọn A.
Bài tập 11: Từ thông xuyên qua một khung dây dẫn phẳng biến thiên điều hòa theo thời gian theo quy luật$\Phi ={{\Phi }_{0}}\sin \left( \omega \text{t}+{{\varphi }_{1}} \right)$ làm cho khung dây xuất hiện một suất điện động cảm ứng$\text{e}={{\text{E}}_{0}}\sin \left( \omega \text{t}+{{\varphi }_{2}} \right)$. Hiệu số ${{\varphi }_{2}}-{{\varphi }_{1}}$ nhận giá trị nào?
A. $-\frac{\pi }{2}.$ B. $\frac{\pi }{2}.$ C. 0. D. $\pi .$
HD giải: Ta có $\text{e}=\frac{-\text{d}\Phi }{\text{dt}}=-\omega {{\Phi }_{0}}\cos \left( \omega \text{t}+{{\varphi }_{1}} \right)=\omega {{\Phi }_{0}}\sin \left( \omega \text{t}+{{\varphi }_{1}}-\frac{\pi }{2} \right).$
Do đó ${{\varphi }_{2}}-{{\varphi }_{1}}=\frac{-\pi }{2}.$ Chọn A.
Bài tập 12: Một khung dây dẫn phẳng có diện tích $S=100\text{ c}{{\text{m}}^{\text{2}}}$ gồm 200 vòng dây quay đều với vận tốc 2400 vòng/phút trong một từ trường đều có cảm ứng từ $\overrightarrow{\text{B}}$vuông góc trục quay của khung và có độ lớn $\text{B}=0,005\text{T}\text{.}$ Từ thông cực địa gửi qua khung là:
A. $\text{24Wb}\text{.}$ B. $\text{2,5Wb}\text{.}$ C. $\text{0,4Wb}\text{.}$ D. $\text{0,01Wb}\text{.}$
HD giải: Từ thông cực đại qua khung dây là ${{\Phi }_{0}}=\text{NBS}=200.0,{{005.100.10}^{-4}}=0,01\text{Wb}.$
Chọn D.
Bài tập 13: Một khung dây dẫn quay đều quanh trong một từ trường đều có cảm ứng từ $\overrightarrow{\text{B}}$ vuông góc trục quay của khung với vận tốc 150 vòng/phút. Từ thông cực đại gửi qua khung là $10/\pi \left( \text{W}b \right).$ Suất điện động hiệu dụng trong khung là:
A. $\text{25 V}\text{.}$ B. $\text{25}\sqrt{2}\text{ V}\text{.}$ C. $\text{50 V}\text{.}$ D. $\text{50}\sqrt{2}\text{ V}\text{.}$
HD giải: Ta có $\omega \text{=150}\text{.2}\pi \text{/60=50}\pi \text{ rad/s}\Rightarrow {{\text{E}}_{0}}={{\Phi }_{0}}\omega =\frac{10}{\pi }.5\pi =50\text{V}.$
$\Rightarrow E=\frac{{{E}_{0}}}{\sqrt{2}}=25\sqrt{2}\text{ V}\text{.}$ Chọn B.
Bài tập 15: Một khung dây dẫn có diện tích S và có N vòng dây. Cho khung quay đều với vận tốc góc $\omega $trong một từ trường đều có cảm ứng từ $\overrightarrow{\text{B}}$ vuông góc với trục quay của khung. Tại thời điểm ban đầu, pháp tuyến của khung hợp với cảm ứng từ $\overrightarrow{\text{B}}$ một góc $\pi /6$. Khi đó, suất điện động tức thời trong khung tại thời điểm t là:
A. $\text{e}=\text{NBS}\omega \cos \left( \omega \text{t}+\frac{\pi }{6} \right).$ B. $\text{e}=\text{NBS}\omega \cos \left( \omega \text{t}-\frac{\pi }{3} \right).$
C. $\text{e}=\text{NBS}\omega \sin \omega \text{t}.$ D. $\text{e}=-\text{NBS}\omega \cos \omega \text{t}.$
HD giải: Ta có $\Phi =\text{NBS}\cos \left( \omega \text{t}+\frac{\pi }{6} \right).$
Khi đó $\text{e}=\frac{-d\Phi }{dt}=\text{NBS}\omega \sin \left( \omega \text{t}+\frac{\pi }{6} \right)=\text{NBS}\omega \cos \left( \omega \text{t}-\frac{\pi }{3} \right).$ Chọn B.
Bài tập 16: Một khung dây quay đều quanh trục $\text{x{x}’}$ trong một từ trường đều có đường cảm ứng từ vuông góc với trục quay $\text{x{x}’}$. Muốn tăng biên độ suất điện động cảm ứng trong khung lên 4 lần thì chu kì quay của khung phải :
A.tăng 4 lần. B.tăng 2 lần C.giảm 4 lần D.giảm 2 lần
HD giải: Ta có ${{\text{E}}_{0}}={{\Phi }_{0}}\omega ={{\Phi }_{0}}.\frac{2\pi }{\text{T}}$ do đó muốn tăng biên độ suất điện động cảm ứng trong khung lên 4 lần thì cần giảm chu kì T 4 lần. Chọn C.
Bài tập 17: Một vòng dây phẳng có đường kính 10 cm đặt trong từ trường đều có độ lớn cảm ứng từ $B=1/\pi \left( \text{T} \right).$ Từ thông gởi qua vòng dây khi véctơ cảm ứng từ $\overrightarrow{\text{B}}$ hợp với mặt phẳng vòng dây một góc $\alpha =30{}^\circ $bằng:
A. $1,{{25.10}^{-3}}\text{Wb}\text{.}$ B. $\text{0,005 Wb}\text{.}$ C. $12,5\text{ Wb}\text{.}$ D.$\text{50 Wb}\text{.}$
HD giải: Khi vectơ cảm ứng $\overrightarrow{\text{B}}$ hợp với mặt phẳng vòng dây một góc $\alpha =30{}^\circ $ thì nó hợp với vecto pháp tuyến của mặt phẳng chứa vòng dây góc $\text{60}{}^\circ $
Ta có: $\Phi \text{=NBScos}\alpha \text{=1}\text{.}\frac{1}{\pi }\left( \pi .0,{{05}^{2}} \right).\text{cos60}{}^\circ \text{=1,25}\text{.1}{{\text{0}}^{-3}}\text{Wb}.$ Chọn A.
Bài tập 18: Một khung dây đặt trong từ trường đều $\overrightarrow{\text{B}}$ có trục quay $\Delta $ của khung vuông góc với các đường cảm ứng từ. Cho khung quay đều quanh trục $\Delta $, thì suất điện động cảm ứng xuất hiện trong khung có phương trình$\text{e}=200\sqrt{2}\cos \left( \text{100}\pi \text{t }-\frac{\pi }{6} \right)V.$ Suất điện động cảm ứng xuất hiện trong khung tại thời điểm $\text{t}=\frac{1}{100}\text{s}$ là:
A. $100\sqrt{2}\text{ }V.$ B.$-100\sqrt{2}\text{ }V.$ C.$100\sqrt{6}\text{ }V.$ D. $-100\sqrt{6}\text{ }V.$
HG giải: Tại thời điểm $\text{t}=\frac{1}{100}\text{s}$ ta có: $\text{e}=200\sqrt{2}\cos \left( \text{100}\pi \frac{1}{100}\text{ }-\frac{\pi }{6} \right)V=-100\sqrt{6}V.$ Chọn D.
Bài tập 19: [Trích đề thi Chuyên ĐH Vinh 2017] Một khung dây dẫn phẳng diện tích $\text{S=300c}{{\text{m}}^{\text{2}}}$ và có 200 vòng dây quay đều trong từ trường đều có vectơ $\overrightarrow{\text{B}}$ vuông góc với trục quay của khung, độ lớn cảm ứng từ là $\text{B=0,1T}.$ Suất điện động cảm ứng tạo ra trong khung có tần số 50 Hz. Chọn gốc thời gian lúc pháp tuyến khung cùng chiều với đường sức từ. Biểu thức suất điện động cảm ứng sinh ra trong khung có dạng:
A. $e=60\pi cos\left( 100\pi \text{t}-\frac{\pi }{2} \right)\left( \text{V} \right).$ B. $e=60\pi cos100\pi t\left( \text{V} \right).$
C. $e=60\pi \sqrt{2}cos\left( 100\pi \text{t}-\frac{\pi }{2} \right)\left( \text{V} \right).$ D. $e=60\pi \sqrt{2}cos100\pi t\left( \text{V} \right).$
HD giải: Ta có $\Phi =\text{NBS}\cos \left( 100\pi \text{t} \right)\Rightarrow \Phi =0,6\cos \left( 100\pi \text{t} \right)$
$\Rightarrow \text{e}=\,-\,\frac{d\Phi }{dt}=60\pi \sin \left( 100\pi \text{t} \right)=60\pi \cos \left( 100\pi \text{t}-\frac{\pi }{2} \right)\left( \text{V} \right).$ Chọn A.
Vấn đề 2. Máy phát điện xoay chiều 1 pha
Tổng quát
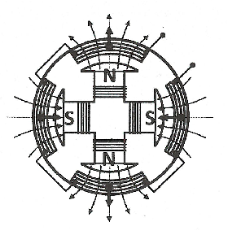
Máy phát điện xoay chiều một pha là một hệ thống biến đổi cơ năng thành điện năng, hoạt động dựa trên hiện tượng cảm ứng điện từ.
a) Cấu tạo: gồm 2 bộ phận chính:
+) Phần Cảm (tạo ra từ trường) là nam châm vĩnh cửu hoặc nam châm điện, có cấu tạo đối xứng với p cặp cực N-S.
+) Phần Ứng (tạo ra suất điện động xoay chiều) gồm 2p cuộn dây (p cặp cuộn dây) giống hệt nhau, mỗi cuộn gồm ${{N}_{0}}$ vòng dây. Các cuộn dây được bố trí cách đều nhau trên thân máy sao cho chúng đồng thời đối diện với 2p cực của nam châm.
– Phần đứng yên gọi là sta-to và phần quay gọi là rô- to $\Rightarrow $ trong máy phát điện xoay chiều một pha: phần cảm là rô- to, phần ứng là sta- to.
b) Hoạt động
Nếu máy phát có p cặp cực nam châm và roto quay với tốc độ n:
– Tần số dòng điện do máy phát ra:
$\text{f = np}$ (với n vòng/s) hoặc $\text{f =}\frac{\text{np}}{\text{60}}$ (với n vòng/phút)
– Lúc đầu pháp tuyến khung dây $\overrightarrow{\text{n}}$ hợp với cảm ứng từ góc $\overrightarrow{\text{B}}$ góc $\alpha $thì từ thông gửi qua 1 vòng dây:
${{\Phi }_{1}}=\text{BScos}\left( \text{ }\!\!\omega\!\!\text{ t+ }\!\!\alpha\!\!\text{ } \right)$
– Nếu cuộn dây có N vòng giống nhau, thì suất điện động xoay chiều trong cuộn dây là:
$\text{e}=-\text{N}\frac{\text{d}{{\Phi }_{1}}}{\text{dt}}=\omega \text{NBS}\sin \left( \text{ }\!\!\omega\!\!\text{ t+ }\!\!\alpha\!\!\text{ } \right)$
+) Từ thông cực đại gửi qua 1 vòng dây: ${{\Phi }_{0}}=\text{BS}$
+) Biên độ của suất điện động là: ${{\text{E}}_{\text{0}}}=\omega \text{NBS}$
+) Suất điện động hiệu dụng: $\text{E=}\frac{{{\text{E}}_{\text{0}}}}{\sqrt{\text{2}}}=\frac{\omega \text{NBS}}{\sqrt{2}}$
@ Chú ý:
+) Khi tần số góc $\omega $ của roto thay đổi thì ${{\text{Z}}_{\text{L}}}\text{, }{{\text{Z}}_{\text{C}}}$ thay đổi và ${{\text{E}}_{\text{0}}}={{\Phi }_{0}}\omega ={{\text{U}}_{\text{0}}}$ sẽ thay đổi
Do: $\text{f = np};\text{ }\omega \text{=2}\pi \text{f; E}=\phi \omega =\text{U}\Rightarrow \text{ n}\sim \text{f}\sim \omega \sim \text{E}\left( \text{U} \right),$ ta có: $\frac{{{\text{n}}_{\text{2}}}}{{{\text{n}}_{\text{1}}}}\text{=}\frac{{{\text{f}}_{\text{2}}}}{{{\text{f}}_{\text{1}}}}=\frac{{{\omega }_{2}}}{{{\omega }_{1}}}=\frac{{{\text{E}}_{\text{2}}}}{{{\text{E}}_{\text{1}}}}.$
+) Nếu nối 2 cực máy phát điện với mạch ngoài suy ra có dòng điện.
Khi đó $\text{I=}\frac{\text{E}}{\text{Z}}\text{.}$
Bài tập minh họa
Ví dụ 1: Một máy phát điện xoay chiều một pha có phần cảm là roto và số cặp cực là p. Khi roto quay đều với tốc độ n (vòng/phút) thì từ thông qua mỗi cuộn dây của stato biến thiên tuần hoàn với tần số (tính theo đơn vị Hz) là:
A. $\text{np/60}\text{.}$ B. $\text{n/}\left( \text{60p} \right)\text{.}$ C. $\text{60pn}\text{.}$ D. $\text{pn}\text{.}$
HD giải: Ta có: n vòng/phút = $\text{n/60 s}\text{.}$ Suy ra $\text{f =}\frac{\text{n}}{\text{60}}\text{p}\text{.}$ Chọn A.
Ví dụ 2: Một máy phát điện xoay chiều một pha có phần cảm là roto gồm 10 cặp cực ( 10 cực nam và 10 cực bắc). Roto quay với tốc độ 300 vòng/phút. Suất điện động do máy sinh ra có tần số bằng
A. $\text{3000 Hz}\text{.}$ B. $\text{50 Hz}\text{.}$ C. $\text{5 Hz}\text{.}$ D. $\text{30 Hz}\text{.}$
HD giải: 300 vòng/phút = 5 vòng/s. Do đó $\text{f = np =5}\text{.10 =50 Hz}\text{.}$ Chọn B.
Ví dụ 3: [Trích đề thi THPT QG năm 2016]. Hai máy phát điện xoay chiều một pha đang hoạt động bình thường và tạo ra hai suất điện động có cùng tần số f. Roto của máy thứ nhất có ${{\text{p}}_{\text{1}}}$cặp cực và quay với tốc độ ${{\text{n}}_{\text{1}}}\text{=1800}$ vòng/phút. Roto của máy thứ hai có ${{\text{p}}_{\text{2}}}\text{=4}$ cặp cực và quay với tốc độ ${{\text{n}}_{\text{2}}}$ . Biết ${{n}_{2}}$ có giá trị trong khoảng từ 12 vòng/giây đến 18 vòng/giây. Giá trị của f là
A. $\text{60 Hz}\text{.}$ B. $\text{50 Hz}\text{.}$ C. $\text{54 Hz}\text{.}$ D. $\text{48 Hz}\text{.}$
HD giải: Ta có: ${{\text{n}}_{\text{1}}}\text{=1800}$ vòng/phút = 30 vòng/s.
Khi đó: $\text{f = }{{\text{n}}_{\text{1}}}{{\text{p}}_{\text{1}}}\text{= }{{\text{n}}_{2}}{{\text{p}}_{2}}\Rightarrow {{\text{n}}_{2}}=\frac{{{\text{n}}_{\text{1}}}{{\text{p}}_{\text{1}}}}{{{\text{p}}_{2}}}=\frac{{{\text{p}}_{\text{1}}}\text{.30}}{\text{4}}\text{= 7,5}{{\text{p}}_{\text{1}}}\text{.}$
Do $\text{127,5}{{\text{p}}_{\text{1}}}\text{18}\Leftrightarrow \text{1,6}{{\text{p}}_{\text{1}}}\text{2,4}\Leftrightarrow {{\text{p}}_{\text{1}}}\text{=2}\Rightarrow \text{f=}{{\text{n}}_{\text{1}}}{{\text{p}}_{\text{1}}}\text{=60Hz}\text{.}$ Chọn A.
Ví dụ 4: [Trích đề thi THPT QG năm 2017]. Hai máy phát điện xoay chiều một pha A và B (có phần cảm là roto) đang hoạt động ổn định, phát ra hai suất điện động có cùng tần số 60Hz. Biết phần cảm của máy A nhiều hơn phần cảm của máy B hai cặp cực (2 cực bắc, 2 cực nam) và trong một giờ số vòng của roto hai máy chênh lệch nhau 18000 vòng. Số cặp cực của máy A và máy B lần lượt là:
A.4 và 2. B.5 và 3. C.6 và 4. D.8 và 6.
HD giải: Do hai máy phát ra suất điện động có cùng tần số nên ${{\text{n}}_{1}}{{\text{p}}_{\text{1}}}={{\text{n}}_{2}}{{\text{p}}_{2}}=60\text{ Hz}\text{.}$
Trong đó ${{\text{p}}_{\text{1}}}-{{\text{p}}_{2}}=2\xrightarrow{{{\text{p}}_{\text{1}}}>{{\text{p}}_{2}}}{{\text{n}}_{2}}>{{\text{n}}_{1}}$ và $\text{3600}{{\text{n}}_{\text{2}}}-\text{3600}{{\text{n}}_{1}}=18000\Rightarrow {{\text{n}}_{\text{2}}}-{{\text{n}}_{1}}=5.$
Suy ra ${{\text{n}}_{1}}{{\text{p}}_{\text{1}}}=\left( {{\text{n}}_{1}}+5 \right)\left( {{\text{p}}_{\text{1}}}-2 \right)=60\Leftrightarrow \left\{ \begin{array}{} {{\text{n}}_{1}}{{\text{p}}_{\text{1}}}=60 \\ {} {{\text{n}}_{1}}{{\text{p}}_{\text{1}}}+5{{\text{p}}_{\text{1}}}-2{{\text{n}}_{1}}=70 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} {{\text{n}}_{1}}{{\text{p}}_{\text{1}}}=60 \\ {} 5{{\text{p}}_{\text{1}}}-2{{\text{n}}_{1}}=10 \\ \end{array} \right.$
$\Rightarrow \frac{5{{\text{p}}_{\text{1}}}-10}{2}{{\text{p}}_{\text{1}}}=60\Rightarrow {{\text{p}}_{\text{1}}}=6\Rightarrow {{\text{p}}_{2}}=4.$ Chọn C.
Ví dụ 5: [Trích đề thi Đại Học năm 2010]. Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch AB gồm điện trở thuần R mắc nối tiếp với cuộn cảm thuần. Bỏ qua điện trở các cuộn dây của máy phát. Khi roto của máy quay đều với tốc độ n vòng/phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là 1 A. Khi roto của máy quay đều với tốc độ 3n vòng/phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là $\sqrt{3}\text{ A}\text{.}$ Nếu roto của máy quay đều với tốc độ 2n vòng/phút thì cảm kháng của đoạn mạch AB là:
A. $\text{2R}\sqrt{3}.$ B. $\frac{2\text{R}}{\sqrt{3}}.$ C. $\text{R}\sqrt{3}.$ D. $\frac{\text{R}}{\sqrt{3}}.$
HD giải: Ta có: $E\sim \omega \sim {{\text{Z}}_{\text{L}}}$
Khi tốc độ n vòng/phút thì $\omega ={{\omega }_{1}}$ và: ${{\text{Z}}_{1}}=\frac{E}{1}=E=\sqrt{{{R}^{2}}+\text{Z}_{L1}^{2}}.$
Khi tốc độ 3n vòng/phút thì $\omega =3{{\omega }_{1}}$ nên ${{\text{Z}}_{2}}=\frac{3E}{\sqrt{3}}=\sqrt{{{\text{R}}^{\text{2}}}+{{\left( 3{{\text{Z}}_{\text{L}1}} \right)}^{2}}}.$
$\Rightarrow {{\text{R}}^{\text{2}}}+9\text{Z}_{L1}^{2}=3\left( {{\text{R}}^{\text{2}}}+\text{Z}_{L1}^{2} \right)\Leftrightarrow {{\text{Z}}_{\text{L}1}}=\frac{\text{R}}{\sqrt{\text{3}}}$
Khi roto quay với tốc độ 2n vòng/phút ${{\text{Z}}_{\text{L}}}=2{{\text{Z}}_{\text{L}1}}=\frac{\text{2R}}{\sqrt{\text{3}}}.$ Chọn B.
Ví dụ 6: Nối 2 cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch AB gồm một điện trở $\text{R =30 }\!\!\Omega\!\!\text{ }$ và một tụ điện mắc nối tiếp. Bỏ qua điện trở các cuộn dây của máy phát. Khi roto của máy quay đều với tốc độ n vòng/phút thì cường độ dòng điện hiệu dụng trong mạch là 1 A. Khi roto quay đều với tốc độ 2n vòng/phút thì cường độ dòng điện hiệu dụng là $\sqrt{6}\text{ A}\text{.}$ Nếu roto quay đều với tốc độ 3n vòng/phút thì dung kháng của tụ là
A. $\text{4}\sqrt{5}\text{ }\Omega .$ B. $2\sqrt{5}\text{ }\Omega .$ C. $16\sqrt{5}\text{ }\Omega .$ D. $6\sqrt{5}\text{ }\Omega .$
HD giải: Ta có $E\sim \omega \sim \frac{1}{{{\text{Z}}_{\text{C}}}}$
Khi roto quay với tốc độ n vòng/phút thì $\omega ={{\omega }_{1}}.$
Khi đó: ${{\text{Z}}_{1}}=\sqrt{{{R}^{2}}+\text{Z}_{C1}^{2}}=\frac{E}{1}=E.$
Khi roto quay với tốc độ 2n vòng/phút thì $\omega =2{{\omega }_{1}}\Rightarrow {{Z}_{2}}=\sqrt{{{\text{R}}^{2}}+{{\left( \frac{{{\text{Z}}_{\text{C1}}}}{2} \right)}^{2}}}=\frac{\text{2E}}{\sqrt{\text{6}}}.$
Suy ra ${{\text{R}}^{2}}+\text{Z}_{C1}^{2}=\frac{6}{4}\left( {{\text{R}}^{2}}+\frac{\text{Z}_{C1}^{2}}{4} \right)\Leftrightarrow 2{{\text{R}}^{2}}+2\text{Z}_{C1}^{2}=3{{\text{R}}^{2}}+\frac{\text{3}}{4}\text{Z}_{C1}^{2}\Leftrightarrow {{\text{Z}}_{\text{C1}}}=\frac{\text{2R}}{\sqrt{\text{5}}}.$
Nếu roto quay đều với tốc độ 3n vòng/phút $\omega =3{{\omega }_{3}}\Rightarrow {{\text{Z}}_{\text{C3}}}=\frac{{{\text{Z}}_{\text{C1}}}}{3}=\frac{\text{2R}}{3\sqrt{5}}=4\sqrt{5}\text{ }\Omega .$ Chọn A.
Ví dụ 7: [Trích đề thi Đại Học năm 2013] Nối hai cực của một mát phát điện xoay chiều một pha vào hai đầu đoạn mạch A, B mắc nối tiếp gồm điện trở $\text{69,1 }\Omega \text{,}$ cuộng cảm thuần có độ tự cảm L và tụ điện có điện dung $\text{176,8 }\mu \text{F}\text{.}$ Bỏ qua điện trở thuần của các cuộn dây của máy phát. Biết roto máy phát có hai cặp cực. Khi roto quay đều với tốc độ ${{\text{n}}_{1}}=1350$ vòng/phút hoặc ${{\text{n}}_{2}}=1800$ vòng/phút thì công suất tiêu thụ của đoạn mạch AB là như nhau. Độ tự cảm L có giá trị gần giá trị nào nhất sau đây?
A. $0,8\text{ H}\text{.}$ B.$0,7\text{ H}\text{.}$ C. $0,6\text{ H}\text{.}$ D. $0,2\text{ H}\text{.}$
HD giải: Ta có: ${{\text{f}}_{1}}\text{ =}\frac{{{\text{n}}_{1}}\text{p}}{\text{60}}=45\text{Hz}\Rightarrow {{\omega }_{1}}\text{=90}\pi \text{ rad/s}\Rightarrow {{\text{Z}}_{\text{C1}}}=20\text{ }\Omega .$
Tương tự ${{\text{f}}_{2}}=60\text{ Hz, }{{\omega }_{2}}\text{=120}\pi \text{ rad/s}\Rightarrow {{\text{Z}}_{\text{C2}}}=15\text{ }\Omega .$
Do $E\sim f\xrightarrow{\text{Khi }{{\text{p}}_{1}}={{\text{p}}_{\text{2}}}\Leftrightarrow {{\text{I}}_{\text{1}}}\text{=}{{\text{I}}_{\text{2}}}}\frac{45{{\text{E}}_{\text{0}}}}{\sqrt{{{\text{R}}^{2}}+{{\left( \text{L2 }\!\!\pi\!\!\text{ }{{\text{f}}_{\text{1}}}\text{-20} \right)}^{\text{2}}}}}=\frac{\text{60}{{\text{E}}_{\text{0}}}}{\sqrt{{{\text{R}}^{2}}+{{\left( \text{L2 }\!\!\pi\!\!\text{ }{{\text{f}}_{2}}\text{-15} \right)}^{\text{2}}}}}$
$\Leftrightarrow 16\left[ {{\text{R}}^{2}}+{{\left( \text{90 }\!\!\pi\!\!\text{ L-20} \right)}^{\text{2}}} \right]=9\left[ {{\text{R}}^{2}}+{{\left( \text{120 }\!\!\pi\!\!\text{ L-15} \right)}^{\text{2}}} \right].$
Với $\text{R}=69,1\text{ }\Omega \xrightarrow{\text{SHIFT-CALC}}\text{L=0,477}\text{.}$ Chọn C.
Ví dụ 8: [Trích đề thi chuyên ĐH Vinh 2017] Nối hai đầu một máy phát điện xoay chiều một pha (bỏ qua điện trở thuần của các cuộn dây máy phát) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở R và cuộn cảm thuần. Khi roto quay với tốc độ n vòng/phút thì công suất tiêu thụ của đoạn mạch là $16\text{W}\text{.}$ Khi rôto quay với tốc độ 2n vòng/phút thì công suất tiêu thụ của đoạn mạch là $\text{20W}\text{.}$ Khi rôto quay với tốc độ 3n vòng/phút thì công suất tiêu thụ của đoạn mạch xấp xỉ
A.$17,33\text{ W}\text{.}$ B.$\text{23,42 W}\text{.}$ C.$\text{20,97 W}\text{.}$ D.$\text{21,76 W}\text{.}$
HD giải: Ta lập bảng sau:
|
Tốc độ quay của roto (vòng/phút) |
${{\text{Z}}_{\text{L}}}$ |
U |
|
n |
a |
U |
|
2n |
2a |
2U |
|
3n |
3a |
3U |
Kết hợp giả thiết ta có: $\left\{ \begin{array}{} \frac{{{\text{U}}^{\text{2}}}\text{R}}{{{\text{R}}^{\text{2}}}\text{+}{{\text{a}}^{\text{2}}}}\text{=16} \\ {} \frac{\text{4}{{\text{R}}^{\text{2}}}\text{U}}{{{\text{R}}^{\text{2}}}\text{+4}{{\text{a}}^{\text{2}}}}\text{=20} \\ \end{array} \right.\Rightarrow \frac{{{\text{R}}^{\text{2}}}\text{+4}{{\text{a}}^{\text{2}}}}{\text{4}{{\text{R}}^{\text{2}}}\text{+4}{{\text{a}}^{\text{2}}}}\text{=}\frac{\text{4}}{\text{5}}\Rightarrow \text{a=}\frac{\sqrt{\text{11}}}{\text{2}}\text{R}.$
Suy ra $\frac{{{\text{U}}^{\text{2}}}\text{R}}{{{\text{R}}^{\text{2}}}\text{+}\frac{11{{\text{R}}^{2}}}{4}}\text{=16}\Leftrightarrow {{\text{U}}^{\text{2}}}\text{R}=60{{\text{R}}^{2}}.$
Khi rôto quay với tốc độ 3n vòng/phút thì $\text{P}=\frac{\text{9}{{\text{U}}^{\text{2}}}\text{R}}{{{\text{R}}^{\text{2}}}\text{+9}{{\text{a}}^{\text{2}}}}=\frac{\text{9}\text{.60}{{\text{R}}^{\text{2}}}}{{{\text{R}}^{\text{2}}}\text{+9}\text{.}\frac{11}{4}{{\text{R}}^{2}}}=20,97\text{W}\text{.}$
Chọn C.
Ví dụ 9: Một máy phát điện xoay chiều một pha có điện trở trong không đáng kể. Nối hai cực máy với một mạch RLC nối tiếp. Khi roto có hai cặp cực, quay với tốc độ n vòng/phút thì mạch xảy ra cộng hưởng và ${{\text{Z}}_{\text{L}}}\text{= R,}$ cường độ dòng điện qua mạch là I. Nếu rôto có 4 cặp cực và cũng quay với tốc độ n vòng/phút (từ thông cực đại qua một vòng dây stato không đổi, số vòng dây không đổi) thì cường độ dòng điện hiệu dụng qua mạch là:
A. $\text{2I}\sqrt{13}.$ B. $\frac{\text{2I}}{\sqrt{\text{7}}}.$ C. $\text{2I}.$ D.$\frac{\text{4I}}{\sqrt{13}}.$
HD giải: Ta có: $\text{I=}\frac{\text{U}}{\text{R}}$ (Do ${{\text{Z}}_{\text{L}}}\text{= R}={{\text{Z}}_{\text{C}}}$).
Khi số cặp cực tăng gấp đôi thì ${\omega }’=2\omega \Rightarrow {{\text{Z}}_{\text{L}}}^{\prime }\text{=2}{{\text{Z}}_{\text{L}}}\text{=2R, }{{\text{Z}}_{\text{C}}}^{\prime }\text{=}\frac{{{\text{Z}}_{\text{C}}}}{\text{2}}\text{=}\frac{\text{R}}{\text{2}}.$
Suy ra ${I}’=\frac{2\text{U}}{\sqrt{{{\text{R}}^{2}}+{{\left( {{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{C}}} \right)}^{2}}}}=\frac{2\text{U}}{\sqrt{{{\text{R}}^{2}}+{{\left( \text{2R}-\text{0,5R} \right)}^{2}}}}=\frac{\text{4U}}{\text{R}\sqrt{\text{13}}}\text{=}\frac{\text{4I}}{\sqrt{\text{13}}}\text{.}$ Chọn D.
Ví dụ 10: [Trích đề thi THPT Nguyên Du – Hà Nội 2017] Có hai máy phát điện xoay chiều một pha, các cuộn dây của phần ứng của hai máy giống nhau (bỏ qua điện trở thuần của các cuộn dây và các cuộn dây của phần ứng ghép nối với nhau); số cuộn dây này tỉ lệ với số cặp cực trên mỗi phần cảm (roto); từ trường của mỗi cặp cực trong hai máy cũng như nhau. Máy thứ nhất, roto có hai cặp cực, nối với mạch ngoài là một cuộn dây không thuần cảm; khi cho roto quay với tốc độ n vòng/s thì công suất tỏa nhiệt trên cuộn dây là P và điện áp tức thời hai cực máy phát sớm pha hơn dòng điện tức thời trong mạch $\pi \text{/3}\text{.}$
Máy thứ hai có 4 cặp cực, nếu cũng được nối với cuộn dây trên và roto quay với tốc độ 2n vòng/s thì công suất tỏa nhiệt trên cuộn dây là
A. $\text{256P/49}\text{.}$ B. $\text{32P/19}\text{.}$ C.$\text{6P/19}\text{.}$ D.$\text{64P/49}\text{.}$
HD giải: Với máy (1), khi roto quay với tốc độ n vòng/phút ${{\text{Z}}_{\text{L}}}=\text{R}\sqrt{3}$
Chuẩn hóa $\text{R = 1, }{{\text{Z}}_{\text{L}}}=\sqrt{3}.$Công suất tiêu thụ của mạch $P=\frac{{{\text{U}}^{\text{2}}}}{\text{Z}_{L}^{2}\text{+}{{\text{R}}^{\text{2}}}}\text{R =}\frac{{{\text{U}}^{\text{2}}}}{\text{4}}\text{.}$
Với máy (2), ta để ý rằng số cặp cực gấp đôi (vậy số vòng dây cũng gấp đôi, với giả thuyết số vòng dây tỉ lệ với số cặp cực) nên $\left\{ \begin{array}{} \text{{f}’ = 4f}\Rightarrow {{\text{Z}}_{\text{L}}}^{\prime }=4{{\text{Z}}_{\text{L}}} \\ {} \text{{E}’=}\frac{\text{{N}’BS}.{\omega }’}{\sqrt{2}}=8\text{E} \\ \end{array} \right..$
Công suất tiêu thụ của mạch $\text{P}=\frac{\left( 8{{\text{U}}^{\text{2}}} \right)}{\text{Z}_{L}^{2}\text{+}{{\text{R}}^{\text{2}}}}\text{R=}\frac{\text{64}{{\text{U}}^{\text{2}}}}{{{\left( 4\sqrt{3} \right)}^{\text{2}}}\text{+1}}\text{=}\frac{\text{64}{{\text{U}}^{\text{2}}}}{\text{49R}}=\frac{\text{256}{{\text{U}}^{\text{2}}}}{\text{49}\text{.4R}}=\frac{256}{49}\text{P}.$ Chọn A.
Ví dụ 11: [Trích đề thi THPT Thanh Chương – Nghệ An] Đoạn mạch AB gồm điện trở thuần R mắc nối tiếp với tụ C, được nối vào hai cực của một máy phát điện xoay chiều 1 pha. Bỏ qua điện trở dây nối và cuộn dây máy phát. Khi roto quay đều với tốc độ n vòng/phút thì dung kháng của tụ điện là ${{\text{Z}}_{\text{C1}}}$ và cường độ dòng điện hiệu dụng là $\sqrt{3}\text{ A}.$ Khi roto quay đều với tốc độ 3n vòng/phút thì dung kháng của tụ điện là ${{\text{Z}}_{\text{C2}}}$ và cường độ dòng điện hiệu dụng là $\text{9A}.$ Nếu roto quay với tốc độ 2n vòng/phút thì tổng trở của mạch là:
A. $\frac{3}{2}{{\text{Z}}_{\text{C2}}}.$ B. $\sqrt{2}{{\text{Z}}_{\text{C2}}}.$ C. $\sqrt{32}{{\text{Z}}_{\text{C2}}}.$ D. $\sqrt{\frac{21}{2}}{{\text{Z}}_{\text{C2}}}.$
HD giải: Khi roto quay với tốc độ n vòng/phút, ta chuẩn hóa $R=1,\text{ }{{\text{Z}}_{\text{C1}}}=X.$
Ta có: ${{I}_{1}}=\sqrt{3}=\frac{\text{U}}{\sqrt{1+{{\text{X}}^{2}}}}$
+) Khi roto quay với tốc độ 3n vòng/phút ${{\text{I}}_{2}}=9=\frac{3\text{U}}{\sqrt{1+{{\left( \frac{\text{X}}{3} \right)}^{2}}}}\Rightarrow 3=\frac{1+{{\text{X}}^{2}}}{1+{{\left( \frac{\text{X}}{3} \right)}^{2}}}\Rightarrow \text{X}=\sqrt{3}.$
+) Khi roto quay với tốc độ 2n vòng/phút ${{\text{Z}}_{\text{C3}}}=\frac{\text{X}}{2}=\frac{\sqrt{3}}{2}\Rightarrow \text{Z}=\frac{\sqrt{7}}{2}=\frac{\sqrt{21}}{2}{{\text{Z}}_{\text{C2}}}.$ Chọn D.