BÀI TẬP ĐỒ THỊ ĐIỆN XOAY CHIỀU CÓ ĐÁP ÁN CHI TIẾT
| Bài tập 1: [Trích đề thi THPTQG 2015] Một học sinh xác định điện dung của tụ điện bằng cách đặt điện áp $u={{U}_{0}}\cos \omega t$ (U0 không đổi, $\omega =314$rad/s) vào hai đầu một đoạn mạch gồm tụ điện có điện dung C mắc nối tiếp với biến trở R. Biết $\frac{1}{{{U}^{2}}}=\frac{2}{U_{0}^{2}}+\frac{2}{U_{0}^{2}{{\omega }^{2}}{{C}^{2}}}.\frac{1}{{{R}^{2}}}$; trong đó, điện áp U giữa hai đầu R được đo bằng đồng hồ đo điện đa năng hiện số. Dựa vào kết quả thực nghiệm được cho trên hình vẽ, học sinh này tính được giá trị của C là:
$A.1,{{95.10}^{-3}}F$ $B.5,{{2.10}^{-6}}F$ $C.5,{{2.10}^{-3}}F$ $D.1,{{95.10}^{-6}}F$ |
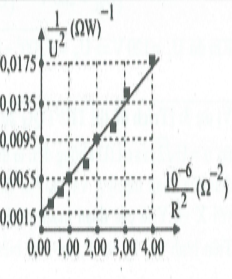 |
HD giải: Mỗi đơn vị trục hoành ứng với $\frac{{{10}^{-6}}}{{{R}^{2}}}({{\Omega }^{-2}})$
Ta có: $\frac{1}{{{U}^{2}}}=\frac{2}{U_{0}^{2}}+\frac{2}{U_{0}^{2}{{\omega }^{2}}{{C}^{2}}}.\frac{1}{{{R}^{2}}}$.
Đặt $y=\frac{1}{{{U}^{2}}};x=\frac{1}{{{R}^{2}}};\frac{2}{U_{0}^{2}}=b;\frac{2}{U_{0}^{2}{{\omega }^{2}}{{C}^{2}}}=a\Rightarrow y=\text{ax}+b$(d).
Do (d) qua 2 điểm $(0;0,0015);({{1.16}^{-6}};0,0055)\Rightarrow \left\{ \begin{array}{} b=0,0015 \\ {} a=4000 \\ \end{array} \right.$
Do đó $\left\{ \begin{array}{} \frac{2}{U_{0}^{2}{{\omega }^{2}}{{C}^{2}}}=4000 \\ {} \frac{2}{U_{0}^{2}}=0,0015 \\ \end{array} \right.\Rightarrow \omega C=\sqrt{\frac{0,0015}{4000}}\Rightarrow C=1,{{95.10}^{-6}}F$. Chọn D.
| Bài tập 2: [Trích đề thi THPTQG 2017] Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch mắc nối tiếp theo thứ tự gồm biến trở R, cuộn cảm L và tụ điện C. Gọi URL là điện áp hiệu dụng ở hai đầu đoạn mạch gồm R và L, Uc là điện áp hiệu dụng hai đầu tụ điện C. Hình bên là đồ thị biểu diễn sự phụ thuộc của URL và UC theo giá trị của biến trở R. Khi giá trị của R bằng 80Ω thì điện áp hiệu dụng ở hai đầu biến trở R có giá trị là: | 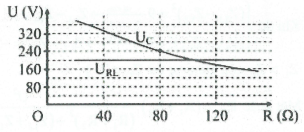 |
| $A.160V$ $B.140V$ $C.120V$ $D.180V$. | |
HD giải: Ta thấy rằng ${{U}_{RL}}=\frac{U.\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\text{=cons}t$ khi R thay đổi.
Do đó ${{R}^{2}}+Z_{L}^{2}={{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}(\forall R)\Leftrightarrow {{Z}_{L}}={{Z}_{C}}-{{Z}_{L}}\Leftrightarrow {{Z}_{C}}=2{{Z}_{L}}\Rightarrow {{U}_{C}}=2{{U}_{L}}$.
Khi $R=80\Omega \Rightarrow \left\{ \begin{array}{} {{U}_{C}}=240V \\ {} {{U}_{RL}}=200V \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{} {{U}_{L}}=0,5{{U}_{C}} \\ {} U_{RL}^{2}=U_{R}^{2}+U_{R}^{2}={{200}^{2}} \\ \end{array} \right.$
Khi đó ${{U}_{L}}=120V\Rightarrow {{U}_{R}}=\sqrt{{{200}^{2}}-{{120}^{2}}}=160V$. Chọn A.
| Bài tập 3: [Trích đề thi THPTQG 2015] Lần lượt đặt điện áp $u=U\sqrt{2}\text{cos}\omega \text{t}$(U không đổi, ω thay đổi được) vào hai đầu của đoạn mạch X và vào hai đầu của đoạn mạch Y; với X và Y là các đoạn mạch có R, L, C mắc nối tiếp. Trên hình vẽ, PX và PY lần lượt biểu diễn quan hệ công suất tiêu thụ của X với ω và của Y với ω. Sau đó, đặt điện áp u lên hai đầu đoạn mạch AB gồm X và Y mắc nối tiếp. Biết cảm kháng của hai cuộn cảm thuần mắc nối tiếp (có cảm kháng ZL1 và ZL2) là ${{\text{Z}}_{L}}={{Z}_{L1}}+{{Z}_{L2}}$ và dung kháng của hai tụ điện mắc nối tiếp (có dung kháng ZC1 và ZC2) là ${{\text{Z}}_{C}}={{Z}_{C1}}+{{Z}_{C2}}$. Khi$\omega ={{\omega }_{2}}$, công suất tiêu thụ của đoạn mạch AB có giá trị gần giá trị nào nhất sau đây?
$A.14\text{W}$ $B.10\text{W}$ $C.22W$ $D.18W$ |
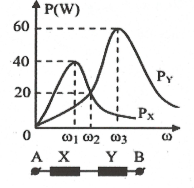 |
HD giải: Dựa vào đồ thị ta thấy $\omega ={{\omega }_{1}}$ thì ${{P}_{Xm\text{ax}}}=\frac{{{U}^{2}}}{{{R}_{1}}^{2}}=40$
Khi $\omega ={{\omega }_{3}}$ thì ${{P}_{Ym\text{ax}}}=\frac{{{U}^{2}}}{{{R}^{2}}}=60$. Do đó $\frac{{{R}_{2}}}{{{R}_{1}}}=\frac{2}{3}$.
Khi $\omega ={{\omega }_{2}}$ta có: ${{P}_{x}}={{R}_{1}}.\frac{40{{R}_{1}}}{R_{1}^{2}+{{({{Z}_{L1}}-
{{Z}_{C1}})}^{2}}}=20;{{P}_{y}}={{R}_{2}}.\frac{60{{R}_{2}}}{R_{2}^{2}+{{({{Z}_{L2}}-{{Z}_{C2}})}^{2}}}=20$.
Để đơn giản bài toán ta chuẩn hóa ${{R}_{1}}=3\Rightarrow {{R}_{2}}=2.$
Khi đó $\left\{ \begin{array}{} {{({{Z}_{L1}}-{{Z}_{C1}})}^{2}}=9\xrightarrow{{{\omega }_{1}}<{{\omega }_{2}}}{{Z}_{L1}}-{{Z}_{C1}}=3 \\ {} {{({{Z}_{L2}}-{{Z}_{C2}})}^{2}}=8\xrightarrow{{{\omega }_{2}}{{Z}_{C}}$ còn giảm ω thì ${{Z}_{C}}<{{Z}_{L}}$)
Mặt khác ${{P}_{AB}}=({{R}_{1}}+{{R}_{2}}).\frac{{{U}^{2}}}{{{({{R}_{1}}+{{R}_{2}})}^{2}}+{{({{Z}_{L1}}+{{Z}_{L2}}-{{Z}_{C1}}-{{Z}_{C2}})}^{2}}}$
$=5.\frac{40.3}{{{5}^{2}}+{{(3-2\sqrt{2})}^{2}}}=23,97W$. Chọn C.
| Bài tập 4: Lần lượt đặt vào hai đầu đoạn mạch xoay chiều gồm biến trở R, cuộn cảm thuần L và tụ điện C nối tiếp hai điện áp xoay chiều ${{u}_{1}}={{U}_{1}}\sqrt{2}\text{cos(}{{\omega }_{1}}t+{{\varphi }_{1}})V$và${{u}_{2}}={{U}_{2}}\sqrt{2}\text{cos(}{{\omega }_{2}}t+{{\varphi }_{2}})V$người ta thu được đồ thị công suất toàn mạch theo biến trở R như hình vẽ. Biết rằng ${{P}_{2\max }}=x$. Giá trị của x gần giá trị nào sau đây nhất?
$A.112,5\Omega $ $B.106\Omega $ $C.101\Omega $ $D.108\Omega $ |
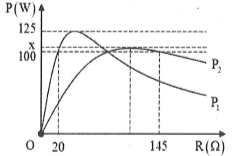 |
HD giải: Xét P1: Khi $R=20\Omega $ và $R=a$ thì ${{P}_{1}}=\frac{U_{1}^{2}}{20+a}=100W(a>20)(1).$
Xét P2: Khi $R=145\Omega $ và $R=a$ thì ${{P}_{2}}=\frac{U_{2}^{2}}{145+a}=100W.$
Mặt khác ${{P}_{1m\text{ax}}}=\frac{U_{1}^{2}}{2\sqrt{20a}}=125W(2);{{P}_{2m\text{ax}}}=\frac{U_{2}^{2}}{2\sqrt{145a}}$
Từ (1) và (2) suy ra $\frac{250\sqrt{20a}}{20+a}=100\Rightarrow \left[ \begin{array}{} \sqrt{20a}=40 \\ {} \sqrt{20a}=10 \\ \end{array} \right.\Rightarrow \left[ \begin{array}{} a=80 \\ {} a=5(lo\text{ai)} \\ \end{array} \right.$
Khi đó $U_{2}^{2}=22500\Rightarrow x=\frac{22500}{2\sqrt{145.80}}=104,45.$ Chọn B.
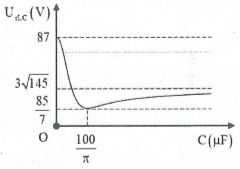
| Bài tập 5: Cho mạch điện gồm R, L và C theo thứ tự nối tiếp, cuộn dây có điện trở r. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số $f=50Hz$. Cho điện dung C thay đổi người ta thu được đồ thị liên hệ giữa điện áp hiệu dụng hai đầu mạch chứa cuộn dây và tụ điện UrLC với điện dung C của tụ điện như hình vẽ bên. Điện trở r có giá trị bằng:
$A.50\Omega $ $B.120\Omega $ $C.90\Omega $ $D.30\Omega $ |
 |
HD giải: Biểu thức điện áp giữa hai đầu LC: ${{U}_{rLC}}=\frac{U\sqrt{{{r}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}{\sqrt{{{(R+r)}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}.$
Khi $C\to 0\Rightarrow {{Z}_{C}}=+\infty \Rightarrow \sqrt{\frac{{{r}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{{{(R+r)}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\approx 1\Rightarrow {{U}_{rLC}}=U=87V(1).$
Khi $C=\frac{100}{\pi }\mu F\Rightarrow {{Z}_{C}}=100\Omega $ mạch có cộng hưởng ${{Z}_{L}}={{Z}_{C}}=100\Omega \Rightarrow {{U}_{rLC}}=\frac{\text{Ur}}{R+r}=\frac{87}{5}(2)$
Khi $C\to +\infty $ thì ${{Z}_{C}}\to 0\Rightarrow {{U}_{rLC}}=\frac{U\sqrt{{{r}^{2}}+Z_{L}^{2}}}{\sqrt{{{(R+r)}^{2}}+Z_{L}^{2}}}=3\sqrt{145}(3).$
Từ (1) và (2) suy ra $\frac{r}{R+r}=\frac{1}{5}\Rightarrow R=4r$
Khi đó $(3)\Rightarrow \frac{87\sqrt{{{r}^{2}}+{{100}^{2}}}}{\sqrt{25{{r}^{2}}+{{100}^{2}}}}=3\sqrt{145}\xrightarrow{CALC}r=50\Omega .$ Chọn A.
| Bài tập 6: [Trích đề thi Sở GD-ĐT Quảng Ninh 2017] Cho đoạn mạch AB không phân nhánh gồm đoạn mạch AM chứa cuộn cảm thuần, đoạn mạch MN chứa điện trở thuần và đoạn mạch NB chứa tụ điện. Đặt điện áp $u={{U}_{0}}\text{cos(}\omega \text{t+}\varphi \text{)V}$ (trong đó U0, ω, $\varphi $ xác định) vào hai đầu mạch AB. Khi đó điện áp tức thời hai đầu đoạn mạch AN, MB lần lượt là uAN và uMB được biểu thị ở hình vẽ. Hệ số công suất của đoạn mạch MB là:
$A.0,65.$ $B.0,33.$ $C.0,74.$ $D.0,50.$ |
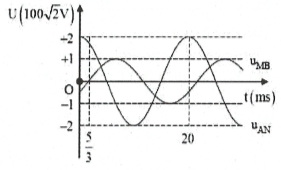 |
HD giải: Từ đồ thị, ta có: $\text{T=20}\text{.1}{{\text{0}}^{-3}}s\Rightarrow \omega =100\pi rad/s$
${{u}_{AN}}=200\sqrt{2}\text{cos(100}\pi \text{t)V}$
Tại $\text{t=}\frac{5}{3}ms\Rightarrow \left\{ \begin{array}{} {{u}_{MB}}=0 \\ {} {{u}_{MB}}\uparrow \\ \end{array} \right.\Rightarrow {{\varphi }_{MB}}=\frac{-\pi }{2}.$
Do đó ${{\varphi }_{0MB}}=-\frac{\pi }{2}-\frac{5}{3}{{.10}^{-3}}.100\pi =-\frac{2\pi }{3}.$
Ta có: $\left\{ \begin{array}{} AB=\sqrt{O{{A}^{2}}+O{{B}^{2}}-2OA.OBc\text{os12}{{\text{0}}^{0}}} \\ {} {{S}_{OAB}}=\frac{1}{2}OA.OB=\frac{1}{2}{{U}_{R}}.AB\Rightarrow {{U}_{R}}=\frac{100\sqrt{21}}{7}. \\ \end{array} \right.$
$\text{cos}{{\varphi }_{MB}}=c\text{os}{{\varphi }_{RC}}=\frac{{{U}_{R}}}{OB}=\frac{\sqrt{21}}{7}=0,65.$ Chọn A.
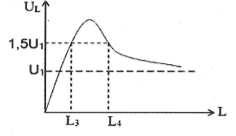
| Bài tập 7: [Trích đề thi Chuyên Phan Bội Châu lần 2017] Đặt vào hai đầu đoạn mạch RLC mắc nối tiếp một điện áp xoay chiều với giá trị hiệu dụng và tần số không đổi. Biết cuộn cảm thuần có độ tự cảm L thay đổi được. Khi $L={{L}_{1}}$và $L={{L}_{2}}$ thì điện áp hiệu dụng hai đầu tụ điện có giá trị như nhau. Biết ${{L}_{1}}+{{L}_{2}}=0,8H$. Đồ thị biểu diễn điện áp UL vào L như hình vẽ. Tổng giá trị ${{L}_{3}}+{{L}_{4}}$ gần giá trị nào nhất sau đây:
$A.1,57H.$ $B.0,98H.$ $C.1,45H.$ $D.0,64H.$ |
 |
HD giải: Hai giá trị của L làm UC không đổi suy ra ${{Z}_{L1}}+{{Z}_{L2}}=2{{Z}_{C}}$
Ta có ${{U}_{L}}=\frac{U{{Z}_{L}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}$
Khi $L\to +\infty \Rightarrow {{U}_{L}}=U={{U}_{1}}$ (vì $\frac{Z_{L}^{2}}{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}\approx 1$)
L3; L4 là hai giá trị làm cho UL không đổi nên
${{U}_{L}}={{Z}_{L}}.\frac{{{U}_{1}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}=1,5{{U}_{1}}\Leftrightarrow {{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}=\frac{1}{1,{{5}^{2}}}Z_{L}^{2}$
$\Leftrightarrow \left( 1-\frac{1}{1,{{5}^{2}}} \right)Z_{L}^{2}-2{{Z}_{L}}{{Z}_{C}}+{{R}^{2}}+Z_{C}^{2}=0$Theo Viet ta có: ${{Z}_{L3}}+{{Z}_{L4}}=\frac{2{{Z}_{C}}}{1-\frac{1}{1,{{5}^{2}}}}$
$\Leftrightarrow {{Z}_{L3}}+{{Z}_{L4}}=\frac{{{Z}_{L1}}+{{Z}_{L2}}}{1-\frac{1}{1,{{5}^{2}}}}\Leftrightarrow {{L}_{3}}+{{L}_{4}}=\frac{{{L}_{1}}+{{L}_{2}}}{1-\frac{1}{1,{{5}^{2}}}}=1,44.$ Chọn C.
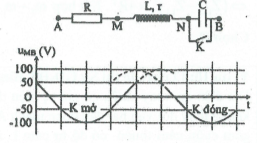
| Bài tập 8: [Trích đề thi THPT QG năm 2017] Đặt điện áp $u=U\sqrt{2}\text{cos}\omega \text{t}$ (U và ω không đổi) vào hai đầu đoạn mạch AB. Hình vẽ bên là sơ đồ mạch điện và một phần đồ thị biểu diễn sự phụ thuộc của điện áp uMB giữa hai điểm M, B theo thời gian t khi K mở và khi K đóng. Biết điện trở $\text{R=2r}$. Giá trị của U là:
$A.193,2V.$ $B.187,1V.$ $C.136,6V.$ $D.122,5V.$ |
 |
HD giải: Ta có: ${{U}_{MB1}}={{U}_{MB2}}\Rightarrow {{Z}_{MB1}}.\frac{U}{{{Z}_{1}}}={{Z}_{MB2}}.\frac{U}{{{Z}_{2}}};{{Z}_{AB}}=R+r=3r.$
Chú ý: Chỉ pha ban đầu của uAB không đổi, pha ban đầu của i thay đổi.
$\Leftrightarrow \sqrt{\frac{{{r}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{{{(R+r)}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}=\sqrt{\frac{{{r}^{2}}+Z_{L}^{2}}{{{(R+r)}^{2}}+Z_{L}^{2}
}}\Rightarrow {{({{Z}_{L}}-{{Z}_{C}})}^{2}}=Z_{L}^{2}\Leftrightarrow {{Z}_{C}}=2{{Z}_{L}}.$
Dựa vào đồ thị ta thấy $T=6$ô và uMB2 sớm hơn uMB1 một ô tương ứng là $\frac{T}{6}$ ứng với góc $\frac{\pi }{3}$ hay ${{\varphi }_{MB2}}-{{\varphi }_{MB1}}=\frac{\pi }{3}$.
Vẽ giãn đồ vecto như hình vẽ:
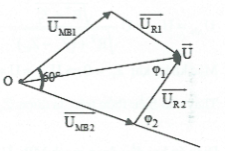
Khi K đóng ta có: $\left\{ \begin{array}{} \tan {{\varphi }_{2}}=\frac{{{Z}_{L}}}{r} \\ {} \tan {{\varphi }_{1}}=\frac{{{Z}_{L}}}{R+r}=\frac{{{Z}_{L}}}{3r} \\ \end{array} \right.\Rightarrow \tan {{\varphi }_{2}}=3\tan {{\varphi }_{1}}$
Kết hợp
${{\varphi }_{2}}-{{\varphi }_{1}}={{30}^{0}}\Rightarrow \left\{ \begin{array}{} {{\varphi }_{2}}={{60}^{0}} \\ {} {{\varphi }_{1}}={{30}^{0}} \\
\end{array} \right.\Rightarrow \frac{{{U}_{MB2}}}{\sin {{30}^{0}}}=\frac{U}{\sin {{120}^{0}}}\Rightarrow U={{U}_{MB2}}\sqrt{3}=50\sqrt{6}V.$ Chọn D.
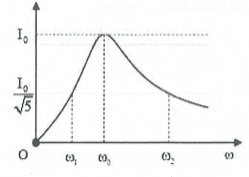
| Bài tập 9: [Trích đề thi Chuyên Quốc Học Huế 2017] Cho một mạch điện xoay chiều RLC mắc nối tiếp. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều $u=Uc\text{os(}\omega \text{t)V}$, ω có thể thay đổi. Đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện hiệu dụng vào ω như hình vẽ. Với ${{\omega }_{2}}-{{\omega }_{1}}=\frac{400}{\pi }rad/s,L=\frac{3\pi }{4}H.$ Giá trị của R là:
$A.200\Omega .$ $B.100\Omega .$ $C.160\Omega .$ $D.150\Omega .$ |
 |
HD giải: Với hai giá trị của tần số cho cùng dòng điện hiệu dụng trong mạch, ta luôn có:
${{\omega }_{1}}{{\omega }_{2}}=\omega _{0}^{2}=\frac{1}{\sqrt{LC}}\Rightarrow {{Z}_{L1}}={{Z}_{C2}}$
Từ hình vẽ ta có: $\frac{U}{\sqrt{{{R}^{2}}+{{({{Z}_{L2}}-{{Z}_{C2}})}^{2}}}}=\frac{U}{R\sqrt{5}}\Leftrightarrow {{R}^{2}}+{{({{Z}_{L2}}-{{Z}_{C2}})}^{2}}=5{{R}^{2}}$
$\Leftrightarrow {{({{Z}_{L2}}-{{Z}_{L1}})}^{2}}=4{{R}^{2}}.$ Kết hợp ${{\omega }_{2}}-{{\omega }_{1}}=\frac{400}{\pi }rad/s\Rightarrow L({{\omega }_{2}}-{{\omega }_{1}})=2R\Rightarrow R=\frac{\frac{400}{\pi }.\frac{3\pi }{4}}{2}=150\Omega .$ Chọn D.
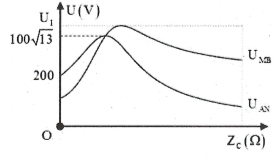
| Bài tập 10: [Trích đề thi Sở GD-ĐT Bình Phước] Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không thay đổi vào hai đầu đoạn mạch AB theo thứ tự gồm cuộn cảm thuần có độ tự cảm L xác định, điện trở thuần $R=200\Omega $ và tụ điện có điện dung C thay đổi được ghép nối tiếp. Gọi M là điểm nối giữa L với R; N là điểm nối giữa R với C. Khi C thay đổi thì đồ thị biểu diễn điện áp hiệu dụng hai đầu đoạn mạch AN và MB theo dung kháng ZC được biểu diễn như hình vẽ. Giá trị U1 bằng:
$A.401V.$ $B.100\sqrt{17}V.$ $C.400V.$ $D.100\sqrt{15}V.$ |
 |
HD giải: Điện áp hai đầu đoạn mạch AN:
${{U}_{AN}}={{U}_{RL}}=U\frac{\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\xrightarrow[{{U}_{AN}}={{U}_{ANm\text{ax}}}]{{{Z}_{L}}={{Z}_{C}}}100\sqrt{13}=U\frac{\sqrt{{{R}^{2}}+Z_{L}^{2}}}{R}$
Mặt khác, khi ${{Z}_{C}}=0\Rightarrow {{U}_{AN}}=U=200V.$
Thay vào biểu thức trên, ta được ${{Z}_{L}}=\frac{3}{2}R=300\Omega .$
Điện áp hai đầu đoạn mạch MB: ${{U}_{MB}}={{U}_{RC}}=U\frac{\sqrt{{{R}^{2}}+Z_{C}^{2}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}$
Áp dụng ${{U}_{RCm\text{ax}}}\to \left\{ \begin{array}{} {{Z}_{C}}=\frac{{{Z}_{L}}+\sqrt{Z_{L}^{2}+4{{R}^{2}}}}{2} \\ {} {{U}_{RCm\text{ax}}}=\frac{U}{R}.{{Z}_{C}}=\frac{U}{R}.\frac{{{Z}_{L}}+\sqrt{Z_{L}^{2}+4{{R}^{2}}}}{2}=400V \\ \end{array} \right.$ . Chọn C.
| Bài tập 11: [Trích đề thi Sở Bắc Ninh 2017] Cho mạch điện xoay chiều gồm một điện trở thuần, một cuộn cảm thuần và một tụ điện mắc nối tiếp. Đặt vào hai đầu mạch điện áp xoay chiều có giá trị hiệu dụng không đổi và tần số góc ω thay đổi được. Điện áp hiệu dụng giữa hai bản tụ điện và điện áp hiệu dụng hai đầu cuộn cảm lần lượt là UC, UL phụ thuộc vào ω, chúng được biểu diễn bằng các đồ thị như hình vẽ, tương ứng với các đường UC, UL. Khi $\omega ={{\omega }_{1}}$ thì UC đạt cực đại Um và khi $\omega ={{\omega }_{2}}$ thì UL đạt cực đại Um. Giá trị Um gần giá trị nào nhất sau đây:
$A.130V.$ $B.140V.$ $C.150V.$ $D.160V.$ |
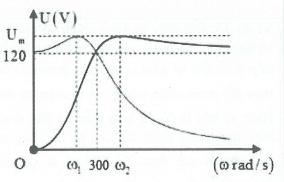 |
HD giải: Khi $\omega =0\Rightarrow {{Z}_{L}}=0,{{Z}_{C}}=\infty \Rightarrow {{U}_{C}}=\frac{U{{Z}_{C}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\to U$
Khi $\omega =300rad/s$ ta có: ${{U}_{L}}={{U}_{C}}\Rightarrow \omega =\frac{1}{\sqrt{LC}}\Rightarrow \frac{L}{C}={{Z}_{L}}{{Z}_{C}}.$
Mặt khác khi đó: ${{U}_{L}}={{U}_{C}}=U={{U}_{R}}\Rightarrow {{Z}_{L}}={{Z}_{C}}=R.$
${{U}_{Cm\text{ax}}}={{U}_{Lm\text{ax}}}=\frac{2UL}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}=\frac{2U}{\sqrt{4\frac{C}{L}{{R}^{2}}-{{\left( {{R}^{2}}\frac{C}{L} \right)}^{2}}}}=\frac{2U}{\sqrt{\frac{4{{R}^{2}}}{{{Z}_{L}}{{Z}_{C}}}-{{\left( \frac{{{R}^{2}}}{{{Z}_{L}}{{Z}_{C}}} \right)}^{2}}}}=\frac{240}{\sqrt{3}}=138V.$Chọn B.
| Bài tập 12: Đặt điện áp $u=U\sqrt{2}\text{cos}\omega \text{t}$ (U và ω không đổi) vào hai đầu đoạn mạch AB nối tiếp gồm cuộn dây thuần cảm có độ tự cảm L, điện trở R và tụ điện có dung kháng ZC thay đổi. Đồ thị phụ thuộc ZC của điện áp hiệu dụng trên đoạn RC như hình vẽ. Điện áp hiệu dụng cực đại trên tụ gần giá trị nào nhất sau đây?
$A.250V.$ $B.280V.$ $C.200V.$ $D.350V.$ |
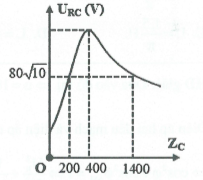 |
HD giải: Khi ${{\text{Z}}_{Cm\text{ax}}}=400\Omega ,{{\text{Z}}_{Cm\text{ax}}}=\frac{{{Z}_{L}}+\sqrt{4{{R}^{2}}+Z_{L}^{2}}}{2}\Leftrightarrow 800={{Z}_{L}}+\sqrt{4{{R}^{2}}+Z_{L}^{2}}$ (1)
Có ${{Z}_{C1}}=200\Omega $ và ${{Z}_{C2}}=1400\Omega $ thì ${{U}_{C1}}={{U}_{C2}}\Leftrightarrow \frac{\sqrt{{{200}^{2}}+{{R}^{2}}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-
200)}^{2}}}}=\frac{\sqrt{{{1400}^{2}}+{{R}^{2}}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-1400)}^{2}}}}(2)$
Từ (1) và (2) $\Rightarrow {{Z}_{L}}=300\Omega $ và $R=200\Omega \Rightarrow U=200V.$
Điện áp hiệu dụng cực đại trên tụ là ${{U}_{Cm\text{ax}}}=\frac{U.\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}\approx 360\Omega .$. Chọn D.
| Bài tập 13: Đặt điện áp xoay chiều có giá trị hiệu dụng U và tần số f không đổi vào hai đầu đoạn mạch AB mắc nối tiếp theo thứ tự gồm cuộn cảm thuần có cảm kháng ZL thay đổi được, điện trở R và tụ điện có dung kháng ZC. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng trên đoạn RC và hệ số công suất cos$\varphi $ của đoạn mạch AB theo ZL. Giá trị R gần nhất với giá trị nào sau đây:
$A.50\Omega .$ $B.26\Omega .$ $C.40\Omega .$ $D.36\Omega .$ |
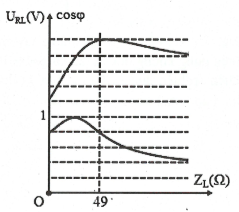 |
HD giải: Dựa vào đồ thị $\Rightarrow $Đường màu đỏ (trên) biểu diễn ZL theo URL và đường màu xanh (dưới) biểu diễn ZL theo cos$\varphi $. Tại ${{Z}_{L}}=0\Rightarrow c\text{os}\varphi \text{=}\frac{4}{5}\Leftrightarrow \tan \varphi =\frac{3}{4}\Leftrightarrow \frac{{{Z}_{C}}}{R}=\frac{3}{4}$
Khi ${{Z}_{L}}=49\Omega \Rightarrow {{U}_{Lm\text{ax}}}\Rightarrow {{Z}_{L}}=\frac{{{Z}_{C}}+\sqrt{Z_{C}^{2}+4{{R}^{2}}}}{2}\Leftrightarrow
49=\frac{\frac{4}{3}R+\sqrt{{{\left( \frac{4}{3}R \right)}^{2}}+4{{R}^{2}}}}{2}\Leftrightarrow R\approx 26\Omega .$. Chọn B.
| Bài tập 14: Đặt điện áp xoay chiều vào hai đầu đoạn mạch AB như hình vẽ (cuộn dây thuần cảm L) thì điện áp tức thời hai đầu mạch AB (u) và hai đầu đoạn mạch AM (uAB) mô tả bởi đồ thị như hình vẽ, dòng điện trong mạch có giá trị hiệu dụng 1A. Tính L
$A.L=\frac{0,5}{\pi }H.$ $B.L=\frac{15}{\pi }H.$ $C.L=\frac{1,5}{\pi }H.$ $D.L=\frac{2}{\pi }H.$ |
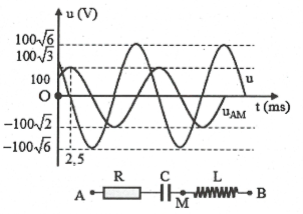 |
HD giải: Dựa vào đồ thị $\Rightarrow u=100\sqrt{6}\text{cos}\left( 100\pi t+\frac{\pi }{4} \right)V$ và ${{u}_{AM}}=100\sqrt{2}\text{cos}\left( 100\pi t-\frac{\pi }{4} \right)V$
Điện áp hai đầu mạch và điện áp đoạn AM lệch pha nhau góc $\frac{\pi }{2}rad$
$\Rightarrow c\text{o}{{\text{s}}^{2}}\varphi +c\text{o}{{\text{s}}^{2}}{{\varphi }_{AM}}=1\Leftrightarrow \frac{U_{R}^{2}}{{{U}^{2}}}+\frac{U_{R}^{2}}{U_{AM}^{2}}=1\Leftrightarrow \frac{U_{R}^{2}}{{{\left( 100\sqrt{3}\right)}^{2}}}+\frac{U_{R}^{2}}{{{100}^{2}}}=1\Leftrightarrow {{U}_{R}}=50\sqrt{3}V$
$\Rightarrow R=\frac{{{U}_{R}}}{I}=50\sqrt{3}\Omega $ và ${{Z}_{AM}}=100\Omega \Rightarrow {{Z}_{C}}=50\Omega .$. Lại có $Z=100\sqrt{3}\Omega $
$\Rightarrow {{Z}_{L}}=200\Omega \Rightarrow L=\frac{2}{\pi }H.$ Chọn D.
