LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. Mạch R-L-C có L thay đổi (các đại lượng khác không đổi).
a. Phương pháp giải
| Xét bài toán:
Cho mạch điện R-L-C mắc nối tiếp cuộn dây thuần cảm có L thay đổi (các đại lượng khác không đổi). Tìm L để.
a)${{\text{I}}_{\text{max}}}\text{,}{{\text{U}}_{\text{Rmax}}}\text{,}{{\text{U}}_{\text{Cmax}}}\text{,}{{\text{P}}_{\text{max}}}$. b) .${{\text{U}}_{\text{Lmax}}}$ c) ${{\text{U}}_{\text{RLmax}}}$. |
Lời giải chi tiết
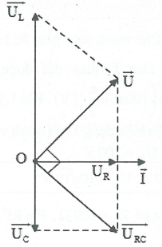
a) Ta có $I=\frac{U}{Z}=\frac{U}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}\le \frac{U}{R}$.
Dấu bằng xảy ra khi ${{Z}_{L}}={{Z}_{C}}\Leftrightarrow L=\frac{1}{{{\omega }^{2}}C}\Rightarrow {{I}_{\max }}=\frac{U}{R}$.
Khi đó: ${{U}_{R\max }}={{I}_{\max }}R=U,\ {{U}_{C\max }}={{Z}_{C}}.{{I}_{\max }}={{Z}_{C}}.\frac{U}{R},\,{{P}_{\max }}=RI_{\max }^{2}=R.\frac{{{U}^{2}}}{{{R}^{2}}}=\frac{{{U}^{2}}}{R}.$
b) Cách 1: Ta có ${{U}_{L}}=\frac{{{Z}_{L}}.U}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{U}{\sqrt{\frac{{{R}^{2}}+Z_{C}^{2}}{Z_{L}^{2}}-\frac{2{{Z}_{C}}}{{{Z}_{L}}}+1}}.$
Đặt $x=\frac{1}{{{Z}_{L}}}$suy ra $\frac{{{R}^{2}}+Z_{C}^{2}}{Z_{L}^{2}}-\frac{2{{Z}_{C}}}{{{Z}_{L}}}+1=\left( {{R}^{2}}+Z_{C}^{2} \right){{x}^{2}}-2{{Z}_{C}}.x+1=f\left( x \right)$.
Do $f\left( x \right)$ có $a={{R}^{2}}+Z_{C}^{2}>0$ nên $\text{Min}\ \text{f}\left( x \right)=f\left( \frac{-b}{2a} \right)=f\left( \frac{{{Z}_{C}}}{{{R}^{2}}+Z_{C}^{2}} \right)=\frac{-\Delta }{4a}=\frac{{{R}^{2}}}{{{R}^{2}}+Z_{C}^{2}}.$
Vậy, ${{U}_{L\max }}\Leftrightarrow \left\{ \begin{array}{} {{Z}_{L}}=\frac{{{R}^{2}}+Z_{C}^{2}}{{{Z}_{C}}} \\ {} {{U}_{L\max }}=\frac{U}{R}\sqrt{{{R}^{2}}+Z_{C}^{2}} \\ \end{array} \right..$
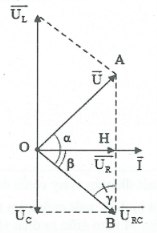
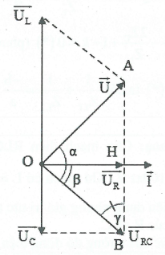
Cách 2: Sử dụng giãn đồ vecto.
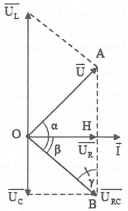
Ta có: $\cos \beta =\frac{{{U}_{R}}}{{{U}_{RC}}}=\frac{R}{\sqrt{{{R}^{2}}+Z_{C}^{2}}}$.
Áp dụng định lý hàm sin trong $\Delta OAB$ta có:
$\frac{{{U}_{L}}}{\sin \left( \alpha +\beta \right)}=\frac{U}{\sin \gamma }=\frac{U}{\cos \beta }=\frac{U\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}.$
Suy ra ${{U}_{L}}=\frac{U\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}\sin \left( \alpha +\beta \right)\le \frac{U\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}.$
Dấu bằng xảy ra $\Leftrightarrow \alpha +\beta =\frac{\pi }{2}\Leftrightarrow \overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}.$
Áp dụng hệ thức lượng trong tam giác vuông.
Ta có: $O{{B}^{2}}=AB.HB\Rightarrow {{U}_{L}}.{{U}_{C}}=U_{R}^{2}+U_{C}^{2}$
$\Rightarrow {{Z}_{L}}.{{Z}_{C}}={{R}^{2}}+Z_{C}^{2}.$
Vậy ${{U}_{L\max }}=\frac{U}{R}\sqrt{{{R}^{2}}+Z_{C}^{2}}\ {{Z}_{L}}=\frac{{{R}^{2}}+Z_{C}^{2}}{{{Z}_{C}}}$.
Chú ý: Khi ${{U}_{L\max }}$ta có: $\ \overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}\ $nên trong tam giác OAB vuông tại O có đường cao OH ta có:
+) Định lý Pytago: ${{U}^{2}}+U_{RC}^{2}=U_{L}^{2}.$
+) $\frac{1}{{{h}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}\Rightarrow \frac{1}{U_{R}^{2}}=\frac{1}{{{U}^{2}}}+\frac{1}{U_{RC}^{2}}.$
+) $O{{A}^{2}}=AB.HA\Rightarrow {{U}^{2}}={{U}_{L}}.\left( {{U}_{L}}-{{U}_{C}} \right).$
+) $OH.AB=OA.OB={{U}_{R}}.{{U}_{L}}={{U}_{RC}}.U=2{{S}_{OAB}}.$
Cách 3: Sử dụng phép biến đổi lượng giác:
Ta có: $\tan \varphi =\frac{{{Z}_{L}}-{{Z}_{C}}}{R}\Rightarrow {{Z}_{L}}={{Z}_{C}}+R\tan \varphi .$
Khi đó ${{U}_{L}}=I.{{Z}_{L}}=\frac{U}{Z}.{{Z}_{L}}=\frac{U}{\frac{R}{\cos \varphi }}\left( {{Z}_{C}}+R\tan \varphi \right).$
$=\frac{U}{R}\left( {{Z}_{C}}\cos \varphi +R\sin \varphi \right)\le \frac{U}{R}\sqrt{Z_{C}^{2}+{{R}^{2}}}$(bất đẳng thức $a\sin x+b\cos x\le \sqrt{{{a}^{2}}+{{b}^{2}}}).$
c) Ta có: ${{U}_{RL}}=\frac{{{Z}_{RL}}.U}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{U}{\sqrt{1+\frac{Z_{C}^{2}-2{{Z}_{L}}{{Z}_{C}}}{{{R}^{2}}+Z_{L}^{2}}}}.$
Ta khảo sát hàm số $y=1+\frac{Z_{C}^{2}-2{{Z}_{L}}{{Z}_{C}}}{{{R}^{2}}+Z_{L}^{2}}.$Khảo sát và tìm GTNN của $y$ta được:
${{U}_{RL\max }}$$\to \left\{ \begin{array}{} {{Z}_{L}}=\frac{{{Z}_{C}}+\sqrt{Z_{C}^{2}+4{{R}^{2}}}}{2} \\ {} {{U}_{RL\max }}=\frac{U}{R}.{{Z}_{L}}=\frac{U}{R}.\frac{{{Z}_{C}}+\sqrt{Z_{C}^{2}+4{{R}^{2}}}}{2} \\ \end{array} \right.$.
${{Z}_{L}}=0\Leftrightarrow {{U}_{RL}}={{U}_{RL\min }}=\frac{U.R}{\sqrt{{{R}^{2}}+Z_{C}^{2}}}{{Z}_{L}}\to +\infty \Rightarrow {{U}_{RL}}\to U.$
a. Bài tập minh họa:
| Cho mạnh điện RLC có $R=100\sqrt{3}\Omega ,\ C=\frac{{{10}^{-4}}}{2\pi }\left( F \right).$ Cuộn dây thuần cảm có độ tự cảm L thay đổi được. Điện áp giữa hai đầu đoạn mạch là
$u=200\cos \left( 100\pi t \right)\,\,\text{V}.$ Xác định độ tự cảm của cuộn dây trong các trường hợp sau? a) Hệ số công suất của mạch $cos\varphi =1.$ b) Hệ số công suất của mạch $\cos \varphi =\frac{\sqrt{3}}{2}.$ c) Điện áp hiệu dụng trên cuộn cảm L là cực đại. d) Điện áp giữa hai đầu đoạn mạch RL; RC cực đại. |
Lời giải chi tiết
Ta có ${{Z}_{C}}=\frac{1}{\omega C}=200\ \Omega .$
a) Từ $\cos \varphi =1\ $mạch có cộng hưởng điện. Khi đó ${{Z}_{L}}={{Z}_{C}}=200\ \Omega \Rightarrow L=\frac{2}{\pi }H$
b) Khi $\cos \varphi =\frac{\sqrt{3}}{2}\Leftrightarrow \frac{R}{Z}=\frac{\sqrt{3}}{2}\Leftrightarrow 4{{R}^{2}}=3{{Z}^{2}}=3\left[ {{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}} \right]\Rightarrow {{R}^{2}}=3{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}$
Thay số ta được ${{Z}_{L}}-{{Z}_{C}}=\pm \frac{R}{\sqrt{3}}=\pm 100\Rightarrow \left[ \begin{array}{} {{Z}_{L}}=300\Omega \\ {} {{Z}_{L}}=100\Omega \\ \end{array} \right.\Leftrightarrow \left[ \begin{array}{} L=\frac{3}{\pi }H \\ {} L=\frac{1}{\pi }H \\ \end{array} \right.$
c) Theo chứng minh trên, ${{U}_{L}}$đạt cực đại khi $\ {{Z}_{L}}=\frac{{{R}^{2}}+Z_{C}^{2}}{{{Z}_{C}}}=350\Omega \Rightarrow L=\frac{35}{100\pi }H$
Giá trị cực đại là ${{\left( {{U}_{L}} \right)}_{\max }}=\frac{U}{R}\sqrt{{{R}^{2}}+Z_{C}^{2}}=\frac{100\sqrt{42}}{3}V.$
d) Khi L biến thiên để ${{\left( {{U}_{RL}} \right)}_{\max }}$thì ta có $\ \left\{ \begin{array}{} {{Z}_{L}}=\frac{{{Z}_{C}}+\sqrt{Z_{C}^{2}+4{{R}^{2}}}}{2}=232\Omega \\ {} {{\left( {{U}_{RL}} \right)}_{\max }}=U\frac{{{Z}_{L}}}{R}=189,4\ V \\ \end{array} \right.$
Lại có, ${{U}_{RC}}=I{{Z}_{RC}}\Rightarrow {{\left( {{U}_{RC}} \right)}_{\max }}\Leftrightarrow \left\{ \begin{array}{} {{Z}_{L}}={{Z}_{C}}=200\Omega \\ {} {{\left( {{U}_{RC}} \right)}_{\max }}=\frac{U}{R}\sqrt{{{R}^{2}}+Z_{C}^{2}}=\frac{100\sqrt{42}}{3}\,V \\ \end{array} \right..$
a. Bài tập luyện tập mạch R-L-C có L thay đổi (các đại lượng khác không đổi) có đáp án chi tiết
| Bài tập 1: Đặt điện áp $u=100\sqrt{2}\cos 100\pi t\left( V \right)$ vào hai đầu đoạn mạch nối tiếp cuộn cảm thuần có độ tự cảm L thay đổi được, tụ điện có dung kháng $36\Omega $ và điện trở $R=48\Omega $. Thay đổi L để điện áp hiệu dụng trên cuộn dây đạt giá trị cực đại. Lúc này cảm kháng và điện áp hiệu dụng trên L lần lượt là:
A. $100\Omega \ \text{v }\!\!\mu\!\!\text{ }\,125\ V$ B. $100\Omega \ \text{v }\!\!\mu\!\!\text{ }\,125\sqrt{2}\ V$ C. $75\Omega \ \text{v }\!\!\mu\!\!\text{ }\,125\ V$ D. $75\Omega \ \text{v }\!\!\mu\!\!\text{ }\,125\sqrt{2}\ V$ |
Lời giải chi tiết
Ta có khi điện áp hai đầu cuộn cảm cực đại: ${{U}_{L\max }}\to \left\{ \begin{array}{} {{Z}_{L}}=\frac{{{R}^{2}}+Z_{C}^{2}}{{{Z}_{C}}}=100\Omega \\ {} {{U}_{L\max }}=\frac{U}{R}\sqrt{{{R}^{2}}+Z_{C}^{2}}=125\,V \\ \end{array} \right..$
Chọn A.
| Bài tập 2: Đặt điện áp xoay chiều $u={{U}_{0}}\cos \omega t$vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L thay đổi được và tụ điện có điện dung C. Biết rằng $\omega RC=1.$ Để điện áp hiệu dụng giữa hai đầu cuộn cảm đạt giá trị cực đại thì phải điều chỉnh L tới giá trị là:
A. $L=\frac{2}{{{\omega }^{2}}C}.$ B. $L=\frac{1}{{{\omega }^{2}}C}.$ C. $L=\frac{\sqrt{3}}{{{\omega }^{2}}C}.$ D. $L=\frac{\sqrt{2}}{{{\omega }^{2}}C}.$ |
Lời giải chi tiết
Khi điện áp hai đầu cuộn cảm cực đại thì:
${{Z}_{L}}=\frac{{{R}^{2}}+Z_{C}^{2}}{{{Z}_{C}}}=\frac{\frac{1}{{{C}^{2}}{{\omega }^{2}}}+\frac{1}{{{C}^{2}}{{\omega }^{2}}}}{\frac{1}{C\omega }}=\frac{2}{C\omega }\Rightarrow L=\frac{2}{{{\omega }^{2}}C}.$ Chọn A.
| Bài tập 3: Cho mạch điện $RLC$ mắc nối tiếp như hình vẽ, với L thay đổi được. Điện áp ở hai đầu mạch là $u=160\sqrt{2}\cos 100\pi t\left( V \right)$
$R=80\Omega ,\,C=\frac{{{10}^{-4}}}{0,8\pi }\left( F \right).$ Điều chỉnh L để điện áp hiệu dụng hai đầu cuộn cảm cực đại. Giá trị của ${{U}_{AN}}$ là: A. $80\sqrt{10}\,\text{V}.$ B. $160\sqrt{2}\,\text{V}.$ C. $160\sqrt{10}\,\text{V}.$ D. $160\,\text{V}.$ |
Lời giải chi tiết
Ta có ${{Z}_{C}}=80\,\Omega $
Thay đổi L để
${{U}_{L\max }}\to \left\{ \begin{array}{} {{Z}_{L}}=\frac{{{R}^{2}}+Z_{C}^{2}}{{{Z}_{C}}}=160\Omega \\ {} {{U}_{L\max }}=\frac{U}{R}\sqrt{{{R}^{2}}+Z_{C}^{2}}=160\sqrt{2}\,V \\ \end{array} \right.\Rightarrow I=\sqrt{2}\,A\Rightarrow {{U}_{AN}}=I.{{Z}_{RL}}=80\sqrt{10}\,V.$ Chọn A.
| Bài tập 4: Cho mạch điện xoay chiều AB gồm $R,\,L,\,C$ mắc nối tiếp. Cuộn cảm thuần có độ tự cảm thay đổi được. Đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều ổn định $u=100\sqrt{6}\cos 100\pi t\left( V \right).$ Điều chỉnh độ tự cảm để điện áp hiệu dụng hai đầu cuộn cảm đạt giá trị cực đại là ${{U}_{L\max }}$ thì điện áp hiệu dụng hai đầu tụ điện là 200 V. Giá trị ${{U}_{L\max }}$là
A. $200\,V.$ B. $150\,V.$ C. $300\,V.$ D. $250\,V.$ |
Lời giải chi tiết
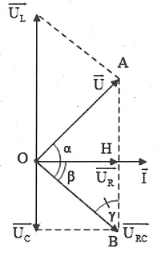
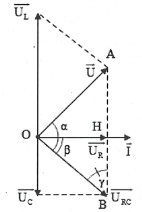
Ta có: $\cos \beta =\frac{{{U}_{R}}}{{{U}_{RC}}}=\frac{R}{\sqrt{{{R}^{2}}+Z_{C}^{2}}}.$
Áp dụng định lý hàm sin trong $\Delta OAB$ta có:
$\frac{{{U}_{L}}}{\sin \left( \alpha +\beta \right)}=\frac{U}{\sin \gamma }=\frac{U}{\cos \beta }=\frac{U\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}.$
Suy ra ${{U}_{L}}=\frac{U\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}\sin \left( \alpha +\beta \right)\le \frac{U\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}.$
Dấu bằng xảy ra $\Leftrightarrow \alpha +\beta =\frac{\pi }{2}\Leftrightarrow \overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}.$
Áp dụng hệ thức lượng trong tam giác vuông.
Ta có: $O{{A}^{2}}=AB.AH\Rightarrow {{U}^{2}}={{U}_{L}}\left( {{U}_{L}}-{{U}_{C}} \right)$
$\Leftrightarrow {{100}^{2}}.3=U_{L}^{2}-200{{U}_{L}}\Rightarrow {{U}_{L}}=300\,V.$ Chọn C.
| Bài tập 5: [Trích đề thi đại học năm 2011] Đặt điện áp xoay chiều $u=U\sqrt{2}\cos \left( 100\pi t \right)\left( V \right)$vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, tụ điện có điện dung C và cuộn cảm thuần có độ tự cảm L thay đổi được. Điều chỉnh L để điện áp hiệu dụng ở hai đầu cuộn cảm đạt giá trị cực đại thì thấy giá trị cực đại đó bằng $100\,V$và điện áp hiệu dụng ở hai đầu tụ điện bằng $36\,V$. Giá trị của U là:
A. $48\,V.$ B. $136\,V.$ C. $80\,V.$ D. $64\,V.$ |
Lời giải chi tiết
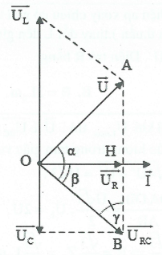
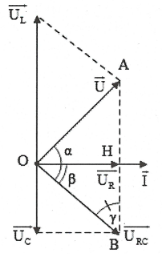
Ta có: $\cos \beta =\frac{{{U}_{R}}}{{{U}_{RC}}}=\frac{R}{\sqrt{{{R}^{2}}+Z_{C}^{2}}}$
Áp dụng định lý hàm sin trong $\Delta OAB$ ta có:
$\frac{{{U}_{L}}}{\sin \left( \alpha +\beta \right)}=\frac{U}{\sin \gamma }=\frac{U}{\cos \beta }=\frac{U\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}.$
Suy ra ${{U}_{L}}=\frac{U\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}\sin \left( \alpha +\beta \right)\le \frac{U\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}.$
Dấu bằng xảy ra $\Leftrightarrow \alpha +\beta =\frac{\pi }{2}\Leftrightarrow \overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}.$
Áp dụng hệ thức lượng trong tam giác vuông.
Ta có: $O{{A}^{2}}=AB.AH\Rightarrow {{U}^{2}}={{U}_{L}}\left( {{U}_{L}}-{{U}_{C}} \right)$
$=100.\left( 100-36 \right)\Rightarrow U=80\,\Omega .$ Chọn C.
| Bài tập 6: Đoạn mạch xoay chiều $R,L,C$có cuộn thuần cảm L có giá trị thay đổi được. Dùng ba vôn kế xoay chiều có điện trở rất lớn đo điện áp hiệu dụng trên mỗi phần tử. Điều chỉnh giá trị của L thì thấy điện áp hiệu dụng cực đại trên cuộn cảm lớn gấp hai lần điện áp hiệu dụng cực đại trên điện trở. Hỏi điện áp hiệu dụng cực đại trên cuộn cảm gấp bao nhiêu lần điện áp hiệu dụng trên tụ.
A. $\frac{4}{3}$ B. $3.$ C. $\sqrt{3}.$ D. $\frac{3}{4}.$ |
Lời giải chi tiết
Khi L thay đổi thì ${{U}_{R}}=\frac{U}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}\le \frac{U}{R}\Rightarrow {{U}_{R\max }}={{U}_{AB}}.$ Do đó ${{U}_{L\max }}=2U.$
Mặt khác khi ${{U}_{L\max }}$ thì $\overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}.$ Áp dụng hệ thức lượng ta có:
${{U}^{2}}=\left( {{U}_{L}}-{{U}_{C}} \right).{{U}_{L}}=\left( 2U-{{U}_{C}} \right).2U\Rightarrow {{U}_{C}}=\frac{3U}{2}\Rightarrow \frac{{{U}_{L}}}{{{U}_{C}}}=\frac{4}{3}.$ Chọn A.
| Bài tập 7: Đặt điện áp xoay chiều có giá trị hiệu dụng $U=30\,\text{V}$vào hai đầu đoạn mạch RLC nối tiếp. Biết cuộn dây thuần cảm, có độ cảm L thay đổi được. Khi điện áp hiệu dụng hai đầu cuộn dây đạt cực đại thì hiệu điện thế hiệu dụng hai đầu điện trở là $\text{24}\,\text{V}\text{.}$ Giá trị hiệu điện thế hiệu dụng cực đại hai đầu cuộn dây là:
A.$\text{50}\,\text{V}\text{.}$ B.$\text{40}\,\text{V}\text{.}$ C.$\text{40}\sqrt{2}\,\text{V}\text{.}$ D. $\text{16}\,\text{V}\text{.}$ |
Lời giải chi tiết
Ta có khi ${{\text{U}}_{L\max }}$ thì: $\overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}.$
Áp dụng hệ thức lượng trong tam giác vuông.
Ta có: $\frac{1}{{{U}^{2}}}+\frac{1}{U_{RC}^{2}}=\frac{1}{U_{R}^{2}}\Rightarrow {{U}_{RC}}=40\,\text{V}$
$\Rightarrow {{\text{U}}_{L}}=\sqrt{{{U}^{2}}+U_{RC}^{2}}=50\,\text{V}\text{.}$ Chọn A.
| Bài tập 8: Đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch RLC mắc nối tiếp (L là cuộn cảm thuần). Thay đổi L đến giá trị ${{\text{L}}_{0}}$ thì điện áp hiệu dụng trên cuộn dây đạt giá trị cực đại và ${{U}_{L}}=2U.$ Điện trở R bằng:
A. $R={{L}_{0}}\omega .$ B. $R=2{{L}_{0}}\omega .$ C. $R=\sqrt{3}{{L}_{0}}\omega .$ D. $R=\frac{\sqrt{3}}{4}{{L}_{0}}\omega .$ |
Lời giải chi tiết
Ta có khi ${{\text{U}}_{L\max }}$ thì $\overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}.$
Áp dụng hệ thức lượng trong tam giác vuông.
Ta có: ${{U}_{RC}}=\sqrt{4{{U}^{2}}-{{U}^{2}}}=U\sqrt{3}.$
Do đó ${{U}_{R}}=\frac{OA.OB}{AB}=\frac{U\sqrt{3}}{2},\,{{U}_{L}}=2U.$
Suy ra $\frac{{{U}_{R}}}{{{U}_{L}}}=\frac{\sqrt{3}}{4}\Rightarrow R=\frac{\sqrt{3}}{4}{{Z}_{L}}=\frac{\sqrt{3}}{4}{{L}_{0}}\omega .$ Chọn D.
| Bài tập 9: [Trích đề thi Cao đẳng năm 2009] Đặt điện áp $u={{U}_{0}}\cos \omega t$ vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, tụ điện và cuộn cảm thuần có độ tự cảm L thay đổi được. Biết dung kháng của tụ điện bằng $R\sqrt{3}$. Điều chỉnh L để điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại, khi đó:
A. Điện áp giữa hai đầu tụ điện lệch pha $\text{ }\!\!\pi\!\!\text{ /6}$ so với điện áp giữa hai đầu đoạn mạch. B. Điện áp giữa hai đầu cuộn cảm lệch pha $\text{ }\!\!\pi\!\!\text{ /6}$ so với điện áp giữa hai đầu đoạn mạch. C. Trong mạch có cộng hưởng điện. D. Điện áp giữa hai đầu điện trở lệch pha $\text{ }\!\!\pi\!\!\text{ /6}$ so với điện áp giữa hai đầu đoạn mạch. |
Lời giải chi tiết
Ta có khi ${{\text{U}}_{L\max }}$ thì $\overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}.$
Mặt khác $\tan \beta =\frac{{{Z}_{C}}}{R}=\sqrt{3}\Rightarrow \beta =\frac{\pi }{3}\Rightarrow \alpha =\frac{\pi }{6}.$ Chọn D.
| Bài tập 10: Đặt một điện áp xoay chiều ổn định $u=60\cos \omega t\left( \text{V} \right)$ vào hai đầu đoạn mạch AB gồm một điện trở, một tụ điện, một cuộn cảm thuần có độ tự cảm L thay đổi được mắc nối tiếp nhau theo đúng thứ tự. Điểm M nằm giữa tụ điện và cuộn cảm. Điều chỉnh L để có điện áp hiệu dụng hai đầu cuộn cảm đạt cực đại. Khi đó điện áp hiệu dụng hai đầu tụ điện là $30\text{ V}$. Phát biểu nào sau đây là sai?
A. Điện áp hiệu dụng hai đầu cuộn cảm là $60\text{ V}$. B. Điện áp hai đầu đoạn mạch lệch pha $\pi \text{/4}$ so với điện áp hai đầu đoạn MB. C. Điện áp hiệu dụng hai đầu điện trở là $\text{25}\sqrt{2}\,\text{V}\text{.}$ D. Điện áp hai đầu đoạn mạch vuông pha với điện áp hai đầu đoạn AM. |
Lời giải chi tiết
Ta có khi ${{\text{U}}_{L\max }}$ thì $\overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}.$
Khi đó: $U=OA=30\sqrt{2},\,HB=30.$
Mặt khác $O{{A}^{2}}=AB.HA={{U}_{L}}\left( {{U}_{L}}-30 \right)={{30}^{2}}.2$
$\Rightarrow {{U}_{L}}=60\,\text{V}=AB\Rightarrow \Delta OAB$ vuông cân tại O.
${{U}_{R}}=30\,\text{V}$ suy ra C sai. Chọn C.
| Bài tập 11: [Trích đề thi đại học năm 2009] Đặt một điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch AB gồm một cuộn cảm thuần có độ tự cảm L, điện trở thuần R và tụ điện có điện dung C mắc nối tiếp theo thứ tự trên. Gọi ${{U}_{L}},\,{{U}_{R}}$ và ${{U}_{C}}$ lần lượt là các điện áp hiệu dụng giữa hai đầu mỗi phần tử. Biết điện áp giữa hai đầu đoạn mạch AB lệch pha $\text{ }\!\!\pi\!\!\text{ /2}$ so với điện áp giữa hai đầu đoạn mạch NB (đoạn mạch NB gồm R và C). Hệ thức nào dưới đây là đúng?
A. ${{U}^{2}}=U_{R}^{2}+U_{C}^{2}+U_{L}^{2}.$ B. $U_{C}^{2}=U_{R}^{2}+U_{L}^{2}+{{U}^{2}}.$ C. $U_{L}^{2}=U_{R}^{2}+U_{C}^{2}+{{U}^{2}}.$ D. $U_{R}^{2}=U_{C}^{2}+U_{L}^{2}+{{U}^{2}}.$ |
Lời giải chi tiết
Ta có: $\overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}$$\Rightarrow {{U}^{2}}+U_{RC}^{2}=U_{L}^{2}$
$\Leftrightarrow {{U}^{2}}+U_{R}^{2}+U_{C}^{2}=U_{L}^{2}.$ Chọn C.
| Bài tập 12: Một đoạn mạch xoay chiều mắc nối tiếp gồm điện trở thuần R, tụ điện C và cuộn dây thuần cảm có độ tự cảm L thay đổi được. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều ổn định, khi điều chỉnh độ tự cảm của cuộn cảm đến giá trị ${{L}_{0}}$thì điện áp hiệu dụng hai đầu các phần tử $R,\,L,\,C$có giá trị lần lượt là 30 V, 20 V và 60 V. Khi điều chỉnh độ tự cảm đến giá trị $2{{L}_{0}}$thì điện áp hiệu dụng hai đầu điện trở bằng bao nhiêu?
A. $50\,\text{V}\text{.}$ B. $\frac{50\,}{\sqrt{3}}\text{V}\text{.}$ C. $\frac{150}{\sqrt{13}}\,\text{V}\text{.}$ D. $\frac{100}{\sqrt{11}}\,\text{V}\text{.}$ |
Lời giải chi tiết
Điện áp hiệu dụng đặt vào hai đầu đoạn mạch: $U=\sqrt{U_{R1}^{2}+{{\left( {{U}_{L1}}-{{U}_{C1}} \right)}^{2}}}=50\,\text{V}\text{.}$
Do ${{U}_{R1}}=30\,\text{V, }{{U}_{L1}}=20\text{ V, }{{U}_{C1}}=60\text{ V}\Rightarrow {{\text{Z}}_{C}}=2R;\,{{Z}_{L1}}=\frac{2R}{3}.$
Khi $L=2{{L}_{0}}\Rightarrow \left\{ \begin{array}{} {{\text{Z}}_{C}}=2R \\ {} {{Z}_{L2}}=2{{Z}_{L1}}=\frac{4R}{3} \\ \end{array} \right.\Rightarrow Z=\sqrt{{{R}^{2}}+{{\left( \frac{4R}{3}-2R \right)}^{2}}}=\frac{\sqrt{13}}{3}R.$
Do đó ${{U}_{{{R}_{2}}}}=\frac{U}{Z}.R=\frac{150}{\sqrt{13}}\,\text{V}\text{.}$ Chọn C.
|
Ví dụ 13: Cho mạch điện gồm $R,\,L,\,C$ mắc nối tiếp. Cho $R=30\Omega ,\,C=250\left( \mu F \right),$ cuộn cảm thuần có độ tự cảm L thay đổi được. Đặt vào hai đầu mạch điện một điện áp xoay chiều $u=120\cos \left( 100t+\frac{\pi }{2} \right)\left( \text{V} \right).$ Khi $L={{L}_{0}}$ thì công suất trong mạch đạt giá trị cực đại. Khi đó biểu thức điện áp giữa hai đầu cuộn cảm L là: A. ${{u}_{L}}=160\cos \left( 100t+\frac{\pi }{2} \right)\left( \text{V} \right).$ B. ${{u}_{L}}=80\sqrt{2}\cos \left( 100t+\pi \right)\left( \text{V} \right).$ C. ${{u}_{L}}=160\cos \left( 100t+\pi \right)\left( \text{V} \right).$ D. ${{u}_{L}}=80\sqrt{2}\cos \left( 100t+\frac{\pi }{2} \right)\left( \text{V} \right).$ |
Lời giải
Ta có: ${{Z}_{C}}=40\Omega ,\,P=R{{I}^{2}}=R.\frac{{{U}^{2}}}{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\frac{{{U}^{2}}}{R+\frac{{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}{R}}.$
${{P}_{\max }}\Leftrightarrow {{Z}_{L}}={{Z}_{C}}\Rightarrow Z=R=30\Omega \Rightarrow {{I}_{0}}=\frac{{{U}_{0}}}{Z}=4A,\,{{U}_{0L}}={{Z}_{L}}.{{I}_{0}}=160\text{V}$
Khi đó ${{u}_{L}}$nhanh hơn $u$góc $\frac{\pi }{2}$ nên ${{u}_{L}}=160\cos \left( 100t+\pi \right)\left( \text{V} \right).$ Chọn C.
|
Ví dụ 14: Cho mạch điện gồm $R,\,L,\,C$ mắc nối tiếp. Cho $R=50\Omega ,\,C=\frac{100}{\pi }\mu F,$ cuộn cảm thuần có độ tự cảm L thay đổi được. Đặt vào hai đầu mạch điện một điện áp xoay chiều $u=200\cos \left( 100\pi t+\frac{\pi }{2} \right)\left( \text{V} \right)$. Khi $L={{L}_{0}}$ thì công suất trong mạch đạt giá trị cực đại. Khi đó cường độ dòng điện hiệu dụng I qua mạch và điện áp giữa hai đầu điện trở R bằng bao nhiêu: A. $I=4A,\,{{U}_{R}}=200\text{V}\text{.}$ B. $I=0,8\sqrt{5}A,\,{{U}_{R}}=40\sqrt{5}\text{V}\text{.}$ C. $I=4\sqrt{10}A,\,{{U}_{R}}=20\sqrt{10}\text{V}\text{.}$ D. $I=2\sqrt{2}A,\,{{U}_{R}}=100\sqrt{2}\text{V}\text{.}$ |
Lời giải
Ta có ${{Z}_{C}}=100\,\Omega ,\,P=R{{I}^{2}}=R.\frac{{{U}^{2}}}{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\frac{{{U}^{2}}}{R+\frac{{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}{R}}.$
${{P}_{\max }}\Leftrightarrow {{Z}_{L}}={{Z}_{C}}\Rightarrow Z=R=50\Omega \Rightarrow I=\frac{U}{Z}=2\sqrt{2}A,\,U={{U}_{R}}=100\sqrt{2}\text{V}\text{.}$Chọn D.
|
Ví dụ 15: Đặt điện áp $u=U\sqrt{2}\cos \omega t\left( \text{V} \right)$vào hai đầu đoạn mạch nối tiếp gồm $R=100\Omega $, tụ điện C và cuộn cảm có độ tự cảm L thay đổi được. Khi $L={{L}_{1}}=\frac{1}{\pi }\left( H \right)$ thì cường độ dòng điện qua mạch cực đại. Khi ${{L}_{2}}=2{{L}_{1}}$ thì điện áp ở đầu cuộn cảm thuần đạt cực đại. Tần số $\omega $ bằng: A. $200\pi \,rad\text{/}s.$ B. $125\pi \,rad\text{/}s.$ C. $100\pi \,rad\text{/}s.$ D. $120\pi \,rad\text{/}s.$ |
Lời giải
Khi $L={{L}_{1}}$ thì ${{I}_{\max }}\Rightarrow $cộng hưởng điện suy ra ${{Z}_{{{L}_{1}}}}={{Z}_{C}}.$
Khi $L={{L}_{2}}=2{{L}_{1}}\Rightarrow {{Z}_{{{L}_{2}}}}=2{{Z}_{{{L}_{1}}}}$ thì ${{U}_{L\max }}\Rightarrow {{Z}_{{{L}_{2}}}}=\frac{{{R}^{2}}+Z_{C}^{2}}{{{Z}_{C}}}\Rightarrow 2{{Z}_{C}}=\frac{{{R}^{2}}+Z_{C}^{2}}{{{Z}_{C}}}$
$\Leftrightarrow R={{Z}_{C}}={{Z}_{{{L}_{1}}}}=100\ \Omega \Rightarrow \omega =100\pi \,rad\text{/}s.$ Chọn C.
|
Ví dụ 16: [Trích đề thi Chuyên ĐH Vinh lần 2-2017] Cho mạch điện như hình vẽ, biết ${{u}_{AB}}=100\sqrt{2}\cos 100\pi t\left( \text{V} \right),\,R=50\Omega ,\,C=\frac{{{10}^{-3}}}{5\sqrt{3}\pi }F,$ cuộn dây thuần cảm có độ tự cảm có thể thay đổi được. Trong quá trình thay đổi L, điện áp hiệu dụng ${{U}_{MB}}$ đạt giá trị nhỏ nhất khi: A. $\frac{2}{\sqrt{3}\pi }.\,$ B. $\frac{\sqrt{3}}{\pi }.\,$ C. $\frac{1}{2\pi }.$ D. $\frac{\sqrt{3}}{2\pi }.$ |
Lời giải
Ta có ${{Z}_{C}}=50\sqrt{3}\,\Omega ,{{U}_{MB}}=\left| {{Z}_{L}}-{{Z}_{C}} \right|.\frac{U}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{U}{\sqrt{{{\left( \frac{R}{{{Z}_{L}}-{{Z}_{C}}} \right)}^{2}}+1}}.$
Do đó ${{U}_{MB}}$ nhỏ nhất khi ${{\left( \frac{R}{{{Z}_{L}}-{{Z}_{C}}} \right)}^{2}}+1$ lớn nhất, khi đó ${{Z}_{L}}={{Z}_{C}}\Rightarrow L=\frac{\sqrt{3}}{2}\pi .$ Chọn D.
|
Ví dụ 17: [Trích đề thi Chuyên ĐH Vinh 2013] Cho mạch điện $RLC$nối tiếp, cuộn dây thuần cảm có độ tự cảm L thay đổi được. Đặt vào hai đầu đoạn mạch điện áp $u=200\sqrt{2}\cos 100\pi t\left( \text{V} \right).$ Điều chỉnh $L={{L}_{1}}$ thì điện áp hiệu dụng hai đầu cuộn dây đạt cực đại và gấp đôi điện áp hiệu dụng trên điện trở R khi đó. Sau khi điều chỉnh $L={{L}_{2}}$ để điện áp hiệu dụng trên R cực đại, thì điện áp hiệu dụng hai đầu cuộn dây là A. $100\text{ V}\text{.}$ B. $300\text{ V}\text{.}$ C. $200\text{ V}\text{.}$ D. $150\text{ V}\text{.}$ |
Lời giải
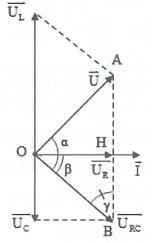
Ta có khi ${{U}_{L\max }}$ thì $\overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}$
Khi đó: $U=OA=200\text{ V,}\,{{U}_{L}}=2{{U}_{R}}.$
Suy ra $AB=2OH$nên tam giác OAB vuông cân.
Do đó ${{U}_{C}}={{U}_{R}}\Rightarrow R={{Z}_{C}}.$
Điều chỉnh L để ${{U}_{R\max }}\Leftrightarrow R={{Z}_{C}}={{Z}_{L2}}.$
Khi đó: ${{U}_{L}}=\frac{{{Z}_{L2}}.U}{R}=U=200\text{V}\text{.}$ Chọn C.
Dạng 2. Bài toán hai giá trị ${{\mathbf{L}}_{\mathbf{1}}};{{\mathbf{L}}_{\mathbf{2}}}$
a. Trường hợp 1: (Nhóm Cộng hưởng).
+) Với hai giá trị $L={{L}_{1}},L={{L}_{2}}$ làm cho một trong các đại lượng $I,P,{{U}_{R}},{{U}_{C}}$ không đổi.
+) Với $L={{L}_{0}}\to {{I}_{\max }},{{P}_{\max }},{{U}_{C\max }},{{U}_{R\max }}$ (khi xảy ra cộng hưởng).
Ta có: $.$
Chứng minh:
Xét hai giá trị $L={{L}_{1}},L={{L}_{2}}$ làm cho I không đổi.
Khi đó: ${{I}_{1}}={{I}_{2}}\Rightarrow {{Z}_{1}}={{Z}_{2}}\Leftrightarrow {{R}^{2}}+{{\left( {{Z}_{L1}}-{{Z}_{C}} \right)}^{2}}={{R}^{2}}+{{\left( {{Z}_{L2}}-{{Z}_{C}} \right)}^{2}}$
$\Leftrightarrow \left| {{Z}_{L1}}-{{Z}_{C}} \right|=\left| {{Z}_{L2}}-{{Z}_{C}} \right|\Rightarrow {{Z}_{L1}}+{{Z}_{L2}}=2{{Z}_{C}}.$
Khi $L={{L}_{0}}$ để ${{I}_{\max }}\Rightarrow {{Z}_{L0}}={{Z}_{C}}$ suy ra ${{Z}_{L1}}+{{Z}_{L2}}=2{{Z}_{L0}}\Rightarrow {{L}_{1}}+{{L}_{2}}=2{{L}_{0}}.$
Khi đó: $\frac{R}{{{Z}_{1}}}=\frac{R}{{{Z}_{2}}}\Rightarrow \cos {{\varphi }_{1}}=\cos {{\varphi }_{2}}\Rightarrow {{\varphi }_{1}}=-{{\varphi }_{2}}.$
b. Trường hợp 2: (Liên quan ${{U}_{L\max }})$
+) Với hai giá trị $L={{L}_{1}},L={{L}_{2}}$ làm cho một trong các đại lượng ${{U}_{L}}$không đổi.
+) Với $L={{L}_{0}}\to {{U}_{L\max }}$(khi ${{Z}_{L}}=\frac{{{R}^{2}}+Z_{C}^{2}}{2{{Z}_{C}}}).$
Chứng minh:
Ta có: ${{U}_{L}}={{Z}_{L}}.\frac{U}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{U}{\sqrt{\frac{{{R}^{2}}}{Z_{L}^{2}}+{{\left( 1-\frac{{{Z}_{C}}}{{{Z}_{L}}} \right)}^{2}}}}=\frac{{{U}^{2}}}{\sqrt{\frac{{{R}^{2}}+Z_{C}^{2}}{Z_{L}^{2}}-2\frac{{{Z}_{C}}}{{{Z}_{L}}}+1}}.$
Thành phần không đổi là: $\frac{{{R}^{2}}+Z_{C}^{2}}{Z_{L}^{2}}-2\frac{{{Z}_{C}}}{{{Z}_{L}}}+1=k\left( k=const=\frac{{{U}^{2}}}{U_{L}^{2}} \right).$
Do đó: $\frac{{{R}^{2}}+Z_{C}^{2}}{Z_{L}^{2}}-2\frac{{{Z}_{C}}}{{{Z}_{L}}}+1-k=0\,(*)$ (Phương trình ẩn $\frac{1}{{{Z}_{L}}}).$
Theo Viet cho (*) ta có: $\frac{1}{{{Z}_{L1}}}+\frac{1}{{{Z}_{L2}}}=\frac{-b}{a}=\frac{2{{Z}_{C}}}{{{R}^{2}}+Z_{C}^{2}}=\frac{2}{{{Z}_{L0}}}\Leftrightarrow .$
c. Ví dụ minh họa
|
Ví dụ minh họa: Cho mạch điện $RLC$ có L thay đổi được. Điện áp hai đầu mạch điện là $u=200\sqrt{2}\cos 100\pi t\,\text{V}\text{.}$ Khi mạch có $L={{L}_{1}}=\frac{3\sqrt{3}}{\pi }\,H$ và $L={{L}_{2}}=\frac{\sqrt{3}}{\pi }\,H$ thì mạch có cùng cường độ dòng điện hiệu dụng nhưng giá trị tức thời lệch pha nhau góc $2\pi \text{/3}\,rad.$ a) Tính giá trị của R và C. b) Viết biểu thức của cường độ dòng điện chạy trong mạch. |
Lời giải
Ta có ${{Z}_{L1}}=300\sqrt{3}\,\Omega ,\,{{Z}_{L2}}=100\sqrt{3}\,\Omega .$
a) Do ${{I}_{1}}={{I}_{2}}\Leftrightarrow {{Z}_{1}}={{Z}_{2}}\Leftrightarrow {{R}^{2}}+{{\left( {{Z}_{L1}}-{{Z}_{C}} \right)}^{2}}={{R}^{2}}+{{\left( {{Z}_{L2}}-{{Z}_{C}} \right)}^{2}}$
$\Leftrightarrow \left[ \begin{array}{} {{Z}_{{{L}_{1}}}}-{{Z}_{C}}={{Z}_{{{L}_{2}}}}-{{Z}_{C}} \\ {} {{Z}_{{{L}_{1}}}}-{{Z}_{C}}={{Z}_{C}}-{{Z}_{{{L}_{2}}}} \\ \end{array} \right.\Rightarrow \left[ \begin{array}{} {{Z}_{L1}}={{Z}_{L2}} \\ {} {{Z}_{C}}=\frac{{{Z}_{L1}}+{{Z}_{L2}}}{2} \\ \end{array} \right.\Rightarrow {{Z}_{C}}=\frac{{{Z}_{L1}}+{{Z}_{L2}}}{2}$
Thay số ta được ${{Z}_{C}}=\frac{{{Z}_{{{L}_{1}}}}+{{Z}_{{{L}_{2}}}}}{2}=200\sqrt{3}\,\Omega \Rightarrow C=\frac{{{10}^{-4}}}{2\sqrt{2}}F.$
Gọi ${{\varphi }_{1}}$ là độ lệch pha của u và i khi $L={{L}_{1}},\,{{\varphi }_{2}}$ là độ lệch pha của u và i khi $L={{L}_{2}}.$
Ta có $\left[ \begin{array}{} \tan {{\varphi }_{1}}=\frac{{{Z}_{{{L}_{1}}}}-{{Z}_{C}}}{R}=\frac{100\sqrt{3}}{R} \\ {} tan{{\varphi }_{1}}=\frac{{{Z}_{{{L}_{2}}}}-{{Z}_{C}}}{R}=-\frac{100\sqrt{3}}{R} \\ \end{array} \right..$ Do ${{Z}_{L2}}-{{Z}_{C}}={{Z}_{C}}-{{Z}_{L2}}\Rightarrow {{\varphi }_{1}}=-{{\varphi }_{2}}.$
Mặt khác ${{Z}_{L1}}>{{Z}_{L2}}\Rightarrow \left\{ \begin{array}{} {{\varphi }_{1}}>0 \\ {} {{\varphi }_{2}}<0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} {{\varphi }_{1}}=\frac{\pi }{3} \\ {} {{\varphi }_{2}}=-\frac{\pi }{3} \\ \end{array} \right..$
Từ đó ta được $\tan \frac{\pi }{3}=\frac{100\sqrt{3}}{R}\Rightarrow R=100\,\Omega .$
Vậy các giá trị cần tìm là $R=100\,\Omega ,\,C=\frac{{{10}^{-4}}}{2\sqrt{3}\pi }F.$
b) Viết biểu thức của i:
Với $R=100\,\Omega ,\,{{Z}_{C}}=200\sqrt{3}\,\Omega ,\,{{Z}_{L}}=300\sqrt{3}\,\Omega \Rightarrow Z=200\,\Omega \Rightarrow {{I}_{0}}=\sqrt{2}\,A.$
Độ lệch pha của u và i: $\tan {{\varphi }_{1}}=\frac{{{Z}_{L1}}-{{Z}_{C}}}{R}=\frac{100\sqrt{3}}{100}=\sqrt{3}\Rightarrow \varphi =\frac{\pi }{3}={{\varphi }_{u}}-{{\varphi }_{i}}\Rightarrow {{\varphi }_{i}}=-\frac{\pi }{3}.$
Vậy $i=\sqrt{2}\cos \left( 100\pi t-\frac{\pi }{3} \right)A.$
Với $R=100\,\Omega ,\,{{Z}_{C}}=200\sqrt{3}\,\Omega ,\,{{Z}_{L}}=100\sqrt{3}\,\Omega \Rightarrow Z=200\,\Omega .$
Ta có $tan{{\varphi }_{2}}=\frac{{{Z}_{{{L}_{2}}}}-{{Z}_{C}}}{R}=-\frac{100\sqrt{3}}{100}=-\sqrt{3}\Rightarrow \varphi =-\frac{\pi }{3}={{\varphi }_{u}}-{{\varphi }_{i}}\Rightarrow {{\varphi }_{i}}=\frac{\pi }{3}.$
Vậy $i=\sqrt{2}\cos \left( 100\pi t+\frac{\pi }{3} \right)\text{A}.$
d. Bài tập luyện tập dạng 2
|
Ví dụ 1: Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số 50 Hz vào hai đầu đoạn mạch mắc nối tiếp gồm: điện trở thuần R, tụ điện có điện dung C và cuộn cảm thuần có thay đổi được. Điều chỉnh độ tự cảm L đến giá trị 0,5 H hoặc 0,9 H thì điện áp hiệu dụng hai đầu điện trở R đều có giá trị bằng nhau. Giá trị của C bằng: A. $14,47\mu F.$ B. $28,95\mu F.$ C. $9,65\mu F.$ D. $48,24\mu F.$ |
Lời giải
${{Z}_{C}}=\frac{{{Z}_{{{L}_{1}}}}+{{Z}_{{{L}_{2}}}}}{2}\Rightarrow C=\frac{1}{\omega {{Z}_{C}}}=14,47\mu F.$ Chọn A.
|
Ví dụ 2: [Trích đề thi Cao đẳng năm 2012] Đặt điện áp $u={{U}_{0}}\cos \left( \omega t+\varphi \right)\,({{U}_{0}}$và $\varphi $ không đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần, tụ điện và cuộn cảm thuần có độ tự cảm L thay đổi được. Khi $L={{L}_{1}}$ hoặc $L={{L}_{2}}$ thì cường độ dòng điện hiệu dụng trong đoạn mặt bằng nhau. Để cường độ dòng điện hiệu dụng trong đoạn mạch giá trị cực đại thì giá trị của L bằng: A. $\frac{{{L}_{1}}+{{L}_{2}}}{2}.$ B. $\frac{{{L}_{1}}{{L}_{2}}}{{{L}_{1}}+{{L}_{2}}}.$ C. $\frac{2{{L}_{1}}{{L}_{2}}}{{{L}_{1}}+{{L}_{2}}}.$ D. $2\left( {{L}_{1}}+{{L}_{2}} \right).$ |
Lời giải
Xét hai giá trị $L={{L}_{1}},\,L={{L}_{2}}$ làm cho I không đổi.
Khi đó: ${{I}_{1}}={{I}_{2}}\Rightarrow {{Z}_{1}}={{Z}_{2}}\Leftrightarrow {{R}^{2}}+{{\left( {{Z}_{L1}}-{{Z}_{C}} \right)}^{2}}={{R}^{2}}+{{\left( {{Z}_{L2}}-{{Z}_{C}} \right)}^{2}}$
$\Leftrightarrow \left| {{Z}_{L1}}-{{Z}_{C}} \right|=\left| {{Z}_{L2}}-{{Z}_{C}} \right|\Rightarrow {{Z}_{L1}}+{{Z}_{L2}}=2{{Z}_{C}}.$
Khi $L={{L}_{0}}$ để ${{I}_{\max }}\Rightarrow {{Z}_{L0}}={{Z}_{C}}$ suy ra ${{Z}_{L1}}+{{Z}_{L2}}=2{{Z}_{L0}}\Rightarrow {{L}_{1}}+{{L}_{2}}=2{{L}_{0}}.$ Chọn A.
|
Ví dụ 3: Đặt điện áp xoay chiều $u={{U}_{0}}\cos 100\pi t\left( \text{V} \right)\,({{U}_{0}}$ không đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, tụ điện có điện dung $C=\frac{100}{\pi }\mu F$ và cuộn dây thuần cảm có độ tự cảm L thay đổi. Nếu $L={{L}_{1}}$ hoặc $L={{L}_{2}}=4{{L}_{1}}$ thì cường độ dòng điện hiệu dụng qua mạch như nhau. Trị số ${{L}_{1}}$ là: A. $\text{2/ }\!\!\pi\!\!\text{ }\,\text{H}\text{.}$ B. $\text{1/ }\!\!\pi\!\!\text{ }\,\text{H}\text{.}$ C. $\text{0,5/ }\!\!\pi\!\!\text{ }\,\text{H}\text{.}$ D. $\text{0,4/ }\!\!\pi\!\!\text{ }\,\text{H}\text{.}$ |
Lời giải
L thay đổi để ${{I}_{1}}={{I}_{2}}\Rightarrow {{Z}_{L1}}+{{Z}_{L2}}=2{{Z}_{C}}=200\,\Omega .$
Mặt khác ${{L}_{2}}=4{{L}_{1}}\Rightarrow {{Z}_{L2}}=4{{Z}_{L1}}\Rightarrow 5{{Z}_{L1}}=200\Rightarrow {{Z}_{L1}}=40\,\Omega \Rightarrow {{L}_{1}}=\frac{0,4}{\pi }H.$ Chọn D.
|
Ví dụ 4: Đặt điện áp xoay chiều $u={{U}_{0}}\cos 100\pi t\left( \text{V} \right)\,({{U}_{0}}$ không đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, tụ điện có điện dung $C=\frac{50}{\pi }\mu F$ và cuộn dây thuần cảm có độ tự cảm L thay đổi. Điều chỉnh L đến các giá trị lần lượt là $L={{L}_{1}}$ và $L={{L}_{2}}$ thì cường độ dòng điện hiệu dụng qua mạch như nhau. Điện áp hiệu dụng ở hai đầu cuộn cảm khi $L={{L}_{1}}$ gấp ba lần khi $L={{L}_{2}}.$ Giá trị ${{L}_{1}}$ bằng: A. $\text{3/ }\!\!\pi\!\!\text{ }\,\text{H}\text{.}$ B. $\text{1/ }\!\!\pi\!\!\text{ }\,\text{H}\text{.}$ C. $\text{2/ }\!\!\pi\!\!\text{ }\,\text{H}\text{.}$ D. $\text{0,5/ }\!\!\pi\!\!\text{ }\,\text{H}\text{.}$ |
Lời giải
L thay đổi để ${{I}_{1}}={{I}_{2}}\Rightarrow {{Z}_{L1}}+{{Z}_{L2}}=2{{Z}_{C}}=400\,\Omega .$
Lại có: ${{U}_{L1}}=3{{U}_{L2}}\Rightarrow \frac{U}{I}.{{Z}_{L1}}=3\frac{U}{I}{{Z}_{L2}}\Rightarrow {{Z}_{L1}}=3{{Z}_{L2}}\Rightarrow {{Z}_{L1}}=300\,\Omega \Rightarrow {{L}_{1}}=\frac{3}{\pi }H.$ Chọn A.
|
Ví dụ 5: Cho mạch điện $RCL$ mắc nối tiếp theo thứ tự $R,\,C,\,L$ trong đó cuộn dây thuần cảm có độ tự cảm L thay đổi được $R=100\,\Omega $. Đặt vào hai đầu đoạn mạch hiệu điện thế xoay chiều tần số $f=50\,Hz.$ Thay đổi L người ta thấy khi $L={{L}_{1}}$ và khi $L={{L}_{2}}=\frac{{{L}_{1}}}{2}$ thì công suất tiêu thụ trên đoạn mạch như nhau nhưng cường độ dòng điện tức thời vuông pha nhau. Giá trị của ${{L}_{1}}$ và điện dung của C lần lượt là: A. ${{L}_{1}}=\frac{4}{\pi }\left( H \right),\,C=\frac{{{3.10}^{-4}}}{\pi }\left( F \right).$ B. ${{L}_{1}}=\frac{4}{\pi }\left( H \right),\,C=\frac{{{10}^{-4}}}{3\pi }\left( F \right).$ C.${{L}_{1}}=\frac{2}{\pi }\left( H \right),\,C=\frac{{{10}^{-4}}}{3\pi }\left( F \right).$ D. ${{L}_{1}}=\frac{1}{4\pi }\left( H \right),\,C=\frac{{{3.10}^{-4}}}{\pi }\left( F \right).$ |
Lời giải
Xét hai giá trị $L={{L}_{1}},\,L={{L}_{2}}$ làm cho P không đổi.
Khi đó: ${{P}_{1}}={{P}_{2}}\Rightarrow {{I}_{1}}={{I}_{2}}\Rightarrow {{Z}_{1}}={{Z}_{2}}\Leftrightarrow {{R}^{2}}+{{\left( {{Z}_{L2}}-{{Z}_{C}} \right)}^{2}}={{R}^{2}}+{{\left( {{Z}_{L2}}-{{Z}_{C}} \right)}^{2}}$
$\Leftrightarrow \left| {{Z}_{L1}}-{{Z}_{C}} \right|=\left| {{Z}_{L2}}-{{Z}_{C}} \right|\Rightarrow {{Z}_{L1}}+{{Z}_{L2}}=2{{Z}_{C}}\Rightarrow \left\{ \begin{array}{} {{Z}_{L1}}=\frac{4}{3}{{Z}_{C}} \\ {} {{Z}_{L2}}=\frac{2}{3}{{Z}_{C}} \\ \end{array} \right.\left( \text{Do}\,{{Z}_{L1}}=2{{Z}_{L2}} \right).$
Theo giả thiết ta có: $\tan {{\varphi }_{1}}.\tan {{\varphi }_{2}}=-1.$
Do đó $\frac{{{Z}_{L1}}-{{Z}_{C}}}{R}.\frac{{{Z}_{L2}}-{{Z}_{C}}}{R}=-1\Rightarrow \frac{1}{9}Z_{C}^{2}={{R}^{2}}\Rightarrow {{Z}_{C}}=300\,\Omega ,\,{{Z}_{L1}}=400\,\Omega .$
Suy ra ${{L}_{1}}=\frac{4}{\pi }\left( H \right),\,C=\frac{{{10}^{-4}}}{3\pi }\left( F \right).$ Chọn B.
|
Ví dụ 6: [Trích đề thi Đại học năm 2014] Đặt điện áp $u=180\sqrt{2}\cos \omega t\left( \text{V} \right).$ (với $\omega $ không đổi) vào hai đầu đoạn mạch AB (hình vẽ). R là điện trở thuần, tụ điện có điện dung C, cuộn cảm thuần có độ tự cảm L thay đổi được. Điện áp hiệu dụng ở hai đầu đoạn mạch MB và độ lớn góc lệch pha của cường độ dòng điện so với điện áp u khi $L={{L}_{1}}$ là U và ${{\varphi }_{1}}$, còn khi $L={{L}_{2}}$ thì tương ứng là $\sqrt{8}U$ và ${{\varphi }_{2}}$. Biết ${{\varphi }_{1}}+{{\varphi }_{2}}=90{}^\circ .$ Giá trị U bằng: A. 60 V B. 180 V C. 90 V D. 135 V |
Lời giải
Cách 1: [Đại số]. Ta có: ${{U}_{MB}}=\frac{{{U}_{AB}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}\left| {{Z}_{L}}-{{Z}_{C}} \right|.$
$\Leftrightarrow {{U}_{MB}}=\frac{{{U}_{AB}}}{\sqrt{{{\left( \frac{R}{{{Z}_{L}}-{{Z}_{C}}} \right)}^{2}}+1}}=\frac{{{U}_{AB}}}{\sqrt{\frac{1}{{{\tan }^{2}}\varphi }+1}}={{U}_{AB}}\sin \varphi $ ( với $\varphi $ là độ lớn góc lệch pha).
Suy ra: $\left\{ \begin{array}{} U={{U}_{AB}}\sin {{\varphi }_{1}} \\ {} U\sqrt{8}={{U}_{AB}}\sin {{\varphi }_{2}} \\ \end{array} \right.\xrightarrow{{{\varphi }_{1}}+{{\varphi }_{2}}=\frac{\pi }{2}}{{\sin }^{2}}{{\varphi }_{1}}+{{\sin }^{2}}{{\varphi }_{2}}=1.$
$\Leftrightarrow {{\left( \frac{U}{{{U}_{AB}}} \right)}^{2}}+{{\left( \frac{U\sqrt{8}}{{{U}_{AB}}} \right)}^{2}}=1\Rightarrow U=\frac{{{U}_{AB}}}{3}=60\,\text{V}\text{.}$ Chọn A.
Cách 2: Sử dụng giãn đồ vecto:
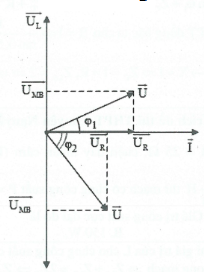
Ta có: $\sin {{\varphi }_{1}}=\frac{{{U}_{MB1}}}{{{U}_{AB}}}=\frac{U}{{{U}_{AB}}}.$
$\sin {{\varphi }_{2}}=\frac{{{U}_{MB2}}}{{{U}_{AB}}}=\frac{U\sqrt{8}}{{{U}_{AB}}}.$
Mặt khác ${{\varphi }_{1}}+{{\varphi }_{2}}=90{}^\circ $ nên:
$\Leftrightarrow {{\left( \frac{U}{{{U}_{AB}}} \right)}^{2}}+{{\left( \frac{U\sqrt{8}}{{{U}_{AB}}} \right)}^{2}}=1\Rightarrow U=\frac{{{U}_{AB}}}{3}=60\,\text{V}\text{.}$
|
Ví dụ 7: Đặt điện áp xoay chiều $u={{U}_{0}}\cos \omega t$ (với ${{U}_{0}},\,\omega $ không đổi) vào hai đầu đoạn mạch RLC, trong đó cuộn dây thuần cảm có độ tự cảm L thay đổi. Khi $L={{L}_{1}}$ hay $L={{L}_{2}}$ với ${{L}_{1}}>{{L}_{2}}$ thì công suất tiêu thụ của mạch điện tương ứng ${{P}_{1}},\,{{P}_{2}}$ với ${{P}_{1}}=3{{P}_{2}}$ độ lệch pha giữa điện áp hai đầu mạch điện với cường độ dòng điện trong mạch tương ứng ${{\varphi }_{1}};{{\varphi }_{2}}$ với $\left| {{\varphi }_{1}} \right|+\left| {{\varphi }_{2}} \right|=\frac{\pi }{2}.$ Độ lớn của ${{\varphi }_{1}}$ và ${{\varphi }_{2}}$ là: A. $\frac{\pi }{3};\,\frac{\pi }{6}.$ B. $\frac{\pi }{6};\,\frac{\pi }{3}.$ C. $\frac{5\pi }{12};\,\frac{\pi }{12}.$ D. $\frac{\pi }{12};\,\frac{5\pi }{12}.$ |
Lời giải
Ta có: ${{P}_{1}}=3{{P}_{2}}\Rightarrow \frac{{{P}_{1}}}{{{P}_{2}}}=\frac{RI_{1}^{2}}{RI_{2}^{2}}=3\Rightarrow \frac{{{I}_{1}}}{{{I}_{2}}}=\sqrt{3}.$
Mặt khác $\frac{{{P}_{1}}}{{{P}_{2}}}=\frac{U{{I}_{1}}\cos {{\varphi }_{1}}}{U{{I}_{2}}\cos {{\varphi }_{2}}}=\sqrt{3}\frac{\cos {{\varphi }_{1}}}{\cos {{\varphi }_{2}}}=3\Rightarrow \frac{\cos {{\varphi }_{1}}}{\cos {{\varphi }_{2}}}=\sqrt{3}=\frac{\cos \left| {{\varphi }_{1}} \right|}{\cos \left| {{\varphi }_{2}} \right|}.$
Kết hợp $\left| {{\varphi }_{1}} \right|+\left| {{\varphi }_{2}} \right|=\frac{\pi }{2}\Rightarrow \left\{ \begin{array}{} \left| {{\varphi }_{1}} \right|=\frac{\pi }{6} \\ {} \left| {{\varphi }_{2}} \right|=\frac{\pi }{3} \\ \end{array} \right..$ Chọn B.
|
Ví dụ 8: [Trích đề thi Đại học năm 2013] Đặt điện áp $u={{U}_{0}}\cos \omega t\,({{U}_{0}}$ và $\omega $ không đổi) vào hai đầu đoạn mạch mắc nối tiếp có điện trở R, tụ điện có điện dung C, cuộn cảm thuần có độ tự cảm L thay đổi được. Khi $L={{L}_{1}}$ và $L={{L}_{2}}$; điện áp hiệu dụng ở hai đầu cuộn cảm có cùng giá trị; độ lệch pha của điện áp ở hai đầu đoạn mạch so với cường độ dòng điện lần lượt là 0,52 rad và 1,05 rad. Khi $L={{L}_{0}}$; điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại; độ lệch pha của điện áp ở hai đầu đoạn mạch so với cường độ dòng điện là $\varphi .$ Giá trị của $\varphi $ gần giá trị nào nhất sau đây? A. $1,57\,\text{rad}\text{.}$ B. $0,83\,\text{rad}\text{.}$ C. $0,26\,\text{rad}\text{.}$ D. $0,41\,\text{rad}\text{.}$ |
Lời giải
Ta có: $\frac{1}{{{Z}_{L1}}}+\frac{1}{{{Z}_{L2}}}=\frac{2}{{{Z}_{L0}}}.$ Trong đó ${{Z}_{L0}}=\frac{Z_{C}^{2}+{{R}^{2}}}{{{Z}_{C}}}.$
Mặt khác $\tan {{\varphi }_{1}}=\frac{{{Z}_{L2}}-{{Z}_{C}}}{R}\Rightarrow {{Z}_{L2}}=R\tan {{\varphi }_{1}}+{{Z}_{C}},\,{{Z}_{L2}}=R\tan {{\varphi }_{2}}+{{Z}_{C}}.$
Suy ra $\frac{1}{R\tan {{\varphi }_{1}}+{{Z}_{C}}}+\frac{1}{R\tan {{\varphi }_{2}}+{{Z}_{C}}}=\frac{2{{Z}_{C}}}{Z_{C}^{2}+{{R}^{2}}}.$
Đây là một PT đồng bậc ta cho $R=1\Rightarrow \frac{1}{\tan 0,52+X}+\frac{1}{\tan 1,05+X}=\frac{2X}{{{X}^{2}}+1}\left( X={{Z}_{C}} \right).$
$\xrightarrow{SHIFT-CALC}X\approx 1\Rightarrow {{Z}_{C}}=1=R,\,{{Z}_{L0}}=2\Rightarrow \tan \varphi =1\Rightarrow \varphi =\frac{\pi }{4}.$ Chọn B.
|
Ví dụ 9: [Trích đề thi THPT Chuyên Nguyễn Trãi] Đặt điện áp $u={{U}_{0}}\cos 100\pi t\,\,\left( \text{V} \right)$ vào mạch điện gồm $R=25\,\Omega ;$ cuộn dây thuần cảm (L thay đổi được) và tụ điện. Khi $L={{L}_{1}}=\frac{1}{\pi }H$ và $L={{L}_{2}}=\frac{1}{2\pi }H$ thì mạch có cùng công suất $P=100\,\text{W}.$ Điều chỉnh L để công suất tiêu thụ của mạch đạt cực đại. Giá trị công suất cực đại đó là A. $100\,\text{W}.$ B. $150\,\text{W}.$ C. $175\,\text{W}.$ D. $200\,\text{W}.$ |
Lời giải
Hai giá trị của L cho cùng công suất của mạch tương đương với hai giá trị của L cho cùng dòng điện trong mạch $\Rightarrow {{Z}_{L1}}+{{Z}_{L2}}=2{{Z}_{C}}\Rightarrow {{Z}_{C}}=75\,\Omega .$
Công suất của mạch khi đó: $P=\frac{{{U}^{2}}R}{{{R}^{2}}+{{\left( {{Z}_{L1}}-{{Z}_{C}} \right)}^{2}}}=\frac{{{U}^{2}}.25}{{{25}^{2}}+{{\left( 50-75 \right)}^{2}}}=\frac{{{U}^{2}}}{50}.$
Công suất của mạch khi cực đại (cộng hưởng) ${{P}_{\max }}=\frac{{{U}^{2}}}{{{R}^{2}}}=\frac{{{U}^{2}}}{25}\Rightarrow {{P}_{\max }}=2P=200W.$ Chọn D.