CÁCH GIẢI CÁC DẠNG BÀI VỊ TRÍ CÁC ĐIỂM CỰC ĐẠI, CỰC TIỂU
Dạng 1: Vị trí các điểm dao động cực đại, cực tiểu trên AB.
Bài toán:
Tìm vị trí điểm M thuộc khoảng AB sao cho M gần ( hoặc xa ): A, B, hoặc I… nhất.
Phương pháp giải:
Đặt MB = x. Ta có: ${{d}_{2}}-{{d}_{1}}=MB-MA=x-\left( AB-x \right)=2x-AB=f\left( k \right)$
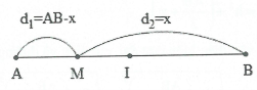
Suy ra $x=\frac{AB+f\left( k \right)}{2}$
Biện luận MB = x.
- TH1: Giải M gần B nhất: Cho $x=0\left( k\in \mathbb{Z} \right)$ tìm ${{x}_{\min }}>0.$
- TH2: Giải M gần A nhất (xa B nhất): Cho $x=AB\left( k\in \mathbb{Z} \right)$ tìm ${{x}_{\max }}<AB$.
- TH3: Giải M xa I nhất tương đương với M gần A hoặc gần B nhất.
- TH4: M gần I nhất: Cho $x=\frac{AB}{2}$ tìm $k\in \mathbb{Z}$.
Trong trường hợp này nếu M gần I nhất thuộc đoạn IB thì ta lấy giá trị $x<\frac{AB}{2}$.
Nếu M gần I nhất thuộc đoạn IA thì ta lấy giá trị $x>\frac{AB}{2}.$
Dạng 2: Vị trí các điểm cực đại cực tiểu trên đường thẳng vuông góc với AB
Phương pháp giải:
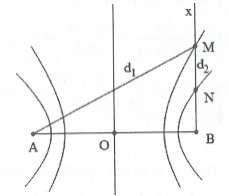
+) Đường (H) gần O nhất cắt Bx tại điểm xa B nhất.
+) Đường (H) gần B nhất cắt Bx tại điểm gần B nhất.
Tìm vị trí các điểm trên BO gần B hay xa B.
Tìm ${{d}_{2}}-{{d}_{1}}=f\left( k \right)$.
Tính ${{d}_{2}}-{{d}_{1}}$ tại B suy ra ${{k}_{B}}$.
Tính ${{d}_{2}}-{{d}_{1}}$ tại O suy ra ${{k}_{O}}$ từ đó suy ra ${{k}_{M}}$ và ${{k}_{N}}$.
Khi đó ta tính được ${{d}_{2}}-{{d}_{1}}=a$.
Giải hệ: $\left\{ \begin{array}{} {{d}_{2}}-{{d}_{1}}=a \\ {} d_{1}^{2}=d_{2}^{2}+A{{B}^{2}} \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} {{d}_{2}}-{{d}_{1}}=a \\ {} \left( {{d}_{1}}-{{d}_{2}} \right)({{d}_{1}}+{{d}_{2}})=A{{B}^{2}} \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} {{d}_{2}}-{{d}_{1}}=d \\ {} {{d}_{2}}+{{d}_{1}}=\frac{A{{B}^{2}}}{a} \\ \end{array} \right.\Rightarrow {{d}_{1}};{{d}_{2}}.$
Hoặc giải PT: ${{d}_{2}}-\sqrt{d_{2}^{2}+A{{B}^{2}}}=a\Rightarrow {{d}_{2}}$.
Dạng 3: Vị trí cực đại cực tiểu trên đường $\Delta $ song song với AB.
Xác định đường Hypebol qua M, cắt $\Delta $. Đặt
OH = CM = x. Ta có:
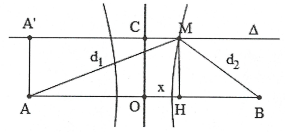
$\left\{ \begin{array}{} d_{2}^{2}={{h}^{2}}+{{\left( \frac{AB}{2}-x \right)}^{2}} \\ {} d_{1}^{2}={{h}^{2}}+{{\left( \frac{AB}{2}+x \right)}^{2}} \\ \end{array} \right.\left( h=OC \right)$
Dựa vào điều kiện cực đại, cực tiểu và đường Hypebol ta có: ${{d}_{1}}-{{d}_{2}}=f\left( k \right)=a$ (xác định).
Khi đó $\sqrt{{{h}^{2}}+{{\left( \frac{AB}{2}-x \right)}^{2}}}-\sqrt{{{h}^{2}}+{{\left( \frac{AB}{2}+x \right)}^{2}}}=a\xrightarrow{SHIFT-CALC}x=?.$
Chú ý:
+) M gần trung trực của AB nhất suy ra M thuộc Hypebol gần trung trực AB nhất.
+) M xa A nhất suy ra M thuộc Hypebol gần B nhất.
+) M gần A nhất suy ra M gần ${A}’$ nhất (hình vẽ) suy ra ${{k}_{{{A}’}}}\Rightarrow {{k}_{M}}.$
Dạng 4: Vị trí cực đại, cực tiểu trên đường tròn (C) đường kính AB.
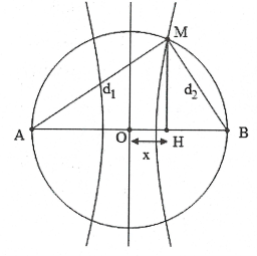
Từ giả thiết ta xác định đường Hypebol qua điểm M.
Khi đó ${{d}_{1}}-{{d}_{2}}=f\left( k \right)=a$ (đã xác định).
Suy ra ${{d}_{1}}{{d}_{2}}=\frac{d_{1}^{2}+d_{2}^{2}-{{a}^{2}}}{2}$
Lại có: $d_{1}^{2}+d_{2}^{2}=A{{B}^{2}}$ nên:
$MH=\frac{{{d}_{1}}{{d}_{2}}}{\sqrt{d_{1}^{2}+d_{2}^{2}}}=\frac{A{{B}^{2}}-{{a}^{2}}}{2AB}\Rightarrow {{d}_{1}};{{d}_{2}};x…$.
Hoặc giải hệ: $\left\{ \begin{array}{} d_{1}^{2}+d_{2}^{2}=A{{B}^{2}} \\ {} {{d}_{1}}-{{d}_{2}}=a \\ \end{array} \right.\Rightarrow {{d}_{1}};{{d}_{2}}…$
Dạng 5: Vị trí cực đại, cực tiểu trên đường tròn (C) tâm A, bán kính AB.
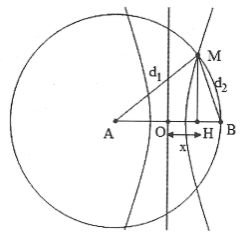
Xét điểm $M\in \left( C \right)$ tâm A bán kính R = AB.
Từ giả thiết suy ra ${{d}_{2}}-{{d}_{1}}=f\left( k \right)=a$.
Đặt OH = x ta có: $\left\{ \begin{array}{} {{d}_{2}}-{{d}_{1}}=a \\ {} {{d}_{1}}=AB \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{} {{d}_{1}} \\ {} {{d}_{2}} \\ \end{array} \right..$
$M{{H}^{2}}=d_{1}^{2}-{{\left( \frac{AB}{2}+x \right)}^{2}}=d_{2}^{2}-{{\left( \frac{AB}{2}-x \right)}^{2}}$
Giải phương trình trên tìm x.
