BÀI TẬP XÁC ĐỊNH VỊ TRÍ CĐ, CT CÓ ĐÁP ÁN CHI TIẾT
| Bài tập 1: Hai nguồn sóng kết hợp A và B dao động ngược pha, có AB = 20 cm; bước sóng $\lambda =1,5$cm. Điểm dao động với biên độ cực tiểu trên AB cách trung điểm của AB một khoảng nhỏ nhất bằng:
A. 0,25 cm. B. 0,5 cm. C. 1,5 cm. D. 0,75 cm. |
Lời giải chi tiết
Hai nguồn ngược pha, điểm M dao động với biên độ cực tiểu khi ${{d}_{2}}-{{d}_{1}}=k\lambda $
Điểm gần trung điểm của AB nhất thuộc Hypebol bậc một với $k=\pm 1$.
Khi đó: $\left\{ \begin{array}{} {{d}_{1}}+{{d}_{2}}=20 \\ {} {{d}_{1}}-{{d}_{2}}=1,5 \\ \end{array} \right.\Rightarrow {{d}_{1}}=10,75\Rightarrow x={{d}_{1}}-\frac{AB}{2}=0,75$cm. Chọn D.
| Bài tập 2: Hai nguồn sóng kết hợp A và B dao động cùng pha nhau cách nhau 24 cm với tần số f = 40 Hz. Vận tốc truyền sóng là v = 0,8 m/s. Điểm dao động với biên độ cực tiểu trên AB cách A một khoảng lớn nhất bằng:
A. 23,75 cm. B. 22,5 cm. C. 23 cm. D. 23,5 cm. |
Lời giải chi tiết
Điểm M dao động với biên độ cực tiểu khi ${{d}_{2}}-{{d}_{1}}=\left( k+0,5 \right)\lambda ;\lambda =\frac{v}{f}=2$cm
Đặt $MA=x\Rightarrow MB=24-x\Rightarrow 0<x<24$ khi đó ${{d}_{2}}-{{d}_{1}}=2x-24$
Khi đó $\left( k+0,5 \right)\lambda =2x-24\Leftrightarrow 2\left( k+0,5 \right)=2x-24\Leftrightarrow 2k+25=2x.$
Do $x<24\Rightarrow 2k+25<2.24\Rightarrow k\le 11,5\Rightarrow \left\{ \begin{array}{} {{k}_{\max }}=11 \\ {} {{x}_{\max }}=23,5\,cm \\ \end{array} \right..$ Chọn D.
| Bài tập 3: Hai nguồn sóng kết hợp A và B dao động cùng pha cùng tần số f = 50 Hz, vận tốc truyền sóng v = 40 cm/s và AB = 26,5 cm. Điểm dao động với biên độ cực tiểu trên AB cách B một khoảng gần nhất bằng:
A. 0,5 cm. B. 0,25 cm. C. 0,375 cm. D. 0,625 cm. |
Lời giải chi tiết
Điểm M dao động với biên độ cực tiểu khi ${{d}_{2}}-{{d}_{1}}=\left( k+0,5 \right)\lambda ;\lambda =\frac{v}{f}=0,8$cm
Đặt $MB=x\Rightarrow MA=26,5-x$ khi đó ${{d}_{2}}-{{d}_{1}}=2x-26,5$(với $0<x<26,5$)
Khi đó $\left( k+0,5 \right)\lambda =2x-26,5\Leftrightarrow \left( k+0,5 \right)0,8=2x-26,5\Leftrightarrow 0,8k+26,9=2x\left( k\in \mathbb{Z} \right).$
Ta có: $0,8k+26,9>0\Rightarrow k<-33,625\Rightarrow k=-33.$
$\Rightarrow {{x}_{\min }}=0,25$cm khi $k=-33$. Chọn B.
| Bài tập 4: Hai nguồn sóng kết hợp ${{S}_{1}}$ và ${{S}_{2}}$ cách nhau 2 m dao động điều hòa cùng pha, phát ra hai sóng có bước sóng 1 m. Một điểm A nằm ở khoảng cách $\ell $ kể từ ${{S}_{1}}$ và $A{{S}_{1}}\bot {{S}_{1}}{{S}_{2}}$. Giá trị cực đại của $\ell $ để tại A có được cực đại của giao thoa là:
A. $\ell =1,5$m. B. $\ell =2,0$m. C. $\ell =3,75$m. D. $\ell =2,25$m. |
Lời giải chi tiết
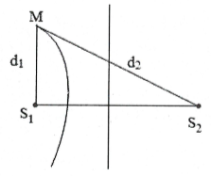
Điều kiện để tại A có cực đại giao thoa là hiệu đường đi
từ A đến hai nguồn sóng phải bằng số nguyên lần bước
sóng ( hình bên ).
${{d}_{1}}-{{d}_{2}}=\sqrt{{{\ell }^{2}}+{{d}^{2}}}-\ell =k\lambda $ (với d = 2 m)
Khi $\ell $ càng lớn thì hypebol càng gần trung trực AB.
Vậy để giá trị của $\ell $ cực đại thì hypebol gần trung trực
của AB nhất ứng với k = 1.
Khi đó: $\sqrt{{{\ell }^{2}}+4}-\ell =1\Rightarrow {{\ell }^{2}}+4={{\left( \ell +1 \right)}^{2}}\Rightarrow \ell =1,5$m.
Chọn A.
| Bài tập 5: Hai nguồn sóng kết hợp ${{S}_{1}}$ và ${{S}_{2}}$ cách nhau 8 cm dao động điều hòa cùng pha, phát ra hai sóng có bước sóng $\lambda =4$cm. Một điểm A nằm ở khoảng cách $\ell $ kể từ ${{S}_{1}}$ và $A{{S}_{1}}\bot {{S}_{1}}{{S}_{2}}$. Giá trị cực đại của $\ell $ để tại A có được cực tiểu của giao thoa là:
A. $\ell =10$cm. B. $\ell =12$cm. C. $\ell =14$cm. D. $\ell =15$cm. |
Lời giải chi tiết
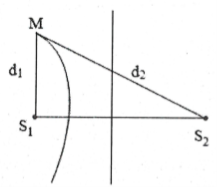
Điều kiện để tại A có cực tiểu giao thoa là:
${{d}_{1}}-{{d}_{2}}=\sqrt{{{\ell }^{2}}+{{d}^{2}}}-\ell =\left( k+0,5 \right)\lambda $
${{\ell }_{\max }}\Leftrightarrow $ dãy cực tiểu gần trung trực của AB nhất ứng
với $k=0\Rightarrow \sqrt{{{\ell }^{2}}+{{d}^{2}}}-\ell =0,5\lambda =2.$
$\Leftrightarrow \sqrt{{{\ell }^{2}}+64}={{\left( \ell +2 \right)}^{2}}\Rightarrow \ell =15$cm. Chọn D.
| Bài tập 6: Trên bề mặt chất lỏng có hai nguồn kết hợp AB cách nhau 90 cm dao động cùng pha. Biết sóng do mỗi nguồn phát ra có tần số f = 8 Hz, vận tốc truyền sóng 1,6 m/s. Gọi M là một điểm nằm trên đường vuông góc với AB tại đó A dao động với biên độ cực đại. Đoạn AM có giá trị nhỏ nhất là:
A. 10,24 cm. B. 90,6 cm. C. 22,5 cm. D. 10,625 cm. |
Lời giải chi tiết
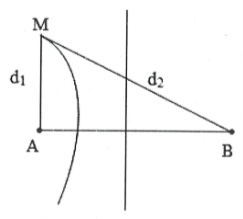
Ta có $\lambda =\frac{v}{f}=20$cm. Số vân dao động với biên độ
dao động cực đại trên đoạn AB thỏa mãn điều kiện:
$-AB\le k\lambda \le AB.$
Hay: $\frac{-AB}{\lambda }\le k\le \frac{AB}{\lambda }\Leftrightarrow -4,5\le k\le 4,5$
$\Leftrightarrow -4\le k\le 4\left( k\in \mathbb{N} \right)$
Đoạn AM có giá trị bé nhất thì M phải nằm trên đường
cực đại bậc 4 (cực đại xa trung trực AB nhất). Khi đó
${{d}_{2}}-{{d}_{1}}=4\lambda =80$cm.
Mặt khác, do tam giác AMB là tam giác vuông tại A nên ta có:
${{d}_{2}}=BM=\sqrt{A{{M}^{2}}+A{{B}^{2}}}=\sqrt{d_{1}^{2}+{{90}^{2}}}$
Suy ra $\sqrt{d_{1}^{2}+{{90}^{2}}}-{{d}_{1}}=80\,cm\,\Leftrightarrow d_{1}^{2}+{{90}^{2}}={{\left( {{d}_{1}}+80 \right)}^{2}}\Rightarrow {{d}_{1}}=10,625\,cm.$ Chọn D.
| Bài tập 7: Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 24 cm, dao động theo phương thẳng đứng với phương trình là ${{u}_{A}}={{u}_{B}}=a\cos (60\pi t)$(với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là v = 45 cm/s. Gọi MN = 4 cm là đoạn thẳng trên mặt chất lỏng có chung trung trực với AB. Khoảng cách xa nhất giữa MN với AB là bao nhiêu để có ít nhất 5 điểm dao động cực đại nằm trên đoạn MN?
A. 12,7 cm. B. 10,5 cm. C. 14,2 cm. D. 6,4 cm. |
Lời giải chi tiết
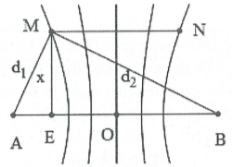
Bước sóng $\lambda =\frac{v}{f}=\frac{45}{30}=1,5$cm
Để trên MN có ít nhất 5 điểm dao động với biên
độ cực đại thì M và N phải thuộc đường cực đại
thứ 2 tính từ cực đại trung tâm.
Xét M ta có ${{d}_{2}}-{{d}_{1}}=k\lambda =2\lambda $ (cực đại thứ 2 nên
k = 2).
Mặt khác $BE=\frac{AB}{2}+\frac{MN}{2}=14,AE=\frac{AB-MN}{2}=10$
Nên $\sqrt{{{x}^{2}}+{{14}^{2}}}-\sqrt{{{x}^{2}}+{{10}^{2}}}=3\xrightarrow{SHIFT-CALC}x=10,5$cm. Chọn B.
| Bài tập 8: Trong thí nghiệm giao thoa trên mặt nước, hai nguồn sóng kết hợp A và B dao động cùng pha, cùng tần số, cách nhau AB = 10 cm tạo ra hai sóng kết hợp có bước sóng $\lambda =4$cm. Trên đường thẳng $\Delta $ song song với AB và cách AB một khoảng là 3 cm, khoảng cách ngắn nhất từ giao điểm C của $\Delta $ với đường trung trực của AB đến điểm M dao động với biên độ cực tiểu là
A. 1,12 cm. B. 0,58 cm. C. 0,56 cm. D. 1,17 cm. |
Lời giải chi tiết
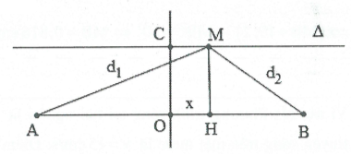
Điểm M dao động với biên độ cực tiểu
khi ${{d}_{1}}-{{d}_{2}}=\left( k+0,5 \right)\lambda $
Điểm M gần C nhất khi k = 0
Khi đó ${{d}_{1}}-{{d}_{2}}=0,5\lambda =2$
Đặt CM = OH = x ta có:
$d_{1}^{2}=M{{H}^{2}}+H{{A}^{2}}={{3}^{2}}+{{\left( 5+x \right)}^{2}}$
$d_{2}^{2}=M{{H}^{2}}+H{{B}^{2}}={{3}^{2}}+{{\left( 5-x \right)}^{2}}$
Suy ra $\sqrt{9+{{\left( 5+x \right)}^{2}}}-\sqrt{9+{{\left( 5-x \right)}^{2}}}=2\xrightarrow{SHIFT-CALC}x=1,17$cm. Chọn D.
| Bài tập 9: Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 25 Hz được đặt tại hai điểm A và B cách nhau 10 cm. Tốc độ truyền sóng trên mặt nước là 40 cm/s. Xét các điểm trên mặt nước thuộc đường thẳng vuông góc với AB tại B, điểm mà phần tử tại đó dao động với biên độ cực đại cách điểm B một đoạn lớn nhất bằng?
A. 32,05 cm B. 30,45 cm C. 41,2 cm D. 10,01 cm |
Lời giải chi tiết
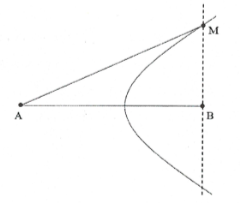
Bước sóng $\lambda =\frac{v}{f}=1,6$cm
M là điểm dao động với biên độ cực đại và cách
điểm B một đoạn lớn nhất $\Rightarrow {{k}_{M}}=1$
$\Rightarrow MA-MB=\lambda =1,6\,cm$
Mặt khác $A{{M}^{2}}-M{{B}^{2}}=A{{B}^{2}}={{10}^{2}}$
$\Rightarrow {{\left( MB+1,6 \right)}^{2}}-M{{B}^{2}}={{10}^{2}}\Leftrightarrow MB=30,45\,cm$
Chọn B
| Bài tập 10: Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 50 Hz được đặt tại hai điểm A và B cách nhau 20 cm. Tốc độ truyền sóng trên mặt nước là 80 cm/s. Xét các điểm trên mặt nước thuộc đường thẳng vuông góc với AB tại B, điểm mà phần tử tại đó dao động với biên độ cực đại cách điểm B một đoạn nhỏ nhất bằng?
A. 0,226 cm B. 0,431 cm C. 0,524 cm D. 0,816 cm |
Lời giải chi tiết
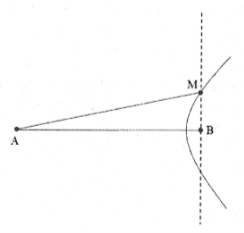
Bước sóng $\lambda =\frac{v}{f}=1,6$cm
Xét $\frac{AB}{\lambda }=12,5$, M là một điểm dao động với
biên độ cực đại và gần B nhất
$\Rightarrow $M nằm trên đường cực đại bậc 12 $\Rightarrow {{k}_{M}}=12$
$\Rightarrow AM-MB=12\lambda =19,2\,cm$
Mặt khác $A{{M}^{2}}-M{{B}^{2}}=A{{B}^{2}}={{20}^{2}}$
$\Rightarrow {{\left( MB+19,2 \right)}^{2}}-M{{B}^{2}}={{20}^{2}}\Leftrightarrow MB=0,816\,cm$. Chọn D
| Bài tập 11: Phương trình sóng tại hai nguồn là $u=a\cos \left( 20\pi t \right)$cm, AB cách nhau 20 cm, vận tốc truyền sóng trên mặt nước là v = 15 cm/s. Điểm M nằm trên đường thẳng vuông góc với AB tại A và dao động với biên độ cực đại. Diện tích tam giác ABM có giá trị cực đại bằng bao nhiêu?
A. 1325,8$c{{m}^{2}}$ B. 2651,6$c{{m}^{2}}$ C. 3024,3$c{{m}^{2}}$ D. 1863,6$c{{m}^{2}}$ |
Lời giải chi tiết
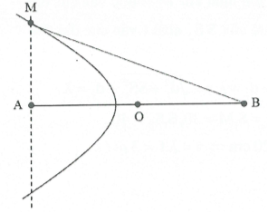
Bước sóng $\lambda =\frac{v}{f}=1,5$cm
Để tam giác ABM có giá trị cực đại thì M phải
nằm trên cực đại bậc 1 $\Rightarrow BM-AM=1,5$cm
Mặt khác ta có: $B{{M}^{2}}-A{{M}^{2}}=A{{B}^{2}}={{20}^{2}}$
$\Rightarrow \left\{ \begin{array}{} BM-AM=1,5 \\ {} B{{M}^{2}}-A{{M}^{2}}={{20}^{2}} \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{} BM=134 \\ {} AM=132,58 \\ \end{array} \right.$
Diện tích tam giác ABM là ${{S}_{\Delta ABM}}=\frac{1}{2}AM.AB=1325,8\,c{{m}^{2}}$. Chọn A.
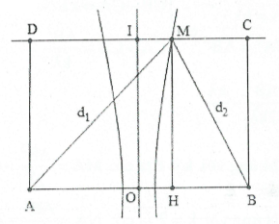
| Bài tập 12: Trên mặt thoáng chất lỏng, tại A và B, người ta bố trí hai nguồn đồng bộ có tần số 16 Hz. Tốc độ truyền sóng trên mặt thoáng chất lỏng v = 80 cm/s. Hình chữ nhật ABCD nằm trên mặt thoáng chất lỏng với AD = 10 cm, I là trung điểm của CD. Gọi điểm M nằm trên CD là điểm gần I nhất dao động với biên độ cực đại. Khoảng cách từ M đến I là 3 cm. Khoảng cách AB là:
A. 20 cm. B. 26,5 cm. C. 30,56 cm. D. 15,28 cm. |
Lời giải chi tiết
Xét điểm M trên CD, M gần I nhất dao động với biên độ cực đại khi M thuộc vân cực đại gần trung trực của AB nhất khi đó: ${{d}_{1}}-{{d}_{2}}=\lambda =\frac{v}{f}=5$cm.
Đặt AB = 2x ta có: $d_{1}^{2}=100+{{\left( x+3 \right)}^{2}}$
$d_{2}^{2}=100+{{\left( x-3 \right)}^{2}}$.
Lại có: $\sqrt{{{x}^{2}}+6x+109}-\sqrt{{{x}^{2}}-6x+109}=5$.
$\xrightarrow{SHIFT-CALC}x=15,28\,cm\Rightarrow AB=2x=30,56\,cm$
Chọn C.
| Bài tập 13: Trên bề mặt chất lỏng có hai nguồn phát sóng kết hợp ${{S}_{1}},{{S}_{2}}$ dao động cùng pha, cách nhau một khoảng ${{S}_{1}}{{S}_{2}}=40$cm. Biết sóng do mỗi nguồn phát ra có tần số f = 15 Hz. Xét điểm M nằm trên đường thẳng vuông góc với ${{S}_{1}}{{S}_{2}}$ tại ${{S}_{1}}$. Đoạn ${{S}_{1}}M$ có giá trị lớn nhất bằng 30 cm để tại M có dao động với biên độ cực đại. Vận tốc truyền sóng trên mặt nước là:
A. v = 2 m/s. B. v = 1,5 m/s. C. v = 1 m/s. D. v = 3 m/s. |
Lời giải chi tiết
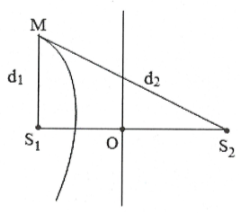
Ta có: $M{{S}_{1}}$ lớn nhất khi M thuộc vân cực đại
gần trung trục của ${{S}_{1}}{{S}_{2}}$ nhất (vân cực đại thứ
nhất).
Khi đó: ${{d}_{2}}-{{d}_{1}}=\lambda \Leftrightarrow \sqrt{d_{1}^{2}+SS_{1}^{2}}-{{d}_{1}}=\lambda $.
Trong đó ${{d}_{1}}={{S}_{1}}M=30,{{S}_{1}}{{S}_{2}}=40.$
Suy ra $\lambda =20\,cm\Rightarrow v=\lambda .f=3\,\,m/s$.
Chọn D
| Bài tập 14: [Trích đề thi THPT QG năm 2016]. Ở mặt chất lỏng có 2 nguồn kết hợp đặt tại A và B dao động điều hòa, cùng pha theo phương thẳng đứng. Ax là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với AB. Trên Ax có những điểm mà các phần tử ở đó dao động với biên độ cực đại, trong đó M là điểm xa A nhất, N là điểm kế tiếp với M, P là điểm kế tiếp với N và Q là điểm gần A nhất. Biết MN = 22,25 cm; NP = 8,75 cm. Độ dài đoạn QA gần nhất với giá trị nào sau đây?
A. 1,2 cm. B. 4,2 cm. C. 2,1 cm. D. 3,1 cm. |
Lời giải chi tiết
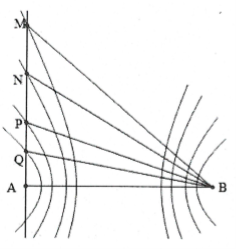
Các điểm M, N, P, Q lần lượt thuộc các dãy cực đại ứng với k = 1; 2; 3; 4.
Xét điểm C bất kì trên Ax dao động với biên độ cực đại ta có:
$\left\{ \begin{array}{} CB-CA=k\lambda \\ {} C{{B}^{2}}-C{{A}^{2}}=A{{B}^{2}} \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} CB-CA=k\lambda \\ {} CA+CB=\frac{A{{B}^{2}}}{k\lambda } \\ \end{array} \right.$
$\Rightarrow CA=\frac{A{{B}^{2}}}{2k\lambda }-\frac{k\lambda }{2}$.
Tại điểm M ứng với k = 1 ta có: $MA=\frac{A{{B}^{2}}}{2\lambda }-0,5\lambda \,\,\left( 1 \right).$
Tại điểm N ứng với k = 2 ta có: $NA=\frac{A{{B}^{2}}}{4\lambda }-\lambda \,\,\left( 2 \right).$
Tại điểm P ứng với k = 3 ta có: $PA=\frac{A{{B}^{2}}}{6\lambda }-1,5\lambda \,\,\left( 3 \right).$
Tại điểm Q ứng với k = 4 ta có: $QA=\frac{A{{B}^{2}}}{8\lambda }-2\lambda \,\,\left( 4 \right).$
Lấy $\left( 1 \right)-\left( 2 \right)\Rightarrow MN=\frac{A{{B}^{2}}}{4\lambda }+0,5\lambda \,=22,25\,cm\,\,\left( 5 \right).$
Lấy $\left( 2 \right)-\left( 3 \right)\Rightarrow NP=\frac{A{{B}^{2}}}{12\lambda }+0,5\lambda \,=8,75\,\left( cm \right)\,\,\left( 6 \right).$
Giải hệ (5) và (6) suy ra $\left\{ \begin{array}{} \frac{A{{B}^{2}}}{\lambda }=81\,cm \\ {} \lambda =4\,cm \\ \end{array} \right.\Rightarrow QA=2,125\,cm.$ Chọn C.
| Bài tập 15: [Trích đề thi đại học năm 2013]. Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp ${{O}_{1}}$ và ${{O}_{2}}$ dao động cùng pha, cùng biên độ. Chọn hệ tọa độ vuông góc xOy (thuộc mặt nước) với gốc tọa độ là vị trí đặt nguồn ${{O}_{1}}$ còn nguồn ${{O}_{2}}$ nằm trên trục Oy. Hai điểm P và Q nằm trên Ox có OP = 4,5 cm và OQ = 8 m. Dịch chuyển nguồn ${{O}_{2}}$ trên trục Oy đến vị trí sao cho góc $\widehat{P{{O}_{2}}Q}$ có giá trị lớn nhất thì phần tử nước tại P không dao động còn phần tử nước tại Q dao động với biên độ cực đại. Biết giữa P và Q không còn cực đại nào khác. Trên đoạn OP, điểm gần P nhất mà các phần tử nước dao động với biên độ cực đại cách P một đoạn là
A. 3,4 cm. B. 2,0 cm. C. 2,5 cm. D. 1,1 cm. |
Lời giải chi tiết
Đặt ${{O}_{1}}{{O}_{2}}=a$ ta có: $\widehat{P{{O}_{2}}Q}={{\varphi }_{2}}-{{\varphi }_{1}}.$
Ta có: $\tan \left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)=\frac{\tan {{\varphi }_{1}}-\tan {{\varphi }_{1}}}{1+\tan {{\varphi }_{1}}\tan {{\varphi }_{2}}}$
$=\frac{\frac{8}{a}-\frac{4,5}{a}}{1+\frac{8}{a}.\frac{4,5}{a}}=\frac{3,5}{a+\frac{36}{a}}\le \frac{3,5}{2\sqrt{a.\frac{36}{a}}}.$
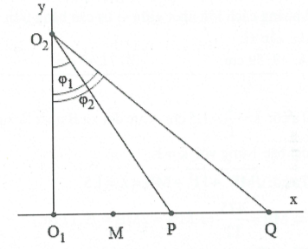
Dấu bằng xảy ra $\Leftrightarrow a=\frac{36}{a}\Leftrightarrow a=6\,cm.$
Khi đó ta có:
$P{{O}_{2}}=\sqrt{{{\left( {{O}_{1}}{{O}_{2}} \right)}^{2}}+{{\left( P{{O}_{1}} \right)}^{2}}}=7,5\,cm$, tương tự $Q{{O}_{2}}=10$cm. Do P dao động với biên độ cực tiểu và Q dao động với biên độ cực đại nên.
$\Rightarrow \left\{ \begin{array}{} P{{O}_{2}}-P{{O}_{1}}=\left( k+0,5 \right)\lambda \\ {} Q{{O}_{2}}-Q{{O}_{1}}=k\lambda \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} \left( k+0,5 \right)\lambda =3 \\ {} k\lambda =2 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} k=1 \\ {} \lambda =2\,cm \\ \end{array} \right.$
Gọi $M\left( 0;x \right)$ là điểm gần P nhất dao động với biên độ cực đại, khi đó M phải nằm trên cực đại thứ 2 ứng với $k=2\Rightarrow M{{O}_{2}}-M{{O}_{1}}=k\lambda \Rightarrow \sqrt{36+{{x}^{2}}}-x=4\Leftrightarrow x=2,5\,\,cm.$
Suy ra $MP={{O}_{1}}P-x=2\,cm.$ Chọn B.
| Bài tập 16: [Trích đề thi thử Chuyên Hạ Long-Quảng Ninh]. Trong thí nghiệm giao thoa sóng mặt nước hai nguồn sóng A và B cách nhau 20 cm, dao động điều hòa theo phương vuông góc với mặt nước có cùng phương trình ${{u}_{A}}={{u}_{B}}=acos20\pi t$(cm) . Tốc độ truyền sóng trên mặt nước là 15 cm/ s biên độ sóng không đổi khi truyền đi. Hai điểm C và D là hai điểm nằm trên mặt nước dao động với biên độ cực đại và tạo với AB thành một hình chữ nhật. Diện tích nhỏ nhất của hình chữ nhật là
A. 2651,6 $c{{m}^{2}}.$ B. 2272$c{{m}^{2}}.$ C. 10,13$c{{m}^{2}}.$ D. 19,53$c{{m}^{2}}.$ |
Lời giải chi tiết
Ta có: $\lambda =\frac{v}{f}=1,5$cm.
Trên AB, dao động cực đại gần A (hoặc B) nhất là: $\left[ \frac{AB}{\lambda } \right]=13$
Để diện tích HCN nhỏ nhất, CD nằm trên cực đại ứng với $k=13$ hoặc $k=-13$.
Tại điểm D ta có: ${{d}_{2}}-{{d}_{1}}=DB-DA=\sqrt{{{20}^{2}}+D{{A}^{2}}}-DA=13\lambda =19,5$cm.
Suy ra: $\left( 400+D{{A}^{2}} \right)={{\left( DA+19,5 \right)}^{2}}\Rightarrow DA=\frac{79}{156}$cm.
Do đó ${{S}_{ABC{{D}_{\min }}}}=\frac{79}{156}.20=10,13\,c{{m}^{2}}.$ Chọn C.
| Bài tập 17: [Trích đề thi thử Chuyên ĐH Vinh 2017]. Trong thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp A và B, cách nhau một khoảng AB = 11 cm dao động cùng pha với tần số là 16 Hz. Tốc độ truyền sóng trên mặt nước là 24 cm/s. Trên đường thẳng vuông góc với AB tại B, khoảng cách lớn nhất giữa vị trí cân bằng trên mặt nước của hai phần tử dao động với biên độ cực đại xấp xỉ: A. 39,59 cm. B. 71,65 cm. C. 79,17 cm. D. 45,32 cm. |
Lời giải chi tiết
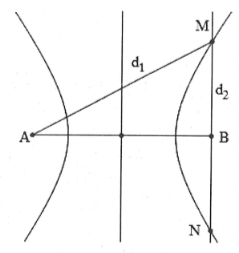
Ta có: $\lambda =\frac{v}{f}=1,5$cm. Cực đại xa B nhất là cực
đại bậc 1 ứng với k = 1.
Ta có: $\sqrt{M{{B}^{2}}+{{11}^{2}}}-MB=\lambda =1,5$
$\Rightarrow MB=\frac{475}{12}\Leftrightarrow MN=2MB=79,17$cm.
Chọn C.
|
Bài tập 18: [Trích đề thi thử THPT Hà Trung – Thanh Hóa]. Hai điểm A và B trên mặt nước cách nhau 12 cm phát ra hai sóng kết hợp có phương trình: ${{u}_{1}}={{u}_{2}}=acos40\pi t$(cm) , tốc độ truyền sóng trên mặt nước là 30 cm/s. Xét đoạn thẳng MN = 6 cm trên mặt nước có chung đường trung trực với AB. Khoảng cách lớn nhất từ MN đến AB sao cho trên đoạn MN chỉ có 5 điểm dao động với biên độ cực đại là A. 10,06 cm. B. 4,5 cm. C. 9,25 cm. D. 6,78 cm. |
Lời giải chi tiết
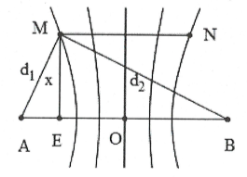
Bước sóng $\lambda =\frac{v}{f}=\frac{30}{20}=1,5$cm
Để trên MN có ít nhất 5 điểm dao động với biên độ cực đại thì
M và N phải thuộc đường cực đại thứ 2 tính từ cực đại trung
tâm.
Xét M ta có ${{d}_{2}}-{{d}_{1}}=k\lambda =2\lambda $ (cực đại thứ 2 nên k = 2).
Mặt khác $BE=\frac{AB}{2}+\frac{MN}{2}=9,AE=\frac{AB-MN}{2}=3$
Nên $\sqrt{{{x}^{2}}+{{9}^{2}}}-\sqrt{{{x}^{2}}+{{3}^{2}}}=3\xrightarrow{SHIFT-CALC}x=10,06\,cm.$ Chọn A.
|
Bài tập 19: [Trích đề thi thử Sở GD{}ĐT Tây Ninh]. Hiện tượng giao thoa sóng mặt nước do hai nguồn điểm A, B kết hợp và đồng pha, cách nhau 48 cm gây ra. Tại điểm M trên mặt nuớc, với MA vuông góc với AB và MA= 36 cm thì M trên một đường cực tiểu giao thoa, còn MB cắt đường tròn đường kính AB tại N thì N trên một đường cực đại giao thoa, giữa M và N chỉ có một đường cực đại giao thoa, không kể đường qua N, bước sóng là: A. 4,8 cm. B. 3,2 cm. C. 9,6 cm. D. 6,4 cm. |
Lời giải chi tiết
Tam giác ABM vuông tại A có đường cao AN.
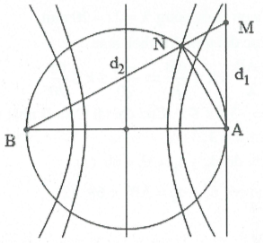
Ta có: $MB=\sqrt{M{{A}^{2}}+A{{B}^{2}}}=60$cm.
Khi đó $NB=\frac{A{{B}^{2}}}{MB}=38,4\,cm,\,AN=28,8\,cm.$
Ta có: $NB-NA=k\lambda =9,6$.
Khi đó M thuộc dãy $\left( k+1+0,5 \right)\lambda .$
$=9,6+1,5\lambda =MB-MA=24\Rightarrow \lambda =9,6\,cm.$
Chọn C.
|
Bài tập 20: [Trích đề thi thử Sở GD{}ĐT Vĩnh Phúc]. Tại mặt chất lỏng có hai nguồn phát sóng kết hợp A, B cách nhau 16 cm, dao động điều hòa theo phương vuông góc mặt chất lỏng với phương trình: ${{u}_{A}}=2\cos 40\pi t$(cm) và ${{u}_{B}}=2\cos \left( 40\pi t+\pi \right)$(cm). Tốc độ truyền sóng trên mặt chất lỏng là 40 cm/s. M là một điểm trên đường thẳng Ax vuông góc với AB mà tại đó các phần tử chất lỏng dao động với biên độ cực đại. Khoảng cách AM ngắn nhất bằng: A. 4,28 cm. B. 2,07 cm. C. 1,03 cm. D. 2,14 cm. |
Lời giải chi tiết
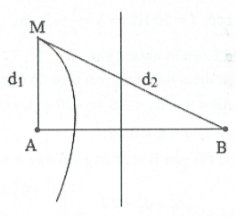
Ta có $\lambda =\frac{v}{f}=2$. Số vân dao động với biên độ dao động cực
đại trên đoạn AB thỏa mãn điều kiện:
$-AB\le \left( k+0,5 \right)\lambda \le AB.$
Hay: $\frac{-AB}{\lambda }-0,5\le k\le \frac{AB}{\lambda }-0,5\Leftrightarrow -8,5\le k\le 7,5$
$\Leftrightarrow -8\le k\le 7\left( k\in \mathbb{N} \right)$.
Đoạn AM có giá trị bé nhất thì M phải nằm trên đường cực
đại bậc 7 $\left( 7,5\lambda \right)$(cực đại xa trung trực AB nhất). Khi đó
${{d}_{2}}-{{d}_{1}}=7,5\lambda =15\,cm.$
Mặt khác, do tam giác AMB là tam giác vuông tại A nên ta có:
${{d}_{2}}=BM=\sqrt{A{{M}^{2}}+A{{B}^{2}}}=\sqrt{d_{1}^{2}+{{8}^{2}}}$
Suy ra $\sqrt{d_{1}^{2}+{{16}^{2}}}-{{d}_{1}}=15\,cm\Leftrightarrow d_{1}^{2}+{{16}^{2}}={{\left( {{d}_{1}}+15 \right)}^{2}}\Rightarrow {{d}_{1}}=1,03\,cm.$ Chọn C.
|
Bài tập 21: [Trích đề thi THPT QG năm 2016]. Tại mặt nước, hai nguồn kết hợp được đặt ở A và B cách nhau 68 mm, dao động điều hòa cùng tần số, cùng pha, theo phương vuông góc với mặt nước. Trên đoạn AB, hai phần tử nước dao động với biên độ cực đại có vị trí cân bằng cách nhau một đoạn ngắn nhất là 10 mm. Điểm C là vị trí cân bằng của phần tử ở mặt nước sao cho $AC\bot BC$. Phần tử nước ở C dao động với biên độ cực đại. Khoảng cách BC lớn nhất bằng A. 37,6 mm. B. 67,6 mm. C. 64,0 mm. D. 68,5 mm. |
Lời giải chi tiết
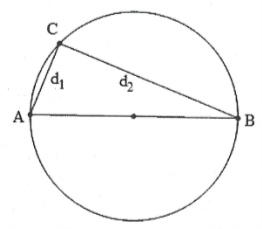
Ta có bước sóng $\lambda =2.i=20\,mm$
Cực đại trên AB thỏa mãn
$\frac{-AB}{\lambda }\le k\le \frac{AB}{\lambda }\Leftrightarrow \frac{-68}{20}\le k\le \frac{68}{20}$
$\Leftrightarrow -3\le k\le 3$. Cực đại tại C xa B nhất ứng
với k = 3.
Khi đó ${{d}_{2}}-{{d}_{1}}=3\lambda =60\,\,\left( 1 \right).$
Lại có: $d_{1}^{2}+d_{2}^{2}=A{{B}^{2}}={{68}^{2}}\,\,\left( 2 \right).$
Từ (1) và (2) suy ra: ${{\left( {{d}_{2}}-60 \right)}^{2}}+d_{2}^{2}={{68}^{2}}\Rightarrow {{d}_{2}}=67,58\,mm.$ Chọn B.
|
Bài tập 22: Trên mặt nước có hai nguồn kết hợp A, B dao động với các phương trình ${{u}_{A}}=acos\left( 100\pi t \right)$;${{u}_{B}}=acos\left( 100\pi t+\pi \right)$. Biết AB = 20 cm và vận tốc truyền sóng là l,5 m/s. Điểm M dao động với biên độ cực đại trên đuờng tròn đường kính AB và gần B nhất cách AB một khoảng bằng: A. 9,75 mm. B. 10,97 mm. C. 6,32 mm. D. 4,94 mm. |
Lời giải chi tiết
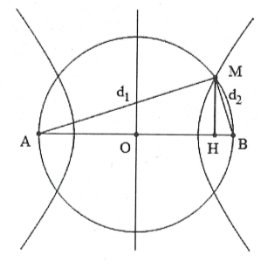
Ta có: $f=50Hz\Rightarrow \lambda =\frac{v}{f}=3\,cm.$
Do 2 nguồn ngược pha.
Xét điểm dao động với biên độ cực đại trên AB.
$-AB<{{d}_{1}}-{{d}_{2}}<AB\Leftrightarrow -20<\left( k+0,5 \right)\lambda <20$
$\Leftrightarrow -7,17<k<6,16$
Cực đại gần B nhất ứng với dãy k = 6 (dãy $6,5\lambda $).
Khi đó $\left\{ \begin{array}{} d_{1}^{2}+d_{2}^{2}={{20}^{2}} \\ {} {{d}_{1}}-{{d}_{2}}=19,5 \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{} d_{1}^{2}+d_{2}^{2}={{20}^{2}} \\ {} {{d}_{1}}{{d}_{2}}=\frac{d_{1}^{2}+d_{2}^{2}-{{\left( {{d}_{1}}-{{d}_{2}} \right)}^{2}}}{2}=9,875 \\ \end{array} \right.$
Do đó: $MH=\frac{MA.MB}{AB}=\frac{{{d}_{1}}{{d}_{2}}}{20}=0,49375\,cm=4,94\,mm.$ Chọn D.
|
Bài tập 23: Trên mặt nước có hai nguồn kết hợp A, B dao động ngược pha và cách nhau 50 cm, bước sóng do sóng từ các nguồn phát ra là $\lambda =6$cm. Điểm M dao động với biên độ cực đại trên đường tròn đường kính AB cách xa đường trung trực nhất một khoảng bằng A. 24,54 cm. B. 4,74 cm. C. 23,24 cm. D. 49,77 cm. |
Lời giải chi tiết
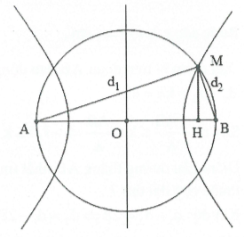
Xét điểm dao động với biên độ cực đại trên AB.
Ta có: $-AB<{{d}_{1}}-{{d}_{2}}<AB.$ (hai nguồn ngược pha)
$\Leftrightarrow -50<\left( k+0,5 \right)\lambda <50\Leftrightarrow -8,83<k<7,83.$
Cực đại gần B nhất (xa trung trực AB nhất) ứng với dãy
$k=7\left( 7,5\lambda \right)$. Khi đó ta có
$\left\{ \begin{array}{} d_{1}^{2}+d_{2}^{2}={{50}^{2}} \\ {} {{d}_{1}}-{{d}_{2}}=45 \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{} d_{1}^{2}+d_{2}^{2}={{50}^{2}} \\ {} {{d}_{1}}{{d}_{2}}=\frac{d_{1}^{2}+d_{2}^{2}-{{\left( {{d}_{2}}-{{d}_{1}} \right)}^{2}}}{2}=\frac{475}{2} \\ \end{array} \right.$
Mặt khác $OH=\sqrt{O{{M}^{2}}-M{{H}^{2}}}=\sqrt{{{25}^{2}}-\frac{M{{A}^{2}}.M{{B}^{2}}}{M{{A}^{2}}+M{{B}^{2}}}}=24,54\,cm.$ Chọn A.
|
Bài tập 24: Trên mặt nước có hai nguồn kết hợp A, B dao động với các phương trình ${{u}_{A}}={{u}_{B}}=acos(\omega t+\varphi )$, bước sóng hai nguồn phát ra là $\lambda (\lambda <\text{ }AB)$. Điểm M dao động với biên độ cực đại trên đường tròn đường kính AB và gần trung trực của AB nhất cách AB một khoảng bằng: A. $\frac{A{{B}^{2}}-{{\lambda }^{2}}}{AB}.$ B. $\frac{A{{B}^{2}}-{{\lambda }^{2}}}{2AB}.$ C. $\frac{A{{B}^{2}}+{{\lambda }^{2}}}{AB}.$ D. $\frac{A{{B}^{2}}+{{\lambda }^{2}}}{2AB}.$ |
Lời giải chi tiết
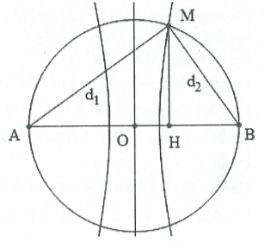
Điều kiện cực đại là ${{d}_{1}}-{{d}_{2}}=k\lambda .$
Cực đại gần trung trực của AB nhất là dãy cực đại số 1 ứng
với k = 1.
Khi đó ${{d}_{1}}-{{d}_{2}}=\lambda $ suy ra $\left\{ \begin{array}{} {{d}_{1}}-{{d}_{2}}=\lambda \\ {} d_{1}^{2}+d_{2}^{2}=A{{B}^{2}} \\ \end{array} \right.$
Suy ra ${{d}_{1}}{{d}_{2}}=\frac{d_{1}^{2}+d_{2}^{2}-{{\left( {{d}_{1}}-{{d}_{2}} \right)}^{2}}}{2}=\frac{A{{B}^{2}}-{{\lambda }^{2}}}{2}.$
Do đó: $MH=\frac{{{d}_{1}}{{d}_{2}}}{AB}=\frac{A{{B}^{2}}-{{\lambda }^{2}}}{2AB}.$ Chọn B.
|
Bài tập 25: Giao thoa sóng nước với hai nguồn giống hệt nhau A, B cách nhau 30 cm có tần số 25 Hz. Tốc độ truyền sóng trên mặt nước là 1 m/s . Trên mặt nước xét đường tròn tâm A, bán kính AB. Điểm trên đường tròn dao động với biên độ cực đại cách đường thẳng qua A, B một đoạn gần nhất là: A. 18,96 mm. B. 17,86 mm. C. 14,93 mm. D. 19,99 mm. |
Lời giải chi tiết
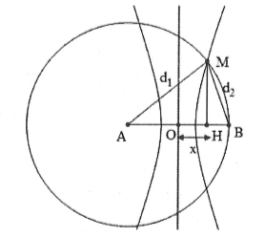
Bước sóng $\lambda =\frac{v}{f}=4$cm.
Xét điểm N trên đoạn AB dao động với biên độ cực đại:
${{d}_{1}}-{{d}_{2}}=k\lambda =4k$
Suy ra $\frac{-AB}{\lambda }\le k\le \frac{AB}{\lambda }\Rightarrow -7,5\le k\le 7,5$
Điểm gần đường thẳng AB nhất ứng với dãy k = 7. Điểm M
thuộc cực đại thứ 7.
Khi đó: ${{d}_{1}}-{{d}_{2}}=28\Rightarrow {{d}_{2}}={{d}_{1}}-28=2\,cm$
Xét tam giác AMB dựng MH = h vuông góc với AB. Đặt OH = x.
Khi đó: ${{h}^{2}}=d_{1}^{2}-{{\left( OA+x \right)}^{2}}=d_{2}^{2}-{{\left( OB-x \right)}^{2}}$
$\Leftrightarrow {{30}^{2}}-{{\left( 15+x \right)}^{2}}={{2}^{2}}-{{\left( 15-x \right)}^{2}}\Rightarrow x=\frac{224}{15}\Rightarrow h=19,99\,mm.$ Chọn D.
|
Bài tập 26: Trên mặt nước có hai nguồn kết hợp A, B dao động ngược pha và cách nhau 24 cm, bước sóng do sóng từ các nguồn phát ra là $\lambda =3$cm. Điểm M dao động với biên độ cực tiểu trên đường tròn tâm A bán kính AB và gần trung trực của AB nhất cách trung trực một đoạn bằng: A. 2,81 cm. B. 1,92 cm. C. 3,37 cm. D. 1,91 cm. |
Lời giải chi tiết
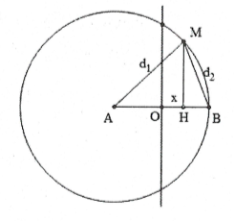
Hai nguồn ngược pha và cực tiểu gần trung trực của AB nhất ứng
với dãy k = 1. (về phía điểm B).
Do đó ta có: $MA-MB=\lambda =3$
Lại có: $AM=AB=24\Rightarrow MB=MA-3=21\,cm$
Đặt OH = x ta có: $M{{H}^{2}}=M{{A}^{2}}-A{{H}^{2}}=M{{B}^{2}}-H{{B}^{2}}$.
$\Leftrightarrow {{24}^{2}}-{{\left( 12+x \right)}^{2}}={{21}^{2}}-{{\left( 12-x \right)}^{2}}\Rightarrow x=2,8125\,cm.$
Chọn A.
Chú ý: Ta có thể đặt $AH=x\Rightarrow HB=24-x.$
Khi đó: ${{24}^{2}}-{{x}^{2}}={{21}^{2}}-{{\left( 24-x \right)}^{2}}\Rightarrow x=14,8125\Rightarrow OH=x-12=2,81.$
|
Bài tập 27: Trong hiện tượng giao thoa sóng hai nguồn kết hợp A, B cách nhau 20 cm dao động điều hòa cùng pha cùng tần số f = 25 Hz. Tốc độ truyền sóng trên mặt nước là 0,5 m/s. Xét trên đường tròn tâm A bán kính AB, điểm M nằm trên đường tròn dao động với biên độ cực đại cách đường thẳng AB một đoạn xa nhất bằng: A. 20,003 cm. B. 19,968 cm. C. 19,761 cm. D. 19,996 cm. |
Lời giải chi tiết
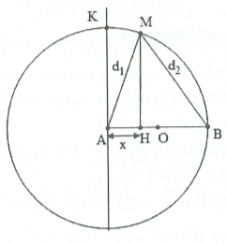
Ta có: $\lambda =\frac{v}{f}=2$cm. Hai nguồn cùng pha nên cực đại giao thoa
thoả mãn $MB-MA=k\lambda =2k.$
Cực đại xa AB nhất là cực đại gần điểm K nhất.
Giải $\frac{KB-KA}{2}=\frac{20\sqrt{2}-20}{2}=4,14\Rightarrow $Chọn k = 4
Suy ra $MB-MA=8\Rightarrow MB=MA+8=28$
Đặt $AH=x\Rightarrow M{{H}^{2}}=A{{M}^{2}}-{{x}^{2}}=M{{B}^{2}}-{{\left( 20-x \right)}^{2}}$
$\Rightarrow {{20}^{2}}-{{x}^{2}}={{28}^{2}}-{{\left( 20-x \right)}^{2}}\Rightarrow x=0,4\,cm.$
Suy ra $MH=\sqrt{A{{M}^{2}}-{{x}^{2}}}=19,996\,\,cm.$ Chọn D.
|
Bài tập 28: Trên mặt nước có hai nguồn kết hợp A, B dao động cùng pha và cách nhau 18 cm, bước sóng do sóng từ các nguồn phát ra là 4 cm. Điểm M dao động với biên độ cực đại trên đường tròn tâm A bán kính AB và cách đường thẳng AB lớn nhất. Khoảng cách từ M tới trung trực của AB bằng A. 13,55 cm. B. 7 cm. C. 9,78 cm. D. 4,45 cm. |
Lời giải chi tiết
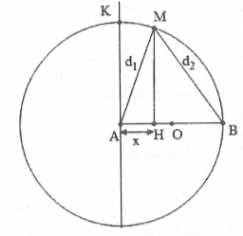
Hai nguồn cùng pha nên cực đại giao thoa thoả mãn
$MB-MA=k\lambda =4k.$
Cực đại xa AB nhất là cực đại gần điểm K nhất.
Giải $\frac{KB-KA}{4}=\frac{18\sqrt{2}-18}{4}=1,86\Rightarrow $Chọn k = 2.
Suy ra $MB-MA=8\Rightarrow MB=MA+8=26.$
Đặt $AH=x\Rightarrow M{{A}^{2}}-{{x}^{2}}=M{{B}^{2}}-{{\left( 18-x \right)}^{2}}=M{{H}^{2}}.$
$\Rightarrow x=-0,78\,cm\Rightarrow OH=9,78\,cm.$
Chú ý: x < 0 chứng tỏ H nằm ngoài khoảng AB, tức
là điểm M nằm bên trái điểm K. Chọn C.
|
Bài tập 29: Trong hiện tượng giao thoa sóng hai nguồn kết hợp A, B cách nhau 20 cm dao động điều hòa cùng pha cùng tần số f = 50 Hz . Tốc độ truyền sóng trên mặt nước là 1,5 m/s. Xét trên đường tròn tâm A bán kính AB, điểm M nằm trên đường tròn dao động với biên độ cực đại, gần đường trung trực của AB nhất một khoảng bằng bao nhiêu: A. 27,75 mm. B. 26,1 mm. C. 19,76 mm. D. 32,4 mm. |
Lời giải chi tiết
Bước sóng $\lambda =\frac{v}{f}=3$cm.
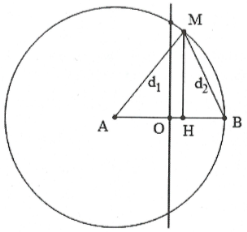
Điểm M dao động với biên độ cực đại gần trung trực của
AB nhất là dãy cực đại số một nằm về phía bên phải
trung trực.
Khi đó ${{d}_{1}}-{{d}_{2}}=\lambda =3\Rightarrow {{d}_{2}}={{d}_{1}}-3=17$cm.
Đặt AH = x ta có:
$M{{H}^{2}}=d_{1}^{2}-A{{H}^{2}}=d_{2}^{2}-B{{H}^{2}}$
$\Leftrightarrow {{20}^{2}}-{{x}^{2}}={{17}^{2}}-{{\left( 20-x \right)}^{2}}\Rightarrow x=12,775\,cm$
Do đó $OH=x-OA=2,775\text{ }cm=27,75\text{ }mm$.
Chọn A.
|
Bài tập 30: [Trích đề thi đại học năm 2012]. Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 50 Hz được đặt tại hai điểm ${{S}_{1}}$ và ${{S}_{2}}$ cách nhau 10 cm. Tốc độ truyền sóng trên mặt nước là 75 cm/s. Xét các điểm trên mặt nước thuộc đường tròn tâm ${{S}_{1}}$, bán kính ${{S}_{1}}{{S}_{2}}$, điểm mà phần tử tại đó dao động với biên độ cực đại cách điểm ${{S}_{2}}$ một đoạn ngắn nhất bằng A. 85 mm. B. 15 mm. C. 10 mm. D. 89 mm. |
Lời giải chi tiết
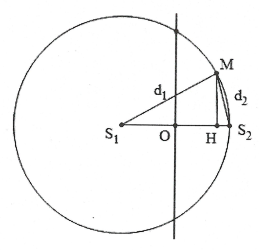
Bước sóng $\lambda =\frac{v}{f}=1,5$cm
Hai nguồn cùng pha nên điều kiện cực đại là:
${{d}_{1}}-{{d}_{2}}=k\lambda $
Xét các điểm cực đại trên ${{S}_{1}}{{S}_{2}}$.
$-\frac{{{S}_{1}}{{S}_{2}}}{\lambda }<k<\frac{{{S}_{1}}{{S}_{2}}}{\lambda }\Leftrightarrow -6,67<k<6,67.$
Cực đại gần ${{S}_{2}}$ nhất là dãy ứng với k = 6.
Khi đó: $\left\{ \begin{array}{} {{d}_{1}}-{{d}_{2}}=6.1,5=9\,cm \\ {} {{d}_{1}}={{S}_{1}}{{S}_{2}}=10\,cm \\ \end{array} \right.\Rightarrow {{d}_{2}}=1\,cm$
Vậy ${{d}_{2}}=10$mm. Chọn C.
|
Bài tập 31: [Trích đề thi Chuyên Lê Hồng Phong – Nam Định]. Trên mặt thoáng của một chất lỏng có hai nguồn sóng A, B cách nhau 10 cm, dao động cùng pha, cùng tần số f = 15 Hz. Gọi $\Delta $ là đường trung trực của AB. Xét trên đường tròn đường kính AB, điểm mà phần tử ở đó dao động với biên độ cực đại cách $\Delta $ một khoảng nhỏ nhất là 1,4 cm. Tốc độ truyền sóng trên mặt chất lỏng là: A. 0,42 m/s. B. 0,84 m/s. C. 0,30 m/s. D. 0,60 m/s. |
Lời giải chi tiết
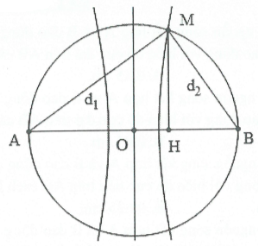
Điều kiện cực đại là ![]() .
.
Cực đại gần trung trực của AB nhất là dãy cực
đại số 1 ứng với k = 1.
Khi đó ${{d}_{1}}-{{d}_{2}}=\lambda $. Ta có: $OH={{d}_{min}}=1,4$cm.
Suy ra $MH=\sqrt{O{{M}^{2}}-O{{H}^{2}}}=4,8$cm.
Ta có: $\left\{ \begin{array}{} {{d}_{1}}=\sqrt{M{{H}^{2}}+A{{H}^{2}}} \\ {} {{d}_{2}}=\sqrt{M{{H}^{2}}+H{{B}^{2}}} \\ \end{array} \right.\Rightarrow {{d}_{1}}-{{d}_{2}}=2=\lambda $
$\Rightarrow v=\lambda f=0,3\,m/s$. Chọn C.
|
Bài tập 32: Trên mặt nước có hai nguồn kết hợp A, B cách nhau 15 cm, dao động với các phương trình ${{u}_{A}}=a\cos \left( \omega t+\frac{\pi }{2} \right)$cm; ${{u}_{B}}=a\cos \left( \omega t-\frac{\pi }{6} \right)$cm; $\lambda =2$cm. M là điểm trên đường thẳng By vuông góc với AB tại B và cách A một khoảng 20 cm. Điểm dao động với biên độ cực đại trên AM cách A một khoảng xa nhất bằng A. 18,9 cm. B. 18,7 cm. C. 19,7 cm. D. 19,6 cm. |
Lời giải chi tiết
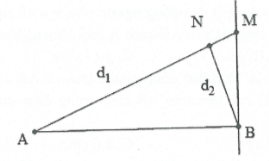
Điểm cực đại trên AM thỏa mãn $MB-MA<{{d}_{2}}-{{d}_{1}}<AB$.
$\Leftrightarrow \sqrt{M{{A}^{2}}-A{{B}^{2}}}-MA<k\lambda +\frac{{{\varphi }_{2}}-{{\varphi }_{1}}}{2\pi }\lambda <AB\Leftrightarrow -6,77<\left( k-\frac{1}{3} \right)\lambda <15$
$\Leftrightarrow -3,05<k<7,83\Rightarrow $ cực đại xa A nhất ứng với $k=-3$(đầu phía điểm M).
Khi đó: $NB-NA=\frac{-20}{3};\,N{{A}^{2}}+A{{B}^{2}}-2NA.AB\cos A=N{{B}^{2}}$
$\begin{array}{} \Leftrightarrow \left\{ \begin{array}{} {{d}_{2}}-{{d}_{1}}=\frac{-20}{3} \\ {} d_{1}^{2}+{{15}^{2}}-2.{{d}_{1}}.15.\frac{15}{20}=d_{2}^{2} \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} {{d}_{2}}-{{d}_{1}}=\frac{-20}{3} \\ {} {{15}^{2}}-2.{{d}_{1}}.15.\frac{15}{20}=\left( {{d}_{2}}-{{d}_{1}} \right)\left( {{d}_{2}}+{{d}_{1}} \right) \\ \end{array} \right. \\ {} \\ \end{array}$
$\Leftrightarrow \left\{ \begin{array}{} {{d}_{2}}-{{d}_{1}}=\frac{-20}{3} \\ {} \frac{-20}{3}\left( {{d}_{2}}+{{d}_{1}} \right)+\frac{45}{2}{{d}_{1}}={{15}^{2}} \\ \end{array} \right.\Rightarrow {{d}_{1}}=19,7\,cm.$ Chọn C.
