DẠNG 5: CHUYỂN ĐỘNG CỦA ELECTRON TRONG ĐIỆN TRƯỜNG VÀ TỪ TRƯỜNG.
Hiện tượng quang điện trong điện trường.
– Một hạt mang điện bay vào điện trường $\overrightarrow{E}$ sẽ chịu tác dụng của lực điện trường làm cho hạt chuyển động với gia tốc $a:\overrightarrow{{{F}_{d}}}=q.\overrightarrow{E}=m\overrightarrow{a}$
Với $q>0:\overrightarrow{{{F}_{d}}}$ cùng chiều với $\overrightarrow{E};q<0:\overrightarrow{{{F}_{d}}}$ ngược chiều với $\overrightarrow{E}$.
Công của lực điện trường sinh ra để làm thay đổi động năng của hạt:
$A=q{{U}_{12}}=\frac{1}{2}mv_{2}^{2}-\frac{1}{2}mv_{1}^{2}$
Điện thế hãm của tấm kim loại cô lập:
+) Chiếu chùm photon có bước sóng thích hợp vào một quả cầu kim loại (tích điện âm hoặc không tích điện) làm các electron quang điện bứt dần ra khỏi quả cầu. Đến một lúc nào đó quả cầu tích điện dương.
+) Electron quang điện nằm trong vùng điện trường của quả cầu bị chịu tác dụng của lực điện và làm nó chuyển động chậm dần với gia tốc a; electron quang điện có vận tốc cực đại lớn nhất sẽ đi xa nhất và thoát ra vùng kiểm soát của điện trường. Các electron bứt ra ngày càng nhiều, quả cầu tích điện dương không đủ lớn thì electron có động năng lớn nhất cũng bị hút ngược trở lại. Khi đó, quả cầu không thể mất thêm điện tích nữa, điện thế của quả cầu đạt trạng thái bão hoà ${{V}_{h}}$.
+) Điện thế hãm ${{V}_{h}}$ là điện thế cao nhất của tấm kim loại, khiến cho các electron có động năng lớn nhất cũng không thoát ra được. Ta có $e{{V}_{h}}=\frac{mv_{\text{max}}^{2}}{2}=\varepsilon -A.$.
VÍ DỤ MINH HỌA
| Bài tập 17: Cho một tấm kim loại cô lập, trung hoà về điện, có công thoát bằng 4,47 eV. Kích thích liên tục bằng ánh sáng có bước sóng bằng 0,14 $\mu m$ (trong chân không). Lấy mốc tính điện thế ở xa vô cùng. Điện thế cao nhất mà tấm kim loại có thể đạt được là
A. 4,403 V. B. 3,533 V. C. 3,72 V. D. 1,57 V. |
Lời giải chi tiết
Ta có: $e{{V}_{h}}=\frac{mv_{\text{max}}^{2}}{2}=\varepsilon -A.$
$\Rightarrow {{V}_{h}}=\frac{\varepsilon -A.}{e}=\frac{\frac{hc}{\lambda }-A}{e}=\frac{\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{0,{{14.10}^{-6}}}-4,{{47.10}^{-19}}.1,{{6.10}^{-19}}}{1,{{6.10}^{-19}}}\approx 4,4$ V. Chọn A.
| Bài tập 18: [Trích đề thi THPT QG năm 2008]. Khi chiếu lần lượt hai bức xạ có tần số là ${{f}_{1}},{{f}_{2}}$ (với ${{f}_{1}}<{{f}_{2}}$) vào một quả cầu kim loại đặt cô lập thì đều xảy ra hiện tượng quang điện với điện thế cực đại của quả cầu lần lượt là ${{V}_{1}},{{V}_{2}}$. Nếu chiếu đồng thời hai bức xạ trên vào quả cầu này thì điện thế cực đại của nó là
A. ${{V}_{2}}$. B. $\left( {{V}_{1}}+{{V}_{2}} \right)$. C. ${{V}_{1}}$. D. $\left| {{V}_{1}}-{{V}_{2}} \right|$. |
Lời giải chi tiết
Với bức xạ ${{f}_{1}}:e{{V}_{h1}}=\frac{mv_{\text{max1}}^{2}}{2}=h{{f}_{1}}-A.$
Với bức xạ ${{f}_{2}}:e{{V}_{h2}}=\frac{mv_{\text{max2}}^{2}}{2}=h{{f}_{2}}-A.$
Chiếu đồng thời hai bức xạ ${{f}_{1}},{{f}_{2}}$: do ${{f}_{2}}>{{f}_{1}}\Rightarrow {{V}_{h2}}>{{V}_{h1}}$ nên điện thế cực đại của nó là ${{V}_{h2}}$.
Vậy nếu chiếu đồng thời nhiều bức xạ ${{f}_{1}},{{f}_{2}},…,{{f}_{n}}$ vào một tấm kim loại thì ${{f}_{\text{max}}}$ quyết định ${{V}_{h}}$ của tấm kim loại đó. Chọn A.
| Bài tập 19: Chiếu liên tục các bức xạ có bước sóng $\lambda $ hoặc $3\lambda $ lên bề mặt một tấm kim loại cô lập không tích điện thì hiệu điện thế cực đại của tấm kim loại so với đất tương ứng là 7 V hoặc 1 V. Nếu chiếu liên tục bức xạ có bước sóng $4\lambda $ lên tấm kim loại cô lập không tích điện này thì hiệu điện thế cực đại của tấm kim loại so với đất là
A. 0,75 V. B. 4 V. C. 0,5 V. D. 0,25 V. |
Lời giải chi tiết
Với bức xạ $\lambda :e{{V}_{h1}}=\frac{hc}{\lambda }-A\Leftrightarrow 7\text{e}=\frac{hc}{\lambda }-A\Leftrightarrow 7=\frac{hc}{e\lambda }-\frac{A}{e}\left( 1 \right)$
Với bức xạ $3\lambda :e{{V}_{h3}}=\frac{hc}{\lambda }-A\Leftrightarrow 1\text{e}=\frac{hc}{3\lambda }-A\Leftrightarrow 1=\frac{hc}{e\lambda }-\frac{A}{e}\left( 2 \right)$
Giải (1) và (2), được: $\frac{hc}{e\lambda }=9;\frac{A}{e}=2.$
Với bức xạ $4\lambda :e{{V}_{h4}}=\frac{hc}{4\lambda }-A\Leftrightarrow {{V}_{h4}}=\frac{hc}{4\text{e}\lambda }-\frac{A}{e}=\frac{9}{4}-2=0,25$ V. Chọn D.
| Bài tập 20: Cho một tấm kim loại cô lập, trung hoà về điện, có công thoát êlectron bằng 3 eV. Chiếu sáng liên tục tấm kim loại bằng ánh sáng đơn sắc có bước sóng nhỏ hơn giới hạn quang điện của kim loại, lấy mốc tính điện thế ở xa vô cùng, thì thấy điện thế cực đại của tấm kim loại đạt được là 6 V. Bước sóng kích thích xấp xỉ bằng
A. 0,138 $\mu m$. B. 1,38 $\mu m$. C. 0,318 $\mu m$. D. 3,18 $\mu m$. |
Lời giải chi tiết
Ta có: $e{{V}_{h}}=\frac{hc}{\lambda }-A\Rightarrow \frac{hc}{\lambda }=e{{V}_{h}}+A$
$\Rightarrow \lambda =\frac{hc}{e{{V}_{h}}+A}=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{1,{{6.10}^{-19}}.3+3.1,{{6.10}^{-19}}}=1,{{38.10}^{-7}}m=0,138\mu m$. Chọn A.
| Bài tập 21: Chiếu liên tục các bức xạ có tần số f hoặc 3f lên bề mặt một tấm kim loại cô lập không tích điện thì hiệu điện thế cực đại của tấm kim loại so với đất tương ứng là 2 V hoặc 8 V. Tần số nhỏ nhất của bức xạ có thể gây ra hiện tượng quang điện đối với bản kim loại nói trên là
A. f/5. B. f/4. C. f/3. D. f/2. |
Lời giải chi tiết
Với bức xạ $f:e{{V}_{h1}}=hf-A\Leftrightarrow 2=\frac{hf}{e}-\frac{A}{e}\left( 1 \right)$
Với bức xạ $3f:e{{V}_{h3}}=hf-A\Leftrightarrow 8=3\frac{hf}{e}-\frac{A}{e}\left( 2 \right)$
Giải (1), (2) được: $\frac{hf}{e}=3;\frac{A}{e}=1\Rightarrow \frac{A}{h}=\frac{f}{3}$.
Tần số nhỏ nhất khi năng lượng photon vừa đúng bằng công thoát của kim loại:
$h{{f}_{\min }}-A=0\Rightarrow {{f}_{\min }}=\frac{A}{h}=\frac{f}{3}$. Chọn C.
– Chuyển động của electron quang điện trong điện trường đều:
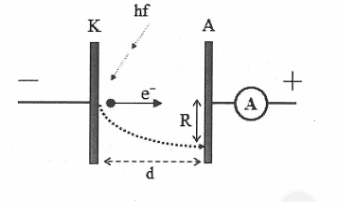
+) Chiếu vào một điểm cố định trên catôt tia sáng có bước sóng $\lambda $ vào một tế bào quang điện có anôt và catôt đều là những bản kim loại phẳng, đặt song song, đối diện và cách nhau một khoảng d. Đặt vào anôt và catôt một hiệu điện thế ${{U}_{AK}}\left( {{U}_{AK}}>0 \right)$.
+) Sau khi bứt ra khỏi catôt, electron bay theo mọi phương, dưới tác dụng của lực điên electron sẽ đến anôt với bán kính lớn nhất ${{R}_{\text{max}}}$ khi bay ra khỏi catôt nó có phương song song với bề mặt catôt. Với các electron này sẽ tham gia đồng thời hai chuyển động:
Chuyển động theo phương song song với bề mặt catôt (phương Ox) với vận tốc ban đầu ${{v}_{om\text{ax}}}$.
Phương trình chuyển động có dạng: $x={{v}_{om\text{ax}}}t\left( 1 \right)$
Chuyển động ngược chiều cường độ điện trường (theo phương Oy) với gia tốc $\overrightarrow{a}$ có độ lớn:
$a=\frac{\left| {{F}_{d}} \right|}{m}=\frac{\left| q \right|E}{m}=\frac{\left| q \right|{{U}_{AK}}}{m\text{d}}\left( 2 \right)$
Phương trình chuyển động theo phương Oy có dạng:
$y={{v}_{oy}}t+\frac{1}{2}a{{t}^{2}}=\frac{1}{2}a{{t}^{2}}$
Khi $x={{R}_{\text{max}}}$ thì y = d, ta có: $d=\frac{1}{2}a{{t}^{2}}\Rightarrow t=\sqrt{\frac{2\text{d}}{a}}$.
Thay vào (1), ta được: $x={{R}_{\text{max}}}={{v}_{om\text{ax}}}t={{v}_{om\text{ax}}}\sqrt{\frac{2\text{d}}{a}}\left( 3 \right)$
Trong đó: ${{v}_{om\text{ax}}}$ được xác định thông qua công thức Anh-xtanh:
$\varepsilon -A=\frac{1}{2}mv_{om\text{ax}}^{2}\Rightarrow {{v}_{om\text{ax}}}=\sqrt{\frac{2\left( \varepsilon -A \right)}{m}}\left( 4 \right)$
Thay (2) và (4) vào (3), ta được:
${{R}_{\text{max}}}={{v}_{om\text{ax}}}\sqrt{\frac{2\text{d}}{a}}=\sqrt{\frac{2\left( \varepsilon -A \right)}{m}}.\sqrt{\frac{2\text{d}}{\frac{\left| q \right|{{U}_{AK}}}{m\text{d}}}}=2\text{d}\sqrt{\frac{\varepsilon -A}{\left| q \right|{{U}_{AK}}}}\left( 5 \right)$
| Bài tập 22: Một tụ điện phẳng gồm hai bản A và K rất rộng song song với nhau. Cho công thoát của kim loại dùng làm bản tụ bằng 2,1 eV. Chiếu chùm sáng kích thích rất hẹp có bước sóng bằng 0,4 $\mu m$ (trong chân không) tới một điểm nằm giữa mặt bên trong bản K của tụ điện. Biết hiệu điện thế ${{U}_{AK}}=50$ V. Khoảng giữa hai bản tụ bằng 5 cm. Bán kính khu vực mà êlectron quang điện bắn phá trên bản A của tụ là
A. 1,42 cm. B. 2,84 cm. C. 4,21 cm. D. 8,42 cm. |
Lời giải chi tiết
Bán kính khu vực mà electron quang điện bắn phá trên bản anôt của tụ là
${{R}_{\text{max}}}=2\text{d}\sqrt{\frac{\varepsilon -A}{\left| q \right|{{U}_{AK}}}}=2.0,05\sqrt{\frac{\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{0,{{4.10}^{-6}}}-2,1.1,{{6.10}^{-19}}}{1,{{6.10}^{-19}}.50}}=0,0142m=1,42$ cm. Chọn A.
– Chiếu vào một điểm cố định trên anôt tia sáng có bước sóng $\lambda $:
Sau khi bứt ra khỏi anôt, dưới tác dụng của lực điện electron bị hút ngược trở lại anôt.
Electron đi được xa nhất là electron có vận tốc cực đại và đi theo phương vuông góc với bề mặt anôt. Đi từ $A\Rightarrow K$, động năng bị giảm một lượng: $\Delta {{\text{W}}_{d}}=e{{U}_{AK}}$
Để không có electron nào tới được catôt: $e{{U}_{AK}}>{{\text{W}}_{dm\text{ax}}}=\left( \varepsilon -A \right)\Rightarrow {{U}_{AK}}>\frac{\varepsilon -A}{e}.$
| Bài tập 23: Một tụ điện phẳng gồm hai bản A và K rất rộng song song với nhau. Công thoát của kim loại dùng làm bản tụ bằng 1,5 eV. Chiếu chùm sáng kích thích rất hẹp có bước sóng bằng 0,5 $\mu m$ (trong chân không) tới một điểm nằm giữa mặt bên trong bản A của tụ điện. Để không có electron quang điện nào tới được bản K của tụ điện thì ${{U}_{AK}}$ phải thoả mãn điều kiện là
A. ${{U}_{AK}}<-0,984$ V. B. ${{U}_{AK}}>0,984$ V. C. ${{U}_{AK}}>1,05$ V. D. ${{U}_{AK}}<-1,05$ V. |
Lời giải chi tiết
Để không có electron quang điện nào tới được bản K của tụ điện thì ${{U}_{AK}}$ phải thoả mãn điều kiện là:
${{U}_{AK}}>\frac{\varepsilon -A}{e}\Leftrightarrow {{U}_{AK}}>\frac{\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{0,{{5.10}^{-6}}}-2,4.1,{{6.10}^{-19}}}{1,{{6.10}^{-19}}}=0,984$ V. Chọn B.
a) Chuyển động của electron quang điện trong từ trường đều.
Đặt một bản kim loại phẳng, rộng, trung hoà về điện vào một từ trường đều có đường sức từ song song với bề mặt kim loại và có độ lớn cảm ứng từ bằng B. Chiếu sáng tấm kim loại bằng bức xạ có bước sóng thích hợp làm bứt ra các electron quang điện.
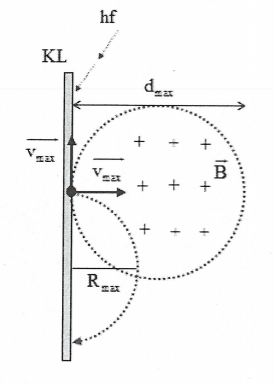
Trong miền từ trường đều $\overrightarrow{B}$, electron quang điện sẽ chịu tác dụng của lực Lorenxơ, lực này đóng vai trò là lực hướng tâm làm cho chúng chuyển động theo quỹ đạo tròn bán kính R:
${{F}_{1}}=evB=m\frac{{{v}^{2}}}{R}\Rightarrow R=\frac{mv}{eB}$
Những electron quang điện phát ra theo hướng song song với bề mặt kim loại thì sẽ rời xa bản kim loại một khoảng lớn nhất:
${{d}_{\text{max}}}=2{{\text{R}}_{\text{max}}}=2\frac{m{{v}_{\text{max}}}}{eB}$
Với ${{v}_{\text{max}}}$ được xác định thông qua công thức Anh-xtanh:
$\varepsilon -A=\frac{1}{2}mv_{om\text{ax}}^{2}\Rightarrow {{v}_{om\text{ax}}}=\sqrt{\frac{2\left( \varepsilon -A \right)}{m}}$
$\Rightarrow {{d}_{\text{max}}}=2\frac{m{{v}_{\text{max}}}}{eB}=\frac{\sqrt{8m\left( \varepsilon -A \right)}}{eB}$.
| Bài tập 24: Phía trước một bản kim loại phẳng, rộng, trung hoà về điện có giới hạn quang điện bằng 0,35 $\mu m$, có một từ trường đều có đường sức song song với bề mặt kim loại và có độ lớn cảm ứng từ bằng 0,5 T. Chiếu sáng tấm kim loại bằng bức xạ có bước sóng 0,15 $\mu m$ (trong chân không). Các electron quang điện có thể rời xa tấm kim loại một khoảng lớn nhất là
A. $29,35\mu m$ B. $15,23\mu m$ C. $27,48\mu m$ D. $4,15\mu m$ |
Lời giải chi tiết
Các electron quang điện có thể rời xa tấm kim loại một khoảng lớn nhất là:
${{d}_{\text{max}}}=2\frac{m{{v}_{\text{max}}}}{eB}=\frac{\sqrt{8m\left( \varepsilon -A \right)}}{eB}=\frac{\sqrt{8m\left( \frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}} \right)}}{eB}$
$=\frac{\sqrt{8.9,{{1.10}^{-31}}.6,{{625.10}^{-34}}{{.3.10}^{8}}\left( \frac{1}{0,{{15.10}^{-6}}}-\frac{1}{0,{{35.10}^{-6}}} \right)}}{1,{{6.10}^{-19}}.0,5}$
$=29,{{35.10}^{-6}}m=29,35\mu m$. Chọn A.
| Bài tập 25: Một tụ điện phẳng gồm hai bản A và K rất rộng song song và cách nhau một khoảng bằng 5 mm. Bản K của tụ điện đang trung hoà về điện có giới hạn quang điện bằng 0,35 $\mu m$. Đặt một từ trường đều có đường sức song song với hai bản tụ và có độ lớn cảm ứng từ bằng 0,25 T. Chiếu sáng bản K của tụ điện bằng bức xạ đơn sắc có bước sóng $\lambda $. Để không có dòng điện chạy qua tụ thì bước sóng của ánh sáng kích thích $\lambda $ phải thoả mãn điều kiện
A. $\lambda <3,{{62.10}^{-11}}$ m. B. $\lambda >3,{{62.10}^{-11}}$ m. C. $\lambda \le 6,2$ pm. D. $\lambda \ge 6,2$ pm. |
Lời giải chi tiết
Để không có dòng điện chạy qua tụ thì electron quang điện bứt ra không đến được A, tức:
${{d}_{\text{max}}}<d\Leftrightarrow {{d}_{\text{max}}}=\frac{\sqrt{8m\left( \varepsilon -A \right)}}{eB}<d\Leftrightarrow \varepsilon <\frac{{{d}^{2}}{{e}^{2}}{{B}^{2}}}{8m}+A$
$\Leftrightarrow \frac{hc}{\lambda }\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{5,{{495.10}^{-15}}}=3,{{62.10}^{-11}}$ m. Chọn B.
